分数阶Laguerre型电报方程的解析解

陈 阳,胡 越

(1.郑州工业应用技术学院基础教学部,河南 新郑 451100;2.河南理工大学数学与信息科学学院,河南 焦作 454000)

分数阶Laguerre型电报方程的解析解

陈 阳,胡 越

(1.郑州工业应用技术学院基础教学部,河南 新郑 451100;2.河南理工大学数学与信息科学学院,河南 焦作 454000)

目的 针对一类特殊的分数阶电报方程——Laguerre型分数阶电报方程,拟通过不同求解方法分析其解的级数形式,为有效解决分数阶微分方程近似解提供便利求解方法。方法 以Laguerre型分数阶电报方程为研究对象,通过同伦摄动、Adomian分解法、变分迭代法、各种积分变换法、算子方法及同伦分析法等研究方法,分析Laguerre型分数阶电报方程解的具体形式。通过深入研究各种方法的优缺点，发现利用算子方法可以构建带初边值条件的时间(空间)分数阶电报方程的解的结构。结果 给出了Laguerre型分数阶电报方程不同初边值形式下的4个定理，分别给出对应形式下解的结构,结合具体定理的运算过程充分证明解的结构的正确性。结论 采用算子方法可以有效求解分数阶Laguerre型电报方程的解析解,且具有准确性高的特点,为此类问题的求解方法提供科学指导。

算子方法;分数阶电报方程;Riemann-Liouville分数阶导数;Caputo分数阶导数

0 引 言

电报方程也称传输线方程,长久以来,一直是数学家和工程师们关注的焦点[1，2]。电报方程可刻画波动和传导两种特性,在数学建模中有广泛应用。近年来,分数阶电报方程[3-6]在理论和应用上都受到了极大关注,有了很大的发展。

目前,分数电报方程已经应用于许多科学领域,用来描述各种现象,如多孔材料的流体流动、反应扩散现象、粘弹性材料中的声波传播、自相似结构动力学、生物电系统中的信号处理等等[8-10]。由于分数阶微积分[11-12]自身的特点,它的引入在一定程度上弥补了古典微分方程在刻划客观现实时的缺陷。

然而,从实际问题归纳出的分数阶电报方程往往是非线性、变系数的偏微分方程。这些问题绝大多数求不出精确的解析解,一般得到的是数值解[13-16],为了求解其解析形式,必须使用近似方法求解。这样的方法很多,各有优缺点。常用的有同伦摄动法(HPM)[17-24]、Adomian分解法[25-28]、变分迭代法(VIM)[29-32]、各种积分变换法[33,34]、算子方法[35，36]等。

本文主要研究下列两类问题:

I.时间分数阶Laguerre型电报方程边值问题(BVP)

(1)

和

(2)

II.空间分数阶Laguerre型电报方程(IVP)

(3)

和

(4)

这里Dα表示Caputo导数,n为正整数,m、c为常数。

在一定条件下,得到方程(1)～(4)的算子形式解析解。

1 预备知识

首先,给出本文中涉及到的几个分数阶导数的定义和性质。详细处可参考文献[11，12]。

定义1.1 如果f∈Cα,α≥-1,称f的μ阶Riemann-Liouville分数积分为

(5)

其中Γ(.)为著名的伽玛函数。

性质1.2 设f(t)=tλ,λ≥0,则有

其中m:=[α]。

证明:当f(t)=tλ时,

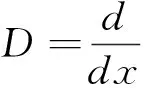
引理1.4 设λ>0,α>0,β>0,当α+β≤λ时,有

Dα+βtλ=DαDβtλ(t>0)

证明:

=Dα+βtλ

D(k+1)αg(t)=DαDkαg(t)

证明:令[α(k+1)]=m,当m-1<α(k+1)≤m时,有

(6)

因为[αk]=[α(k+1)]-1=m-1,可以得到

(7)

把式(7)代入式(6),得

2 结 论

下面介绍本文的主要定理。

定理2.1 设m是一个实或复数,n∈N。在t>0半平面,考虑如下的时间分数Laguerre型电报方程(BVP)

(8)

证明:利用Laguerre导数的谱性质,当n=1时,可以得到

假设n=l时,结论成立,下面考虑n=l+1时的情形。则有

=D(xD+m)l(xD+m)u(x,t)

=D[xD(xD+m)l+m(xD+m)l]u(x,t)

=Dxd(xD+m)lu(x,t)+Dm(xD+m)lu(x,t)

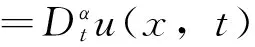
定理2.2 设m是实或复数,n∈N。在x>0半平面,考虑如下的空间分数阶Laguerre型电报方程(IVP)

(9)

(10)

例1 考虑下列时间分数阶电报方程(BVP)

(11)

问题(11)是时间分数阶Laguerre型电报方程(BVP)

(12)

当α=0.5,m=1,n=2,g(t)=t时的特殊情况,由定理3.1,可以得到

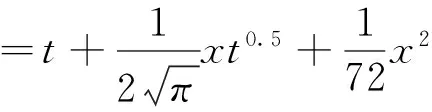
例2 考虑下列空间分数阶电报方程(IVP)

(13)

方程(13)是空间分数阶Laguerre型电报方程(IVP)

(14)

当α=0.4,m=1,n=2,h(x)=x2时的特殊情况。可以得到

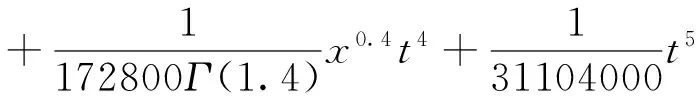
定理2.3 设m是一个实或复数,n∈N。在t>0半平面,考虑如下的时间分数阶Laguerre型电报方程(BVP)

(15)

(16)

证明:首先由引理(6),有

=D(xD+m)u(x,t)

注意到

由谱性质,可得

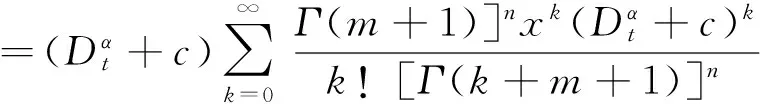
从而定理得证。

定理2.4 设m是一个实或复数,n∈N。在x>0半平面,考虑如下的空间分数阶Laguerre型电报方程(IVP)

(17)

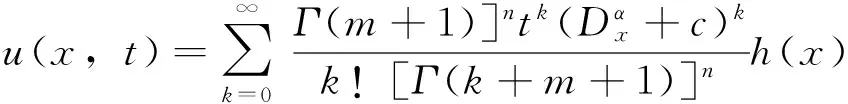
(18)

注记1.在定理1.1.1、定理1.1.2、定理1.1.3和定理1.1.4中,条件[αk]=[α(k+1)]-1是一个充分条件。

通过仔细阅读Roberto Garra的文章[39],发现他在求解空间分数阶Laguerre型电报方程(BVP)的解析解时,给出的结论在一般情况下是错误的。

比如,设g(t)=t,α=0.6,一方面有

另一方面有

又因为

所以

3 结 论

本文考虑了几类含Laguerre型导数的分数阶电报方程的初边值问题,即分数阶Laguerre型电报方程的初边值问题。

当分数阶导数的阶数满足一定的条件时,分数阶导数的半群性质成立,此时结合Laguerre型导数的谱性质,可以使用含分数阶导数算子的形式无穷级数给出这些问题的解析解,称这种技巧为算子方法。

算子方法在求解Laguerre型电报方程的解析解方面是一个有力的武器,它具有计算简单、结构清晰等特点;对分数阶情形,当定理的条件满足时,可以直接给出形式解析解,这对于理论分析和实际应用都是非常方便、有用的。

[1]Cascaval R C,Eckstein E C,Frota C L,et al.Fractional telegraph equations[J].J Math Anal Appl,2002,276(01):145-159.

[2]Orsingher E,Beghin L.Time-fractional telegraph equations and telegraph processes with Brownian time[J].Prob Theory Relat Fields,2004,128(01):141-160.

[3]Momani S.Analytic and approximate solutions of the space-and time-fractional telegraph equations[J].Appl Math Comp,2005,170(02):1126-1134.

[4]Biazar J,Eslami M.Analytic solution for telegraph equation by differential transform method[J].Physics Lett A,2010,374(29):2904-2906.

[5]Chen J,Liu F,Anh V.Analytical solution for the time-fractional telegraph equation by the method of separating variables[J].J Math Anal Appl,2008,338(02):1364-1377.

[6]El-Azab M S,El-Gamel M.A numerical algorithm for the solution of telegraph equations[J].Appl Math Comp,2007,190(01):757-764.

[7]Galue L,Kalla S L,Al-Saqabi B N.Fractional extensions of the temperature field problems in oil strata[J].Appl Math Comp,2007,186(01):35-44.

[8]Mainardi F.The fundamental solutions for the fractional diffusion-wave equation[J].Applied Mathematics Letters,1996,9(06):23-28.

[9]Ghotbi A R,Bararnia H,Domairry G,et al.Investigation of a powerful analytical method into natural convection boundary layer flow[J].Commun Nonlin Sci Numer Simul,2009,14(05):2222-2228.

[10]Li C,Deng W.Remarks on fractional derivatives[J].Appl Math Comp,2007,187(02):777-784.

[11]Zhang J.A Sumudu-based algorithm for solving differential equations[J].Comp Sci J Moldova,2007,15(03):45.

[12]Atangana A,Secer A.A note on fractional order derivatives and table of fractional derivatives of some special functions[J].Abstract Appl Anal,2013：215-222.

[13]Chen C M,Liu F,Turner I,et al.Numerical approximation for a variable-order nonlinear reaction-subdiffusion equation[J].Numer Algor,2013,63(02):265-290.

[14]Chen J,Liu F,Burrage K,et al.Numerical techniques for simulating a fractional mathematical model of epidermal wound healing[J].J Appl Math Comp,2013,41(1-2):33-47.

[15]Zhang X,Liu J,Wen J,et al.Analysis for one-dimensional time-fractional tricomi-type equations by LDG methods[J].Numer Algor,2013,63(01):143-164.

[16]Zhang X,Huang P,Feng X,et al.Finite element method for two-dimensional time-fractional tricomi-type equations[J].Numer Methods Partial Differ Equat,2013,29(04):1081-1096.

[17]Van Dyke M.Perturbation Methods in Fluid Mechanics[M].New York: Academic Press,1964.

[18]He J H.Homotopy perturbation method for bifurcation of nonlinear problems[J].Intern J Nonlin Sci Numer Simul,2005,6(02):207-208.

[19]He J H.The homotopy perturbation method for nonlinear oscillators with discontinuities[J].Appl Math Comp,2004,151(01):287-292.

[20]Liao S.On the homotopy analysis method for nonlinear problems[J].Appl Math Comp,2004,147(02):499-513.

[21]Yildirim A.He’s homotopy perturbation method for solving the space-and time-fractional telegraph equations[J].Intern J Comp Math,2010,87(13):2998-3006.

[22]Khan M,Gondal M A,Hussain I,et al.A new comparative study between homotopy analysis transform method and homotopy perturbation transform method on a semi-infinite domain[J].Math Comp Modell,2012,55(03):1143-1150.

[23]Hashim I,Abdulaziz O,Momani S.Homotopy analysis method for fractional IVPs[J].Commun Nonlin Sci Numer Simul,2009,14(03):674-684.

[24]Jafari M A,Aminataei A.Improved homotopy perturbation method[J].Intern Math Forum,2010,5(32):1567-1579.

[25]Adomian G.A review of the decomposition method in applied mathematics[J].J Math Anal Applic,1988,135(02):501-544.

[26]Daftardar-Gejji V,Jafari H.Adomian decomposition:A tool for solving a system of fractional differential equations[J].J Math Anal Applic,2005,301(02):508-518.

[27]Wazwaz A M.The modified decomposition method for analytic treatment of differential equations[J].Appl Math Comp,2006,173(01):165-176.

[28]Momani S,Shawagfeh N.Decomposition method for solving fractional Riccati differential equations[J].Appl Math Comp,2006,182(02):1083-1092.

[29]Odibat Z M,Momani S.Application of variational iteration method to nonlinear differential equations of fractional order[J].Intern J Nonlin Sci Numer Simul, 2006,7(01):27-34.

[30]He J H.Variational iteration method for autonomous ordinary differential systems[J].Appl Math Comp,2000,114(02):115-123.

[31]He J H.Variational iteration method-a kind of non-linear analytical technique:some examples[J].Intern J Non-lin Mech，1999,34(04):699-708.

[32]He J H.Variational iteration method—some recent results and new interpretations[J].J Comp Appl Math,2007,207(01):3-17.

[33]Kumar S.A new analytical modelling for fractional telegraph equation via Laplace transform[J].Appl Math Modell,2014,38(13):3154-3163.

[34]Kilicman A,Eltayeb H.A note on integral transforms and partial differential equations[J].Appl Math Sci,2010,4(03):109-118.

[35]Luchko Y,Gorenflo R.An operational method for solving fractional differential equations with the Caputo derivatives[J].Acta Math Vietn,1999,24(02):207-233.

[36]Garra R.Analytic solution of a class of fractional differential equations with variable coefficients by operatorial methods[J].Intern J Nonlin Sci Numer Simul,2007,17(2012):1549-1554.

[责任编辑：关金玉 英文编辑：刘彦哲]

Analytical Solutions of Fractional Laguerre Telegraph Equation

CHEN Yang,HU Yue

(1.Department of Basic Courses,Zhengzhou University of Industrial Technology,Xinzheng,Henan 451100,China;2.Institute of Mathematics and Information Science,Henan Polytechnic University,Jiaozuo,Henan 454000,China)

Objective For a special class of fractional telegraph equations—Laguerre type fractional telegraph equation,the solution in the form of a series of different solving methods was discussed to solve approximate solution of fractional differential equations.Methods Using moving homotopy perturbation method,Adomian decomposition method,variational iteration method,various integral transform method,operator method,homotopy analysis method and other research methods to analyze the specific form of the solution Laguerre fractional telegraph equation.By in-depth studying the advantages and disadvantages of each method，the operator method was found to be used to build the structure of the solution time boundary conditions with time-(space-)fractional telegraph equation.Results Four different theorems about initial and boundary Laguerre fractional telegraph equation were given corresponding the form of solutions structure,and proved the solutions structure in combination with the specific process theorems.Conclusions By using the method,operators can effectively solve the analytical solution of Laguerre telegraph equation.So the method has the characteristics of high accuracy and provides scientific guidance to solving such problems.

operator method;fractional telegroph equation;Riemann-Liouville fractional derivative;Caputo fractional derivative

陈阳(1988-)，女,河南焦作人,郑州工业应用技术学院硕士研究生。

胡越，理学硕士，河南理工大学数学与信息学院教授。

O 175

A

10.3969/j.issn.1673-1492.2017.03.005

来稿日期：2016-07-06