四阶上三角矩阵空间的保持伴随矩阵的函数

樊玉环，马艳芬

(黑龙江工程学院数学系，黑龙江 哈尔滨 150001)

四阶上三角矩阵空间的保持伴随矩阵的函数

樊玉环，马艳芬

(黑龙江工程学院数学系，黑龙江 哈尔滨 150001)

目的 保持问题有很多种分类：从保持映射的角度，保持问题通常分为算子代数上的保持问题和矩阵代数上的保持问题；从保持不变量的角度，保持问题一般分为4类，即保持函数、保持变换、保持子集和保持关系；从映射自身角度出发通常将保持问题分为线性保持问题、加法保持问题、乘法保持问题、一般及其他保持问题。建立了四阶上三角矩阵空间的保持伴随矩阵的函数形式。方法 有关保持矩阵一些性质的函数研究，主要从两个方面去研究：一是寻求保持矩阵的不变量，例如有幂等性、正交性、对合、行列式及秩等，二是矩阵空间的改变，有全矩阵空间、对称矩阵空间、反对称矩阵空间及上三角矩阵空间等。运用矩阵代数的知识，寻找各种特殊的四阶上三角矩阵，再利用函数f保持伴随矩阵的条件，不断地得到有关f所满足的各种等式。结果f是四阶上三角矩阵空间的保持伴随矩阵的函数的充要条件是f=f(1)δ，其中f满足f3(1)=f(1)，δ是F域上的单的自同态。结论 四阶上三角矩阵空间上保持伴随矩阵的函数的形式已给出，但任意阶上三角矩阵空间上保持伴随矩阵的函数有待进一步研究。

保持;伴随矩阵;上三角矩阵;函数

各种不变量以及不变量保持的映射和变换历来是数学各学科领域关注的问题，因为这种问题常常有较强的实际背景。在矩阵理论研究中，保持问题已成为一个十分活跃的领域。一方面是因为它有理论价值；另一方面是因为这些问题在微分方程、系统控制、数理统计等领域有着广泛的实际应用背景。关于保持问题的研究,许多学者做了大量的工作，取得了丰富的成果，有关这一领域的研究资料可参看文献[1]～[13]。文献[1]中姚红梅研究了全矩阵空间上的保持伴随矩阵的函数的形式，文献[2]研究了上三角矩阵空间保幂等函数的形式，随后，大量的文章研究了矩阵空间上保持某不变量函数的形式，例如文献[2]～[5]。但关于特殊矩阵空间上保持伴随矩阵函数文章至今还没有，本文描述了四阶上三角矩阵空间保持伴随矩阵函数的形式，任意阶上三角矩阵空间上的保持伴随矩阵的函数的形式有待于进一步研究。

1 符号及基本概念

设F是任意给定的域,F*表示F/{0},T4(F)为F上所有四阶上三角矩阵的全体,A=(aij)，

Af=(f(aij))。

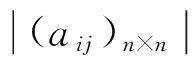
令Aij=(-1)i+jMij，称Aij为元素aij的代数余子式。

定义3[1]若f：F→F满足(A*)f=(Af)*，∀A∈T4(F)，则称函数f：F→F是四阶上三角矩阵空间的保持伴随矩阵的函数。

定义4[15]若f：F→F满足f(a+b)=f(a)+f(b),f(ab)=f(a)f(b)，则称f：F→F是同态。

2 结 论

定理1 f是四阶上三角矩阵空间的保持伴随矩阵的函数的充要条件是f=f(1)δ，其中f满足f3(1)=f(1)，δ是域F上的单的自同态。

证明 先证明充分性

由f=f(1)δ，其中f满足f3(1)=f(1)，δ是域F上的单的自同态。可知f是四阶上三角矩阵空间的保持伴随矩阵的函数，即证明对于任意的A∈T4(F)，有(A*)f=(Af)*。即任意的(i,j)元相等，下面以(2,3)元为例进行证明。

f(b2c3d4) =f(1)δ(b2c3d4)

=f(1)δ(b2)δ(c3)δ(d4)

=f(1)δ(b2)f(1)δ(c3)f(1)δ(d4)

=f(b2)f(c3)f(d4)

同理，f(a1c3d4)=f(a1)f(c3)f(d4)，f(a1b2d4)=f(a1)f(b2)f(d4)，f(a1b2c3)=f(a1)f(b2)f(c3)。

由定义4可知

f(a)=f(a)+f(0)⟹f(0)=0

0=f(0)=f(a)+f(-a)⟹f(-a)=-f(a)

故f(-a2c3d4)=-f(a2c3d4)=-f(a2)f(c3)f(d4)

f(-a1b3d4)=-f(a1)f(b3)f(d4),f(-a1b2c4)=-f(a1)f(b2)f(c4)

f(d4(a2b3-a3b2))=f(d4)f(a2)f(b3)-f(d4)f(a3)f(b2)

f(a1(b3c4-c3b4))=f(a1)f(b3)f(c4)-f(a1)f(c3)f(b4)

f(c3(a2b4-b2a4)+c4(a2b3-a3b2))=f(c3)f(a2)f(b4)-f(c3)f(b2)f(a4)

+f(c4)f(a2)f(b3)-f(c4)f(a3)f(b2)

下面分步骤证明必要性。

步骤1：证明f(0)=0及f3(1)=f(1)。

由伴随矩阵的定义，可得

由(A*)f=(Af)*,可知

f(0)=0

(1)

f3(1)=f(1)

(2)

步骤2：f(-a)=-f(a)。

由伴随矩阵的定义、(1)式及(2)式可得

由(A*)f=(Af)*, 可知

f(-a)=-f(a)f2(1)

由(2)式可知f(1)=0或f2(1)=1。

若f(1)=0， 则f(a)=0， 再由a的任意性， 可知f≡0；

若f2(1)=1， 则f(-a)=-f(a)。

(3)

下面的步骤均在f2(1)=1的情况下证明。

步骤3：f(ab)=f(1)f(a)f(b)。

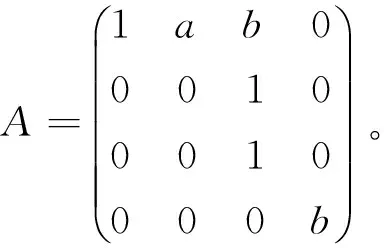
由伴随矩阵的定义及(1)式可得

由(A*)f=(Af)*, 可知

f(ab)=f(1)f(a)f(b)

(4)

步骤4：f(1+x)=f(1)+f(x)。

由伴随矩阵的定义、(1)式、(2)式及(3)式可得

由(A*)f=(Af)*, 可知

f(1+x)=f(1)+f(x)

(5)

步骤5：f=f(1)δ， 其中δ是域F上的单的自同态。

由f2(1)=1及f=f(1)δ，δ=f(1)f

应用(4)式得

δ(ab) =f(1)f(ab)

=f(1)f(1)f(a)f(b)

=δ(a)δ(b)

即得

δ(ab)=δ(a)δ(b)

(6)

应用(2)式、(4)式、(5)式及(6)式得

δ(a+b) =δ(a(1+a-1b))

=δ(a)δ(1+a-1b)

=f(1)f(a)f(1)f(1+a-1b)

=f(1)f(a)f(1)(f(1)+f(a-1b))

=f3(1)f(a)+f2(1)f(a)f(a-1b))

=f(1)f(a)+f(1)f(b)

即得

δ(a+b)=δ(a)+δ(b)

(7)

由f2(1)=1可知，f(1)≠0， 再对∀a∈F*， 有

f(1)=f(aa-1)=f(a)f(a-1)

即

f(a)≠0,∀a∈F*

(8)

若δ(a)=δ(b), 则f(a)=f(b)，f(a)-f(b)=0， 应用(3)式、f(a)+f(-b)=0，f(1)f(a)+f(1)f(-b)=0， 即δ(a)+δ(-b)=0， 应用(7)式δ(a-b)=0，f(1)δ(a-b)=0， 即f(a-b)=0， 应用(8)式得a=b。

从而δ是域F上的单的自同态。

[1]Yao H,Song X,Wang G.A ote on functions preserving some properties of mtrices[A].Huang T Z,Li H B.Proceeding of the Sixth International Conference of Matrices and Operators[C].Chengdu:World Academic Union,2011:77-80.

[2]樊玉环，王佩臣.域上上三角矩阵空间的保持幂等的函数[J].河北科技大学学报,2013,34(03):200-203.

[3]樊玉环，马艳芬，蒋超凡.域上保持对合矩阵的函数[J].河北科技大学学报,2014,35(06):538-542.

[4]樊玉环，马晓峰，谭丽娟.域上特殊矩阵空间的保持正交性的函数[J].黑龙江大学学报：自然科学版，2015,32(01)：54-57.

[5]樊玉环，魏喆，修涛.域上特殊矩阵空间的保持行列式的函数[J].齐齐哈尔大学学报：自然科学版，2016,32(01)：81-83.

[6]张显.交换整环上的上三角矩阵的保幂等的线性算子[J].新疆大学学报，1993,10(02):25-27.

[7]Chan G,Lim M,Tan K.Linear preservers on matrices[J].Linear Algebra Appl,1987,(93):67-72.

[8]Li C,Pierce S.Linear preservers Problems[J].Am Math Mon,2001,108(07):591-605.

[9]曹重光.实数域上有限可除代数矩阵空间保幂等的线性算子[J].数学杂志,1992,12(03):349-353.

[10]曹重光.某些环上矩阵模的保幂等的线性映射[J].黑龙江大学学报：自然科学版,1999,16(01):1-4.

[11]Marcus M.All linear operators leaving the unitary group invariant[J].Duke Math J,1959,26(01):155-163.

[12]Marcus M,Westwick R.Linear maps on skew symmetric matrices:The invariance of elementary symmetric functions[J].Pacific J Math Mon,1960,(10):917-924.

[13]侯晋川,崔建莲.算子代数上线性映射引论[M].北京：科学出版社,2002：20-79.

[14]同济大学数学系.线性代数[M].北京：高等教育出版社，2014：1-60.

[15]华罗庚，万哲先.典型群[M].上海：上海科技出版社，1962：15-92.

[责任编辑：关金玉 英文编辑：刘彦哲]

Function Preserving Adjoint Matrix of Four Order Upper Triangular Matrix Space

FAN Yu-huan,MA Yan-fen

(Department of Mathematics,Heilongjiang Institute of Technology,Harbin,Heilongjiang 150001,China)

Objective There are many kinds of classification in the problem of preserving.From the perspective of preserving the mapping,the problem is usually divided into the preserving problems on operator algebra and matrix algebra.From the perspective of maintaining the invariant,the problem is generally divided into four categories,including preserving the function,transformation,subsets and relationship.From the point of view of mapping,the problem is usually divided into linear preserving problem,additive preserving problem,multiplication preserving problem,general and other preserving problems.The function forms of maintaining the adjoint matrix of the four order upper triangular matrix space were established.Methods Research on keeping some properties of the matrix was mainly from two aspects.One was seeking the invariant of a matrix,such as idempotent,orthogonality,involution,determinant and rank.The other was changing matrix space,including full matrix space,symmetric matrix space,anti symmetric matrix space and upper triangular matrix space,etc.Using matrix algebra,a variety of special four order upper triangular matrix were found,and the functionfwas used to maintain the condition of the adjoint matrix,constantly getting all kinds of equations which were satisfied byf.Resultsfwas a function of preserving adjoint matrix of the four order upper triangular matrix space if and only iff=f(1)δ,wherefsatisfiedf3(1)=f(1) andδwas a single endomorphism in the fieldF.Conclusion The form of the function of preserving the adjoint matrix in the four order upper triangular matrix space is given.However,further research is needed to maintain the function of the adjoint matrix in the space of any order upper triangular matrix.

preservation;adjoint matrix;upper triangular matrix;function

黑龙江省教育厅科学研究项目(12541668)

樊玉环(1981-)，女，黑龙江哈尔滨人，讲师,硕士,主要从事代数矩阵保持的研究。

O 153.3

A

10.3969/j.issn.1673-1492.2017.03.001

来稿日期：2016-05-27