学生为什么不明白『以谁为标准移动小数点』
——『一个数除以小数』观课思考
2017-06-06常立钢
◇ 常立钢
一个数除以小数是小数除法的难点,学生总是在移动小数点时出错,主要表现在学生弄不清楚“以谁为标准移动小数点”。
教学片段一:
师:同学们,通过刚才的学习,现在你们会做一个数除以小数的题了吗?(生:会)真的会了吗?咱们试试吧。
(学生独立完成 2.19÷0.3)
生1:我把2.19和0.3的小数点同时向右移动一位(如图 1)。
生2:我把2.19和0.3的小数点同时向右移动两位(如图 2)。
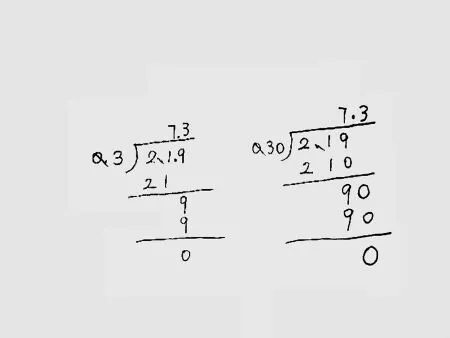
图1
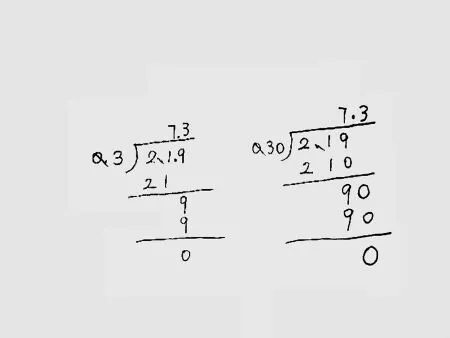
图2
师:对比这两种方法,有什么不同点?
生:一个是以除数为标准进行转化,一个是以被除数为标准进行转化。
师:你赞同哪种方法?
生1:我赞同以除数为标准的,除数扩大10倍的话就变成了整数,这样比较好算。
生2:我认为第二种方法好算,这种方法是以被除数作为标准的,虽然除数变大了,但是被除数变成了整数,这样有利于我们计算。
生3:我也赞同第二种方法,第二种方法好算。
师:谁有疑问?
(老师有些着急了)
生4:我有疑问,如果选择第二种方法,万一除数是三位小数,而被除数是一位小数怎么办呢?
(老师没有抓住难得的机遇)
生5:我觉得这两种方法都可以解决所有的问题,适用哪一种方法就用哪种方法,像2.19÷0.3就比较适用第二种方法。
(刚有好兆头,却转瞬即逝)
师:还有没有不同的意见?
(老师真的着急了)
生6:我觉得归根到底都应该以小数位数多的为标准。假如被除数是两位小数,除数是三位小数,就以除数为标准;如果除数是一位小数,而被除数是三位小数,就以被除数为标准。
(此时老师已经变得非常急躁,马上要下课了)
从以上片段可以看出,经过例题的学习,在巩固练习环节学生还不清楚 “以谁为标准移动小数点”,给他们印象更深的是“要利用商不变的性质”“要移动小数点”“要变成整数”,至于“先把谁变成整数”“以谁为标准移动小数点”,更多的人仍然茫然,甚至有学生干脆把被除数和除数的小数点直接去掉全变成整数来算。为什么学生不清楚“以谁为标准移动小数点”呢?我们先看本课开始时的教学片段。
教学片段二:
师:同学们,你们还记得以前我们学习过的商不变的性质吗?
(师领着学生复习,略)
师:(出示情境图)从图中你获得了哪些数学信息?根据这些数学信息你能提出什么数学问题?怎么列式?
(生答略)
师:我们来观察这个算式,和以前学习的小数除法有什么不同?对,这道题的除数是小数,这节课我们就来共同学习“一个数除以小数”。(板书课题)
师:除数是小数我们不会算,你能用以前的知识算出得数吗?请你尝试着用以前的方法来做一做,开始吧!
从以上片段可以看出,老师先领着学生复习“商不变的性质”,然后明确告诉学生“今天学习的小数除法和以前学习的不同”,并且指出“这种除法我们不会算”,同时提醒学生“能不能用以前的知识来解决”。在这样的引领下,聪明的学生一下子就领会了老师的“意图”,他们已经明白肯定不能再按照“除数是整数”的算法来算了,必须按照以前其他知识来算。于是,一部分学生很快就想到商不变的性质。
这种教学手段看似学生学得很快,但是,学生并没有亲身体验按“除数是小数”来算为什么不行,只是一看到“除数是小数”,就听到老师说“不行”,也没有真正尝试一下遇到的困难。这样的话,就算学生很快学会了“转化”,但这种“转化”是被动的,是老师硬塞给的,在后续的练习中,学生不明白“以谁为标准”就很容易理解了。
实际上,如果没有“商不变性质”的铺垫,学生第一次遇到除数是小数笔算的时候会有何反应呢?我们选取五年级一个班提前试做“8.65÷0.5”,结果如下:
全班31人的试做情况可以分为四类。A类21人(约66.7%),这类学生表示“除数怎么会是小数?不知道如何算”,他们算的得数是0.173、1.73等(如图3)。B类3人(约 9.7%),有 1人仍然按照除数是整数的方法,先拿8除以0.5,再拿0.6除以0.5,一位一位往下除,最后竟然算出了得数17.3,有2人也是按照除数是整数的方法,“硬”往下算,但是没算出来(如图4)。C类3人(约9.7%),也算出了正确得数,但访谈时说“只管除,想着应该这样点小数点,不清楚对不对”。D类4人(约12.9%),这类学生发现除数是小数后,竟然想到了“转化”,最后算出了正确答案“17.3”(如图 5)。

图3

图4

图5
可以看出,大部分学生独立面对一个数除以小数的题目时,受思维定式的影响,先想到的仍是刚刚学过的“除数是整数”的方法,可是一试算,发现“不能除了”。这种亲身体验对学生将除数是小数转化为除数是整数非常有用,因为,只有学生先发现问题,才有可能自发地、主动地想办法解决问题,否则,有些教学只能顾及上面的D类学生,而大部分学生学得比较被动。
因此,如果教学中先让学生独立试算,通过展示以上A、B、C三类学生的作品,引导A类学生说出“不知道如何算”的疑惑,引导B类学生说出“用0.5直接去除太麻烦”的体验,引导C类学生说出“不确定得17.3对不对”的困惑。在此基础上,带领学生回顾商不变的性质,启发学生思考“既然除数是小数不好除”,能不能“将这个小数变成整数”呢?从而引导学生以四人小组为单位开展探究活动。
这样的教学,学生有亲身体验,能发现问题,有对问题解决的探索,就很容易明白“以谁为标准移动小数点”了。
