高中物理匀变速直线运动问题的求解方法
2017-06-05山东省泰安第一中学2015级2班271000
山东省泰安第一中学2015级2班(271000)
张婧茹●
高中物理匀变速直线运动问题的求解方法
山东省泰安第一中学2015级2班(271000)
张婧茹●
匀变速直线运动问题的解法众多,涵盖了公式法、逆推法、求差法、均值法和图像法等等.解题时要根据具体的问题来选择合适的求解方法,否则就会出错误.
匀变速直线运动;解题方法
作为高中物理中常见的一种类型题,匀变速直线运动问题的题型灵活多变,求解方法也各不相同,具体需要针对具体的问题来选择合适的求解方法,但是需要注意的是要始终基于匀变速直线运动的常见模型来选择找寻解题突破口,明确求解方案,确保问题求解的准确度和效率.本文基于匀变速直线运动问题,探讨了其常见的求解方法.
一、公式法
顾名思义,公式法就是在借助位移公式和速度公式等相关运动学公式及基本规律来达到求解物理问题的目的,但是考虑到位移和速度等相关物理量均为矢量,除了具有数值大小之外,同样需要考虑其具体的方向,否则很容易引发解题错误.另外,在采用公式法来求解问题的时候,不可一味地套用公式,避免因盲目的公式套用影响解题准确度,比如“追击”或者“刹车”等均是需要加以注意的类型题.
例1 已知某车辆在刹车前的速度为20m/s,刹车时候的加速度为1m/s2,试求该车辆在刹车25s后的滑行距离?
解析 该道题是一道典型的直线运动问题,其中涉及到初始速度、刹车加速度等参数,只需要套用运动学公式即可求解,但是需要注意的是要确定25s内该车辆的实际运动情况,即是否一直处于匀减速状态,待确定后即可快速解决.
解 由题意可知,该车辆从刹车到停下所需时间t=(0-20)/-1=20s,可知在25s时候车辆已经停止,所以只需套用运动学公式即可求得实际的刹车距离s=v0t-1/2at2=200m.
二、求差法
在高中物理运动学中存在一些涉及到位移差或者时间差的问题,此时可以借助这些位移差或者时间差来辅助运动方程求解,或者可以借此来直接求解出问题的答案,这实际上就是求差法的具体应用原理.
例2 已知某长度为15m的竖杆悬挂在空中,在距离杆下端5m位置处设置有某观察点A,求竖杆全部通过A点所需耗费的时间?(g=10 m/s2)

三、平均法
所谓的平均法主要是借助平均值来达到明确解题思路的目的,具体主要包括平均速度法和中间时刻速读法.实际上,针对匀变速直线运动而言,某段时间范围内运动的平均速度=中间时刻的瞬时速度=1/2×(初始速度+末尾速度),实际的解题过程中可以充分利用该结论来进行问题求解,往往可以收到意想不到的解题效果.
例3 已知某物体做匀加速直线运动,其在第2s内的位移数值为6m,第3s末的速度值为10.5m/s,试求该物体在4s内的位移值?
解析 通过对已知题干信息进行分析可知,该物体在第1.5s时刻的瞬时速度v1.5等于该物体在2s内的平均速度,此时借助两个瞬时时间和速度可以求得相应物体的加速度为4 m/s2,进而可以求得第2s末的瞬时速度v2=7m/s,且其恰好为第4s的平均速度,此时可求出第4s的位移值s=vt=28m.
四、逆推法
通常而言,我们在求解物理问题的过程中常常偏向于采用正向思维来进行求解,但是也有许多物理问题无法采用正向思维来求解,或者说采用正向思维会遇到诸多困难,此时如果可以采用逆向思维法,那么往往可以达到“柳暗花明又一村”的效果.比如,某些匀减速直线运动可以看作是反向的匀加速直线运动,这样可以达到快速求解相关问题的目的.
例5 已知某物体以1 m/s2的加速度做匀减速直线运动直至停止,试求该物体在停止前第4s内的位移?
解析 如果按照常规的匀减速直线运动问题的求解思路进行求解,那么不知道初始运动速度,未知参数比较多,此时如果可以采用逆推法,从逆向考虑,将问题看作是初始速度为0,加速度为1 m/s2的匀加速直线运动,那么可以便捷求出第4s内位移值.
解 先求出第1s的位移值s1=1/2at2=0.5m,接着再运用连续相等时间内位移之比等于连续奇数之比可得s4=7s1=3.5m.
五、图象法
所谓的图象法实际上就是借助图形来直观地展示相关物理问题的具体含义所在,这样可以增强物理问题的直观性和形象性.实际上,在直线运动中,v-t图象和s-t图象均是比较常见的基本图像,其代表图象的截距、斜率、以及图线和t轴所谓面积均具有其特有的物理意义,此时可以充分利用几何方面的数学知识来求解相关的运动学物理问题,从而可以极大地增强问题求解的直观性,降低求解难度.
例6 已知质点从A点沿直线运动到B点后保持静止,期间质点可能做匀速运动或者匀变速运动,试求质点到B点所需的最短时间,已知A点和B点相距s,加速度大小为a.

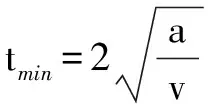
综上所述,匀变速直线运动问题的求解方法众多,涵盖了公式法、逆推法、求差法、均值法和图象法等等,但是为了确保问题求解的准确度,必须要结合具体的题目类型及其考察点来选用合适的求解法,以便可以快速达到求解问题的目的,尤其是要注意切不可照搬公式,否则很容易出现求解误差,影响解题准确度.
G632
B
1008-0333(2017)15-0046-01
