分类讨论思想研究提高解题能力

江苏省常熟市尚湖高级中学(215500)

陆志峰●



分类讨论思想研究提高解题能力

江苏省常熟市尚湖高级中学(215500)

陆志峰●

本文叙述了分类讨论的由来；分类讨论的依据；分类的原则；简化和避免分类讨论的优化策略.本文第二部分和第三部分通过实践说明分类讨论思想在实践中的应用.

不等式；数列；直线方程；抛物线；焦点弦

一、分类讨论思想认知

1.分类讨论是一种逻辑方法，在中学数学中有着极广泛的应用.根据不同标准可以有不同的分类方法，但分类必须从同一标准出发，做到不重复、不遗漏，包括各种情况，同时要有利于问题研究.

2.引导分类讨论的原因大致可归纳为以下几种：

(1)涉及的数学概念是分类讨论的如绝对值|a|的定义：分a>0,a=0,a<0三种情况.这种分类讨论题型可以称为概念型.

(2)运用的数学定理、公式或运算性质、法则是分类给出的，如等比数列的前n项和的公式，分q=1和q≠1两种情况，这种分类讨论题型可以称为性质型.

(3)求解的数学问题的结论有多种情况或多种可能性.如排列、组合、概率中较常见.

(4)数学问题中含有参变量，这些参变量的不同取值导致不同的结果.如解不等式ax>2时，分a>0，a=0和a<0三咱情况讨论，这称为含参型.

(5)较复杂或非常规的数学问题，需要采取分类讨论的解题策略来解决的.

3.分类讨论就是依据一定的标准，对问题分类、求解，要特别注意分类必须满足互斥、无漏、最简的原则，分类讨论常见的依据是：

(1)由概念内涵分类，如绝对值、直线的斜率、指数对数函数、直线与平面的夹角等定义包含了分类.

(2)由公式条件分类，如等比数列的前n项和公式、极限的计算、圆锥曲线的统一定义中图形的分类等.

(3)由实际意义分类，如排列、组合、概率中较常见，但不明显，有些应用问题也需分类讨论.

4.分类原则

(1)对所讨论的全域分类要“即不重复，也不遗漏”；

(2)在同一次讨论中只能按所确定的一个标准进行；

(3)对多级讨论，应逐级进行，不能越级.

5.简化和避免分类讨论的优化策略

(1)直接回避，如运用瓜下法、求补法、消参法等方法有时可以避开烦琐的讨论；

(2)变更主元，如分离参数、变参置换，构造以讨论对象为变量的函数形式解题时可避开讨论；

(3)合理运算，如利用函数奇偶性、变量的对称轮换以及公式的合理选用等有时间可以简化甚至避开讨论；

(4)数形结合，利用函数图象、几何图形的直观性和对称特点有时可以简化甚至避开讨论.

在学习中也要注意优化策略，有时利用转化策略，如反证法、补集法、变更多元法、数形结合法等简化甚至避开讨论.

二、分类讨论思想实践典例

题型：分类讨论问题在不等式中的应用

例题1 解关于x的不等式：ax2-(a+1)x+1<0.

解 (1)当a=0时，原不等式化为-x+1<0

∴x>1.

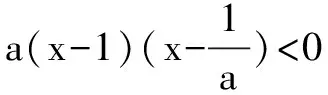
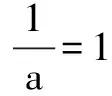
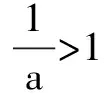
点评 这是一个含参数a的不等式，一定是一元二次不等式吗？不一定，故首先对二次项系数a分类：

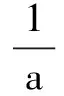
题型：分类讨论问题在数列中的应用

例题2 已知数列{an}满足a1=0,a2=2,且对任意m、n∈N*都有a2m-1+a2n-1=2am+n-1+2(m-n)2.(1)求a3,a4;(2)设bn=a2n+1-a2n-1(n∈N*),证明：{bn}是等差数列；(3)设cn=(an+1-an)qn-1(q≠0,n∈N*),求数列{cn}的前n项和Sn.

解 (1)由题意，令m=2，n=1，可得a3=2a2-a1+2=6;再令m=3,n=1，可得a5=2a3-a1+8=20.

(2)当n∈N*时，由已知(以n+2代替m)可得：a2n+3+a2n-1=2a2n+1+8.

于是[a2(n+1)+1-a2(n+1)-1]-(a2n+1-a2n-1)=8,即bn+1-bn=8,所以{bn}是公差为8的等差数列.

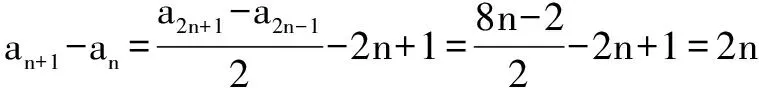
当q=1时，Sn=2+4+6+…+2n=n(n+1).当q≠1时，Sn=2·q0+4·q1+6·q2+…+2n·qn-1.两边同乘以q,可得qSn=2·q1+4·q2+6·q3+…+2n·qn.

点评 等比数列的求和公式只适合于q≠1，特别是公比q中含参数时，需要分类讨论.

三、分类讨论思想应用讨论

题型：巧设直线方程避免分类讨论

在解决抛物线y2=2px(p>0)焦点弦问题时，常用点斜式设焦点弦方程，但此时，要考虑斜率k存在与不存在两种情况.如果我们巧妙的设其方程为：x=my+p/2或x=ycotθ+p/2(θ为焦点弦的倾斜角，0°<θ<180°)就可避免分类讨论的麻烦.

例题3 设抛物线y2=2px(p>0)的焦点为F，经过点F的直线交抛物线于A、B两点，点C在抛物线的准线上，且BC∥x轴，证明直线AC经过原点O.

分析 常规解法是按k不存在设方程为x=p/2，k存在设方程为y=k(x-p/2)，分别求解，比较繁琐.

为避免分类讨论，可设AB的方程为x=my+p/2，A、B的坐标分别为(xA,yA),(xB,yB).将AB方程代入抛物线方程y2=2px，得y2-2pmy-p2=0.由韦达定理得yAyB=-p2,即yB=-p2/y.由于BC∥x轴且C在准线x=-p/2上，故C(-p/2,yB).

例题4 过抛物线y2=2px的焦点作倾斜角为θ的直线交抛物线于A、B两点，设△AOB的面积为S(O为原点)，试用θ、p表示S，并求出S的最小值.

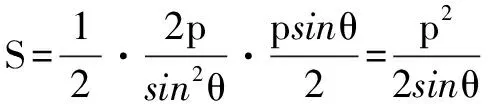
当θ=90°时，S有最小值p2/2，此时焦点弦AB是抛物线的通径.

可见，我们在解决抛物线焦点弦问题时，如果巧妙的设焦点弦方程，将避免分类讨论的麻烦，给我们解题带来许多方便之处.

G632

B

1008-0333(2017)15-0006-02