The Generalization on Inequalities of Hermite-Hadamard’s Integration

LIAN Tie-yan,TANG Wei

(1.College of Bioresources Chemical and Materials Engineering,Shaanxi University of Science and Technology,Xi’an 710021,China;2.College of Electrical and Information Engineering,Shaanxi University of Science and Technology,Xi’an 710021,China)

The Generalization on Inequalities of Hermite-Hadamard’s Integration

LIAN Tie-yan1,TANG Wei2

(1.College of Bioresources Chemical and Materials Engineering,Shaanxi University of Science and Technology,Xi’an 710021,China;2.College of Electrical and Information Engineering,Shaanxi University of Science and Technology,Xi’an 710021,China)

Some new inequalities of Hermite-Hadamard’s integration are established.As for as inequalities about the righthand side of the classical Hermite-Hadamard’s integral inequality refined by S Qaisar in[3],a new upper bound is given.Under special conditions, the bound is smaller than that in[3].

Hermite-Hadamard’s integral inequality;convex function;the H¨older’s integral inequality;third derivative

§1.Introduction

It is common knowledge in mathematical analysis that a function f:I⊂R→R is said to be convex on an interval I if the inequality

is valid for all x,y∈I and λ∈[0,1].

Many inequalities have been established for convex functions but the most famous is the Hermite-Hadamard’s integral inequality,due to its rich geometrical significance and applications,which is stated as follow[1].

If f:I⊂R→R is a convex function on I and a,b∈I with a＜b,then the double inequalities

hold.

A function f:[a,b]⊂R→R is called a quasi-convex on[a,b],if f(λx+(1-λ)y)≤sup{f(x),f(y)}for all x,y∈[a,b]and λ∈[0,1].

Since its discovery in 1893,Hermite-Hadamard’s integral inequality has been considered the most useful inequality in mathematical analysis.In[2],D A Ion discussed inequalities of the right-hand side of the Hermite-Hadamard’s integral inequality for functions whose derivatives in absolute values are quasi-convex functions.

Theorem 1.1[2,Theorems1and2]Assume that a,b∈R with a＜b,f is differentiable function on(a,b)and f′∈L[a,b].

(1)If|f′|is quasi-convex on[a,b],then

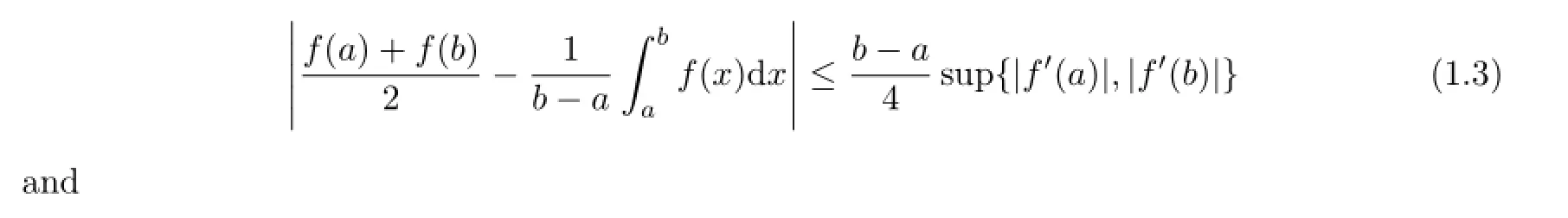
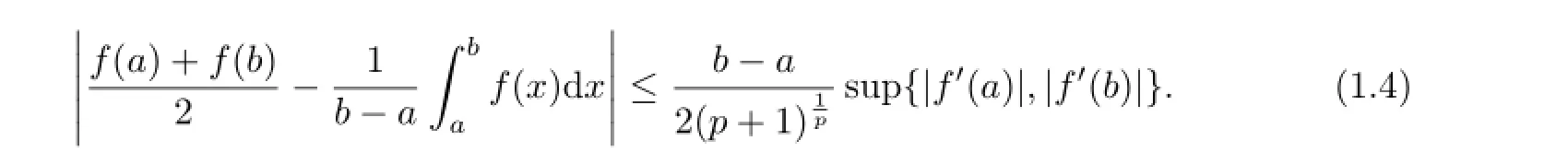
In[3],S Qaisar refined the above inequalities for functions whose third derivatives in absolute values at certain power are quasi-convex functions.

Theorem 1.2[3,Theorems2.2,2.3and2.4]Let f:I⊂R→R be differentiable on I such that f′′′∈L[a,b],where a,b∈I with a＜b.

(1)If|f′′′|is a quasi-convex function on[a,b]and p＞1,then

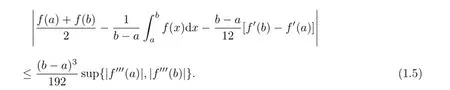
For more results on Hermite-Hadamard’s integral inequality providing new proofs,noteworthy extensions,generalizations and numerous applications,see[1-11]and the references therein.

In this paper,we will create some new integral inequalities of Hermite-Hadamard type for functions whose third derivatives are convex.

§2.Proof Different from the Literature[2]

For establishing some new integral inequalities of Hermite-Hadamard type for functions whose third derivatives are convex,we need an integral identity below.

Lemma 2.1[3]Let f:I⊂R→R be differentiable on I such that f′′′∈L[a,b],where a,b∈I with a＜b,then

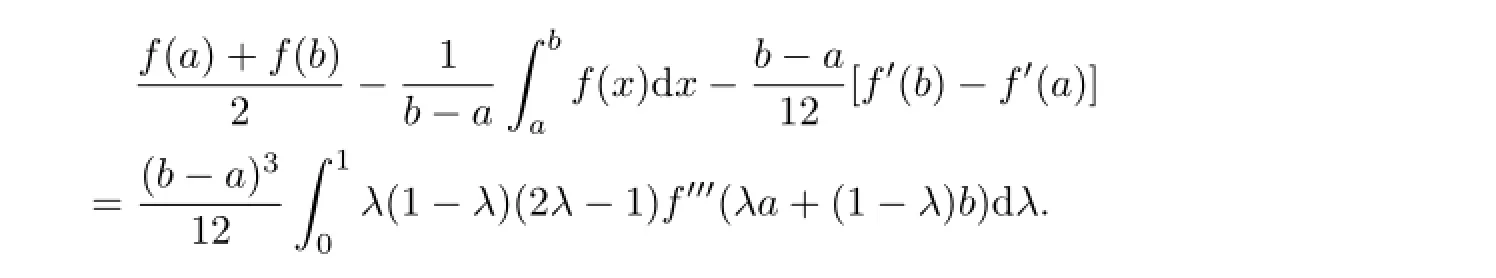
Since|f′′′|qis convex on[a,b],we have

Then by using the facts

The proof is completed.

Theorem 2.2Let f:I⊂R→R be differentiable on I such that f′′′∈L[a,b],where a,b∈I with a＜b.If|f′′′|qis a quasi-convex function on[a,b]and q＞1,then

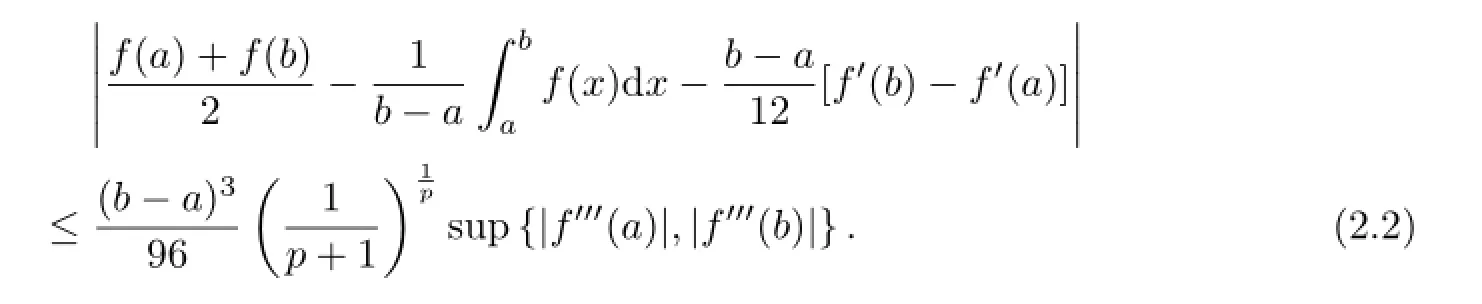
Since|f′′′|qis quasi-convex on[a,b],we have

Then by using the fact

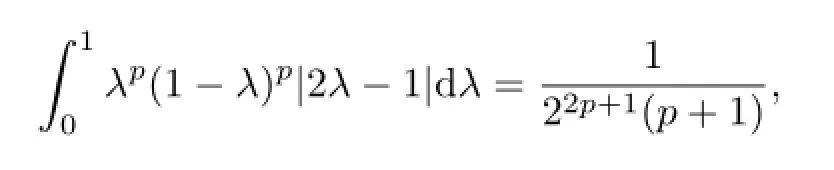
we get

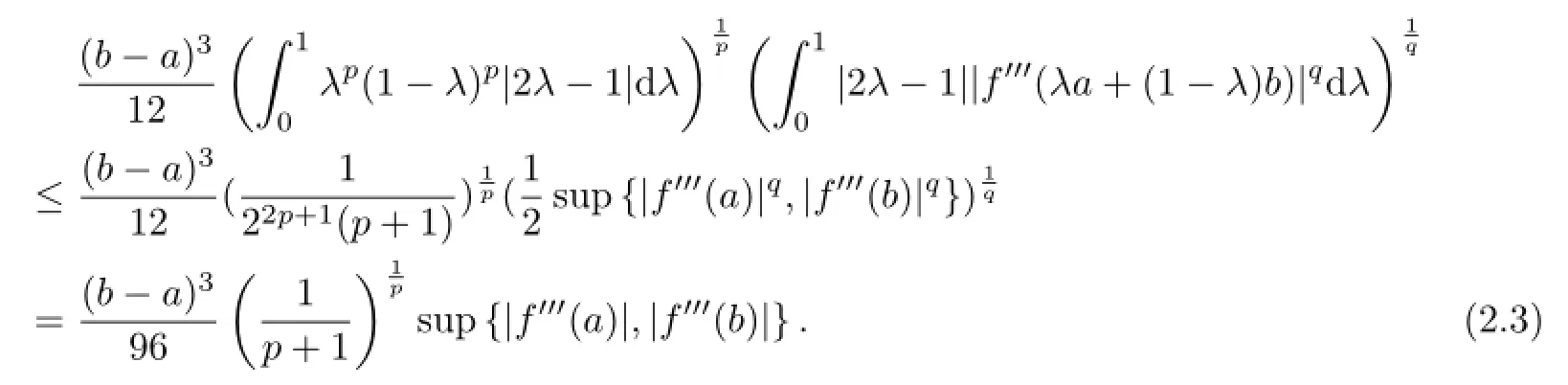
The proof is completed.

(3)燃料型氮氧化合物。此种氮氧化合物由燃料中的氮化合物在燃烧中氧化而成，由于燃料中氮的热分解温度低于粉煤燃烧的温度，600～800 ℃时就会生成燃料型氮氧化合物，其在煤粉燃烧中NOx产物中占60%～80%。在生成燃料型NOx过程中，首先是含有氮的有机化合物热裂解产生N、CN、HCN等中间产物基团。然后再氧化成为NOx。由于煤在燃烧过程中包含挥发分和焦炭燃烧两个部分，故燃料型的氮氧化合物形成也由气相氮的氧化(挥发分)形成和焦炭燃烧形成两个部分组成(图1)。

Remark 2.1It’s clear that inequality(2.2)is equivalent to inequality(1.6).

§3.Some New Hermite-Hadamard Type’s Integral Inequalities

Theorem 3.1Let f:I⊂R→R be differentiable on I such that f′′′∈L[a,b],where a,b∈I with a＜b.If|f′′′|qis a convex function on[a,b]and q≥1,then

ProofFirst of all,we can prove that the two integral identities(3.2)and(3.3)hold.

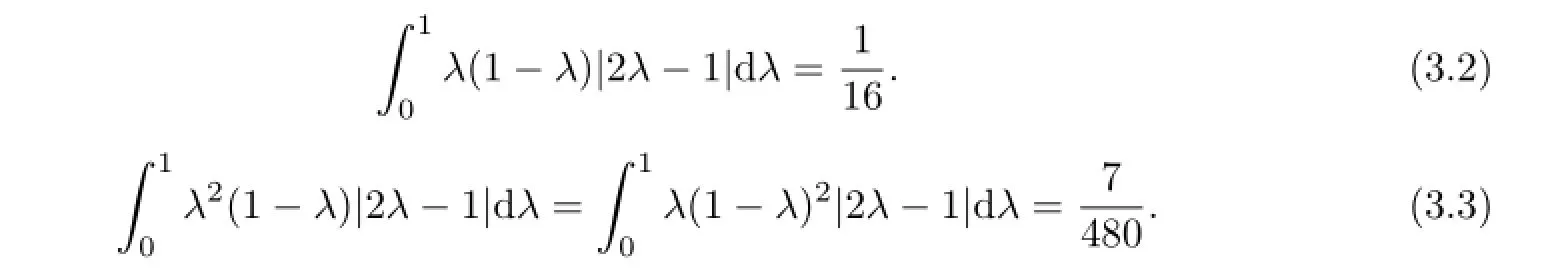
If q=1,by using Lemma 2.1,|f′′|’s convexity on[a,b]and identity(3.3),we have

Since|f′′′|qis convex on[a,b],then

Utilizing the inequalities(3.2)～(3.3),(3.5)～(3.6),we get(3.1).

Corollary 3.1Suppose all the conditions of Theorem 3.1 are satisfied.Then

Theorem 3.2Let f:I⊂R→R be differentiable on I,such that f′′′∈L[a,b],where a,b∈I with a＜b.If|f′′′|is a convex function on[a,b],then for n∈N,the following inequality holds:

ProofBy using Lemma 2.1 and well known the H¨older’s integral inequality,we have

Since|f′′|is a convex function on[a,b],it is easy to prove that|f′′|2nis also a convex function on[a,b].Then we have

Then by using the fact Z1

we get

The proof is completed.

In the case that a quasi-convex function is also a convex function,we can do the following comparison.

Remark 3.1The bound of inequality(3.4)is smaller than that’s of inequality(1.5),the bound of inequality(3.1)is smaller than that’s of inequality(1.6)and(1.7),so the results in [3]are generalized.

§4.Application to Some Special Means

Now,we consider the applications of our Theorems to the special means.

Using the result of Theorem 3.1,we have the following theorem.

Theorem 4.1For positive number a,b such that a＜b with α≥1 and q≥1,we have

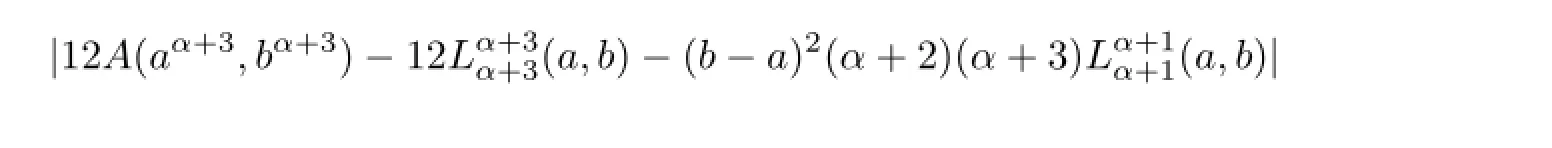
AcknowledgementsThe author is grateful to the anonymous referees for their helpful comments and suggestions.

[2]ION D A.Some estimates on the Hermite-Hadamard inequality through quasi-convex functions[J].Ann Univ Craiova Math Comp Sci Ser,2007,(34):82-87.

[3]QAISAR S,HUSSAIN S,HE C J.On new inequalities of Hermite-Hadamard type for functions whose third derivative absolute values are quai-convex with applications[J].Journal of the Egyptian Mathematical Societly,2014,22(1):19-22.

[4]DRAGMOMIR S S,FITZPATRICK S.The Hadamard inequality for s-convex functions in the second sense[J].Demonstratio Math,1999,32(4):687-696.

[5]DRAGMOMIR S S,AGARWAL R P.Two inequalities for differentiable mappings and applications to special means of real numbers and to trapezoidal formula[J].Appl Math Lett,1998,11(5):91-95.

[6]KIRMACI U S,KLARICIC B K,DEMIR M E,et al.Hadamard-type inequalities for s-convex functions[J]. Appl Math Comput,2007,193(1):26-35.

[7]KIRMACI U S,DEMIR M E.On some inequalities for differentiable mappings and applications to special means of real numbers and to midpoint formula[J].Appl Math Comput,2004,153(1):361-368.

[8]KIRMACI U S.Inequalities for differentiable mappings and applications to special means of real numbers and to midpoint formula[J].Appl Math Comp,2004,147(1):137-146.

[9]LATIF M A,DRAGOMIR S S.New inequalities of Hermite-Hadamard type for functions whose derivatives in absolute value are convex with applications[J].Acta Universitatis Matthiae Belii Series Mathematics, 2013,145(1):24-39.

[10]QAISAR S,HUSSAIN S,HE C J.On new inequalities of Hermite-Hadamard type for functions whose third derivative absolute values are quasi-convex with applications[J].Journal of the Egyptian Mathematical Societly,2014,22(1):19-22.

[11]HUANG Li-ping.The improvement of Fischer’s inequality and Hadamard’s inequality[J].Chin Quart J of Math,1994,9(3):13-18.

tion:47A63

:A

1002–0462(2017)01–0034–08

date:2015-09-24

Supported by the Key Scientific and Technological Innovation Team Project in Shaanxi Province(2014KCT-15)

Biography:LIAN Tie-yan(1978-),female,native of Weinan,Shaanxi,a lecturer of Shaanxi University of Science and Technology,M.S.D.,engages in operator theory.

CLC number:O177.1