Bloch Constant on α-Bloch Mappings of the Unit Ball

XU Qing,LIU Zhi-bin,WANG Jian-fei

(Department of Mathematics and Physics,Information Engineering,Zhejiang Normal University,Jinhua 321004,China)

Bloch Constant on α-Bloch Mappings of the Unit Ball

XU Qing,LIU Zhi-bin,WANG Jian-fei

(Department of Mathematics and Physics,Information Engineering,Zhejiang Normal University,Jinhua 321004,China)

This note is denoted to establishing sharp distortion theorems for subclasses of α-Bloch mappings defined in the unit ball of Cnwith critical points.Furthermore,the estimates of Bloch constant with respect to these subclasses are given.

α-Bloch mappings;distortion theorem;Bloch theorem;Bloch constant

§1.Introduction

In complex analysis,the Bloch theorem due to Bloch[1]in 1925 states that iffis a holomorphic on the unit disk D with f′(0)=1,then there exists an absolute constant r＞0 such that some open subset of U⊂D is mapped biholomorphically by f onto some disk with radius r.

The greatest lower bound of the above r is called Bloch constant.Since de Branges solved the Bieberbach conjecture,finding the exact value of the Bloch constant may be the most important problem in geometric function theory of one complex variable.Though the precise value of the Bloch constant is still unknown,many scholars have obtained some estimates of Bloch constant,for example[3,9,11].

In the case of several complex variables,however,Wu[14]shows that the Bloch theorem fails unless we put some restrictive assumption on holomorphic mappings.Therefore,if thereexists a positive Bloch constant,then we must restrict the class of holomorphic mappings in higher dimensions.More research with respect to Bloch theorems in high dimensions can be referred to[2,5-7,10,12-15].Because α-Bloch mappings generalizes Bloch mappings in higher dimensions,it is natural to consider the Bloch constant estimates for α-Bloch mappings spaces of several complex variables.

This note,we shall establish distortion theorems for many subfamilies of α-Bloch mappings on the unit ball.These classes pay attention to the finite order to which the Jacobian determinant must vanish,as well as for the limiting case of locally biholomorphic mappings.As applications,the estimates of Bloch constants for these subfamilies are obtained.These results enable us to generalize some well-known distortion theorems and Bloch constant estimates from one complex variable to several variables.

For n∈Z+={1,2,3,···}let

be the open unit ball and the unit sphere in the complex n-space Cnrespectively.In general, Bn(x,r)represents the ball of radius r with the center x.Denote H(Bn)by the set of all holomorphic mappings from Bnto Cn.For f∈H(Bn),f is written as follows

where fiis a holomorphic function from Bnto C.The derivative of the mapping f at a point a∈Bnis the complex Jacobian matrix given by

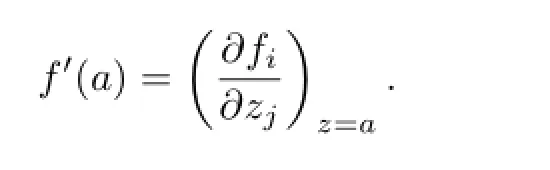
Then f′(a)is a linear mapping from Cnto Cn.Let‖f′(a)‖Mbe the norm of complex Jacobian matrix f′(a).

A holomorphic mapping f∈H(Bn)is called locally biholomorphic if det f′(z)/=0 for every z∈Bn.A point z0is called a critical point offif det f′(z0)=0(in one complex variable,such a point is called a branch point).

Definition 1[4]Let α＞0.A holomorphic mapping f defined on the unit ball Bnis called an α-Bloch mapping if the α-Bloch semiform

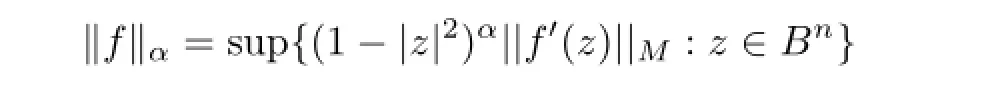
is finite.In particular,when n=1 and α=1,the function f reduces to the classical Bloch function on the unit disk D.

Definition 2[4]Let f∈H(Bn)and α＞0.A functional on f is defined by

Definition 3For any positive integer k,we introduce Hk(Bn)as follows

It is easy to see H1(Bn)=H(Bn)and Hk+1(Bn)⊂Hk(Bn).Let Hloc(Bn)be the class of locally biholomorphic mappings from Bnto Cn.Then Hloc(Bn)⊂Hk(Bn).

This paper,we are interested in the following subfamilies of H(Bn)

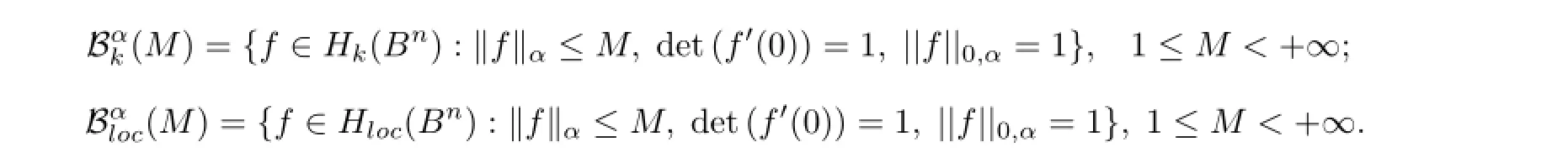
For a holomorphic mapping f∈H(Bn),let r(a,f)be the radius of the biggest univalent ball offcentered at f(a)(a univalent ball Bn(f(a),r)⊂f(Bn)means that f maps an open subset of Bncontaining the point a biholomorphically onto this ball).Let r(f)=sup{r(a,f):a∈Bn}.

Let Bk,α(M)denote the Bloch constant of the family Bαk(M),i.e.,

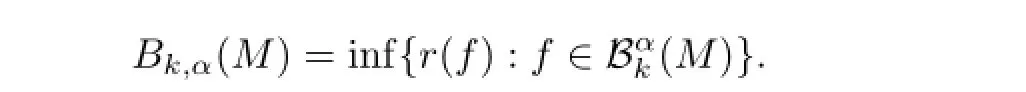
Similarly,let Bloc,α(M)denote the Bloch constant of the family Bαloc(M),i.e.,

§2.Some Lemmas

In order to prove the main results,we need the following three lemmas.

Lemma 1[9]Let f be a holomorphic function on D S{1}.f(D)⊂D,f(1)=1 and all zeros of f(z)have multiplicities at least k.If f′(1)=k,then

(1)|f(x)|≥xkfor x∈[0,1),with equality for some x if and only if f(x)=xk;

Lemma 2[8]Suppose that A=(aij)is an n×n complex matrix.If‖A‖M＞0,then for any unit vector ξ∈∂Bn,the following inequality holds

Lemma 3If f∈H(Bn),‖f‖0,α=1 and det(f′(0))=1,then

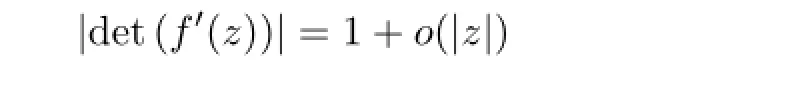
and

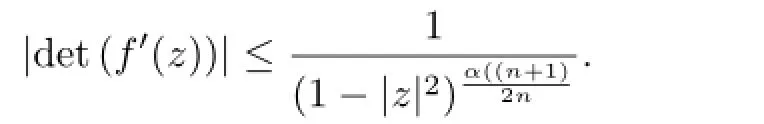
Proof Since‖f‖0,α=1,it means that

Note that det(f′(0))=1,then the above inequality implies that

§3.Main Results

The following Theorem 3.1 extends Bonk Distortion Theorem of the Bloch function of the unit disk to α-Bloch mappings defined in the unit ball of Cn.

Theorem 1 If f∈Hk(Bn),‖f‖0,α=1 and det f′(0)=1,then (a)

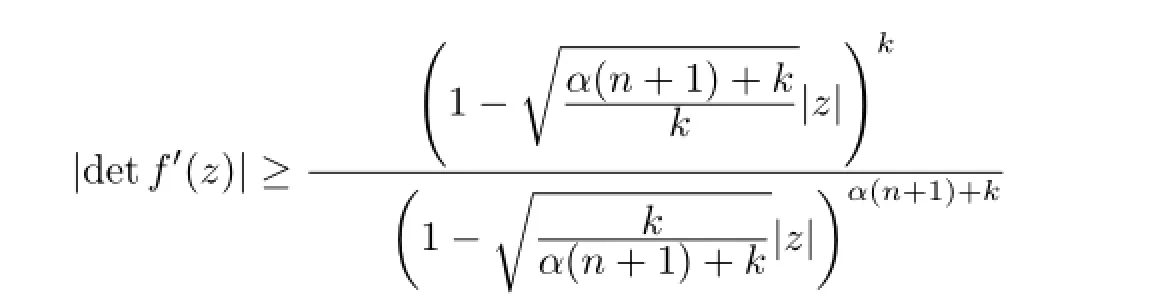
Proof(a)For a fixed ξ∈∂Bn,let

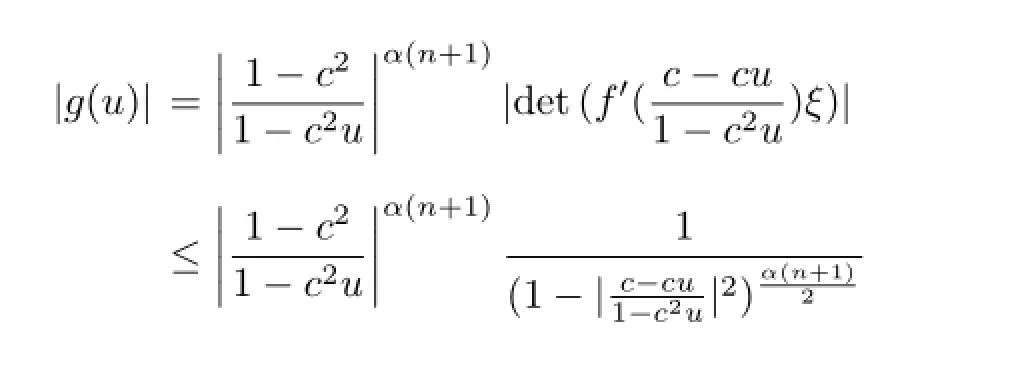
Then g(D)⊂D.Lemma 2.1(1)shows that|g(u)|≥ukfor u∈[0,1].Therefore,

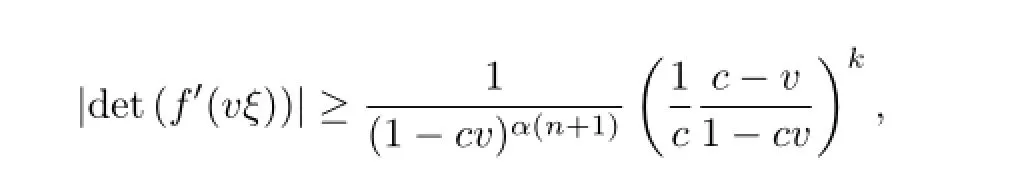
The proof of part(a)is complete.

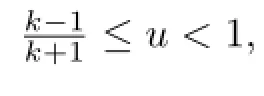
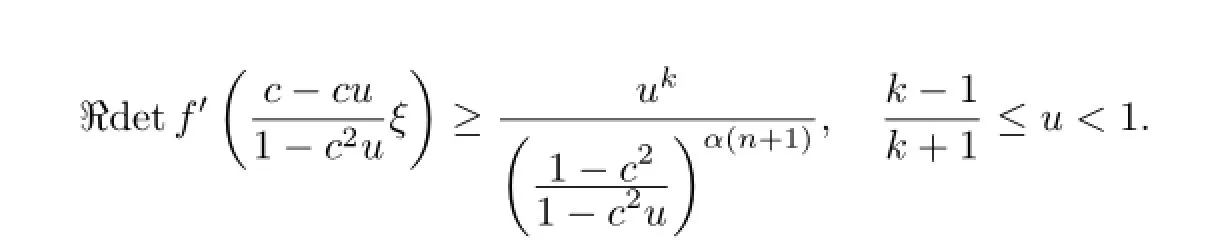
which gives the desired inequality.

Moreover,take F∈H(Bn)such that F(0)=0 and

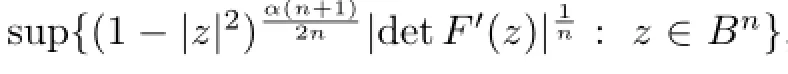
Therefore,

The last inequality follows by the elementary calculation

This shows that‖F‖0=1 and the proof of Theorem 3.1 is complete.

RemarkWhen n=1,α=1,Theorem 3.1 reduces to the main Theorem in[9].When n=1,k=1,α=1,Theorem 3.1 reduces to the Bonk’s Distortion Theorem in[3].

Setting k→+∞,we can easily obtain the following Corollary 3.2.

CorollaryIf f∈Hloc(Bn),‖f‖0,α=1 and det f′(0)=1,then

holds for all z∈Bn.Moreover,the above inequality can not be improved.

ProofNote that Hloc(Bn)⊂Hk(Bn),Theorem 3.1 shows

holds for all integer k.Some simple calculations give

Hence the proof of Corollary 3.2 is complete.

As an application of Theorem 3.1,the estimate of Bloch constant with respect to βαk(M)is given as follows.

Theorem 2The Bloch constant Bk,α(M)of Bαk(M)satisfies the following inequalities

Proof Let

Then M1−n≥Bk,α(M).Our goal is to show

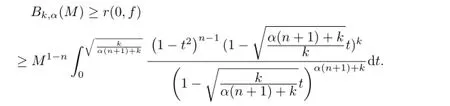
Notice that f∈Bαk(M)and det(f′(0))=1,there exists a small unit ball centered at the origin such that the mapping f biholomorphically maps the small ball onto another small ball in the range.If the ball in the range expands,the primage arrives at a point of of∂Bnor arrives at a point z0such that det(f′(z0))=0.Otherwise,we can enlarge the ball in range f(Bn) from the estimate of det(f′(z))in Theorem 3.1.It shows that we need to consider the case of det(f′(z))/=0.Let a straight line interval Γ⊂f(Bn).The interval Γ starts at f(0)and goes as far as it can with its preimage not running the boundary of Bnor det(f′(z))=0.Note that r(0,f)is the largest positive number r such that there exists a domain V⊂Bnand f biholomorphically maps V onto a ball centered at f(0)with radius r,thus

where γ=f−1(Γ).

By Lemma 2.2,it yields

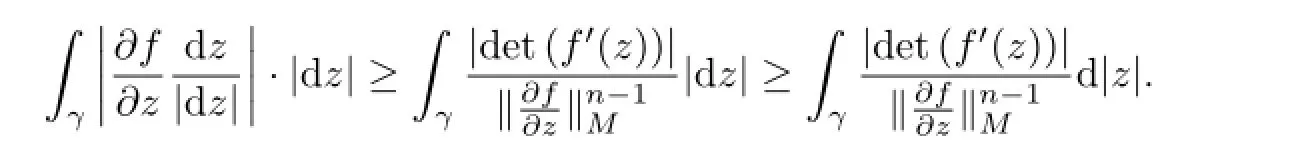
In terms of Theorem 3.1 and Lemma 2.2,we then estimate the right-hand side of the preceding inequality is greater than or equal to

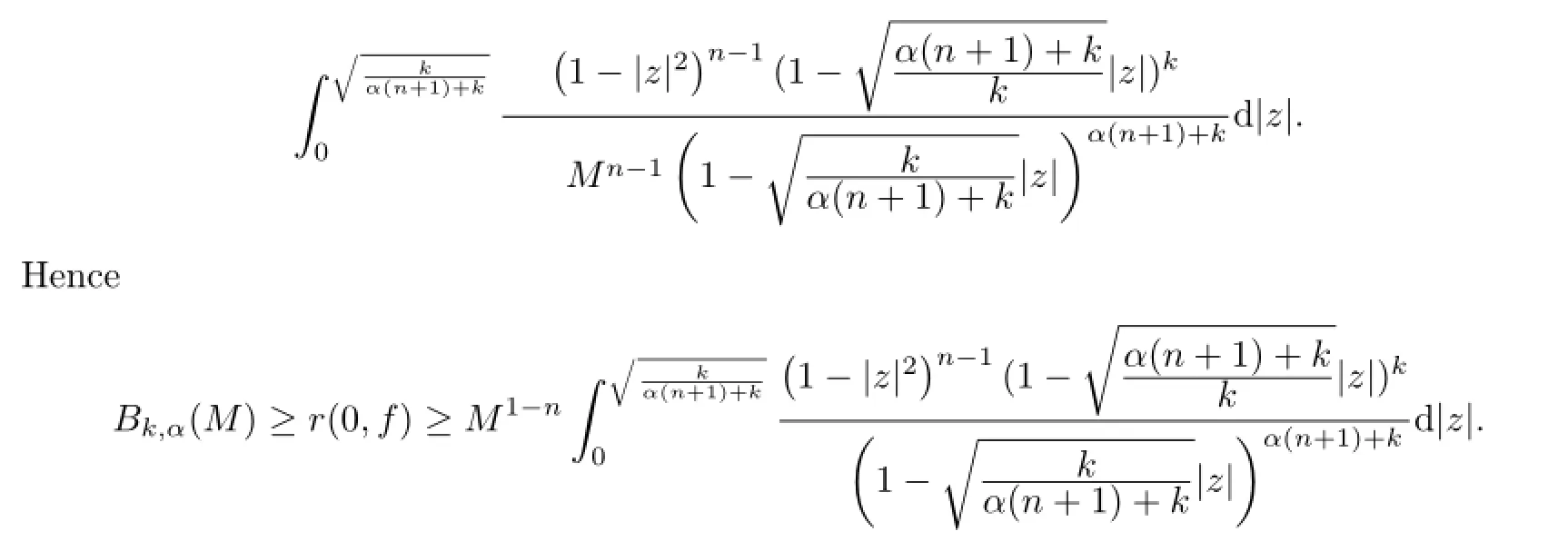
The proof of Theorem 3.3 is complete.

If k→∞,we then get the following estimate of Bloch constant Bloc,α(M)with respect to the local biholomorphic mappings of α-Bloch mappings.

Corollary The Bloch constant Bloc,α(M)estimate satisfies the following inequalities

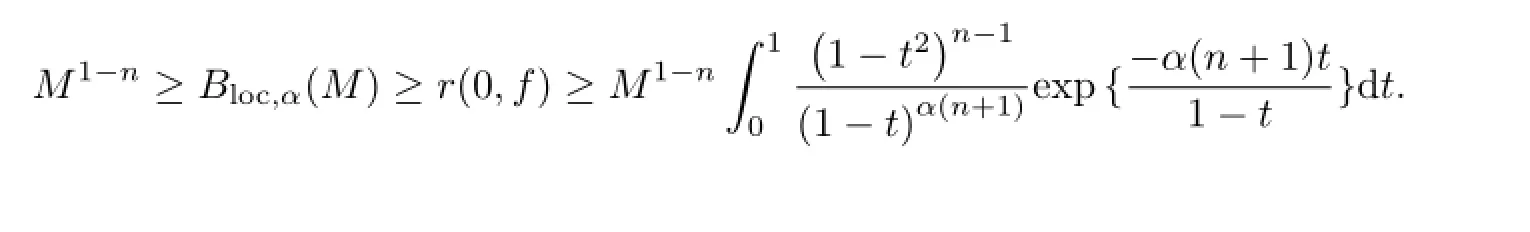
[2]BOCHNER S.Bloch theorem for real variables[J].Bull Amer Math Soc,1946,52:715-719.

[3]BONK M.On Bloch’s constant[J].Proc Amer Math Soc,1990,110:889-894.

[4]CHEN Shao-lin,PONNUSAMY S,WANG Xian-tao.Landau-Bloch constants for functions in α-Bloch spaces and Hardy spaces[J].Complex Anal Oper Theory,2012,6:1025-1036.

[5]FITZGERALD C,GONG Seng.The Bloch theorem in several complex variables[J].J Geom Anal,1994,4: 35-58.

[6]HAHN K.High dimensional generalizations of the Bloch constant and their lower bounds[J].Trans Amer Math Soc,1973,179:263-274.

[7]HARRIS L.On the size of balls covered by analytic transformations[J].Monatschefte f¨ur Mathematik,1977, 83:9-23.

[8]LIU Xiang-yang.Bloch functions of several complex variables[J].Pacific J Math,1992,52:347-363.

[9]LIU Xiang-yang,MINDA D.Distortion theorem for Bloch functions[J].Trans Amer Math Soc,1992,333: 325-338.

[10]TAKAHASHI S.Univalent mappings in several complex variables[J].Ann Math,1951,53:464-471.

[11]TERADA T,YANAGIHARA H.Sharp distortion estimates for p-Bloch functions[J].Hiroshima Math,2010, 40:17-36.

[12]WANG Jian-fei,LIU Tai-shun.Distortion theorem for Bloch mappings on the unit ball Bn[J].Acta Math Sin(Engl Ser),2009,25:1583-1590.

[13]WANG Jian-fei,LIU Tai-shun.Bloch constant on a classical domain of the first type[J].Acta Math Sinica(Chin Ser),2012,55:27-40.

[14]WU Hung-hsi.Normal families of holomorphic mappings[J].Acta Math,1967,119:193-233.

[15]YAN Zhi-min,GONG Sheng.Bloch constant of holomorphic mappings on bounded symmetric domains[J]. Science in China,1993,36A:285-299.

tion:32H02,30C55

:A

1002–0462(2017)01–0079–09

date:2016-10-23

Supported by the National Natural Science Foundation of China(11471111,11571105, 11671362);Supported by the Natural Science Foundation of Zhejiang Province(LY16A010004)

Biographies:LIU Zhi-bin(1965-),male,native of Jinhua,Zhejiang,an associate professor of Zhejiang Normal University,Ph.D.,engages in complex analysis;WANG Jian-fei(1978-),male,native of Jinhua,Zhejiang,an associate professor of Zhejiang Normal University,Ph.D.,engages in complex analyst.

CLC number:O174.56