带固定利息力风险模型下的累积分红现值

王 晶 晶

(宿州学院数学与统计学院， 安徽 宿州 234000)



带固定利息力风险模型下的累积分红现值

王 晶 晶

(宿州学院数学与统计学院， 安徽 宿州 234000)

研究带有固定利息力风险模型的破产问题，将理赔过程从齐次Poisson过程推广到对现实描述能力更强的更新过程，进而得到累积分红现值的矩母函数及其所满足的积分-微分方程。

利息力； 风险模型； 矩母函数； 积分-微分方程

风险理论是精算数学研究的核心内容，它是研究和处理保险实务经营中的随机风险模型，从定量的角度来研究保险公司经营的安全性。近年来，具有分红策略的风险模型受到越来越多的关注。自1957年De Finetti在风险模型中提出分红策略以来，很多学者开始研究分红策略下的风险模型，相比经典风险模型而言，可以更真实地刻画保险公司的营运状况。

破产理论是金融和保险领域中的风险理论的重要组成部分，破产理论的研究是在基于风险模型分析的基础上进行的。破产理论中的核心问题之一就是将盈余过程小于0的时刻定义为破产时刻，进而考虑其破产概率或Gerber-Shiu罚金函数等破产问题。 研究考虑门限分红策略下，资产盈余具有利息收入的破产风险模型，其累积分红现值的均值及矩母函数作为进一步研究Gerber-Shiu罚金函数的依据。

1 预备知识

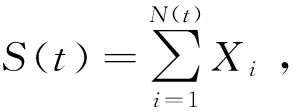
(1)

式中：u—— 保险公司的初始盈余；

c—— 单位时间的保费收入；

δ—— 保险公司将盈余投资于证券或银行所获得的固定利息力，δ>0。

在此基础上，我们考虑门限分红策略下资产盈余具有利息力收入的破产风险模型：

(2)

模型(2)表示：当盈余小于门限值a时，其保费收取率为c1；当盈余超过a时，保费收取率为c2(0

定义破产时刻T=inf{t≥0,Uδ(t)≤0}。

D(t)表示[0,t]内的所有累积分红，用α(α>0)表示分红折现因子，则到破产时刻T的所有累积分红现值为

由于不同的取值范围其表达式不同，有

(3)

假设式(3)在其定义域上连续可微。

2 M(u,y,a)满足的积分-微分方程

定理1 在模型(2)中，到破产时刻所有累积分红现值的矩母函数满足下面的方程：

(4)

(5)

证明 由于盈余过程{Uδ(t),t≥0}的Markov性，有

M(u,y,a)=E[M(Uδ(t),ye-αt,a)]+o(t)

(1-λt)M1(m1,ye-αt,a)+o(t)

(6)

由泰勒定理知

M1(m,ye-αt,a)=M1(u,y,a)+(δu+c2)t·

(7)

将式(7)代入式(6)，得

两边同时除以t，并令t→0，有m1→u，M1(m1-x,ye-αt,a)→M1(u-x,y,a)，M2(m1-x,ye-αt,a)→M2(u-x,y,a)，化简即为式(1)。

(8)

类似于式(4)的证明，可证得式(5)。

3 Vn(u,a)满足的积分-微分方程

定理2 在模型(2)中，到破产时刻所有累积分红现值Du,a的n阶原点矩满足下面的积分-微分方程：

u≥a

(9)

(λ+nα)Vn2(u,a) = 0

0

(10)

当n=1时，可得到累积分红均值V(u,b)=E[Du,a]。

4 结 语

为了得到与现实更为接近的风险模型，许多学者开始考虑其他分红策略下的风险模型，如线性红利界策略下的风险模型、非线性红利界策略下的风险模型、多重门限分红策略下的风险模型等。此次研究在门限分红策略下的风险模型问题，模型相对来说对保险公司实际的运营情况描述并不是十分全面，有待进一步完善。

[1] 严颖，成世学，程侃.运筹学随机模型[M].北京：中国人民大学出版社,1995:31-60.

[2] 吴荣，杜勇宏.常利率下的更新风险模型[J].工程数学学报,2002,19(1):46-54.

[4] YUEN K C，ZHOU M，GUO J. On a Risk Model with Debit Interest and Dividend Payments[J].Statist.Probab.Lett,2008,78(15):2426-2432.

[4] LIU D,LIU Z. The Perturbed Compound Poisson Risk Model with Linear Dividend Barrier[J].J.Comput Appl.Math,2011,235(8):2357-2363.

[5] 孙景云.门限分红策略下复合Poisson风险模型的绝对破产[J].山东大学学报，2010，45(3):105-110.

[6] 彭丹，侯振挺，刘再明.常利率和门限分红策略下带干扰的泊松风险模型的绝对破产问题[J].应用数学学报,2012,35(5):855-866.

[7] 王春伟，尹传存.绝对破产下具有贷款利息及常数分红界的扰动复合Poisson风险模型[J].数学物理学报,2010,30(1):31-41.

[8] 陈昱，苏淳.有利息力情形下的有限时间破产概率[J].中国科技大学学报,2006(5):909-916.

The Discounted Dividend Payments in the Risk Model With Constant Force of Interest

WANGJingjing

(School of Mathematics and Statistics,Suzhou University, Suzhou Anhui 234000, China)

In this paper, we consider the ruin problems in the risk model with constant force of interest. We will extend the claim process from the homogeneous Poisson process to a more realistic description of the renewal process. Furthermore, we derive the moment generating function and integro-differential equations of the discounted dividend payments.

interest force; risk model; moment generating function; integro-differential equations

2016-11-02

国家自然科学基金项目(11371029)；安徽省高校自然科学研究项目(KJ2016A770)；安徽省优秀青年人才支持计划重点项目(gxyqZD2016340)

王晶晶(1987 — )，女，宿州学院助教，研究方向为保险精算。

O211.6

A

1673-1980(2017)03-0123-02