基于曲线拟合的电池剩余放电时间预测研究
2017-06-05丁学利李玉叶
丁学利 李玉叶
(1. 阜阳职业技术学院基础教学部, 安徽 阜阳 236031;2. 赤峰学院数学与统计学院, 内蒙古 赤峰 024000)
基于曲线拟合的电池剩余放电时间预测研究
丁学利1李玉叶2
(1. 阜阳职业技术学院基础教学部, 安徽 阜阳 236031;2. 赤峰学院数学与统计学院, 内蒙古 赤峰 024000)
为解决铅酸电池的放电时间预测问题,利用最小二乘拟合将电池放电曲线分成2个非线性段进行曲线拟合,建立了整体的放电曲线模型。预测了电池剩余放电时间,最后用平均相对误差MRE评估了模型的精度。该模型可为研究电池放电特性提供借鉴,也为铅酸电池的生产和使用提供参考。
曲线拟合; 放电曲线; 剩余放电时间; 平均相对误差
铅酸电池作为电源在军事、工业和日常生活中被广泛应用。电池在当前负荷下还能供电多长时间(即以当前电流强度放电到额定的最低保护电压Umin时的剩余放电时间)是使用中必须了解的。铅酸电池从充满电开始放电,电池电压随时间变化的关系称为放电曲线。关于电池放电曲线的研究,文献[1-6]提出了多种电池放电模型。文献[4]建立了三阶等效电路模型,文献[5]利用递归神经网络模型来估计电池放电曲线,文献[6]将电池放电曲线分成线性段和非线性段,从而建立了统一的电池放电曲线模型。
此次研究是在文献[6]中电池放电曲线模型的基础上,以2016年“高教社杯”全国大学生数学建模竞赛C题[7]为例,将电池放电曲线分成2个非线性段进行曲线拟合,建立了整体的放电曲线模型。利用该模型可以较准确地预测电池剩余放电时间。为研究电池放电特性和电池放电实验提供参考。
1 数据分析
根据2016年全国大学生数学建模竞赛C题附件1[7]中的数据可作出各电流强度下电池的放电曲线,如图1(a)所示。电池开始放电时电池电压快速下降,处于不稳定状态,放电一段时间后,电池处于稳定放电状态,最后电池电即将放完时,电压随时间快速下降。由于电池在开始放电时不稳定,称为暂态阶段,因此可以将图1(a)中的不稳定放电数据删除,不会影响电池放电的整体趋势。研究将数学建模竞赛C题附件1中电流强度为20 A的前200 min的数据,以及电流强度在30~100 A的前50 min的数据删除。删除数据之后的放电曲线如图1(b)所示。拟合精度采用平均相对误差MRE,即在附件1表中从额定的最低保护电压(Umin,文中为9 V)开始按不超过0.005 V的最大间隔提取231个电压样本点。这些电压值对应的模型已放电时间与采样已放电时间的平均相对误差即为MRE[7]。
2 模型的建立
根据图1(b)的放电趋势,以电流强度为20 A的放电曲线为例,若将放电曲线的开始段用直线拟合,则误差太大,如图2中虚线所示。因此考虑放电开始段采用二次多项式拟合,如图2中粗实线所示,拟合效果较好。由于放电结束段曲线呈指数快速衰减,因此考虑放电结束段用指数型函数进行曲线拟合。拟合效果可以用原始数值与拟合数值之间的相对误差的绝对值来描述,即相对误差的绝对值=∣原始数值-拟合数值∣/原始数值。放电开始段取的太短或太长都会使相对误差的绝对值变大。因此,放电开始段必然存在最佳的拟合时刻点,使相对误差的绝对值达到最小。图3是电流强度为20 A时,放电开始段的放电时间百分比与相对误差的绝对值的关系图。可以看出大约在放电总时间的55%处相对误差的绝对值达到最小(图中箭头所示)。因此,放电开始段的终止时间大约选取在放电总时间的55%处。电流强度为30~100 A时,有类似结论,在此就不一一阐述。
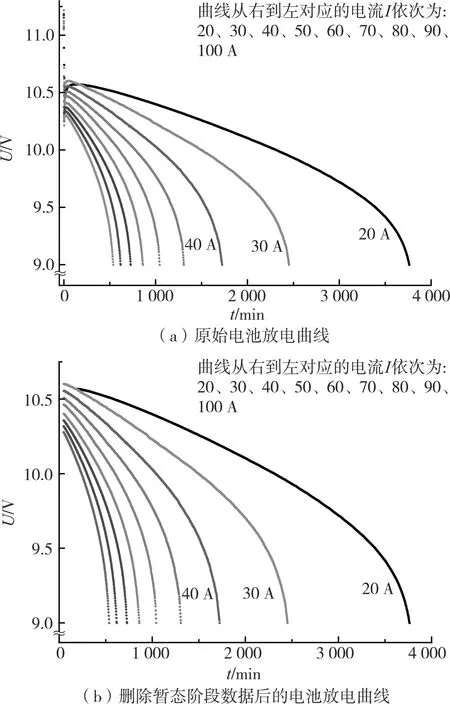
图1 不同电流强度下电池放电曲线

图2 电池(电流强度为20 A)放电开始段的拟合效果

图3 电流强度为20 A时放电时间百分比与相对误差的绝对值的关系
根据上述分析,可将放电曲线分成放电开始段和放电结束段进行曲线拟合。放电开始段采用二次多项式进行曲线拟合,放电结束段采用指数型函数进行曲线拟合。建立模型如下:
V(t)=a0+a1t+a2t2-exp[b(t-t0)+c]
(1)
式中:a0,a1,a2—— 二次多项式的拟合系数,均为常数;
b,c—— 指数型函数的拟合系数,均为常数;
t0—— 放电开始段的终止时间,t0取放电总时间的55%。
为了建立电池以20A到100A之间任一恒定电流强度放电时的放电曲线的数学模型,将模型(1)中的拟合系数a0,a1,a2,b,c和t0分别看成关于电流强度I的函数,再对其进行曲线拟合。建立模型如下:
V(t,I)=a0(I)+a1(I)t+a2(I)t2- exp[b(I)(t-t0(I))+c(I)]
(2)
其中,
a0(I)=a00+a01Ia1(I)=a10+a11I
a2(I)=a20+a21I+a22I2
b(I)=b00+b01Ic(I)=c00+c01I
3 模型的求解
利用模型(1)可以拟合不同电流强度下的放电曲线。表1中t0取放电总时间的55%,其余参数则是根据模型(1)采用最小二乘拟合得到的在不同电流强度下的拟合系数,其拟合曲线如图4所示。计算不同电流强度下的MRE值,如表2所示,其值均未超过1‰,拟合效果较好。根据模型(1),当电池分别在30、40、50、60、70A电流强度下放电,测得电压都为9.8V时,电池的剩余放电时间分别约为610、441、339、281、257min。

表1 不同电流强度下的拟合系数

图4 不同电流强度下的放电电压随时间变化的拟合曲线
根据表1中数据的特点,t0(I)用指数型函数拟合,a2(I)用二次多项式拟合,a0(I),a1(I),b(I)和c(I)都用直线拟合,其拟合系数见表3。图5是t0(I),a0(I),a1(I),a2(I),b(I)和c(I)的拟合结果。除系数c拟合效果较差之外,其余的拟合效果较好。但系数c(I)对拟合曲线不起决定作用,因此对模型(2)的影响较小。
由表3的拟合系数可得t0(I),a0(I),a1(I),a2(I),b(I)和c(I)的函数表达式,从而利用模型(2)可计算电池从20A到100A之间以任一恒定电流强度放电时的放电曲线。表4是电流强度为 55A时模型(2)的各个系数值,其放电曲线如图6所示。图6中粗实线是电流强度为55A的预测曲线,细实线和点线分别是电流强度为50A和60A的实测曲线。电流强度为55A的放电曲线在10V、9.8V、9.5V、9V对应的已放电时间约为682、868、1 056、1 178min;相应的剩余放电时间分别为496、310、122、0min。

表2 不同电流强度下的平均相对误差MRE

表3 各拟合系数

图5 各系数拟合结果

表4 电流强度为55 A时模型(2)的各系数值

图6 电池电压随放电时间的变化曲线
4 结 语
通过最小二乘拟合建立铅酸电池放电时间预测的数学模型,得到了电池从20 A到100 A之间以任一恒定电流强度放电时的放电曲线。该模型可较准确地预测电池剩余放电时间。但由于t0(I),a0(I),a1(I),a2(I),b(I)和c(I)是通过最小二乘拟合得到的,所以在拟合的过程中会产生一定的误差,从而会影响模型(2)的预测精度,因此模型(2)的拟合效果还有进一步提升的空间。
[1]CHENM,RINCON-MORAGA.AccurateElectricalBatteryModelCapableofPredictingRuntimeandIVPerformance[J].EnergyConversion,IEEETransactionson, 2006,21(2):504-511.
[2]TIANS,HONGM,OUYANGM.AnExperimentalStudyandNonlinearModelingofDischargeI-VBehaviorofValve-regulatedLead-acidBatteries[J].EnergyConversion,IEEETransactionson,2009,24(2):452-458.
[3]PAPICI.SimulationModelforDischargingaLead-acidBatteryEnergyStorageSystemforLoadLeveling[J].EnergyConversion,IEEETransactionson,2006,21(2):608-615.
[4]CERAOLOM.NewDynamicalModelsofLead-acidBatteries[J].PowerSystems,IEEETransactionson,2000,15(4):1184-1190.
[5]CAPIZZIG,BONANNOF,TINAGM.RecurrentNeuralNetwork-basedModelingandSimulationofLead-acidBatteriesCharge-discharge[J].EnergyConversion,IEEETransactionson,2011,26(2):435-443.
[6] 王占江. 阀控式铅酸蓄电池实验平台的设计与建模方法的研究[D]. 秦皇岛:燕山大学,2014:10-20.
[7] 2016年全国大学生数学建模竞赛.http://www.shumo.com/home/(2016-10-25).
Research on the Prediction of Residual Discharge Time of Battery Based on Curve Fitting
DINGXueli1LIYuye2
(1.Department of Basic Education, Fuyang Institute of Technology, Fuyang Anhui 236031, China; 2.Mathematics and Statistics Institute of Chifeng University, Chifeng Inner Mongolia 024000, China)
In order to predict the discharge time of the lead acid battery, the discharge curve is divided into two nonlinear sections and fitted by the least squares fitting; thus, the whole discharge curve model is established. The discharge time of the battery is predicted on the basis of discharge curve model. Finally, the accuracy of the model is evaluated by the average relative error MRE. The model not only provides a theoretical basis for the study of battery discharge characteristics, but also offers an important basis for the production and use of lead-acid batteries.
curve fitting; discharge curve; residual discharge time; mean relative error
2016-11-15
国家自然科学基金青年科学基金项目“具有共存行为的神经元所组成网络的时空动力学行为研究”(11402039);内蒙古自然科学基金面上项目“基于化学自突触组成的视皮层神经元网络的时空动力学行为研究”(2016MS0101);安徽省自然科学一般项目“神经系统产生螺旋波的动力学机制研究”(KJ2015B008)
丁学利(1982 — ),男,硕士,阜阳职业技术学院副教授,研究方向为非线性动力学与数学建模。
O241.2
A
1673-1980(2017)03-0125-05
