一个紧凑的素数分布规律
2017-06-05王宇
王 宇
(成都理工大学 信息科学与技术学院,成都 610059)
一个紧凑的素数分布规律
王 宇
(成都理工大学 信息科学与技术学院,成都 610059)
素数规律不能精确地描述,但可以用阈值的方式对素数规律进行描述。本文介绍了一个迄今最紧凑的素数分布定律:在连续奇素数序列中,假定p、q是2个临近的奇素数,p 素数;分布;连续奇合数;紧凑 如果说数论是数学的皇冠,则素数理论为皇冠上的珠宝。诸如哥德巴赫猜想、孪生素数分布这样的数论猜想极大地丰富了数论领域。数论领域的一个重要研究方向为素数的分布[1-3]。 素数分布的研究思路主要有2类,一类是平均分布,代表是素数定理,以渐进公式表示;另外一类是素数间隔上限,等价于最大连续奇合数个数,代表为伯特兰-契比雪夫定理,还有3个猜想,为Legendre猜想[4]、Oppermann猜想[5]、Andrica猜想[6]。 伯特兰-切比雪夫定理是指1845年约瑟·伯特兰提出的猜想。1850年切比雪夫证明了这个猜想。拉马努金给出较简单的证明,而保罗·艾狄胥则借二项式系数给出了另一个简单的证明。 伯特兰-切比雪夫定理的描述是:给定整数n> 3,则至少存在一个质数p,符合n Legendre猜想[4]就是,对于自然数n,在区间[n2, (n+1)2]必定存在一个素数。 它是Landau数论难题中的第三个。 Oppermann猜想[5]则是,对于n>1的整数,在下列2个区间各存在至少1个素数:[n(n-1),n2]和[n2,n(n+1)]。 本文属于第二类情况,即考虑素数分布上限值,所给出的范围,将比上面提到的定理和猜想把素数的密度限制在更窄的范围内。 本文提到的素数定理和伯特兰-切比雪夫定理是经过证明为正确的,为定理;而Legendre猜想,Oppermann猜想,Andrica猜想以及本文提出的定律,还有哥德巴赫猜想,是从客观大量实例总结出来的结论,目前难以证明;它们中的某个定律一旦被证明,则一系列相关问题将得到解决,在该领域带来重大影响。 本文中符号的含义如下:g ——奇数; p, q ——相邻的2个奇素数, p 除2外,所有的素数都是奇数。我们关注的问题是:间隔多少个奇数后必定有一个奇素数呢?这个问题,换个角度就是,间隔多少个奇合数后,必定存在一个奇素数?为方便描述该问题,我们先给出几个定义。 定义1 奇数序列指1, 3, 5, 7, 9, 11, …。但是1既不是素数,也不是合数,所以本文只研究大于等于3的奇数序列。定义不小于3的奇数序列X为不小于3的奇数组成:3, 5, 7, 9, 11, …; 该序列上奇数g对应的位置号w(g),其值分别为1, 2, 3, 4, 5, …; 即w(3)=1, w(5)=2, w(7)=3, w(9)=4, …, w(g)=(g-1)/2。w(g)数值的含义为不小于3且不大于g的奇数个数。 可得 (A) 所有的奇素数都大于等于3,所有的奇合数都大于等于3。所以重点关注不小于3的奇数,为区别,记不小于3的奇数序列为大写字母X。 定义2 素数序列为2, 3, 5, 7, 11, 13, 17, …。其中只有2是偶数,其余所有的素数都是奇数。奇素数序列为素数序列中大于2从小到大排列的素数,即3, 5, 7, 11, 13, 17, …。该序列上奇素数p对应的位置号V(p)的值分别为1, 2, 3, 4, 5, …; 即V(3)=1,V(5)=2,V(7)=3,V(11)=4, …。V(p)数值的含义为不大于p的奇素数个数。 若p和q是奇素数序列中2个相邻奇素数,且q>p,则有V(q)=V(p)+1。例如V(11)=V(7)+1。 定义3 假设p为一个奇素数,则称所有的p×a(表示p乘以a,a为大于1的奇数)为p所产生的奇合数。 根据定义,p所产生的奇合数有3p, 5p, 7p, 11p, …即为奇数序列X中各个奇数与p的乘积,包含了p的大于1的奇数倍数。 根据上面的性质,马上又可以得到: 性质2 奇素数序列3, 5, 7, 11, …, p, q;即p和q是奇素数序列中2个相邻奇素数, p≤q-2。不小于3的奇数序列X在区间[p2,q2)之间的任何一个奇合数g都能被一个不大于p的奇素数整除,即[p2,q2)内任何一个奇合数g除以不大于p的各个奇素数,至少一个余数是0。 根据性质2,我们可以把奇数序列X中不小于9的奇数划分成若干段来考虑,即 [32,52)∪[52,72)∪[72,112)∪[112,132)∪…∪[p2,q2)∪… 下面我们给出一个素数分布的更小范围,称之为WY定律。 WY定律 奇素数序列3, 5, 7, 11, …, p, q, … ( p和q是2个相邻奇素数, p≤q-2)。除了2个变异奇数区间[115, 125]和[1 329, 1 359](连续奇合数个数分别为6和16),不小于3的奇数序列X在区间[3,q2)中的连续奇合数的个数不大于V(p);即在区间[3,q2),每V(p)+1个奇数中至少存在一个素数。 已验证1亿以内的情况,定律在1亿以内是成立的。 定律中的2个特殊区间,一个是[115, 125],另外一个是 [1 329, 1 359],2个奇数区间的连续奇合数个数分别为6和16,所对应的V(p)分别是V(7)=3, V(31)=10。 由WY定律,可以得到一个WY定律的性质。 WY定律的性质 奇素数序列3, 5, 7, 11, …, p, q, … ( p和q是其中2个相邻奇素数,且p≤q-2),则有 (B) 其次,一般情况下,在奇素数序列中,令p和q是其中的相邻奇素数,p 2w(p) 因存在合数,知道奇素数p在奇素数序列中的位置数值V(p)总是小于等于p在奇数序列中的位置数值w(p),即 V(p)≤w(p) 假设奇素数序列中2个相邻的奇素数为p′,q′,且p′ q>q′2/2 再次由伯特兰-切比雪夫定理,在区间[q′2/2,q′2/4]必定存在一个奇素数,则 p>q′2/4 该式子是p的下限值,p完全可以大于q′2/2,即p不必位于区间[q′2/2,q′2/4]。从这步也可以看出,WY定律对素数间隔的限定比该性质严格得多,尤其是当q′更大时的情况。 根据WY定律,在奇数区间[3,q′2)内,连续奇合数个数不大于V(p′),即2个相邻奇素数之差小于等于2×V(p′),则有 q-p≤2V(p′) ≤2w(p′) 即得 本节讨论基于如下题设:素数序列3, 5, 7, 11, …,p,q, … (p和q是其中2个相邻奇素数,p≤q-2)。 伯特兰-切比雪夫定理已经被用不同的方法证明。给定奇数g∈[p2,q2),知g≥p2。由伯特兰-切比雪夫定理,在g和2g之间存在一个素数,此时的间隔大小限制在g≥p2。而根据WY定律,间隔大小限制在2V(p) (p2-p)/p2=(p-1)/p。 随着素数的增大,WY定律越优秀。所以,我们的定律描述了更强的素数密度,性能远比伯特兰-切比雪夫定理优秀。 根据我们的定律,在区间[p2,q2)中的连续奇合数的个数≤V(p),则对于正整数n(p≤n 根据我们的定律,对于正整数n(p≤n 根据WY定律的性质(B)及该性质的推导过程,我们的定律比Andrica猜想更强[6]。 [1] 张贵文,张崇军,王瑞贞.素数的规律性和判定法[J].工程数学学报,1986,3(2):107-114. Zhang G W, Zhang C J, Wang R Z. The representation and distinguish method of prime numbers[J]. Journal of Engineering Mathematics, 1986, 3(2): 107-114. (in Chinese) [2] 赵改换,郑海务,高海燕,等.一种寻找质数分布规律的新方法[J].河南科学,2012,30(1):31-36. Zhao G H, Zheng H W, Qing H Y,etal. A new method of finding the distribution of prime numbers[J]. Henan Science, 2012, 30(1): 31-36. (in Chinese) [3] 赵改换,尤佳佳,孙健,等.质数分布规律的再探讨[J].河南科学,2015,33(4):506-508. Zhao G H, You J J, Sun J,etal. Further discussion of prime number distribution rule[J]. Henan Science, 2015, 33(4):506-508. (in Chinese) [4] Weisstein E W. Legendre’s Conjecture[M/OL]. [2016-09-02]. http://mathworld.wolfram.com/LegendresConjecture.html [5] Maier H. Primes in short intervals[J]. Michigan Mathematical Journal, 1985, 32(2):193-205. [6] Andrica D. Note on a conjecture in prime number theory[J]. Studia Univ Babes-Bolyai Math, 1986, 31(4): 44-48. A compact distribution law of prime numbers WANG Yu CollegeofInformationScience&Technology,ChengduUniversityofTechnology,Chengdu610059,China Although the distribution of prime numbers can not be described accurately, the law of prime number distribution can be described by threshold values. In the article, the most compact prime distribution law is presented to cope with the problem. Letp,qbe two serial ones among the odd prime number serial,p prime number; distribution; consecutive odd composite numbers; compact 10.3969/j.issn.1671-9727.2017.03.11 1671-9727(2017)03-0373-04 2016-10-09。 [作者简介] 王宇(1973-),男,博士,副教授,研究方向:Qos选路算法、软件工程、初等数论, E-mail:wangyu@cdut.edu.cn。 O156.1 A1 概 述
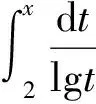

2 最大连续奇合数个数

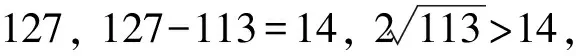
3 总 结
