一种基于离散观测器的DC/DC变换器参数在线辨识方法

2017-06-05吴杭举周雒维

电源学报 2017年3期

关键词：观测器电感电容

吴杭举，周雒维

（重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400044）

一种基于离散观测器的DC/DC变换器参数在线辨识方法

吴杭举，周雒维

（重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400044）

针对功率变换器参数在线辨识问题，提出了一种新的基于离散观测器的DC/DC变换器主电路参数非侵入式在线辨识方法。基于Lyapunov函数提出了一种用于离散系统参数辨识的观测器算法，进一步引入模型噪声估计使得观测器能够适用于经低速采样离散化的混杂系统的参数辨识。为将提出的观测器应用到DC/ DC变换器参数辨识中，以Buck变换器为例给出了DC/DC变换器离散模型的建立方法。在此基础上，设计了用于Buck变换器主电路参数辨识的离散观测器。观测器根据电感电流、输出电压以及控制器输出即可对滤波电感及其等效串联电阻、滤波电容及其等效串联电阻、负载等效电阻等多个参数进行在线辨识。仿真和实验结果验证了该方法的有效性。

Buck变换器；参数在线辨识；低采样率；在线监测；参数观测器

近几十年来，功率变换器在新能源发电、电动汽车、电子照明和直流输电等领域中应用越来越广泛，电力电子系统的可靠性评估以及健康管理得到了工业界的广泛关注。运行过程中，主电路电容、电感等器件会逐步老化，系统可靠性不断降低［1,2］。器件的老化往往伴随着其电路参数的变化，变换器在线参数辨识技术能够为系统可靠性评估以及健康管理提供数据支持，很有研究意义。

变换器在线参数辨识可以分为单元件参数辨识［3-16］和多元件参数辨识［17-25］两种。由于电容是变换器中最容易失效的器件之一［1］，单元件参数辨识的研究主要集中在对电容参数的辨识。相对于单一元件（电容）参数的在线辨识，多元件参数在线辨识方法的研究更具现实意义和挑战性。多元件参数的辨识结果不仅能为状态评估和健康管理提供数据，还能指导控制器特别是基于模型的控制器［17-19］的设计和调整。文献［20,21］通过建立变换器混杂系统模型，使用最小二乘法辨识多种参数；文献［22］建立Buck电路滤波网络输入输出传递函数模型，采用遗传算法辨识主电路参数；文献［23］提出了一种用于参数估计的滑模观测器，并介绍了其在Buck变换器电容容值和负载电阻值估计中的应用方法。上述文献中的方法均需要较高的采样频率。文献［24］提出一种状态观测器算法用于DC/DC变换器参数估计，采样率要求低，但需要测量阶跃响应；文献［25］提出的基于多目标优化算法的变换器在线监测方法，实现了低采样速率的参数辨识，且具有优秀的抗噪声干扰能力，但需要引入伪随机二进制扰动。

针对现有多参数辨识方法难以同时满足低采样率和不影响变换器正常运行的现状，本文提出了一种新的适用于变换器参数辨识的离散观测器算法，并以Buck变换器为例进行了详细介绍。观测器算法根据变换器输出电压和电感电流的采样值以及控制器输出即可实时在线辨识出变换器滤波电感、滤波电感等效串联电阻 ESR（equivalent series resistance）、滤波电容、滤波电容ESR和负载等效电阻等多种参数，且对采样率的要求相对较低，对变换器运行无影响。首先给出了所提观测器的原理和设计方法，然后以Buck变换器为例介绍了用于观测器设计的开关变换器离散模型的建立方法。设计了用于Buck变换器参数辨识的观测器，进行了仿真和实验验证。

1 观测器原理

由于变换器中开关切换的存在，系统既表现出连续动力行为，又表现出离散动力行为，因此变换器是一种典型的混杂系统。在实际应用中常要求辨识方案成本较低，因此辨识系统的采样频率和计算资源常受到限制，离散模型能方便地描述低采样率的系统，因此相对连续模型或混杂模型的离散模型更适合在线监测系统的设计。本节将文献［23］中的连续域滑模观测器扩展到离散域，并进一步引入模型噪声估计，提出了一种低采样率要求的适用于变换器电路参数辨识的观测器算法。离散系统模型为

式中：x（k）为n个可测量的状态或者输入构成的向量，x（k）=［x1（k）x2（k）…xn（k）］T，它们线性无关；cT为n个系统待估计参数构成的向量，cT=［c1c2…cn］；ξ为模型噪声，表示模型中其余的非线性项；y为系统输出。建立观测器预测方程为

g（k）对应于文献［23］中的等效控制量。由于对于变换器在线参数辨识，采样频率不宜过高，不可能用滑模观测器中所使用的符号函数控制等方法使观测器进入滑动模态，不过在线辨识应用对观测器的实时性要求并不高，本文直接使用预测误差量代替滑模观测器中的符号函数。

设观测器更新方程为

则有

由上述推导过程可知，这样设计的观测器是稳定的，稳态误差由模型噪声ξ决定。合理地选择增益ρ能扩大观测器吸引域，提高稳定性。

由于在线辨识系统采样频率较低，通常并不能简单地使用形如y（k+1）=y（k）+c（k）Tx（k）的仿射非线性模型近似描述变换器。直接将其用于预测方程的建立，会导致式（1）中ξ（k）较大，给参数估计带来较大的误差。因此需要在预测方程中引入模型噪声估计项，则式（2）的预测方程修改为

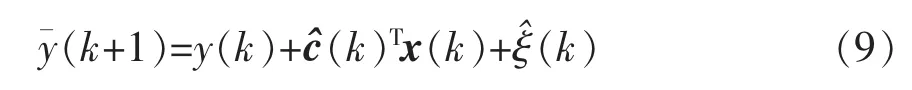
2 Buck变换器的离散模型

为将所提出的观测器算法应用到变换器参数在线辨识中，需要建立变换器的离散模型。以Buck变换器为例介绍变换器离散模型的建立方法。

Buck变换器是功率变换器中的基本变换器之一，其电路模型如图1所示。图中E为输入电压，S1、S2为半导体开关器件，L为滤波电感，rL为电感等效串联电阻，C为滤波电容，r为电容等效串联电阻，R为等效负载电阻。在变换器正常工作时，开关管S1、S2互补导通。当开关S1导通，S2截止时，开关函数u=1；S1截止，S2导通时u=0，控制开关管导通关断时间可实现直流降压功能。

对图1中的电路进行分析，可得到连续导通模式CCM（continuous conduction mode）下Buck变换器连续时域模型，即

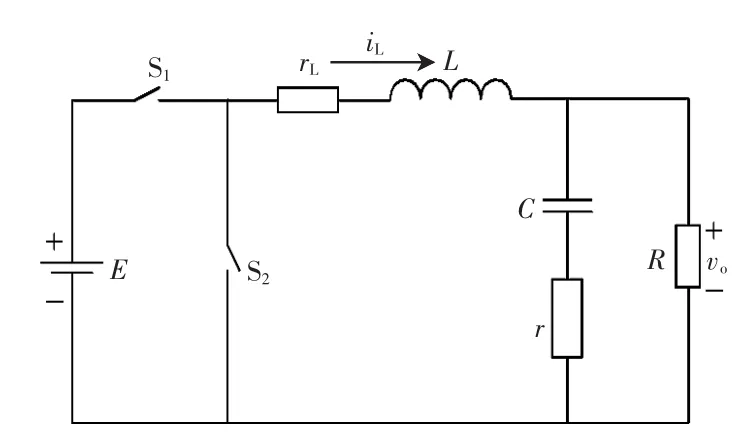
图1 Buck变换器电路原理Fig.1 Buck converter equivalent circuit

为对变换器参数进行在线辨识，需要对电感电流以及输出电压同步采样，假设采样率恒定，采样时间间隔为Ts，采样时刻将开关周期划分为多个子区间，如图2所示。图中采样时刻将一个开关周期划分为了5个区间，每个区间长度为Ts。

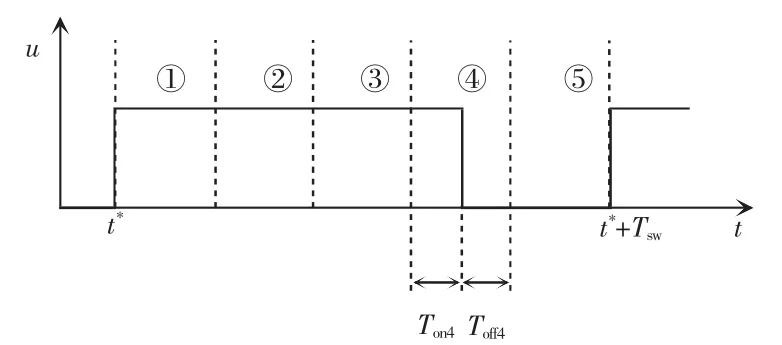
图2 开关周期子区间划分Fig.2 Subinterval division of switching period

为使结论具有通用性，以图中的子区间④为例分析Buck变换器离散模型。设子区间④起始时刻为k时刻，结束时刻为k+1时刻。根据Buck变换器连续域状态方程式（10），可得离散迭代映射P为

式中，ds为子区间④中的占空比，ds=Ton4/Ts。显然其他区间是区间④的特殊情况，因此式（12）适用于开关周期内的任何子区间。对于各种数字控制功率变换器，开关切换通常由数字控制器决定，因此ds容易确定。以后沿调制、每个开关周期更新一次占空比的Buck变换器为例，记为子区间序号为j，采样率为开关频率整数倍，从开关周期起始时刻开始采样，并将每个开关的第1个子区间序号置为1，如图2所示，则子区间j的占空比可表示为

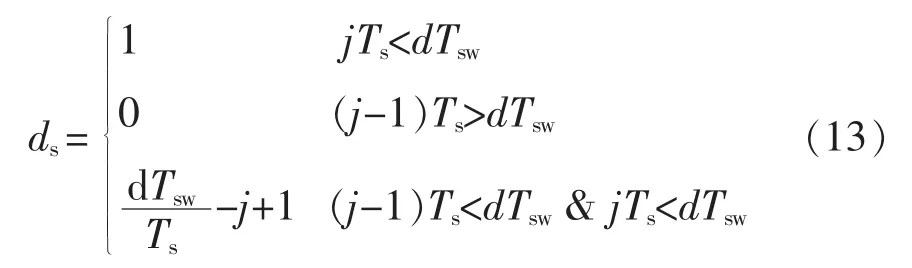
式中：j为子区间序号；Tsw为开关周期；d为一个开关周期的占空比，。

对于矩阵指数，计算公式为

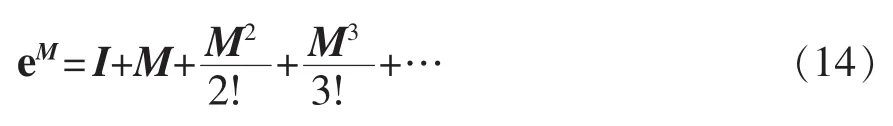
取矩阵指数的一阶近似，即eM≈I+M，代入式（12），可得到一阶近似的变换器离散模型为

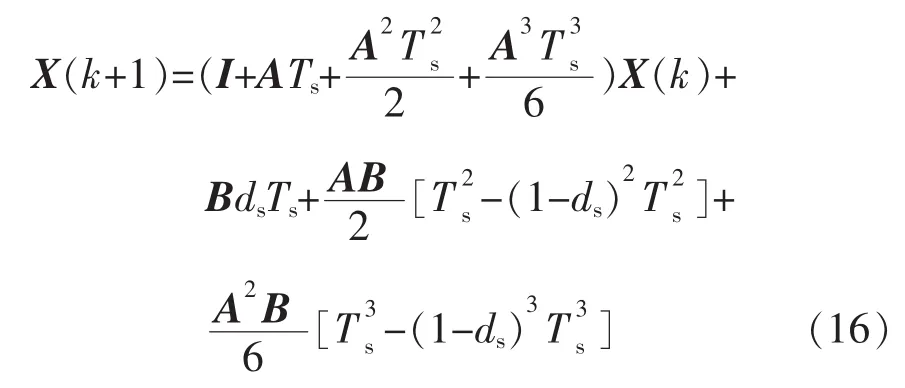
用于参数在线辨识的观测器设计将在上述2个离散模型的基础上进行。

3 Buck变换器的参数观测器设计

根据Buck变换器一阶近似的离散模型，可按照第1节的理论建立2个观测器，分别对变换器离散模型中的参数a和b进行估计。但在进行低速采样时，采用一阶模型，较大的模型噪声ξ会使参数估计出现较大误差。因此根据3阶模型在观测器预测方程加入模型噪声估计。根据式（5）、式（6）、式（8）、式（9）、式（15）、式（16）建立观测器如下。

预测方程为

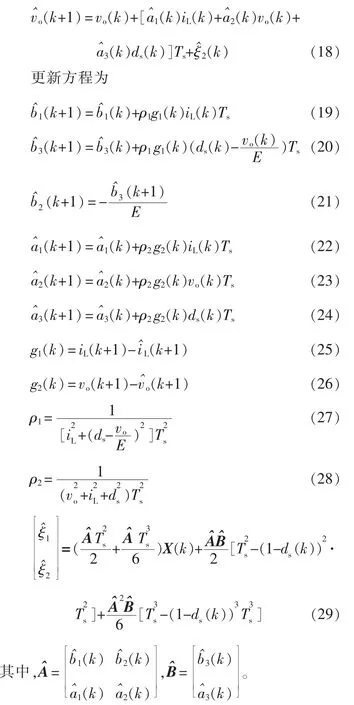
上述观测器中，预测模型即式（17）和式（18）是在一阶模型式（15）的基础上加入了模型噪声估计，估计项的计算函数式（29）为3阶模型中的2，3阶项。在更新方程式（19）～式（24）中输出误差仅用于直接修正一阶近似模型中的参数。可见加入该项进行模型噪声估计后，将代替ξ影响观测器稳态误差和收敛速率。在迭代过程中会随着参数估计误差下降而下降，从而降低观测稳态误差，并使得观测器的设计与模型为仿射非线性形式时一致，多输出系统与单输出系统一致，简化了设计。由于观测器的建立是基于Lyapunov函数，相对于扩展卡尔曼滤波器等常用的观测器具有更强的稳定性，这与,X（k））的性质有密切的关系。此外，需要指出Buck电路工作中，电感电流近似线性变化，其对输出电压纹波和电流纹波并不敏感，因此在电路处于稳态工作时有（其中，IL和Vo分别为电感电流和输出电压的直流分量），这使得同时对进行观测很困难，难以得到准确的结果。因此在观测器设计中，至少需要已知E、L、rL中一个量。假设E已知，则电感电流动力方程改写为，并按照第1节中的方法进行观测器设计，更新方程式（21）中b2（k）根据b3（k）计算得到的。

由式（10）中参数a和b与电路参数的对应关系可知，将观测器估计所得参数代入下列计算式中即可得到Buck变换器的元件参数的辨识值：。

4 仿真研究

为验证提出的在线辨识方法，本文在Matlab中对CCM Buck变换器和提出的观测器进行了仿真研究。仿真电路参数如表1所示。Buck变换器输入电压25 V，通过PI控制器进行电压闭环控制。将输出电压控制在12 V，调制方式为后沿调制，采样频率为开关频率的3倍，采样方式与第2节示例相同，控制器每个开关周期更新一次调制波，电流电压采样值送入观测器用于参数估计，子区间占空比ds按式（12）计算。观测器估算初值设置为C=190 μF，r=50 mΩ，R=1.5 Ω，L=1.2 mH，rL=10 mΩ。

为方便描述，将用式（2）作为预测方程的方法称为方法Ⅰ，用式（9）作为预测方法的方法称为方法Ⅱ。方法Ⅰ仿真辨识结果如图3所示。各项参数估计均表现出不同程度的误差，电容参数估计的误差尤为严重，这是由于低采样率时，输出电压的动力行为非线性程度较高，导致仿射非线性模型误差较大，而电感电流总是近似线性变化，仿射非线性模型能够对其行为有较好的描述，因此电感参数的估计较为准确。

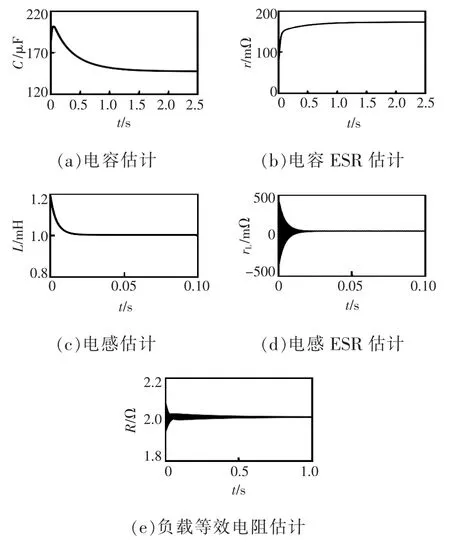
图3 方法Ⅰ的仿真结果Fig.3 Simulation results of methodⅠ

表1 Buck变换器仿真参数Tab.1 Simulation parameters of Buck converter

方法Ⅱ仿真辨识结果如图4和图5所示。图4为Lyapunov函数和随时间变化的曲线，由图可见，两者均随时间单调下降。参数估算结果如图5所示，由图可见，除电感电阻外均收敛到电路仿真设置值。由于电路模型中并未考虑开关管电阻，观测器估计的电感电阻收敛到55 mΩ为开关管导通电阻和电感电阻之和。参数辨识结果汇总在表2中。对比可知，加入模型噪声估计能很大程度的提高辨识精度，对于低采样率的在线辨识系统很有必要。

图4 Lyapunov函数变化曲线Fig.4 Variation of Lyapunov functions

图5 方法Ⅱ的仿真结果Fig.5 Simulation results of methodⅡ

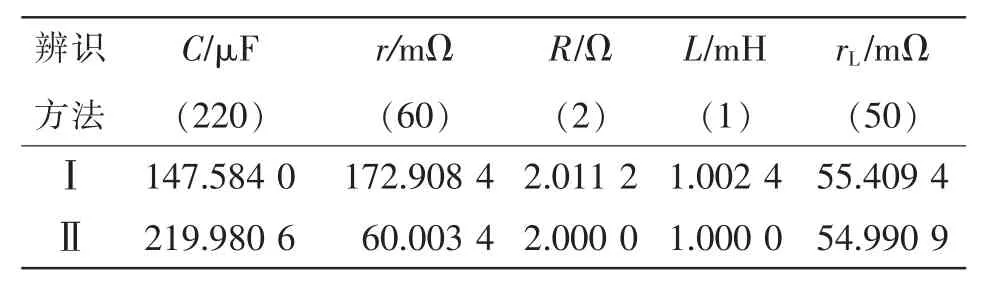
表2 参数辨识结果Tab.2 Simulation results of parameter estimation

5 实验结果与分析

为验证方法的有效性，制作了同步Buck变换器实验样机及其在线辨识系统，如图6所示，其输入电压为12 V，输出电压为2～9 V，开关频率为10 kHz。使用TH2818 LCR表在10 kHz频率下对主电路中输出母线电容、滤波电感、负载电阻进行了测量，测量结果如表3所示。其中电感ESR为直流电阻，这是由于电感ESR频率特性明显，而CCM下变换器中电感电流的直流分量远大于纹波分量，对被检测量造成影响的主要是电感的直流电阻。

图6 实验装置Fig.6 Experimental setup

实验采用Altera Cyclone IV现场可编程逻辑门阵列FPGA（field programmable gate array）控制同步Buck变换器，变换器采用后沿调制，FPGA控制AD转换器ADS8363对输出电压、输出电压纹波和电感电流进行同步采样，采样方式为第2节方式，采样频率为30 kHz。输出电压纹波由高通滤波器对母线电压滤波得到，当纹波较大可直接测量时该环节可以省略。将采样数据以及控制器输出送入NIOS II软核中的观测器进行参数在线辨识，观测器初值与第4节中仿真使用初值相同，观测器输出经窗口长为128的移动平均滤波器滤波作为辨识结果输出。占空比不同时的实验结果如表3所示。由表可知，实验结果与仿真一致，方法Ⅰ对电感参数和负载参数有较好的辨识结果，但无法有效地辨识电容参数，不能在采样率较低时使用；方法Ⅱ则克服了方法Ⅰ的缺点，能有效地对变换器电容、电感以及负载进行在线辨识。滤波电感ESR辨识值rL随着占空比d增大而增大，这是由于占空比增大，变换器输出功率增大，电源输出电压即变换器输入电压下降，而观测器认为该电压恒定。此外半桥上下管等效导通电阻不同也对此有影响。回路中其他部分如开关管、线路及传感器等的寄生电感和电阻对滤波电感及其ESR的辨识结果偏大有一定贡献。另外传感器、AD转换器等的测量误差、噪声干扰以及观测器数值计算误差对系统的辨识精度也有一定影响。

表3 Buck变换器参数辨识实验结果Tab.3 Experimental results of parameter estimation

6 结语

本文提出了一种新颖的基于观测器的DC/DC变换器主电路多参数在线辨识方法。该方法基于Lyapunov稳定性原理和离散系统模型，根据变换器输出电压、电感电流采样以及控制器输出对功率变换器主电路参数，如滤波电感、滤波电感ESR、滤波电容容值、滤波电容ESR和负载电阻等进行在线辨识，容易集成在控制器中。以Buck变换器为例介绍了所提出方法的设计和应用，并通过仿真和实验验证了方法的可行性。相对于传统的参数辨识方法，本方法能同时满足低采样率和不影响变换器运行的需求，由于离散建模方法和观测器算法的通用性，可较易推广到其他拓扑中。

［1］Yang Shaoyong，Xiang Dawei，Bryant A，et al.Condition monitoring for device reliability in power electronic converters：a review［J］．IEEE Transactions on Power Electronics，2010，25（11）：2734-2752．

［2］Wang Huai，Blaabjerg F．Reliability of capacitors for DC-link applications in power electronic converters-an over-view［J］．IEEE Transactions on Industry Applications，2014，50（5）：3569-3578．

［3］Lee D C，Lee K J，Seok J K，et al．Online capacitance estimation of DC-link electrolytic capacitors for three-phase AC/DC/AC PWM converters using recursive least squares method［J］．IEE Proceedings-Electric Power Applications，2005，152（6）：1503-1508．

［4］Abo-Khalil A G，Lee D C．DC-capacitance estimation of DC-link capacitors using ac voltage injection in AC/DC/AC PWM converters［C］.Conference Record of the 2006 IEEE Industry Applications Conference Forty-First IAS Annual Meeting．Tampa：IEEE，2006：2095-2100．

［5］Abo-Khalil A G，Lee D C．DC-link capacitance estimation in AC/DC/AC PWM converters using voltage injection［J］．IEEE Transactions on Industry Applications，2008，44（5）：1631-1637．

［6］Hannonen J，Honkanen J，Strom J P，et al．Capacitor aging detection in DC-DC converter output stage［C］.2015 IEEE Energy Conversion Congress and Exposition（ECCE）．Montreal：IEEE，2015：5538-5545．

［7］Aeloiza E C，Jang-Hwan K，Enjeti P N，et al．A real time method to estimate electrolytic capacitor condition in PWM adjustable speed drives and uninterruptible power supplies［C］.2005 IEEE 36th Power Electronics Specialists Conference．Recife：IEEE，2005：2867-2872．

［8］Imam A M.Condition monitoring of electrolytic capacitors for power electronics applications［D］．Georgia：Georgia Institute of Technology，2007．

［9］Imam A M，Divan D M，Harley R G，et al．Real-time condition monitoring of the electrolytic capacitors for power electronics applications［C］.APEC 07-Twenty-Second Annual IEEE Applied Power Electronics Conference and Exposition,Anaheim：IEEE，2007：1057-1061．

［10］Wiesinger T，Ertl H．A novel real time monitoring unit for pwm converter electrolytic capacitors［C］.2008 IEEE Power Electronics Specialists Conference,Rhodes：IEEE，2008：523-528．

［11］Buiatti G M，Martín-Ramos J A，García C H R，et al．An online and noninvasive technique for the condition monitoring of capacitors in boost converters［J］．IEEE Transactions on Instrumentation and Measurement，2010，59（8）：2134-2143．

［12］Abdennadher K，Venet P，Rojat G，et al．A real-time predictive-maintenance system of aluminum electrolytic capacitors used in uninterrupted power supplies［J］．IEEE Transactions on Industry Applications，2010，46（4）：1644-1652．

［13］Abdennadher K，Venet P，Rojat G，et al．Kalman filter used for on line monitoring and predictive maintenance system of aluminium electrolytic capacitors in UPS［C］. 2009 IEEE Energy Conversion Congress and Exposition．San Jose：IEEE，2009：3188-3193．

［14］Wechsler A，Mecrow B C，Atkinson D J，et al．Condition monitoring of DC-link capacitors in aerospace drives［J］．IEEE Transactions on Industry Applications，2012，48（6）：1866-1874．

［15］Yao Kai，Tang Weijie，Hu Wenbin，et al．A current-sensorless online ESR and C identification method for output capacitor of buck converter［J］．IEEE Transactions on Power Electronics，2015，30（12）：6993-7005．

［16］Yao Kai，Tang Weijie，Bi Xiaopeng，et al．An online monitoring scheme of DC-link capacitor's ESR and C for boost PFC converter［J］．IEEE Transactions on Power Electronics，2015，31（8）：5944-5951．

［17］Bordons C，Montero C．Basic principles of MPC for power converters：Bridging the gap between theory and practice［J］．IEEE Industrial Electronics Magazine，2015，9（3）：31-43．

［18］Vazquez S，Leon J I，Franquelo L G，et al．Model predictive control：A review of its applications in power electronics［J］．IEEE Industrial Electronics Magazine，2014，8（1）：16-31．

［19］Rodriguez J，Kazmierkowski M P，Espinoza J R，et al．State of the art of finite control set model predictive control in power electronics［J］．IEEE Transactions on Industrial Informatics，2013，9（2）：1003-1016．

［20］马皓，毛兴云，徐德鸿．基于混杂系统模型的DC/DC电力电子电路参数辨识［J］．中国电机工程学报，2005，25（10）：50-54．Ma Hao，Mao Xingyun,Xu Dehong.Parameter identification of DC/DC power electronic circuits based on hybrid system model［J］．Proceedings of the CSEE，2005，25（10）：50-54（in Chinese）.

［21］马皓，毛兴云，徐德鸿．兼顾电感电流连续导通和断续运行模式的 DC/DC电路建模和参数辨识［J］．中国电机工程学报，2006，26（5）：64-69．Ma Hao，Mao Xingyun，Xu Dehong．Modeling and parameter identification of DC/DC converters in both CCM and DCM mode［J］．Proceedings of the CSEE，2006，26（5）：64-69（in Chinese）．

［22］孙凤艳，王友仁，林华，等．基于频域建模与遗传算法的电力电子电路参数辨识方法［J］．电工技术学报，2011，26（11）：99-104．SunFengyan，WangYouren，LinHua，et al．Parameter identificationofpowerelectroniccircuitbasedontransferfunction modeland genetic algorithm［J］．Transactions of China ElectrotechnicalSociety，2011，26（11）：99-104（inChinese）．

［23］Al-Hosani K，Utkin V I．Parameters estimation using sliding mode observer with shift operator［J］．Journal of the Franklin Institute，2012，349（4）：1509-1525．

［24］Renaudineau H，Martin J P，Nahid-Mobarakeh B，et al．DC-DC converters dynamic modeling with state observerbased parameter estimation［J］．IEEE Transactions on Power Electronics，2015，30（6）：3356-3363．

［25］Li B X，Low K S．Low sampling rate online parameters monitoring of DC-DC converters for predictive-maintenance using biogeography-based optimization［J］．IEEE Transactions on Power Electronics，2016，31（4）：2870-2879．

Online Parameter Estimation of DC/DC Converters Based on Discrete-time Observer

WU Hangju,ZHOU Luowei
（State Key Laboratory of Power Transmission Equipment&System Security and New Technology, Chongqing University,Chongqing 400044,China）

A novel online parameter estimation approach for DC/DC converters is presented in this paper.The approach is realized using the proposed discrete-time observer algorithm based on Lyapunov functions.Introducing the model noise estimation makes the observer suitable for low sampling rate applications.To apply the proposed algorithm into DC/DC converter parameter estimations,a discrete-time model for converters is required.The modeling approach is introduced taking the Buck converter as an example,and the detailed observer design for Buck converters is also given. Based on the measured output voltage,inductor current and controller commands,the observer provides an estimate of the Buck converter circuit parameters.Simulation and experiment results are presented to validate the effectiveness of the proposed estimation method.

Buck converter;online parameter estimation;low sampling rate;online monitoring;parameter observer