基于二端口网络的三相逆变器传导共模EMI模型

2017-06-05周作坚裴雪军

电源学报 2017年3期

关键词：共模干扰源电感

周作坚，马俊，周武，裴雪军

（华中科技大学强电磁工程与新技术国家重点实验室，武汉430074）

基于二端口网络的三相逆变器传导共模EMI模型

周作坚，马俊，周武，裴雪军

（华中科技大学强电磁工程与新技术国家重点实验室，武汉430074）

以典型的三相四桥臂逆变器为对象，分析其输入侧和输出侧传导共模干扰路径。根据逆变器共模干扰回路的结构和特点，结合二端口理论提出一种逆变器共模EMI的预测模型。分析了该模型的物理意义，给出了模型中阻抗参数及独立电压源的测量计算方法。最后，改变逆变器的结构和运行工况后测量输入侧输出侧共模电流，预测结果和实验结果的对比验证了该模型的正确性。

逆变器；共模干扰；二端口理论；电磁干扰预测

随着电力电子技术的发展，采用脉冲宽度调制PWM（pulse width modulation）方式的逆变器被广泛应用于航海、航空、工业等多种对安全性要求很高的行业。但是随着开关频率的不断提高，由开关高速动作引起的电磁干扰EMI（electromagnetic interference）越来越严重，高频的电磁干扰不仅会影响自身的正常工作、缩短其使用寿命，而且对周围的其他设备的正常工作带来严重影响。

目前对逆变器系统电磁干扰的抑制方法主要是采用在传导路径增加无源滤波装置。逆变器系统传导EMI建模对无源滤波器设计具有重要意义。传统的时域建模方法需要对系统的杂散参数进行非常精确的提取，而这一过程非常困难并且无法精确到所有部件。时域模型自身的复杂和内部的非线性器件（如IGBT等开关器件）使传统的时域方法既耗时又很难达到较高的精确度［1］。

频域模型相对而言既快速又简单。早期的频域方法是在时域的基础上将干扰源和耦合路径转换得到相应的频域数学模型，再进行计算。文献［2］提出了运用双重傅里叶积分法来描述共模电压的数学模型，但因为这种对半导体器件建模的方法依然包含理想因素，所以其精确度并没有太大的提高；文献［3-5］将开关暂态波形简化成梯形波，这种近似的方法导致预测结果在高频段出现了较大误差。因此提出一种简单、精确且适用性广的方法变得很有必要。

本文通过对一台三相四桥臂逆变器系统的传导共模EMI的干扰源和传导路径进行分析，并结合二端口网络理论，得出基于二端口网络的三相逆变器共模EMI等效模型。最后，通过在直流侧加入共模电感和改变母线电压的方法，验证模型的正确性。

1 共模EMI二端口模型理论

典型的三相四桥臂逆变器系统拓扑结构如图1所示，图1中CPG和CNG分别是正、负母线对地的寄生共模电容，CMG是逆变器每个桥臂中点对地的寄生共模电容，C0是每个开关管上并联的寄生电容。该系统由线路阻抗稳定网络LISN（line impedance stabilization network）、逆变桥臂和输出LC滤波器组成。相比于传统的三相三桥臂逆变器系统，三相四桥臂的拓扑结构和调制方式更加复杂，如果使用传统的建模预测方法，工作量将大大增加，且无法得到足够的精度。从图可以看出电路结构具有如下特点：①正负母线LISN对称；②4个桥臂结构对称；③输出滤波器结构对称。这将有助于后面逆变器系统预测模型的建立。

图1 三相四桥臂逆变器系统结构Fig.1 Structure of three-phase four-leg inverter system

逆变器系统的逆变桥部分结构复杂，杂散参数众多且难以精确提取，而且开关器件开通关断过程是非线性的。这使得逆变桥部分的预测变得非常困难。但是预测的目的之一是为了指导设计EMI滤波器，设计EMI滤波器时并不关心逆变桥内部干扰信号的变化。所以，在进行预测时可以将逆变桥部分看成一个黑盒子，只需观察逆变桥输入输出端口的传导干扰信号。所以本文采用端口网络的思想对三相四桥臂逆变系统进行等效建模。

图2为采用端口思想对逆变系统进行等效后的模型。其中左边和右边的白色盒子分别代表图1中直流侧LISN和交流侧LC滤波器，黑盒子代表图1中虚线框内IGBT模块和直流侧支撑电容组成的逆变器系统主体部分。白盒子内部结构清晰、多变、易于测量，相对而言黑盒子内部结构复杂、固定、难于测量。在对称逆变系统中，根据电路结构特点可知直流侧正负母线PN上流过的共模电流大小相等，方向相同，同理，交流侧abcd四相也是如此。所以，逆变器系统可进一步简化得到如图3所示的端口等效模型。其中端口①代表正负母线短接后相对于地，端口②代表交流侧abcd四相短接后相对于地。

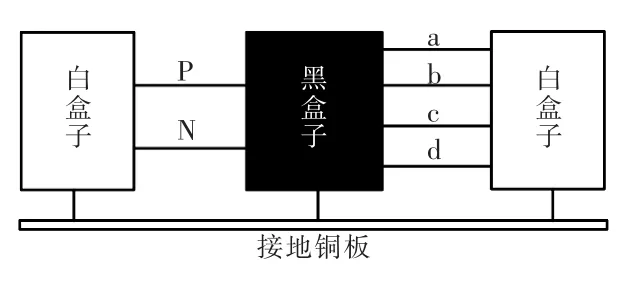
图2 基于端口网络的等效模型Fig.2Equivalent model based on port network

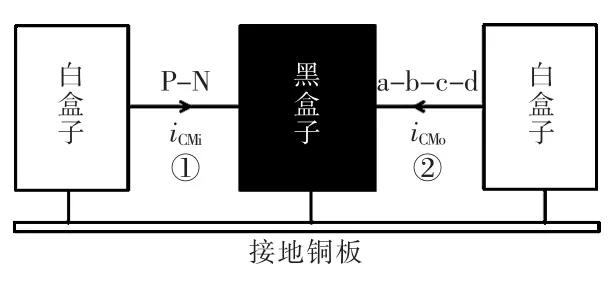
图3 简化的等效模型Fig.3 Equivalent model with further simplified

在经典电路理论中，当需要计算某复杂网络中的支路电压或者电流时，可以将该支路以外的其他部分视为一个一端口网络，并将一端口网络用最简单的等效电路来等效。推广之，如果计算复杂网络的2条不同支路的电压或者电流，可将网络的其他部分视为一个二端口网络。对端口的定义是要求从端口的一个端子流入网络的电流必须等于从另一个端子流出网络的电流。在经过端口等效之后的模型中，因为白盒子部分都是无源器件，所以黑盒子左侧及右侧流出和流入的共模电流大小相等。所以图3中的黑盒子变成了一个有源二端口网络，白盒子变成了无源一端口网络。根据电路理论中二端口网络理论，图3可以进一步等效得到如图4所示的共模EMI二端口模型。

图4 共模EMI二端口模型Fig.4 Two-port model of common-mode EMI

根据共模EMI二端口模型可得

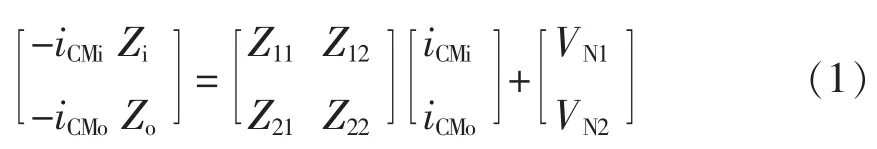
2 共模EMI二端口模型的建立

为了验证模型可行性，利用图4所示的模型来预测实验样机直流侧和交流侧共模电流。样机的拓扑如图1所示，样机的主要参数如下：直流母线电容为2 400 μF，由4个600 μF电容并联构成；交流滤波电感为1.1 mH，滤波电容为100 μF，交流侧滤波器的谐振频率为180 Hz，见表1。根据式（1）可知，为了计算出共模电流iCMi和iCMo，只需求出此时的阻抗矩阵Z、2个等效共模干扰源VN1、VN2和输入、输出侧阻抗Zi、Zo。

表1 逆变器样机工况参数Tab.1 Parameters of inverter prototype

2.1 模型阻抗矩阵参数Z的提取

共模EMI二端口模型中的各个参数都与逆变系统中的寄生参数相关，阻抗矩阵Z是无源二端口网络，可以通过分析断电模式下的电路结构求得。由此可以得出断电模式下逆变器主体部分在低频段的等效电路［6-7］，如图5所示。

图5 断电模式下逆变器主体近似等效模型Fig.5 Approximate CM equivalent circuit of the inverter under power-off condition

典型无源二端口网络如图6所示。根据其特性可知，阻抗矩阵Z的端口电压电流关系为

图6 典型无源二端口网络Fig.6 Typical passive two-port network

由于系统的对称性，假设Z12和Z21相等，那么根据式（2）可得

结合图5和式（3）～式（6）可得

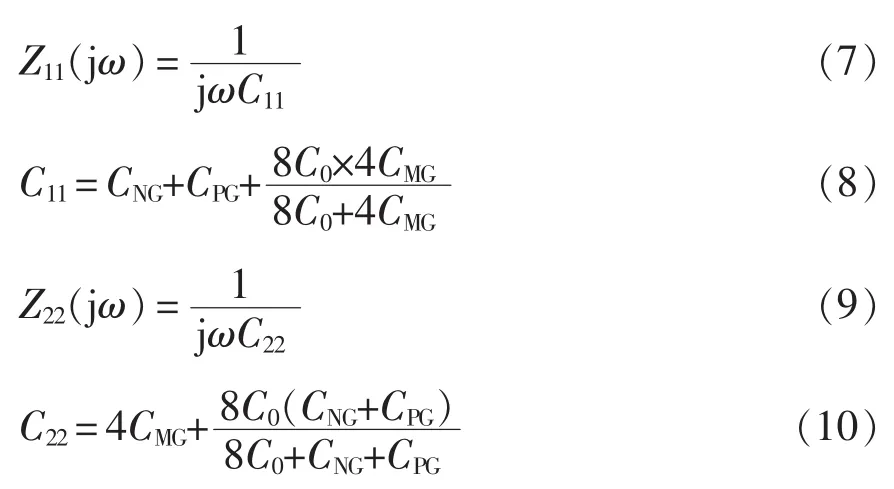
由文献［6］对逆变器主体部分低频段等效电路的分析，CPG、CNG、CMG约几十pF，C0约几百pF。根据上述寄生电容之间的关系可得出

上述分析表明，阻抗矩阵Z中的4个阻抗参数在低频段近似相等，呈现容性。但在高频段时，由于寄生电感的存在，这些阻抗会出现差异，呈现感性。

根据上述等效模型，把图1中虚线框内的逆变器主体部分从系统中剥离出来，同时将正负母线和交流侧四相分别短接得到的结构如图7所示。用阻抗分析仪测量［8～10］如下：将②号端口断开，测量端口①的等效端口阻抗；将①号端口断开，测量端口②号的等效端口阻抗；将②号端口短路，测量端口①的等效端口阻抗。

图7 阻抗矩阵测量模型Fig.7 Model of impedance matrix extraction

从式（3）～式（5）可知，以上3步测出的数据分别对应式中的 Z11、Z22和 ZSCM，再根据式（6）计算得到Z12和Z21。自此通过测量和计算得到阻抗矩阵Z（包括阻抗幅值和相位）。图8所示为阻抗矩阵Z的频谱。从阻抗矩阵频谱发现，等效阻抗在低频段呈现容性，在高频段呈现感性。4个阻抗频谱基本吻合，尤其是在低频段，这与理论计算的结果相符。

图8 阻抗矩阵Z频谱Fig.8 Spectrogram of impedance matrix Z

2.2 等效共模干扰源的提取

在提取等效共模干扰源VN1、VN2时，等效干扰源无法直接测量，本文采用间接测量和计算的方式提取等效干扰源。根据式（1）可推出

由式（15）可知，要得到干扰源那么需要得到等式右边的所有信息，其中阻抗矩阵Z已经通过前述方法测得。输入和输出侧阻抗Zi和Zo都是由一些无源器件组成，可以用阻抗分析仪直接测量得到精确的数据。此时采用和测量阻抗矩阵同样的处理方法，分别短路LISN连接的直流母线和LC滤波器连接的四相交流线，测量方法如图9和图10所示，测量得到输入输出侧阻抗频谱如图11所示。

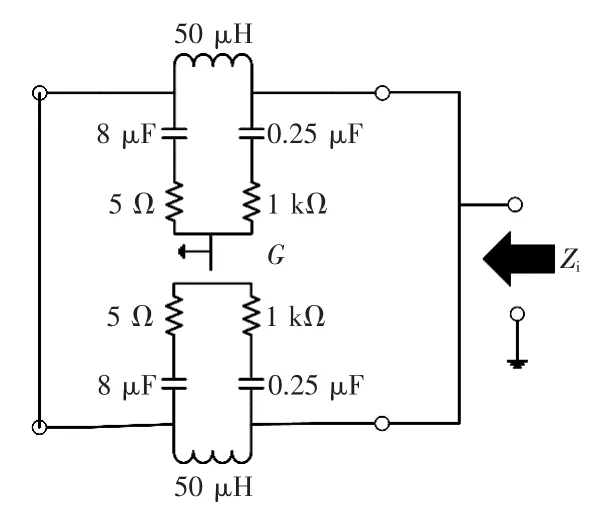
图9 输入侧阻抗Zi测量Fig.9 Measurement of input side impedance Zi

图10 输出侧阻抗Zo测量Fig.10 Measurement of output side impedance Zo

在提取用来计算等效干扰源VN1和VN1的共模电流iCMi和iCMo时，需要同时在直流侧和交流侧加入电流探头，测量同一时刻下的输入侧和输出侧的时域共模电流并用示波器记录下数据。通常情况下，共模干扰源重复在每个基波周期，所以此处采样一个基波周期20 ms进行分析，将得到的共模电流时域数据通过快速傅里叶变换FFT得到频域数据。实验用电流探头为力科CP150，带宽可达到10 MHz，频域预测的频段范围为10 kHz～10 MHz。将所有数据代入式（15）计算得出等效干扰源VN1和VN2的频域频谱，如图12所示。

图11 输入输出侧阻抗频谱Fig.11 Spectrogram of input and output side impedance

图12 等效干扰源VN1和VN2频谱Fig.12 Spectrogram of equivalent noise sources VN1and VN2

3 模型验证

常用的传导EMI抑制方法是在传导路径上增加无源滤波装置，图1中的逆变器系统直流侧没有加入任何共模滤波器。如果需要得到加入一个特性已知的共模电感后的抑制效果，费时、费力、高成本的做法就是制作实物滤波器并加入系统中，然后通过实验测量观测直流侧的共模电流。此时，EMI预测模型的优势就非常突出，它能够快速简单展示出加入该滤波器后EMI的抑制效果，极大地方便EMI滤波器的设计与整改。

前文中已经通过实验和计算的方法得到图1逆变器系统的阻抗和干扰源参数。现将一个已知阻抗特性的共模电感加入直流侧，但不改变其他运行工况，加入后的结构如图13所示。此时虚线框内的逆变桥部分并没有变化，说明加入共模电感后阻抗矩阵Z并没有变化。同理，等效干扰源是由虚线框内的主体部分决定，影响因素包括母线电压、开关器件、调制方式等，而这些因素也与直流侧的共模电感无关，所以加入共模电感后等效干扰源VN1和VN2也没有发生变化。这两个不变因素是做预测工作的重要前提。

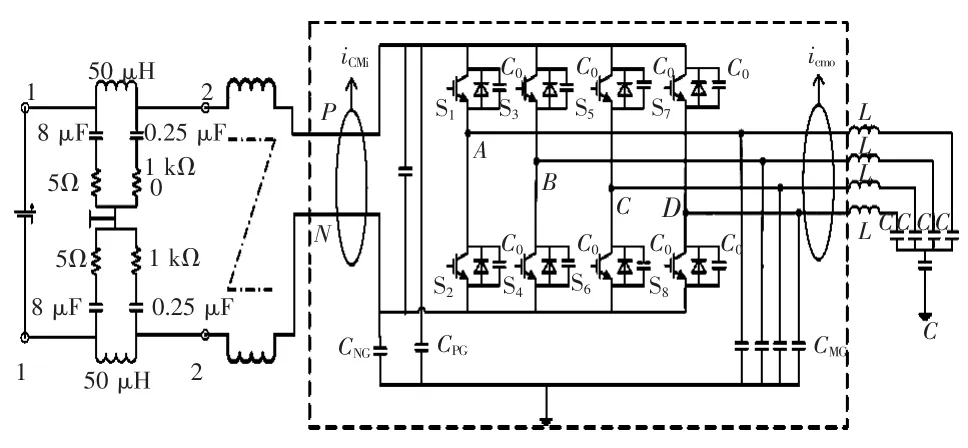
图13 直流加入共模电感后的逆变系统Fig.13 Structure of inverter with CM（common-mode）inductor inserted at dc-side

加入共模电感后，只有输入侧阻抗Zi产生变化，输出侧阻抗Zo未变。由于共模电感的阻抗特性已知，结合第2节中测量输入侧阻抗的方法可迅速得到新的输入侧阻抗。图14所示为加入共模电感前后输入侧阻抗频谱对比。

图14 加共模电感前后输入侧阻抗对比Fig.14 Comparison of impendence of input-side with and without CM inductor inserted

由式（1）可得

将阻抗矩阵Z、等效干扰源VN1、VN2和加共模电感后的输入、输出侧阻抗Zi、Zo代入式（16）中，即可计算得到加入共模电感后直流侧和交流侧共模电流的预测值，用示波器测量加入共模电感后的直流侧和交流侧共模电流，转化到频域后，将实测值与预测值进行比较，结果如图15所示。

从图中可以发现，在10 kHz～10 MHz内，预测共模电流频谱和实测共模电流频谱基本拟合，除了少数点误差较大，大部分误差控制在5 dB以内。预测误差的产生有多种原因，包括以下几点：被测量的噪声电流都非常小，测量数据有稍微的误差就会对预测结果产生较大的影响，所以测量设备的精度非常重要；在阻抗测量过程中，忽略了测试导线阻抗和一些无法测量的杂散参数的影响；测试所使用的阻抗分析仪存在测量范围，对超出范围的部分精度不足；在加入共模电感后，对开关管的开通关断过程电压电流有少许影响，从而导致干扰源也会有少许变化。

图15 加共模电感后共模电流实验值与预测值对比Fig.15 Comparison of measured and predicted CM currents with CM inductor

通过观察式（16）中的第1个等式，容易发现当在直流侧加共模电感后，仅仅只有分式的分母发生了变化，并由此引起了直流侧共模电流的变化。图16为组成分母的综合阻抗和直流侧共模电流在加共模电感前后的实验对比。显然加入共模电感后，组成分母的综合阻抗在150 kHz～1MHz有明显的上升，而直流侧共模电流在该频段有明显的下降。这说明在直流侧共模传导路径增加合适的共模滤波器能准确地抑制某一频段的共模干扰。这也为系统设计共模滤波器提供了参考。

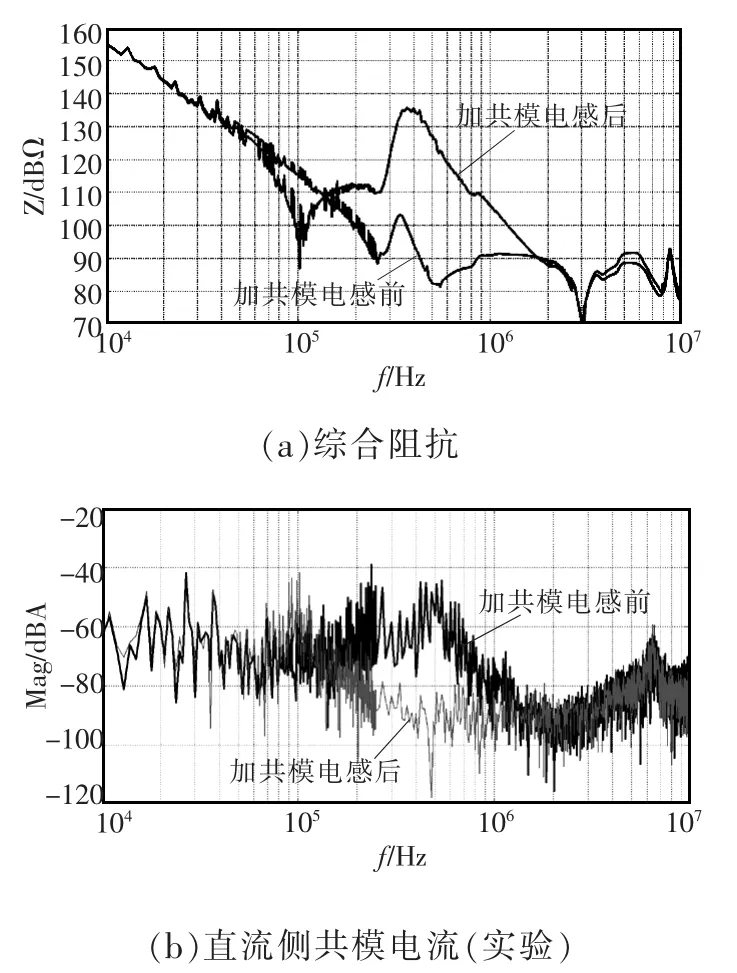
图16 加共模电感前后综合阻抗和直流侧共模电流对比Fig.16 Comparison of integrated impedance and measured input-side CM currents with and without CM inductor

上文中提到一个重要前提就是在直流侧加入共模电感并不会影响等效干扰源VN1和VN2，那么在加共模电感前后等效干扰源频谱图应该重合，图17所示为加共模电感前后等效干扰源的频谱图，通过对比发现，两条曲线基本吻合，由此验证该前提是有效的。

母线电压是影响等效干扰源的几个重要因素之一。当其他工况不变时，直流侧由于隔直电容的存在其等效干扰源与母线电压成正比，即

为了验证上述结论，测量加共模电感后在母线电压分别为200 V、300 V、400 V（实验样机运行在母线电压低于600 V时其调制比不变，即调制方式不变）时的直流侧和交流侧共模电流。用300 V时的共模电流计算得出相应的等效干扰源VN1_300和VN2_300，再结合已知的阻抗信息，由式（16）可计算出此时200 V、400 V时的共模电流，并与实验数据对比，结果如图18所示。从对比结果中可以看出，预测值和实测值在整个频段内除少数几个频率点外，误差都在5 dB内，验证了等效干扰源和母线电压之间的关系，也验证了该模型EMI预测的正确性和有效性。

图17 加共模电感前后等效干扰源对比Fig.17 Comparison of equivalent noise sources VN1and VN2with and without CM inductor inserted

图18 不同母线电压下共模电流预测与实验结果对比Fig.18 Comparison of CM currents with different dc input voltages

4 结语

为了克服传统EMI预测模型的局限性，本文提出了一种基于二端口网络理论共模EMI等效模型，该模型用1个阻抗矩阵和2个等效干扰源来模拟逆变系统输入输出的端口特性。该模型成功地预测了增加共模滤波器后逆变系统的共模电流，同时也验证了在其他工况不变的情况下，共模电流与母线电压成比例的结论。

基于二端口理论的逆变器共模EMI模型能够快速评估出共模滤波器对共模干扰的抑制效果，可适用于多种结构对称的逆变系统，如三相四桥臂逆变器、多电平逆变器等。该模型也对共模EMI滤波器的设计具有重要的指导意义。

［1］孟金磊,宁圃奇,温旭辉,等.一种有限差分IGBT/FWD模型研究［J］.电源学报,2015,13（4）：46-52. Meng Jinlei,Ning Puqi,Wen Xuhui,et al.A finite differential method based IGBT/FWD model in PSPICE［J］. Journal of Power Supply,2015,13（4）：46-52（in Chinese）.

［2］Holmes D G.A general analytical method for determiningthe theoretical harmonic components of carrier based PWM strategies［C］.In Industry Applications Conference,1998. Thirty-Third IAS Annual Meeting.The 1998 IEEE.,1998.

［3］Ran L,Gokani S,Clare J,et al.Conducted electromagnetic emissions in induction motor drive systems.II.Frequency domain models［J］.IEEE Trans.Power Electron.,1998,13：768-776.

［4］Pei Xuejun,Zhang Kai,Kang Yong,et al.Analytical estimation of common mode conducted EMI in PWM inverter［C］.Conf.Rec.IEEE IAS Annu.Meeting,2004,4：2651-2656.

［5］Revol B,Roudet J,Schanen J L,et al.EMI study of threephase inverter-fed motor drives［J］.IEEE Trans.Ind.Appl., 2011,47（1）：223-231.

［6］Tao Qi,Graham J,Sun Jian.Characterization of IGBT modules forsystem EMI simulation［C］.Proc.25th Appl.Power Electron.Conf.Exp.,Feb.21-25,2010：2220-2225.

［7］Kang X,Santi E,Hudgins J L,et al.Parameter extraction for a physics-based circuitsimulator IGBT model［C］.Procedings of IEEE APEC’03,2003：946-952.

［8］Jettanasen C,Costa F,Vollaire C.Common-mode emissions measurement sand simulation in variable-speed drive systems［J］.IEEE Trans.Power Electron.,2009,24（11）：2456-2464.

［9］Costa F,Vollaire C,Meuret R.Modeling of conducted common mode perturbations in variable-speed drive systems［J］.IEEE Trans.Electromagn.Compat.,2005,47（4）：1012-1021.

［10］Wang Ruxi,Blanchette H F,Boroyevich D,et al.EMI noise attenuation prediction with mask impedance in motor drive system［C］.Applied Power Electronics Conference and Exposition（APEC）,2012 Twenty-Seventh Annual IEEE,2012：2279-2284.

Conducted Common-mode EMI Model Based on Two-port Network for Three-phase Inverter

ZHOU Zuojian,MA Jun,ZHOU Wu,PEI Xuejun
（State Key Laboratory of Advanced Electromagnetic Engineering and Technology,Huazhong University of Science and Technology,Wuhan 430074,China）

A typical three-phase four-leg inverter is studied in order to investigate the conducted common-mode electromagnetic interference（EMI）loop at both the input and output sides of the inverter.A common-mode EMI model of the inverter based on the two-port theory is proposed according to the structure and characteristics of its common-mode interference loop.The physical definition of the model is analyzed.the method of the model parameters extraction and calculation is given out.Finally,the input and output side common-mode current is measured after changing the structure and operating condition of the inverter.The model is verified by the comparison between the prediction results and the experimental results.

inverter;common-mode EMI;two-port theory;EMI prediction