马尾松宏观尺度单木生长模型研究

刘四海,曾伟生

(1.湖北省崇阳县国营桂花林场,湖北 崇阳 437524；2.国家林业局调查规划设计院,北京 100714)

马尾松宏观尺度单木生长模型研究

刘四海1,曾伟生2

(1.湖北省崇阳县国营桂花林场,湖北 崇阳 437524；2.国家林业局调查规划设计院,北京 100714)

林木生长模型是预测森林未来发展、评估生产潜力的定量依据。以我国南方主要针叶树种马尾松(Pinusmassoniana)为对象,利用在马尾松分布范围内收集的代表性样本,建立全国尺度的胸径和树高单木生长模型,并分析生长模型是否受地域和起源的影响。结果表明:马尾松胸径的生长过程仅与地域有关而与起源无关,而树高的生长过程则受到地域和起源的双重影响；所建胸径和树高总体平均生长模型,确定系数分别为0.79和0.71,平均预估精度均在96%以上；包含地域和起源因子的胸径和树高生长模型,比总体平均模型有显著改进,其确定系数分别达到0.83和0.74,平均预估精度均进一步提高。所建生长模型为在宏观尺度上预测马尾松林的蓄积量、生物量和碳储量提供了定量参考依据。

马尾松;生长模型；Logistic函数；哑变量；地域；起源

单木生长模型是指用来描述单株林木生长过程的模型。依据是否含有林木间的相对位置因子,单木生长模型分为与距离无关和与距离有关两类[1]。单木生长模型是最基础的模型,与林分和径阶生长模型相比,其适用性更广[2]。21世纪以来,我国已有学者对马尾松(Pinusmassoniana)、落叶松(Larixspp.)、辽东栎(Quercusliaotungensis)、福建柏(Fokieniahodginsii)、水曲柳(Fraxinusmandschurica)等树种的单木生长模型进行研究[3-12],其研究的重点主要集中在如何选择合理的竞争指标,以及应用不同的方法来构建竞争指标和拟合模型参数。近年来,也有人尝试将单木生长模型与林分生长模型进行耦合[13]。综合来看,目前关于单木生长模型的研究,几乎都是往微观方向不断深入,试图寻找与林木生长有关的各种林木因子、林分因子以及立地、土壤等因子,以期所建生长模型能更准确反映研究地区的林木生长状况。但这种微观尺度的模型,其推广适用性就会受到限制。本文以我国南方的重要针叶树种马尾松为研究对象,试图从宏观尺度建立单木生长模型。主要研究目标包括:1) 利用常用的生长函数建立以全国为总体的平均生长模型,并选定最优生长函数作为进一步研究的基础模型；2) 利用哑变量建模方法建立含地域和起源因子的单木生长模型,分析按不同地域和起源建模是否能显著提高模型的预估精度；3) 按最优建模方案建立不同地域和起源的直径和树高生长模型,为全国和省域尺度预测马尾松的单木生长量提供依据,也为预测马尾松林的蓄积量、生物量和碳储量提供参考。

1 数据与方法

1.1 数据采集

马尾松广泛分布于我国长江流域的10多个省份。根据第八次全国森林资源清查结果,马尾松林面积1 001万hm2,蓄积5.91亿m3[14]。本文所用数据来自国家森林资源连续清查生物量调查建模项目组。根据《立木材积表》[15],马尾松二元材积表分两个地理区域范围编制,也称建模总体。总体1的地域范围包括湖南、江西、广东、广西、福建、浙江、江苏、安徽、贵州等省区,总体2的地域范围包括四川、重庆、湖北3省市。项目组收集的建模数据涉及两个总体:总体1包括147株样木的胸径、树高和年龄实测数据,其中,74株来自天然林,73株来自人工林；总体2包括151株样木的胸径、树高和年龄实测数据,其中,87株来自天然林,64株来自人工林。样本在马尾松的两个总体分布范围内具有广泛的代表性。表1给出了马尾松两个建模总体的样本统计特征值。

表1 马尾松两个建模总体的样本统计特征值

1.2 模型建立

1.2.1 基本模型的确定

已经发表的生长模型很多,本研究选用以下6个生长函数[12,16-17]:

Logistic函数:

y=a/(1+b×exp(-c×t))+ε

(1)

Richards函数:

y=a×(1-exp(-b×t))c+ε

(2)

Gompertz函数:

y=a×exp(-b×exp(-c×t))+ε

(3)

Schumacher函数:

y=a×exp(-b/(c+t))+ε

(4)

Mitscherlich函数:

y=a×(1-b×exp(-c×t))+ε

(5)

抛物线函数:

y=a+b×t+b×t2+ε

(6)

式中:y为林木胸径(D,cm)或树高(H,m)；t为林木年龄；a,b,c为模型参数；ε为误差项,假定其服从正态分布。

因为胸径和树高数据无明显异方差性,在参数估计时采取普通最小二乘法。上述6个生长函数中,前4个具有极值和拐点,为典型的“S”形曲线；Mitscherlich函数有极值无拐点；抛物线函数也有极值,但与前面5个函数的收敛极值不一样,抛物线有1个极值点,超过这个极值所对应的年龄后,函数的估计值又会逐渐下降,故在实践中,一般人为规定大于该年龄后树高保持极大值不变。根据对以上6个模型的拟合结果,在综合分析基础上,可以选定其中效果最好的模型,作为本研究的基础模型。

1.2.2 含地域和起源因子的生长模型

为了分析不同地理区域(建模总体)和起源对林木胸径和树高生长的影响,在确定基础模型后,引入2个哑变量(I和J)。当样木属于总体1的地域范围时,I=1,属于总体2的地域范围时,I=0；当样木来自天然林时,J=1,来自人工林时,J=0。以(1)式为例,含地域和起源因子的生长模型表述如下:

y=(a+a1I+a2J)/(1+(b+b1I+b2J)× exp(-(c+c1I+c2J)×t))+ε

(7)

式中:a1,a2,b1,b2,c1,c2为哑变量I和J的待估参数,其它字母含义同前。

如果反映地域和起源影响的部分参数在统计上与0无显著差异(变动系数大于50%),则将其从模型中剔除[17]。

1.3 模型评价

用于评价回归模型统计指标很多[6,8-9,13,17]。根据曾伟生等[18]对立木生物量模型的专题研究结果,评价模型的基本统计指标有6项,即确定系数(R2)、估计值的标准误(SEE)、平均预估误差(MPE)、总体相对误差(TRE)、平均系统误差(ASE)和平均百分标准误差(MPSE)。这些指标既适用于对立木生物量模型的评价,也适用于其它林业数学模型。本研究对单木生长模型的评价,也采用这6项指标,其计算公式[18]如下:

(8)

(9)

(10)

(11)

(12)

(13)

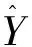
根据建立回归模型的传统做法,模型建立之后一般应利用检验样本进行适用性检验。然而,已有统计学家对模型适用性检验的理论和方法提出质疑[19-20],认为利用独立样本进行交叉检验,不能对模型评价提供额外的信息。因此,本文未开展交叉检验,而是利用全部样本数据进行建模,并用(8)—(13)式的统计指标对模型进行评价。

另外,为分析包含地域和起源因子的生长模型与不含地域和起源因子的模型之间是否存在显著差异,采用了F检验方法。F统计量计算公式[21-22]为:

(14)

式中:SSE2和SSE1分别为不含地域和起源因子与包含地域和起源因子生长模型的残差平方和,而df2和df1分别为不含地域和起源因子与包含地域和起源因子模型的自由度。

利用(14)式计算的F值与自由度分别为df2-df1和df1的F临界值进行比较,以确定两个模型之间是否存在显著差异。

2 结果与分析

2.1 总体平均生长模型

利用马尾松两个总体的全部样本数据,通过ForStat软件中的“非线性回归”方法,拟合(1)—(6)式。表2列出了6个生长模型的参数估计值及模型的确定系数R2。从表2知,不论是胸径生长模型还是树高生长模型,都是(1)式最好,(3)式次之,(5)式最差。因此,选定(1)式即Logistic生长函数作为最优模型,其胸径和树高生长模型的拐点年龄(连年生长率最大的年龄)分别为24a和19a。胸径生长模型的6项统计指标分别为:R2=0.7947,SEE=5.36cm,TRE=0.12%,ASE=0.40%,MPE=3.74%,MPSE=30.34%。树高生长模型的6项统计指标分别为:R2=0.7145,SEE=3.86m,TRE=0.02%,ASE=-0.09%,MPE=3.64%,MPSE=28.26%。可以看出,TRE和ASE两项指标均趋近于0,而MPE均小于4%,说明平均预估精度在96%以上,效果是很好的。另,从MPSE指标大小,可知生长曲线的变动范围或上下限区间,其上限和下限可视为最乐观和最保守的预测值。图1和图2给出了马尾松胸径和树高总体平均生长模型的拟合曲线及其上下区间。

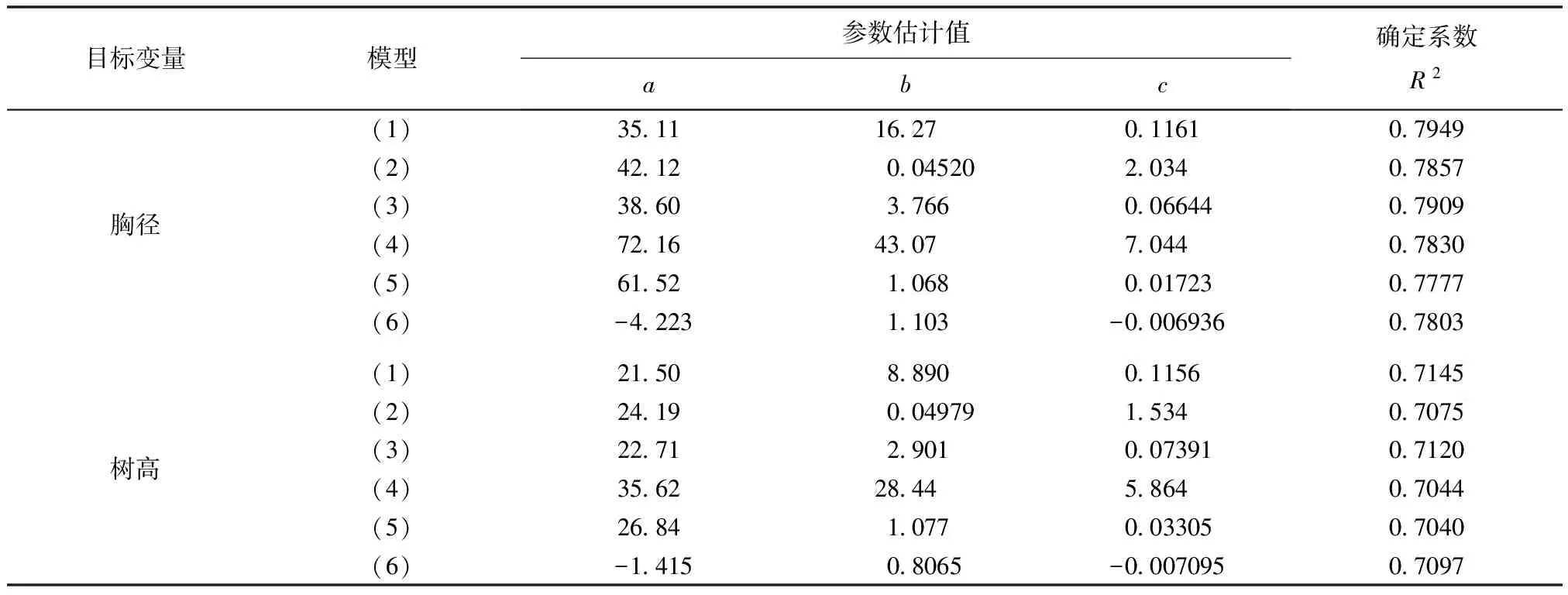
表2 马尾松6个总体平均生长模型的参数估计值及确定系数

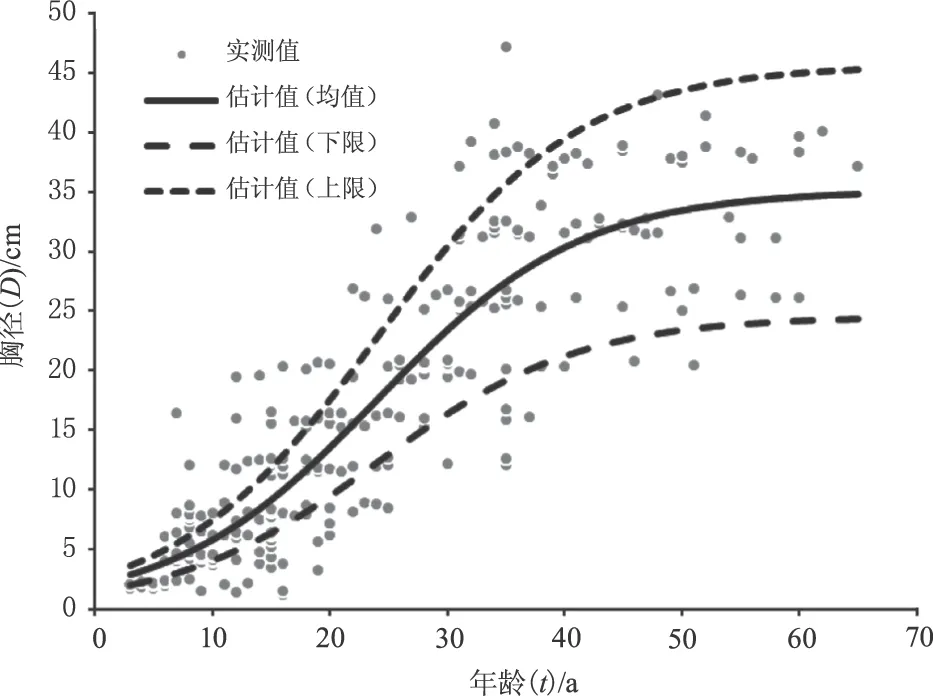
图1 马尾松胸径总体平均生长模型

图2 马尾松树高总体平均生长模型

2.2 含地域和起源因子的生长模型

利用马尾松含地域和起源因子的全部样本数据,利用“非线性回归”方法拟合(7)式。表3列出了2个含地域和起源因子生长模型的参数估计值及模型的统计指标,其中胸径模型仅含地域因子,且仅影响参数c；树高模型含地域和起源双因子,除地域影响参数c外,起源同时对参数a和c产生影响。按照(14)式可算出含地域和起源因子的胸径和树高生长模型与总体平均模型之间的F值分别为61.31和9.59,均高于其相应的临界值,说明模型之间差异显著。

根据表3的结果,可以得出总体1和总体2的胸径生长模型及各总体不同起源的树高生长模型,其模型参数、拐点年龄及统计指标如表4所示。胸径和树高生长模型的拟合效果分别如图3和图4所示。

表3 含地域和起源因子生长模型的参数估计值及统计指标

注：参数a1,b1,b2在统计上均与0无显著差异,已从模型中剔除。

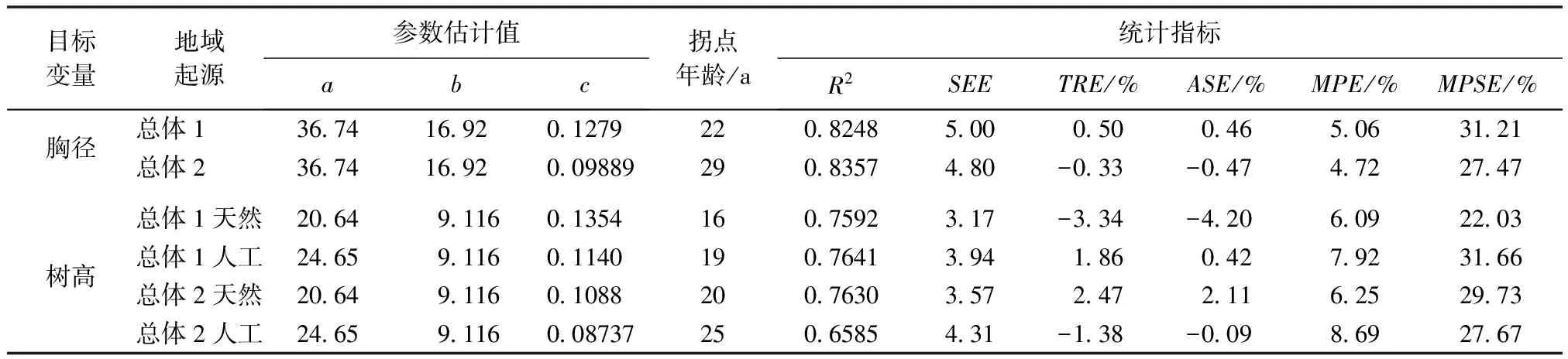
表4 不同地域和起源生长模型的参数估计值及统计指标

图3 马尾松胸径生长模型

图4 马尾松树高生长模型

从地域和起源对林木生长影响的分析结果看,马尾松胸径的生长过程仅与地域有关而与起源无关,而树高的生长过程则受到地域和起源的双重影响。就胸径生长而言,总体1的生长速度要快于总体2,这与两个总体的水热条件是相关的,因为总体1的地域范围位于长江流域东南部,水热条件较好；而总体2的地域范围位于长江流域的中西部,水热条件要差一些。就树高生长来看,总体1的生长速度也要快于总体2,这一点与胸径生长类似；另外,人工林的生长潜力要大于天然林,这一点既可从表4中极值参数a的大小和拐点年龄体现出来,也能从图4中预估曲线的对比上反映出来。究其原因,可能是现有马尾松人工林的立地条件要好于天然林,但还有待于进一步研究证实。

3 结论

本文利用在马尾松分布范围内收集的代表性样本,建立了全国尺度的胸径和树高生长模型,其确定系数分别为0.79和0.71,平均预估精度均在96%以上。因为各地马尾松的自然环境条件差异很大,不论是胸径生长还是树高生长,都存在±30%左右的变动。包含地域和起源因子的胸径和树高生长模型,比全国尺度的总体平均模型有显著改进,其确定系数分别达到0.83和0.74,平均预估精度均进一步提高。所建生长模型为在宏观尺度上预测马尾松林的蓄积量、生物量和碳储量提供了定量参考依据。

[1]任瑞娟,亢新刚,杨华.天然林单木生长模型研究进展[J].西北林学院学报,2008,23(6):203-206.

[2]邓成,吕勇,雷渊才,等.林木生长和收获模型研究进展与发展趋势[J].林业调查规划,2010,35(1):7-11.

[3]林成来,洪伟,吴承祯,等.马尾松人工林生长模型的研究[J].福建林学院学报,2000,20(3):227-230.

[4]刘兆刚,李凤日,于金成.落叶松人工林单木模型的研究[J].植物研究,2003,23(2):237-244.

[5]王文斗,李凤日,那冬晨,等.辽东栎单木生长模型的研究[J].林业科技,2005,30(2):11-13.

[6]张惠光.福建柏单木生长模型的研究[J].中南林业调查规划,2006,25(3):1-4.

[7]刘微,李凤日.落叶松人工林与距离无关的单木模型[J].东北林业大学学报,2010,38(5):24-27.

[8]卢海涛,李凤日,贾炜玮.水曲柳单木生长模型的研究[J].森林工程,2011,27(3):5-8.

[9]邓成,吕勇,雷渊才,等.以相对直径为竞争指标的单木直径生长模型研究[J].林业资源管理,2011(1):40-43.

[10]于士涛.塞罕坝华北落叶松生长模型的研究[J].河北林果研究,2012,27(1):1-5.

[11]姜立春,杜书立.基于非线性混合模型的东北兴安落叶松树高和直径生长模拟[J].林业科学研究,2012,25(1):11-16.

[12]何云松,陈亚文,林勇.重庆市石宝镇马尾松单木生长模型研究[J].四川林业科技,2013,34(5):56-60.

[13]高东启,邓华锋,蒋益,等.单木生长模型与林分生长模型耦合的方法——以油松为例[J].江西农业大学学报,2014,36(6):1298-1304.

[14]国家林业局.中国森林资源报告(2009—2013)[M].北京:中国林业出版社,2014.

[15]LY/T 1353-1999,立木材积表 [S].北京:中国标准出版社,1999.

[16]中华人民共和国林业部.林业专业调查主要技术规定[M].北京:中国林业出版社,1990.

[17]骆期邦,曾伟生,贺东北.林业数表模型——理论、方法与实践[M].长沙:湖南科学技术出版社,2001.

[18]曾伟生,唐守正.立木生物量模型的优度评价和精度分析[J].林业科学,2011,47(11):106-113.

[19]Picard R R,Cook R D.Cross-validation of regression models[J].J Am Stat Assoc,1984,79:575-583.

[20]Kozak A,Kozak R.Does cross validation provide additional information in the evaluation of regression models? [J].Canadian Journal of Forest Research,2003,33(6):976-987.

[21]Meng Shawn X,Huang Shongming,Lieffers V J,et al.Wind speed and crown class influence the height-diameter relationship of lodgepole pine:nonlinear mixed effects modeling[J].Forest Ecology and Management,2008,256(4):570-577.

[22]Zeng Weisheng,Zhang Huiru,Tang Shouzheng.Using the dummy variable model approach to construct compatible single-tree biomass equations at different scales—a case study for Masson pine (Pinus massoniana) in southern China[J].Canadian Journal of Forest Research,2011,41(7):1547-1554.

Large-scale Individual Tree Growth Models forPinusmassonianain China

LIU Sihai1,ZENG Weisheng2

(1.GuihuaStateForestFarmofChongyangCounty,Chongyang437524Hubei,China;2.AcademyofForestInventoryandPlanning,SFA,Beijing100714,China)

Individual tree growth models are quantitative basis for predicting forest development and evaluating productivity potential in the future.Based on the mensuration data of sample trees of Masson pine (Pinusmassoniana) in southern China,individual tree diameter and height growth models on national level were developed,and effects of region and origin on growth models were analyzed.The results showed that diameter growth model of Masson pine was only related to region,whereas height growth model was affected by both region and origin;coefficients of determination (R2) of the developed population average (PA) diameter and height growth models were 0.79 and 0.71 respectively,and mean prediction precisions were more than 96%;R2of the diameter and height growth models with region and origin in variables were 0.83 and 0.74 respectively,and mean prediction precisions were all improved,indicating that the models were significantly better than the PA models.The growth models developed in this study could provide quantitative basis for forecasting stock volume,biomass and carbon storage of Masson pine forest on large scale.

Pinusmassoniana,growth model,Logistic function,dummy variable,region,origin

2017-02-05；

2017-03-24

国家自然科学基金项目(31370634)

刘四海(1964-)，男，湖北崇阳人，工程师，主要从事林业生产与森林经营工作。Email：1694280017@qq.com

曾伟生(1966-)，教授级高工，博士，主要从事森林资源调查监测与林业数表研制工作。 Email：zengweisheng@afip.com.cn

S791.248

A

1002-6622(2017)02-0028-06

10.13466/j.cnki.lyzygl.2017.02.006