水平管油气两相段塞流及其传热特性

王鑫，王兆婷，张晓凌，何利民



水平管油气两相段塞流及其传热特性

王鑫，王兆婷，张晓凌，何利民

（中国石油大学（华东）储运系，山东省油气储运安全省级重点实验室，山东青岛266580）

海底油气管道的冷却传热过程是结蜡、水合物等海洋石油工业流动保障问题的关键控制因素。采用电容探针与热电偶、热电阻等流动及温度测量手段对不同冷却条件下空气-油段塞流的流动参数和传热参数进行实验测量，分析了空气-油段塞流流动参数对传热特性的影响，并与空气-水对流换热进行对比。结果表明，空气-油段塞流对流传热系数主要受液相折算速度的影响，且冷却液温度越低，管底热流体黏度越大，导致热边界层越厚，传热系数降低；受黏性力及边界层影响，对流传热系数远小于空气-水；沿管壁周向，从管顶到管底的对流传热系数不断增大。提出了适用于冷却条件下的油气段塞流传热关联式和传热模型。

气液两相流；传热；多相流；冷却条件；段塞流

引 言

在海底石油生产过程中，气-油段塞流是一种常见流型。油井产出物与周围海水环境的温差可导致管内水合物生成、蜡质析出，从而使管道流通面积减小，严重时甚至会堵塞管道，使油气生产中断[1]。掌握两相流传热机理，准确预测流动温度分布是保证油田安全生产的关键。

一些研究者对加热工况下段塞流的特性进行了实验研究，Oliver等[2]、Ghajar等[3-6]通过研究发现对流传热系数的增大源自于液相速度的提高，随气相流速的增大，对流传热系数有所增加但作用不明显。Oliver等[2]认为影响两相流换热的因素很多，但主要因素为液塞长度。

Ravipudi等[7-15]通过研究加热工况下两相流动的对流换热机理，提出基于Sieder-Tate关联式的两相对流传热系数关联式，但这些关联式没有区分流型，精度不高。Dukler等[16]通过对液塞体、长气泡以及液膜区的对流传热系数的加权平均得到用于计算段塞流平均对流传热系数的模型，但该模型没有考虑到气相的加入对换热效果的影响。Shah[17]以Froude数为辨别流型的参数，提出了适用于不同流型的关联式。Kago等[18]着重研究加热条件下水平管段塞流对流换热并提出了与Shah类似的关联式。Manabe[19]进行了水平管内原油-天然气冷却换热实验研究，针对间歇流、环状流建立了传热模型。Franca等[20]发现水平管内仅有少数气液两相对流传热系数关联式明确适用于段塞流型。Noville等[21]通过实验研究了不同热流体温度、不同冷却液温度下段塞流对流换热特性。

综上所述，气液两相流动对换热有重要影响。但冷却条件下以油气为介质的段塞流换热特性的研究报道较少，导致大部分两相流传热关联式对于海洋石油工业常见的段塞流型适应性较差。本文通过空气-油实验系统，开发了油气段塞流电容测量技术，利用电容电极互相关法获得了冷却条件下空气-油段塞流的流动特征参数，分析了气液相折算流速等参数对段塞流对流换热的影响，对比了空气-油对流换热与空气-水对流换热的不同，并分析了管壁周向不同位置处对流传热系数的分布情况。此外，本文将空气-油段塞流实验对流传热系数与3种关联式进行了对比，提出了适用于冷却条件下的油气段塞流传热关联式和段塞流流型的传热模型。

1 实验装置及数据分析方法

图1为实验采用的两相流循环管道示意图。该系统包括液相循环系统、气相循环系统、两相混合循环系统、液相加热系统、气相加热系统及冷却液循环系统，详细结构见文献[22]。在该实验装置上以空气-水为介质的段塞流传热的研究验证了该系统的可靠性[23]。

图2为互相关法电极组安装示意图。将两组电容电极安装在流动观察段，具体调试过程及原理详见文献[24-25]。互相关法的原理是，两列信号经互相关函数计算，得到R，其最大值对应的横坐标与纵轴之间的距离就是两列信号之间的延迟D，若上下游电容探针间的距离为D，则液塞速度s=DD。互相关函数表示为

计算出液塞速度后，根据电容探针测得的段塞流流动信号，可得到液塞及长气泡经过探针的时间长度，进而计算出液塞长度、液塞单元长度、液塞频率等参数。

图2 互相关法电极组安装示意图

Fig.2 Schematic diagram of cross-correlation electrode group installation

图3给出了换热测试段示意图。换热测试段包括紫铜管、PVC环空套管以及温度测量仪表。紫铜管长4 m、内径0.026 m、壁厚0.003 m，紫铜热导率为383 W·m-2·℃-1。环空套管由5节内径63 mm的PVC管构成，套管间采用法兰连接。实验选取4个截面作为温度测试截面。每个截面处紫铜管内布置两个热电偶探针，用于测量管内上下部流体的温度，两个热电偶间距为18 mm。环空内布置一个热电阻，用于测量冷却液的温度变化。在紫铜管外壁周向均布5个热电偶，用于测量紫铜管外壁周向温度。本文选取截面3、截面4之间的管段作为对流传热系数计算管段，此时热发展段长88>60，满足要求，温度系统的标定及动态响应详见文献[23,26]。

热流体定性温度TP取为

TP=(s3f1+s3f2+s4f1+s4f2)/4 (2)

式中，s3f1、s3f2、s4f1、s4f2分别为截面（s）3、4的上、下热电偶测量管内流体（f）温度，℃。液相折算Reynolds数SL、气相折算Reynolds数SG、液塞区Reynolds数S、液相折算速度SL、气相折算速度SG分别定义为

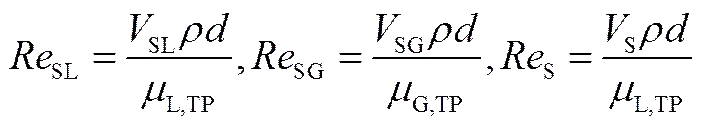
(4)

式中，S为实验测得的平均液塞速度，m·s-1；L,TP为某一气液速下，特征温度为热流体定性温度时的液相黏度，Pa·s；G,TP为某一气液速下，特征温度为热流体定性温度时的气相黏度，Pa·s；L为液相流量，m3·s-1；G为气相流量，m3·s-1；为管内截面积，m2。

以燕昌石化提供的LP-14白油与压缩空气作为实验介质，以加入10%乙二醇的水溶液作为冷却液，实验参数如表1所示，液塞区呈湍流状态。

表1 介质流速及Re范围

2 实验结果与讨论

图4为不同气相折算流速下液相折算流速对空气-油对流传热系数的影响。由图可以看出，不同气相折算流速下，随着液相折算流速的增加，TP逐渐增加且增速逐渐减小。这种变化的直接原因是随着液相折算流速的增大，液相增大，湍流程度增强，单位时间内流过的液体质量增大，系统总的换热量增大，增强流体与管壁之间的对流换热。间接原因是液速变化导致的段塞流流动特征的一系列变化使TP增加。液速的增大导致液塞区长度变大，液膜区长度变小[27]，液塞频率增大[22,28]，液塞区和液膜区的持液率略微增长[22]，因为液相的热导率远大于气相的热导率，所以液塞区越长，液膜区越短，液塞、液膜区持液率增大都会使流体与管壁的对流传热系数增大。液塞频率的变化也间接反映了液塞和长气泡交替出现带来的扰动。一方面频率越大，单位时间实验管道内通过的液塞数越多，液体流量越大，系统总的换热量增大，TP增加。另一方面，频率越大，液塞和长气泡交替出现的频率越高，气相对液相的扰动作用也就越强烈，对流换热得到强化。

图5为不同液相折算流速下气相折算流速对空气-油对流传热系数的影响。液速不变时，随气相折算流速的增大，TP略有增大。这是因为空气的比热容和热导率远远小于水的比热容和热导率，在液速不变的情况下气速的增大并不能使流体与冷却液之间的换热量显著地增大。一方面气速的增大使液相流体的掺混和边界层的扰动增强，增大对流传热系数；另一方面随着气速的增大，液塞区长度变小，液膜区变长，液塞频率变化不明显，液塞区、液膜区持液率略微下降。在二者的作用下，低气速时TP变化幅度较小，高气速时前者的增强作用大于后者，使TP增加。

图6为空气-水对流传热系数随液相折算流速的变化，与图5对比发现，相同气液速下，空气-水段塞流对流传热系数约为空气-油的10倍。由于油相Reynolds数较小，黏性力起主导作用，热边界层较厚；相反地，水相Reynolds数较大，惯性力影响更加显著，黏性力仅在靠近管壁附近的边界层内有较大影响，故水相内有更多流体微团参与湍流换热，从而导致空气-水对流传热系数远大于空气-油。

图7(a)、(b)分别为空气-油、空气-水对流传热系数强化比率随液相折算流速的变化，图中single为同一折算液速下实验测量的单相液体对流传热系数。比较表明空气-油对流强化比率远大于空气-水，说明气相加入造成的空气-油的对流换热强化作用显著大于空气-水。造成这种现象的原因可由Prandtl数解释。Prandtl数表征了流动边界层与热边界层的相对大小，假设管内纯液相流动时，油的Prandtl数远大于水的Prandtl数，油的热边界层比流动边界层厚，而油的流动边界层厚度远大于水的流动边界层。当气相加入后，油流动边界层获得更充分的扰动，从而导致换热强化，且气速越大，边界层扰动越剧烈，强化作用越大。

图8是气相折算流速SG为3.0 m·s-1，液相折算流速SL为1.0 m·s-1时，3种冷却液温度下第4截面管壁周向不同位置处对流传热系数的对比。从图中可以看出沿管壁一周，从管顶到管底对流传热系数不断增大，造成这种现象的原因是管顶位置由长气泡和液塞交替经过，而管底则始终覆盖一层液膜，气相与管壁的对流传热系数远小于液相，故管顶的换热强度低于管底的换热强度。而管壁中间位置处的对流传热系数测量值则比较接近平均实验对流传热系数，这是因为实验对流传热系数计算所采用的热流体温度是管内上下热电偶平均值，即管中心位置温度，与计算管壁中间位置处的对流传热系数所采用的热流体温度相接近。同一工况时，上壁面处的对流传热系数和下壁面处的对流传热系数值可相差2倍。

另外从图8中可以看出，冷却液温度不同，管截面周向不同位置处的对流传热系数也有较明显的区别。首先，在管顶及其附近位置处，冷却液9℃与冷却液17℃对流传热系数相近，冷却液4℃时对流传热系数则略小。在管底及其附近位置处，冷却液4℃与冷却液9℃对流传热系数相近，冷却液17℃时对流传热系数略大。这是由于管底始终覆盖一层液膜，冷却液温度越低，管底热流体黏度越大，导致热边界层越厚，换热越差。随着测温位置沿管壁逐渐升高，管壁从完全被液膜覆盖转换成长气泡和液塞交替经过，温差的作用越来越小。综上分析可以看出，管底部的热边界层厚度受温差影响巨大，从而导致对流传热系数随冷热流体温差呈负相关，热流体的黏度越大，温差的影响越大。

图9是折算气速SG为3.0 m·s-1时，冷却液4℃条件下管壁5个位置处（0°、-45°、-90°、-135°、-180°）实验对流传热系数随折算液速的变化。从图中可以看出，接近管底位置处两个热电偶测得的实验对流传热系数结果几乎完全相同，说明位置4与位置5处的对流传热系数受到的影响相同，接近管顶位置处两个热电偶测得的实验对流传热系数略有差别。这个微小差别的原因是，随着液相折算流速的增加，液塞头部气泡数量增加，卷吸的气泡在浮力的作用下聚集在管上部，且随着距液塞头部轴向距离的增大，不同径向位置处的局部含气率呈减小趋势[29]，位置2处有更多液相与管壁换热，故位置2处的对流传热系数略大于位置1处。另外，从上、中、下3个宏观位置来看，随着折算液速的增大，对流传热系数增速逐渐增大，这是因为液相折算流速的增大造成液塞频率增大、液塞占液塞单元的比率增大、气相加入对液膜扰动增强，这三者都造成了对流传热系数的增大。

综上所述，管顶与管底的对流传热系数的增速及主要影响因素是不同的，管底主要受气相强化冲击扰动边界层的作用，影响较大；管顶主要是液塞体的对流换热。计算平均对流传热系数时应对管顶与管底分别进行讨论。

3 冷却传热关联式与模型

图10为实验对流传热系数TP与Shah关联式[17]、Kago关联式[18]及Kim-Ghajar关联式[3,30]计算值的对比。当对流传热系数值比较小即液相Reynolds数较低时，关联式计算值略大于实验值，这是由于油相黏度较大，黏性力起主要作用，液速较低时，液膜区无扰动，相对平稳，液塞来临时对接近管壁处的液膜影响小，且冷却换热导致下壁面处的液膜一直处于冷却状态，使对流传热系数变化小于关联式预测值。液速在增大的过程中，Kago关联式对对流传热系数的估计过于保守，根本原因是其对液塞单元中的液相分数计算偏高。

表2为关联式计算值与对流传热系数实验值之间的最大偏差、最小偏差及计算值位于实验值10%范围内的数据量。Shah关联式及Kim-Ghajar关联式与实验值吻合良好，落入实验值10%范围内的计算值分别为82.5%、70%，Kago关联式由于计算的液相分数偏高，与实验值吻合度较低。

表2 实验值与关联式计算值误差

Shah关联式应用时需查图，Kim-Ghajar关联式参数因管路、物性变化而变化，这导致它们的程序化应用受到一定限制，Kago关联式[18]使用较方便，但针对加热工况下水平管段塞流换热提出。本文对其进行了修正，得到了适用于冷却条件下水平管段塞流换热关联式，分析表明82%的关联式计算值落入实验值-10%～10%内，拟合关联式如下

上述传热实验关联式依赖于具体的实验介质、装置等，研究具有普遍适用意义的冷却条件下段塞流传热模型具有重要价值。对管壁不同位置处的对流传热系数分析可以发现，气相加入造成的强化作用主要体现在管底位置处；管顶位置处对流传热系数的增速远小于管底的液膜区，本文认为气相加入造成的强化在这部分区域并不明显。根据局部对流换热的特点，本文对管内对流传热系数的组成做了如下假设(图11)。

图11 液塞单元分析

Fig.11 Analysis of slug unit

（1）两相段塞流对流传热系数由上部对流传热系数与下部对流传热系数依据与管壁的接触面积加权平均得到。

（2）下部对流传热系数为始终覆盖在管底的液膜f。

（3）上部总对流传热系数是依据液塞和长气泡占段塞单元长度百分比，将液塞体对流传热系数S和长气泡对流传热系数b加权平均得到。

（4）假设液塞内为纯液相，长气泡内为纯气相。

综上所述，两相段塞流对流传热系数为

G=·arccos(2/-1) (7)

=(Lf) (8)

其中，S为液塞体长度，m；b为长气泡长度，m；u为液塞单元长度，m；G为截面处长气泡与管壁接触的弧长，m；为液膜区液位高度，m；Lf为液膜区持液率。上述参数通过段塞流unit cell模型计算得到。S、b采用Gnielinski关联式[31]进行计算，以平均液塞速度作为液塞体内对流传热系数计算的特征速度。其余参数的取值及计算方式见文献[21]。实验观察到液膜区有气泡存在，且夹带气泡随气体折算速度增大而增多。液膜区对流传热系数f受气相加入扰动的作用，使热边界层与流动边界层发生变化从而产生强化传热，因此可通过建立混相与单相传热比值随气液折算速度比值及气液相Prandtl数的关系[式(9)]来得到。

其中，、、为待定参数，f为壁面位置5（-180°）处对流传热系数实验值，L为单相油对流传热系数实验值。

对所有冷却液温度下管底部的两相实验对流传热系数进行拟合（2=0.937），得到管底部液膜区对流传热系数f计算关联式

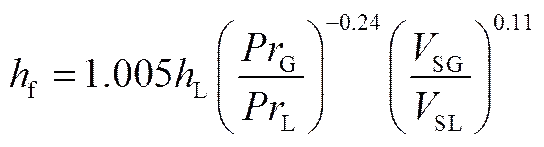
其中L为单相对流传热系数，由Gnielinski关联式[31]计算得到，式中速度取液相折算流速。

图12为冷却液4℃条件下本文建立的传热模型预测值与实验值的对比。从图中可以看出，多数模型计算值较好，分布在实验值±20%范围内，在对流传热系数较高时，模型预测值略高于实验值。这说明本文提出的气相强化因子主要作用于下部液膜区的理论可以正确地反映空气-油内的对流传热系数变化特征。

4 结 论

本文在水平实验管路上进行了无相变冷却条件下空气-油段塞流的换热特性研究，实验采用电容电极与热电偶、热电阻测量了段塞流流动与传热参数，分析了流动参数对传热参数的影响及空气-油传热特性与空气-水传热特性的区别。

研究发现，空气-油段塞流对流传热系数主要受液相折算速度的影响。外部冷却液温度越低，管底部热流体黏度越大，导致热边界层越厚，换热越差。受黏性力影响，空气-油段塞流对流传热系数远小于空气-水对流传热系数。受热流体热边界层厚度影响，气相加入造成的空气-油的对流换热强化作用远大于空气-水。沿管壁周向，从管顶到管底对流传热系数不断增大，管底的对流传热系数约为管顶的2倍。管顶与管底的对流传热系数的增速及主要影响因素是不同的，管底主要受气相强化冲击边界层的作用，管顶主要是液塞体的对流换热。

对Kago关联式修正，得到了适用于冷却条件下水平管油气段塞流的换热关联式，实验值与关联式预测值吻合良好。

本文根据沿管壁周向不同位置处对流传热系数受影响的因素不同，提出了以液膜区气液界面为分界面将液塞单元分为上下两部分，段塞流对流传热系数由上、下两部分的对流传热系数依据与管壁的接触面积加权平均得到的传热模型。模型计算值很好地分布在实验值±20%范围内，验证了模型的可靠性。

符 号 说 明

A——管内截面积，m2 d——内径，m HL——持液率 h——对流传热系数，W·m-2·K-1 L——长度，m DL——电容探针间的距离，m l——液膜区液位高度，m Pr——Prandtl数 Q——流量，m3·s-1 Re——Reynolds数 S——管壁接触的弧长，m T——温度，℃ Dt——信号延迟时间，s V——速度，m·s-1 m——黏度，Pa·s 下角标 b——长气泡 f——液膜 G——气体 G,TP——某特征温度下气体 L——液体 L,TP——某特征温度下液体 S——液塞 SG——气体的折算量 SL——液体的折算量 TP——两相 u——液塞单元

References

[1] SINGH P, VENKATESAN R, SCOTT FOGLER H,Formation and aging of incipient thin film wax-oil gels[J]. AIChE Journal, 2000, 46(5): 1059-1074.

[2] OLIVER D R, WRIGHT S J. Pressure drop and heat transfer in gas-liquid slug flow in horizontal tubes[J]. British Chemical Engineering, 1964, 9(9): 590-596.

[3] GHAJAR A J, TANG C C. Advances in void fraction, flow pattern maps and non-boiling heat transfer two-phase flow in pipes with various inclinations[J]. Advances in Multiphase Flow and Heat Transfer, 2009, 1: 1-52.

[4] GHAJAR A J, TANG C C. Heat transfer measurements for nonboiling two-phase flow//Handbook of Measurement in Science and Engineering[M]. New York: John Wiley&Sons Inc., 2013.

[5] GHAJAR A J, DOUGHERTY R L, KIM D,Multiphase heat transfer in flowlines and wellbores: final report-phaseⅠ[R]. Oklahoma: University of Tulsa Paraffin Deposition JIP, 1997.

[6] GHAJAR A J, DOUGHERTY R L, KIM D,Multiphase heat transfer in flowlines and wellbores: literature survey-partⅡ[R]. Oklahoma: University of Tulsa Paraffin Deposition JIP, 1997.

[7] RAVIPUDI S R. The effect of mass transfer on heat transfer rates for two-phase flow in a vertical pipe[D]. Nashville Vanderbilt University, 1976.

[8] ELAMVALUTHI G, SRINIVAS N S. Two-phase heat transfer in two component vertical flows[J]. International Journal of Multiphase Flow, 1984, 10(2): 237-242.

[9] KUDIRKA A A, GROSH R J, MCFADDEN P W. Heat transfer in two-phase flow of gas-liquid mixtures[J]. Industrial & Engineering Chemistry Fundamentals, 1965, 4(3): 339-344.

[10] GROOTHUIS H, HENDAL W P. Heat transfer in two-phase flow[J]. Chemical Engineering Science, 1959, 11(1): 212-220.

[11] KNOTT R F, ANDERSON R N, ACRIVOS A,An experimental study of heat transfer to nitrogen-oil mixtures[J]. Industrial & Engineering Chemistry, 1959, 51(11): 1369-1372.

[12] HANAOKA M. On upward flow of gas-liquid mixtures in vertical tubes(Ⅲ): Heat transfer results and analysis[J]. Bulletin of JSME, 1967, 10(42): 1008-1015.

[13] MARTIN B W, SIMS G E. Forced convection heat transfer to water with air injection in a rectangular duct[J]. International Journal of Heat and Mass Transfer, 1971, 14(8): 1115-1134.

[14] CHU Y C, JONES B G. Convective heat transfer coefficient studies in upward and downward, vertical, two-phase, non-boiling flows[J]. AIChE Symposium Series, 1980, 76: 79-90.

[15] VIJAY M M, AGGOUR M A, SIMS G E. A correlation of mean heat transfer coefficients for two-phase two-component flow in a vertical tube[C]//Proceedings of the 7th International Heat Transfer Conference. Munich, 1982, 5: 367-372.

[16] DUKLER A E, SHAHARABANY O. For Multiphase Processing, Studies in Intermittent (Slug) Flow in Horizontal Tubes: Design Manual Ⅰ-2[M]. New York: American Institute of Chemical Engineers, 1977.

[17] SHAH M M. Generalized prediction of heat transfer during two component gas-liquid flow in tubes and other channels[J]. AIChE Symp. Ser., 1981, 77: 140-151.

[18] KAGO T, SARUWATARI T, KASHIMA M,Heat transfer in horizontal plug and slug flow for gas-liquid and gas-slurry systems[J]. Journal of Chemical Engineering of Japan, 1986, 19(2): 125-131.

[19] MANABE R. A comprehensive mechanistic heat transfer model for two-phase flow with high-pressure flow pattern validation[D]. Tulsa: University of Tulsa, 2001.

[20] FRANCA F A, BANNWART A C, CAMARGO R M T,Mechanistic modeling of the convective heat transfer coefficient in gas-liquid intermittent flows[J]. Heat Transfer Engineering, 2008, 29(12): 984-998.

[21] NOVILLE I, BANNWART A C. Experimental study of the heat transfer in the intermittent horizontal two-phase flow pattern[C]//7th North American Conference on Multiphase Technology. Banff, 2010.

[22] 董传帅.气液两相段塞流无相变冷却过程流动与传热实验研究[D].青岛: 中国石油大学(华东), 2015. DONG C S. Investigation of flow and heat transfer characteristic of non-boiling air-liquid slug flow in cooling process[D]. Qingdao: China University of Petroleum, 2015.

[23] 王鑫, 董传帅, 张晓凌, 等. 空气-水段塞流冷却传热与相界面分布实验研究[J]. 中国科学院大学学报, 2017, 34(2): 232-236. WANG X, DONG C S, ZHANG X L,Investigation of heat transfer and interfacial distribution characteristic of air-water slug flow in cooling process[J]. Journal of University of Chinese Academy of Sciences, 2017, 34(2): 232-236, accepted.

[24] 王鑫, 祁雷, 何利民, 等.基于电容检测装置的油气两相流液塞运动速度和长度测量方法: 201410366839.7[P]. 2016-08-10.WANG X, QI L, HE L M,Capacitance detection device for measurement of liquid slug velocity and length in oil and gas two-phase flow: 201410366839.7[P]. 2016-08-10.

[25] 王鑫, 祁雷, 何利民, 等. 一种气液两相流相含率实时电容测量系统及其测量方法: 201410146048.3[P]. 2016-02-24. WANG X, QI L, HE L M,A gas-liquid two-phase flow phase holdup capacitance measurement system and real-time measurement method: 201410146048.3[P]. 2016-02-24.

[26] 王鑫, 徐静静, 祁雷, 等. 水平管空气-水段塞流冷却传热研究[J].工程热物理学报, 2014, (8): 1563-1568. WANG X, XU J J, QI L,Heat transfer in cooling process of air-water slug flow in horizontal pipe[J].Journal of Engineering Thermophysics, 2014, (8): 1563-1568.

[27] DESHPANDE S D, BISHOP A A, KARANDIKAR B M. Heat transfer to air-water plug slug flow in horizontal pipes[J]. Industrial & Engineering Chemistry Research, 1991, 30(9): 2172-2180.

[28] FARSETTI S, FARISÈ S, POESIO P. Experimental investigation of high viscosity oil-air intermittent flow[J]. Experimental Thermal and Fluid Science, 2014, 57: 285-292.

[29] WANG X, WANG T J, HE L M. Measurement of gas entrainment from stationary liquid slug in horizontal tube with double-sensor conductivity probe[J]. Flow Measurement and Instrumentation, 2012, 27: 81-91.

[30] KIM D, GHAJAR A J, DOUGHERTY R L. Robust heat-transfer correlations for turbulent gas-liquid flow in vertical pipes[J]. Journal of Thermophysics and Heat Transfer, 2000, 14(4): 574-578.

[31] GNIELINSKI V. New equations for heat and mass-transfer in turbulent pipe and channel flow[J]. International Chemical Engineering, 1976, 16(2): 359-368.

Heat transfer of oil-gas slug flow in horizontal pipe

WANG Xin, WANG Zhaoting, ZHANG Xiaoling, HE Limin

(College of Pipeline and Civil Engineering, Shandong Provincial Key laboratory of Oil & Gas Storage and Transportation Safety, China University of Petroleum, Qingdao 266580, Shandong, China)

The heat transfer in the cooling process of subsea oil and gas pipeline is a key factor of the flow assurance in offshore petroleum industry, such as wax, hydrate. In this study, capacitance probe, thermocouple and resistance thermometer were used to measure the flow and heat transfer characteristics of oil-gas slug flow in different cooling conditions and the effect of flow parameters on heat transfer of slug flow was analyzed. It was demonstrated that the convective heat transfer coefficient of oil-gas slug flow is mainly affected by the liquid superficial velocity. While the temperature of the outer cooling fluid is decreased, the viscosity of the inner thermal fluid at the bottom of the tube will increase and the thickness of the thermal boundary layer will be increased, therefore the heat transfer will be deteriorated. Also the convective heat transfer coefficient of oil-gas is much lower than that of water-gas due to the different viscous force and boundary layer. The local convective heat transfer coefficient is increasing from the top to the bottom of the tube along the circumferential direction. Moreover, the correlation and heat transfer model of oil-gas slug flow under cooling condition were presented.

gas-liquid flow; heat transfer; multiphase flow; cooling condition; slug flow

10.11949/j.issn.0438-1157.20161556

O 359

A

0438—1157（2017）06—2306—09

王鑫（1973—），男，博士研究生，副教授。

国家自然科学基金项目（51376197）。

2016-11-03收到初稿，2017-03-03收到修改稿。

2016-11-03.

WANG Xin, wangxin@upc.edu.cn

supported by the National Natural Science Foundation of China (51376197).