公共租赁住房再分配机制的优化
——基于公平与效率的视角
2017-06-05邓红平
邓红平 卢 丽
(华中师范大学 经济与工商管理学院、湖北房地产发展研究中心, 湖北 武汉 430079)
公共租赁住房再分配机制的优化
——基于公平与效率的视角
邓红平 卢 丽
(华中师范大学 经济与工商管理学院、湖北房地产发展研究中心, 湖北 武汉 430079)
构建合理有序的公共租赁住房再分配机制是其可持续运转的关键,一般采用交换与调整两种方式。现行公共租赁住房交换机制是一种帕累托改进的机制,但若能增加原租户偏好表达个数及两两交换的次数,运用G-TTC机制自动匹配,理论上可得到帕累托最优的分配结果。公共租赁住房调整机制的关键问题在于如何平衡原租户与新租户间的公平与效率,简单地将原租户与新租户分开配租的现行调整机制存在公平与效率的提升空间。本文引入三种改进的调整机制,得出TTC及其等价的YRMH-IGYT机制可能满足帕累托最优、个人理性和无策略的性能;而SD机制则可能是更为公平的调整机制。
公共租赁住房再分配机制; 交换; 调整 ; 优化
一、引言
公共租赁住房(简称公租房)分配可分为初分配和再分配两阶段,主要研究框架如图1所示。我国大部分城市已经历公租房的初分配,部分公租房租户由于家庭、工作等原因,产生了调换(交换和调整)公租房的需求;这些需求与符合条件的新一轮申请者的配租需求,共同构成了公共租赁住房再分配问题。对于价格机制不能充分发挥作用的公共租赁住房再分配市场,如何构建合理有序的再分配机制是其可持续运转的关键。

图1 公共租赁住房分配的分类和对象
公租房再分配机制的关键问题在于如何考虑有调换需求的原公租房租户(简称原租户)与符合准入条件的新轮候人(简称新租户)的公平与效率问题。理论上合理且现实中常用的一般有两种方式:(1)交换,是指原租户在原租住的住房(简称已租房)范围内进行的交换;(2)调整,是指原租户放弃已租房,将其与空房源①一起纳入待分配的房源中,并与新租户一起参与空房源的分配。我国公共租赁住房再分配交换机制只有北京、深圳等少数城市出台了公租房交换办法,其基本思路是由政府搭建信息平台,让群众自找对象、实现无偿自愿调换,以有限次数的两两交换居多。这种交换机制是一种帕累托改进的机制,却不一定能得到帕累托最优的结果。再分配的调整机制则有北京、重庆等地提出可让原租户放弃已租房,在空房中再次进行选择。公租房的调整机制不仅涉及原租户的利益,也涉及新租户的利益,简单将新旧租户隔离分配的现行机制使双方感受到歧视,故如何体现混合排序的公平性以及平衡新旧租户的租房效用,使调整成为一类更为复杂的再分配问题,制定相应政策时应持谨慎原则。从现有的调整机制看总体上是控制原租户参与空房分配的②。
本文将延续公租房再分配交换与调整的话题,为公租房的合理调换提供一种新的政策研究思路。首先,分析现行公租房交换机制的优点与不足,以原租户的效用为逻辑起点,引入Gale的顶层交易循环机制改进原租户的再分配交换效用。其次,分析当前公租房调整机制的复杂局面,以原租户不降低效用和无嫉妒式公平为逻辑起点,引入三种改进的调整机制,力图优化公租房资源配置的结果。
二、文献回顾
公共租赁住房再分配机制的优化理论与实验研究国内尚不多见。而国外从稳定配置理论到公共住房分配的市场设计研究很是值得我们借鉴③。
1.再分配匹配理论
公租房再分配理论可分为交换与调整两类。
(1)交换。住房已被原租户全部占用情况下的交换匹配机制研究。与国外文献中的“住房市场”(house market)相对应。Shapley和Scarf首次将匹配理论运用到住房这类不可分割物品的研究中,建立了住房分配博弈模型,并证明在任何市场中不管有没有竞争价格(市场出清价格)都存在核,他们引入Gale的顶层交易循环算法(Gale’s top trading cycles,G-TTC)求解核之唯一帕累托最优匹配结果④。Roth和Postlewaite因“住房市场”中只需占有住房的原租户对住房表达严格的偏好,即可交换住房,而将之定义为单边匹配市场⑤。Ma证明了G-TTC交换的结果不仅是帕累有效的,还是个人理性及偏好表达无策略性的⑥。Sönmez和Ünver将G-TTC机制称为关键机制⑦,其他许多研究中设计的优化机制都是以它为原型的改进,或将现实中应用的机制与之进行比较。
(2)调整。参与人包含原租户与新租户,可供分配的房源含已租房与空房源,且一套住房至多只能分配给一名申请者情况下的匹配机制研究。与国外文献中的“存在部分租户”(house allocation with existing tenants)相对应。通常,调整是有优先权与租户偏好的双边匹配市场,由于需要权衡原租户与新租户的公平和效率问题,使得这类分配变得更为复杂。如果期望得到至少是帕累托改进的分配结果,那么原租户的住房福利应不下降,Abdulkadirogˇlu 和Sönmez的理论研究表明,随机序列独裁(random serial dictatorship with squatting rights ,RSD)机制因不能保证原租户的住房效用至少等于其已租房,在“存在部分租户”的市场中并不是帕累托有效的匹配机制,他们改进了Gale的TTC机制(简称TTC机制),在假设行为人完全理性的条件下,运用数理分析方法证明了该机制分配结果的效率优于RSD机制;同时他们设计直观易懂的TTC机制等价算法“你要我的房子,我要你的排序号”(You request my house—I get your turn ,YRMH-IGYT)来求解该问题的帕累托最优结果;并证明TTC机制是可以达到帕累托最优、个人理性及无策略性标准的⑧。随后,Sönmez和Ünver在2005年分析了RSD的两种改进调整机制,即“基于核的”机制和1999年提出的改进的TTC机制;基于核的竞争机制首先设定原租户的初始禀赋为已租房,新租户的初始禀赋则随机分配一个空房,然后运行G-TTC机制得到住房市场的核,并决定最终的分配结果。他们指出了“基于核的”机制是TTC机制的特例,但其偏向于新租户特点受到批评⑨。在2010年,Sönmez和 Ünver基于三个弱中性和连续性的公理,分析了TTC的等价机制——YRMH-IGYT机制的全部特点,证明了YRMH-IGYT机制是帕累托有效性、个人理性、无策略、弱中性和连续性的⑩。
2.再分配匹配的实验
再分配匹配的实验研究多以存在部分租户的住房匹配(调整)为实验研究对象。Chen and Sönmez最早利用实验来检验再分配匹配机制的性能,通过开展实验室实验比较了美国大学宿舍分配常用的RSD机制与TTC机制(YRMH-IGYT)的性能。他们希望通过实验室实验来检验和证实:当有限理性个体加入不完全信息匹配市场时,TTC机制与RSD机制在匹配中的真实效果。他们的实验结果显示,不同机制的效率以及已有宿舍的学生申请再分配的参与率表现不同,TTC机制下的效率及参与比例都显著高于RSD机制,但是参与者真实偏好的揭示二者没有显著差异,不过,他们并未分析被试扭曲偏好的原因。在2002年的实验基础之上,Chen and Sönmez设置了完全信息的实验环境,设计了允许申请人决定是否参与再分配的“有选择的顶层交易循环机制”(top trading cycles with option,TTC-opt),与TTC及RSD机制进行比较,实验结果显示TTC机制和TTC-opt机制在效率方面显著优于RSD机制,它们均可以达到帕累托最优,故可以TTC机制取代RSD机制进行大学宿舍分配。之后,Guillen和 Kesten针对同样的问题提出了一种变种的GS匹配机制,从理论上证明这种机制等同于麻省理工学院的宿舍分配机制(MIT机制);并通过实验模拟大学生宿舍分配,比较MIT(变种G-S机制)与TTC机制的表现,结论表明,在效率以及原租户的参与率上G-S机制都优于TTC机制,但对于参与者真实偏好的揭示,二者没有显著差异。
在国内,邓红平、罗俊首次在实验室模拟了我国公租房匹配情景,考察G-S与IIRSD的性能,设计了嫉妒指数来评判两种机制的公平性,并得出G-S机制在公平与效率上都优于IIRSD的结论,但被试的真实偏好扭曲程度依然较高,其原因主要在于参与人的有限理性与风险回避态度。
三、前提假设与检验指标
在对公共租赁住房再分配机制的优化路径展开讨论之前,我们对本文理论研究所用的概念用数学语言进行了描述;并对研究前提、评价指标等进行了限定性的假设和界定。
在公共租赁住房再分配中,参与分配的申请者分为已占有房屋的原租户和符合条件的新租户,房源分为原租户占有的已租房和待分配的空房源,为下文讨论方便,我们定义全部租户的有限集合R={R1,R2...,Rn}=R′∪R″,其中原租户集合为R′={R1,R2...,Rm};符合配租条件的新租户集合为R″={Rm+1,Rm+2...,Rn}。定义全部公租房房源的有限集合为H={H1,H2...,Hn}=H′∪H″,其中原租户占用的已租房集合为H′={H1,H2...,Hm},待分配的空房源集合为H″={Hm+1,Hm+2...,Hn},定义调整机制下划拨给原租户的空房源集合为H‴∈H″={Hm+1,Hm+2...,Hk},k≤n;轮候人对公租房房型的严格偏好集为P(R)。对H中的任意房型Hi和Hj,若有HiP(Rk)Hj表示租户Rk偏爱房源Hi甚于Hj。房源Hq对租户Rk的价值为集合U={Ukq},其中Ukq≥0。也即是说当Rk匹配到房型Hq时的效用为Ukq>0 ,而未匹配到房型Hq时的效用则为Ukq=0。可以序数形式表示。
(1)假设所有原租户与新租户都是已通过审核,具备配租资格。
(2)假设每个申请者只可分得一个房源,且对所有房源有严格的偏好,可以序数形式表示。
(3)假设有必要时,管理部门为申请者安排优先序并公示,可以序数形式表示。
匹配结果需要科学的判断与评价,当价格机制不能发挥作用时,一个科学的匹配机制应该能“诱导”参与人诚实地表达真实偏好,并在这样的偏好下公平有效地配置资源。故而虽然我们追求的目标为公平与效率的优化,然而个人理性与偏好表达真实度(无策略性)也是机制设计的重要考察指标。
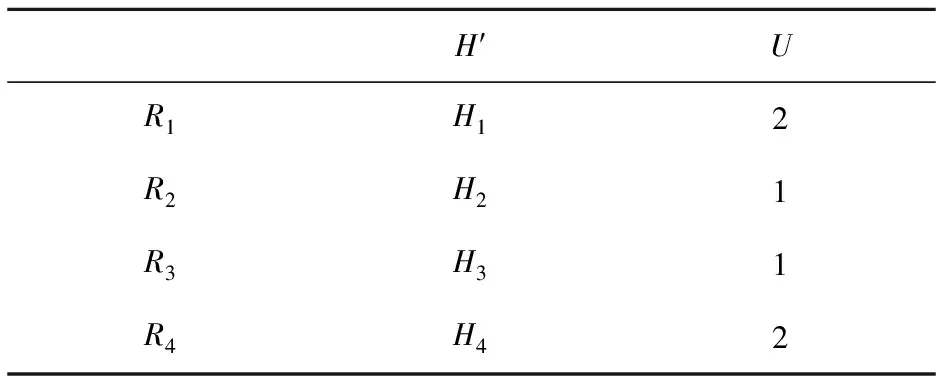
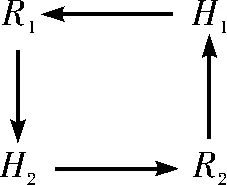
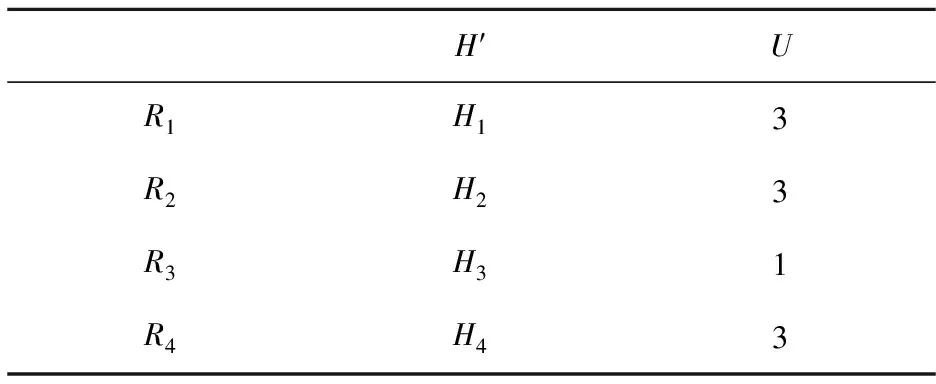
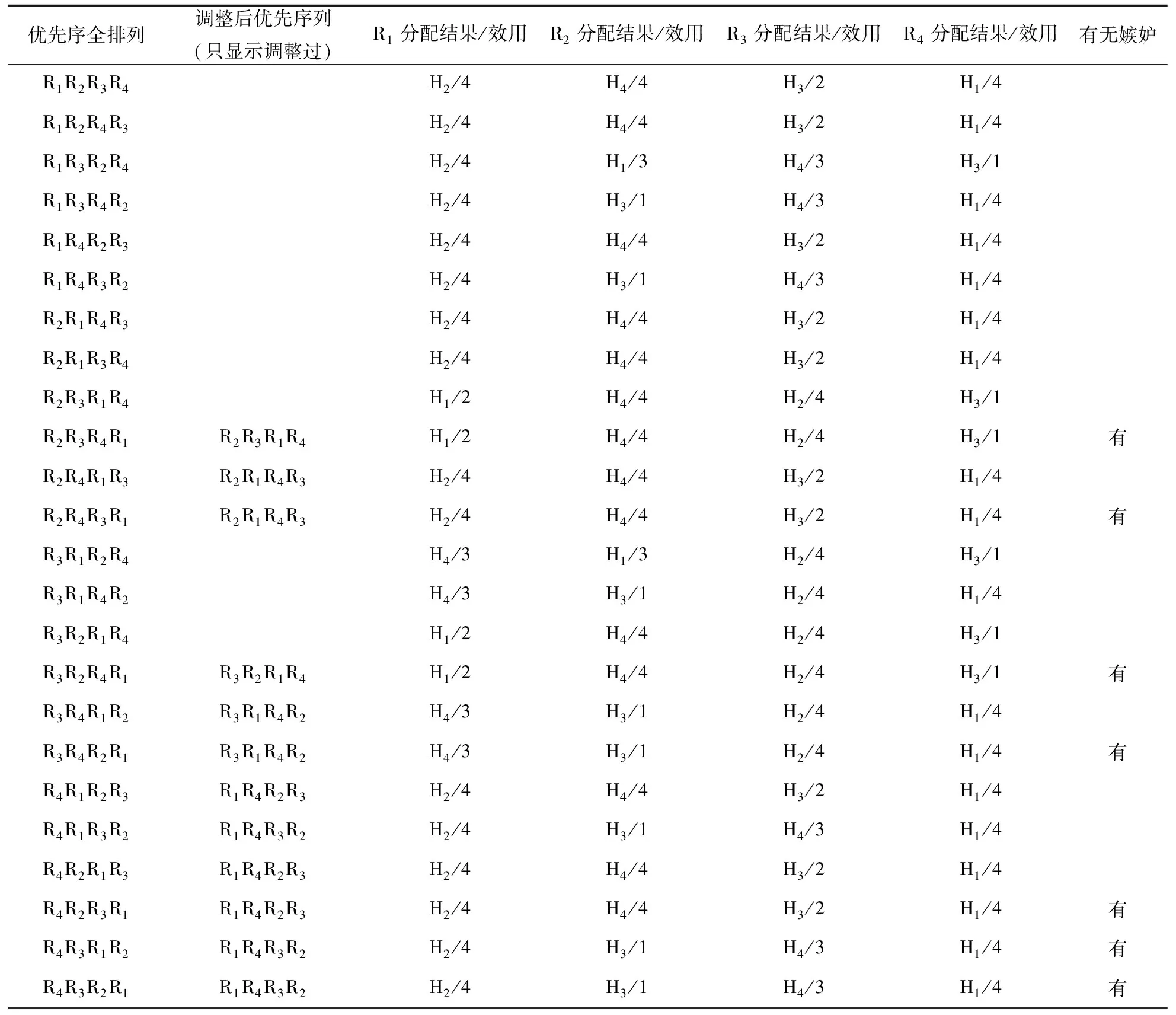
(1)帕累托最优。帕累托最优是公认理想的效率状态。对某种匹配机制M,其租户集合R的效用集为U,当有另一个匹配机制M′使得U′>U时,∃Rk∈R,在M及M′下的分房效用分别为Ukq及Ukq′且Ukq′ (2)公平。公租房的保障性质决定了其分配以公平为价值取向。免于嫉妒是公平的衡量标准之一,是指在一个社会分配中,每一个参与者都更偏好他自身的状况,没有人更偏好其他人的选择,整体都不存在嫉妒他人的情况,每个人都不想改变自己的分配结果,则称这个分配是公平的。在以优先权与偏好表达为基础的双边匹配市场中,我们在优先序、偏好表达及分房效用以数值表示的基础上,以嫉妒指数来定量考察机制M基于优先权的无嫉妒式公平问题。假设优先序为i,j(i (3)个人理性。一个再分配机制M是个人理性的是指,∀Ri∈R′,对其新配租的房子Hk和已租房Hi,总有HkP(Ri)Hi;∀Ri∈R″,其新配租的房子为Hk,总有HkP(Ri)H0。也就是说,对于任意的原租户,再分配的房屋优于或等于原租户的已租房,确保他们参与交换或调整是没有风险的;对于任意的新租户,匹配到住房的状态一定好于没有匹配到住房的状态。 (4)无策略性。一个再分配机制M的无策略性是指,∀Ri∈R,Ri表达真实偏好和策略偏好下分配到的公租房分别为Hp和Hp′,若总有U(Hp)≥U(Hp′),说明机制M下,任意租户表达真实偏好得到的住房效用总是优于或等于表达策略偏好下得到的效用,亦即当任何申请者都无法从扭曲偏好的决策中获益时,表达真实偏好是一个占优策略。 (一)现行公租房交换机制分析 公租房再分配中的交换主要为提出房屋交换申请的原租户提供交换信息平台,满足他们的交换需求,增强其住房效用,提升公租房使用的社会福利。然而在我国的公租房再分配制度建设中,专门推出公租房交换解决方案的城市并不多见,我们对国内几大城市根据实际情况自行设计的再分配交换机制进行了梳理,统计结果如表1所示。 表1 部分地区公租房交换统计表 从各地交换办法来看,北京、深圳、杭州、南昌都对原租户因工作、家庭生活等原因需交换已租房的情况,推出了公租房交换管理办法。较为统一的是,以上城市均建立了信息化的交换平台,深圳、杭州、南昌的交换原租户可通过登录交换平台填写详细已租房信息和交换目标住房信息,审核通过后,根据平台发布的相关信息即可寻找合适房源在市区内进行自行配对。北京市则是原租户首先在保障房管理部门进行登记,审核通过后,由工作人员统一录入到官网平台,然后有交换需求的原租户通过平台查询合适房源,自行配对,两两交换,达成一致意见后,双方需统一到住房保障管理部门签订相关协议,完成交换。另外,杭州市还给出了具体的操作流程图为参与交换的原租户提供便利;深圳在交换管理办法中尝试制定了相关法律条款制约交换原租户的违约行为。总体来看,上述城市的公共租赁住房交换流程,除部分顺序稍有变动外基本相似,一般流程如图2所示。 图2 现有公共租赁住房交换一般流程 通过表1的归纳我们还可以看到,对原租户可交换的房源,75%的城市限定为与原租户同户型(居室数相同)的房源,50%的城市只能交换一次,以解决因房源楼层、区位不能满足工作、生活需求的问题。此外,各地原租户交换房屋能获取较为完全的供求信息,且只需原租户表达偏好并无交换的优先序,属于典型的完全信息单边匹配市场。整体来看,虽然自愿交换但也用诸多限制来维护公开、透明的操作流程以及结果无异议。 结合表1和图2可以看出,现有公租房交换机制秉着信息公开,自愿交换的基本方针,并不对有交换需求的原租户进行排序,也即不必考虑基于优先序的公平问题,而只关注原租户的交换利益。原租户间的两两交换是建立在已租房基础上的一种帕累托改进,但却不一定是帕累托最优的,其原因在于三个方面。 第一,有限理性的租户在复杂环境中的认知能力有限。各地由政府搭建平台、群众自找对象、无偿自愿交换的方式构造了一个良好的信息环境,并充分尊重租户的交换意向及能动性。这一流程,较好地解决了参与交换的原租户间信息不对称的问题,理论上为参与交换的原租户节约了寻找合适房源的成本。但在实际操作中,对于有限理性的交换原租户来说,当遭遇复杂的交换环境时(如同时3人以上交换才能满足需求),寻找合适的交换租户需要耗费相当的精力和成本,当交换循环圈超出其认知能力时交换成功率将降低,参与交换的原租户可能因未能发现合适房源选择放弃,导致可供交换的房源“基数”减少,房屋交换的成功率进一步降低。 第二,限制参与交换的原租户的偏好表达。如各地均对发布意向交换要求的房源个数、两两交换的次数进行限制,并要求每次交换需有审核方能实施。在价格机制不能充分发挥作用的市场,对于偏好表达的限制应该谨慎。如果放松某些限制,使得租户充分表达自己的真实偏好,运用信息系统自动依据这些偏好寻找出更大的循环交换圈后集中交换,则租户的个人效用和公租房分配的整体福利可能进一步提高,直至达到帕累托最优的目标。 第三,机制的选择。能够让原租户表达偏好后找出所有匹配交换循环圈,以多重两两交换的方式得到帕累托最优分配的是G-TTC机制。 (二)公租房交换机制的优化 我国公共租赁住房再分配的交换机制是较为典型的完全信息单边匹配问题。国外对此问题的研究起步较早,在理论上有重大的突破并经过不少实验的检验与市场设计的成功验证。其中最著名的G-TTC机制运行过程如下: (1)原租户表达对所有可交换房源的偏好顺序。 (2)建立一个顶层交换通道。 (3)将所有原租户表达的第一偏好的房子置于顶层交换通道中,如果顶层交换通道中有n位轮候人的偏好形成了一个闭合循环圈,则让该n位原租户的房子互换,交换过的人与房均退出分配。 (4)在余下还没有交换到房子的原租户中,如第一偏好的房已被选走,则将其第二偏好的房置于顶层交换通道中,同样,在这些余下的轮候人中若某n位轮候人的偏好能形成一个闭合循环圈,则让该n位轮候人的房子互换并退出分配。 (5)重复前一个步骤,直到所有人都交换完毕退出,分配过程结束。 为清晰原理,我们举例如下: 假设存在4位需要交换房屋的原租户R′={R1,R2,R3,R4},他们的已租房集合为H′={H1,H2,H3,H4}。已租房效用为U={U11,U22,U33,U44},此时有4≥Ukq≥1,意即如Rk匹配到的Hq为自己第一、第二、第三、第四喜欢的房源的令牌效用分别为4,3,2,1。 情况1:4位原租户的已租房效用及交换的偏好表达如表2-1和表2-2所示。 表2-1 已租房及效用 表2-2 交换偏好表达 如果机制限制交换意向表达个数为1个,此时原租户只能表达P(R)=1时的偏好。4名原租户能看到的信息中,可实现图3-1的循环圈,而不能实现图3-2的循环圈,其交换结果如表2-3。G-TTC机制下允许原租户表达对4个房源的偏好,则结果实现两对互换,交换结果及效用如表2-4。 图3-1 R1-R2间交换循环圈 图3-2 R3-R4间交换循环圈 H′UR1H24R2H14R3H31R4H42 表2-4 G-TTC机制下交换结果及效用 情况2:4位原租户的已租房效用及交换的偏好表达如表3-1和表3-2所示。 此时根据第一偏好就有图4所示循环圈。要实现表3-3所示最优结果有两种途径,一是需要三个两两交换R1-R3,R3-R2,R2-R4,但如果机制限制每人只能两两交换一次,因R3、R2要交换两次而不能实现帕累托最优的交换结果;或者4人同时理解了分配结果并约定各类手续及搬迁事宜,交换的租户需有相当的认知与处理问题的能力。 表3-1 已租房及效用 表3-2 交换的偏好表达 表3-3 G-TTC机制交换结果及效用 图4 R1-R2-R3-R4间交换循环圈 通过以上分析,可得出如下命题。 命题1:在公租房交换机制中,对于给定的原租户可表达的交换意向个数p,p 命题2:在公租房交换机制中,给定的允许两两交换次数p,p 在自主寻找信息、自愿匹配、两两交换的机制下,即使允许表达多个甚至所有m个房源偏好,且允许有m-1次交换,原租户面对情况2或者更为复杂的交换情况,虽然也可以通过多次交换达到和G-TTC一样的结果,但是需要原租户耗费大量的时间和精力,且需拥有强大的计算能力与协调能力才能完成多次交换的任务。 G-TTC机制能激励原租户表达真实偏好,原租户不需要担心在循环中丢失对已租房的租用权,表达真实的偏好是占优策略;相比我国的两两交换、自行配对的现行机制来说,如能在计算机信息系统中,允许原租户提交对房子的全部偏好序,运用G-TTC机制进行大范围的循环计算,可更加快速和简便地形成匹配交换循环圈,得到帕累托最优的匹配结果,提高原租户的公租房使用效率及社会整体分配福利,使资源得到更合理有效的利用。同时省去了原租户寻找合适房源的过程,为原租户节省了相应的时间和交易成本,也提高保障房管理部门房屋交换的执行效率。 以上理论分析可看出G-TTC机制分配效率优化的可及性。然而,得到帕累托最优结果的前提:一是真实偏好表达;二是需表达对所有房源的偏好。理论上,G-TTC机制是能满足无策略的机制,但从相关实验来看,在有限理性与风险偏好等因素的作用下,参与人表达真实偏好的情况也并不令人满意,尽管在G-TTC机制下改变偏好并不能改善福利。至于公租房交换房源的数量,可由住房保障部门控制在合理的范围内,房源太少或太多(积累成百上千的交换需求后再启动交换程序)都不可取,设置时间节点,或者房源积累到一定数量后,再开放交换程序是可尝试的方法。 此外,G-TTC机制下形成的交换循环圈链条长度越长,实践中后续搬迁越难以实施。首先,如果通过多次两两交换能达到帕累托最优的结果,实践中意味着有的租户需要多次搬迁,甚至在某次交换中遭遇临时效用下降的情形,导致租户不愿实施交换;其次,如果在长链条下让申请者约定在同一时间内进行搬迁,在实际操作中则可能会出现协商不一致、时间不易统一等状况,导致在具体操作过程中G-TTC机制循环圈虽然形成,却无法及时完成交换的情形。当然较之肾脏匹配,公租房的特殊性减缓,公租房的装修设计以及配套设施强调入住方便,降低了搬迁的阻力;G-TTC机制下的交换通常提升了申请人的住房的效用,如无特殊原因,原租户愿意集中搬迁。如由公租房管理部门统一受理交换相关事宜,则可进一步提高再分配交换的执行效率和社会福利。 (一)现行公租房调整机制分析 公租房再分配中的调整是指租户中既包含原租户又包含新租户,待分配的房源亦包括已租房和空房源的房屋再分配问题。调整是介于初分配与再分配交换之间的一种更为复杂的分配问题,其关键在于原租户与新租户间公平与效率的权衡。原租户绝对优先或者新租户绝对优先,或者将新老租户完全隔离分配均不是管理部门和租户满意的安排。那么混合配租不可避免,从社会福利的视角看,至少保证原租户的福利不下降的调整是合理的,如果某种机制使得某原租户再分配效用下降,这种分配结果显然不是帕累托最优的,甚至不能称为一个帕累托改进;而从公平的视角看,如果混合配租时,存在合理的优先序,则应考虑该种优先序下的公平问题。 为考察我国公租房现行的调整机制,我们对为数不多的几大城市的调整方案进行了梳理,统计结果如表4所示。 表4 部分地区公租房调整统计表 注:调整机制:A:随机匹配,即轮候人与房源随机配对;B:序列独裁(serial dictatorships,SD),即按选房优先顺序依次选房,第一名首先选择,第二名在余下的房源中选择,以此类推。 杭州、重庆较早提出公共租赁住房房源调整通知,2014年12月北京市也针对原租户因结婚、生育等原因致使人口增加产生的住房调整需求,公布了详细具体的公租房调整范围、原则及流程方案。从表1可以看出,杭州、重庆都规定了可调整的房源为同小区符合调整需求的空房源,杭州市额外给出若同小区(项目)内确无相应户型房源的,住房保障部门可酌情提供就近房源的方案。北京市在房源调整的来源区位上未做具体规定,只将通过审核的原租户按调整审批意见时间先后,在调整轮候需求库中进行排序,等待需求项目中合适房源套型出现,然后配租;此外还可登记参加市级或区县其他公租房项目摇号配租活动。总体来看,上述城市的公共租赁住房调整流程,均重新给予原租户优先序及偏好表达权,然后运用匹配机制进行匹配,一般流程如图5。 图5 现有公共租赁住房调整一般流程图 通过表4和图5的归纳可见,各地方案都考虑了原租户因人口、租金、搬迁等原因引发的调整需求,尽管细节有所不同,但均对原租户重新排序轮候并给予偏好表达的机会。优先序须公示而偏好为私人信息,使得调整成为一类不完全信息的双边匹配市场。从现有的调整机制看,管理部门也力求在原租户与新租户的公平与效率间保持平衡。一般采用专门为原租户提供房源的实施办法,部分保护了原租户的利益,但原租户与新租户均不一定能达到公平或效率最优的目标,其原因在于三个方面。 第一,偏好表达的限制。上述城市对于申请调整的原租户,在审核通过后统一进入轮候库,根据规定流程按需求划分部分空房源进行配租,这种方法简单易行,考虑了原租户需求同时,减少了不必要流程和配租环节。但从整体看,新租户不能表达对划拨房源的偏好,原租户也不能表达对其他空房源的偏好,偏好表达不完全,即使都为真实偏好,调整结果也难以达到帕累托最优。 第二,优先权安排失衡。在划出的专门房源中让原租户优先于新租户,而在其他房源中则新租户优先,表面上看,分别保护了原租户与新租户的利益,尽管原租户与新租户的效用可能均有提高,但将新旧租户隔离安排优先权与匹配有失公允,如能混合安排新旧租户的优先序,公平或效用可能存在进一步改进的空间。 第三,匹配机制的选择。与交换机制不同,现行调整机制大多采用在分割的房源中,按某种优先序依次选房的匹配机制,对原租户来说,如能保证先选后腾退,则是一种帕累托改进的分配,却不一定是公平或有效的分配。 为说明以上三个问题,我们举例如下。 假设存在4位参与调整的租户有限集合为R={R1,R2...,R4}=R′∪R″,房源集合为H={H0,H1...,H4}=H′∪H″。其中需调整的原租户集合为R′={R1},他们对应的已租房集合为H′={H1};新租户集合为R″={R2,R3,R4},待分配的空置房源集合为H″={H2,H3,H4},其中划拨空房源H4满足原租户R1的调整需求,此时,给新租户的房源变为H″={H2,H3,H1},H0表示未分到房。租户的租房效用集合为U={Ukq},k,q=1,2,3,4此时有Ukq=0,1,2,3,4,意即如Rk匹配到的房源Hq为自己第一、二、三、四喜欢的房源的效用分别为4,3,2,1,未分到房的效用为0。假定3位新租户的优先序为R2,R3,R4,租户的初始状态及交换的偏好表达序列P(Ri)如表5-1和表5-2,则分配结果如表5-3所示。 表5-1 调整前的状态 表5-2 申请者的房源偏好表达 表5-3 调整后的结果 表5-3的分配结果可以看出,调整之后,每个租户的租房效用都得到改进,但是原租户R1与新租户R2并未分到自己最中意的房,如果允许交换,他们互换可以进一步改进效用到4,可见这样的分配并非帕累托最优的,即使允许租户在分配以后交换来达到最优效果,比一次完成执行效率低。从公平的视角看,因为优先序的隔离安排,原租户R1与新租户R2可能相互嫉妒。 命题3:对于新旧租户分离排序匹配的现行调整机制M,∃Ri∈R′,∃Rj∈R″,对于∀Hi∈H‴,∃Hj∈H-H‴-Hi,HjP(Ri)Hi,HiP(Rj)Hj,则机制M是非帕累托最优且非公平的机制,却是个人理性且无策略的机制。 以上分析可见,现行的调整机制存在改进的空间。 (二)公租房调整机制的优化 在不完全信息双边匹配市场中,简单地将原租户与新租户完全隔离排序并分配使得新旧租户都难以满足公平或福利最大化的目标。在各地不断的尝试创新中,北京市提出在调整房源不充足的前提下,原租户可申请参加其他市级或区县的公租房摇号配租活动,首次将新旧租户纳入统一分配框架,是更具普适性的调整机制。本文引入三种国外存在部分原租户住房分配相关理论,期望探明我国公共租赁住房调整的优化方向。 1.保留权利序列独裁机制 保留权利序列独裁(serial dictatorship with squatting rights ,SD)机制的流程如下: (1)在信息不完全的调整市场中,原租户可以选择参与新的配租活动或保留其已租房不参与再次配租。选择参与重新配租的原租户其已租房将同待配租房源一起作为空房源进入分配程序。 (2)管理部门按照统一的规则(随机、综合评分等)决定所有参与者的优先序列并公示。 (3)优先序排第一的申请者可选择房源中其最偏好的住房;优先序排在第二位的申请者可选择剩余房源中他最偏好的住房;以此类推,直至房源分完或无人参与。 SD尤其RSD机制是国内外广为应用的匹配机制,保障了某种优先序列下的无嫉妒式公平,但从效用的角度看,仍存在改进空间。 假设存在4位参与调整的租户有限集合为R={R1,R2,R3,R4}=R′∪R″,房源集合为H={H0,H1...,H4}=H′∪H″。其中需调整的原租户集合为R′={R1},他对应的已租房集合为H′={H1};新租户集合为R″={R2,R3,R4},待分配的空房源集合为H″={H2,H3,H4},H0表示未分到房。租户的房源效用集合为U={Ukq},k,q=1,2,3,4,此时有Ukq=0,1,2,3,4,意即如Rk匹配到的Hq为自己第一、二、三、四喜欢的房源的效用分别为4,3,2,1,未分到房的效用为0。假定4位租户的初始状态及交换的偏好表达序列P(Ri)如表6-1和表6-2。 表6-1 调整前状态及效用 表6-2申请者的房源偏好表达 在不完全信息环境下,原租户R1并不了解其他人的偏好信息,此时他有两种选择:一是继续租用H1,不参与此次调整配租程序;二是放弃H1和新租户一起参与重新配租来达到住房调整的目的。 如果R1选择参与调整,由表6-2中的偏好序P(R)以及24种优先序全排列,可计算出表6-3的匹配统计结果。 从表6-3可以统计出,在新旧租户共同排序时,有66.67%的概率原租户的租房效用高于已租房,其中分到最喜欢的房子H2的概率为50%,8.33%的概率与已租房相同,但也有25%的概率,原租户R1可能分到房源H3,住房效用下降。从而导致整体再分配不能满足帕累托有效的目标。此时,害怕风险的原租户也许因为不确定的结果而放弃调整,虽然可以保证自己现有的利益,但却失去75%改进效用的调整机会。 表6-3 SD机制下分配结果 命题4:对于保留权利的序列独裁调整机制M,有优先序为i原租户Ri∈R′,其已租房为Hi∈H′,调整后的公租房为Hk;若存在更高优先序j的租户Rj∈R,若对∀Hj∈H-Hi,有HiP(Rj)Hj,则将Hi分配给Rj,若有Uii>Uik,则机制M是非帕累托最优且非个人理性的机制,但却是公平和无策略的机制。 尽管保留权利序列独裁机制为原租户在区位和房源上提供了更大的调整空间,但实际操作中优先序的确定以及各类租户的偏好都将影响最终的分配结果,使得调整不能保证原租户再分配的住房效用大于或等于原租房,厌恶风险的原租户即使有调整需求,但可能会选择保留自己当前住房而放弃参与再分配,导致调整机制的实践意义降低。尽管SD机制在混合排序下能满足无嫉妒式公平,但理论界与实践界均不懈努力寻求更接近帕累托最优的调整机制。 2.顶层交易循环机制 存在原租户情境下的,由G-TTC机制改进而来的顶层交易循环机制(TTC),便是一个追求效率完美的再分配调整机制。其运行流程如下: (1)管理部门按照统一的规则(如随机、综合评分等)决定所有参与者的优先序列并公示。 (2)所有租户表达对所有可调整房源的偏好序P(R)。 (3)已租房集合H′中的每个Hi指向其对应原租户Ri,空房源集合H″中的每个Hj则指向最高优先序的租户Rt。 (4)每个租户Ri指向其偏好序中排在最前端的房源。 (5)第一轮,在有限集合R-H形成的指向中,至少会形成一个“指向循环”,此时,形成的循环中的租户及其得到的房屋一起退出分配。未进入循环的申请者和房屋,则进入下一轮的分配。 (6)在余下未退出分配的租户中,如第一偏好的房源已被选走,则指向第二偏好的房子;尚未分出的每个已租房Hi仍指向其对应原租户Ri,尚未分配的每个空房源Hi则指向余下的最高优先序的租户;形成的“指向循环”中的租户和房同时退出分配。 (7)重复前一个步骤(6),直到所有人都交换完毕退出循环,匹配过程结束。 为清晰原理,我们举例如下: 假设情景与表6-1和表6-2一致,四位租户的优先序为R3,R4,R2,R1。 第一轮,租户与房源的相互偏好指向如图6-1,从图6-1中可见R3-H2是一个指向循环,所以新租户R3与空房源H2匹配并退出分配。 第二轮,R3-H2退出后的租户与房源的相互偏好指向如图6-2,从图6-2中可见R1-H4-R4-H1-R1是一个指向循环,所以新租户R4与已租房H1、原租户R1与空房源H4匹配并退出分配。 第三轮,在R1-H4-R4-H1退出后的租户与房源的相互偏好指向如图6-3,从图6-3中可见R2-H3是一个指向循环,所以新租户R2与空房源H3匹配并退出分配,分配到此结束。 图6-1 TTC调整第一轮 图6-2 TTC调整第二轮 图6-3 TTC调整第三轮 调整后的结果见表7。 在TTC机制中,通过申请者的偏好表达和房屋的反向指向,保证了原租户对其已租房的优先选择权,该权利不会因优先序先后形成对原租户的威胁,因此保证了分配中原租户的效用不减,是个人理性的机制;对每个参与者来说表达真实的偏好是占优策略,所以它是防策略的机制;在不损害其他申请者的前提下可使得其他申请者效用提高,该机制可能达到帕累托最优分配状态。 3.保全优先机制 TTC机制为公租房再分配调整提供了福利优化的方向。然而,在公租房调整实践中,参与调整的房源通常多于交换机制(可能达到成百上千),要求租户真实表达对所有房源的偏好,在偏好序的基础上再运用TTC机制形成多重匹配循环圈,才可能得到帕累托最优的资源配置结果。本文对TTC的例证也是在固定了房源和原租户数量的前提下得到的结论。事实上,这对有限理性的租户来说确实不是件容易的事,采用与其等价的保全优先机制(You request my house—I get your turn,YRMH-IGYT)机制或许是一个较好的解决方法。YRMH-IGYT机制结合了SD机制的选房特点,无须申请者同时对所有房源进行偏好排序再进行匹配,并保持了TTC机制的原租户参与调整而不承担风险的优点。其运行过程如下: (1)管理部门按照统一的规则(如随机、综合评分等)决定所有申请者的优先序列并公示。 (2)优先序排第一的申请者选择他最偏好的房源,优先序排在第二位的申请者在剩余的房源中选择他最偏好的房源,依次类推,直到新租户希望选择的房源为原租户的已租房。 (3)当(2)中的冲突发生时,若原租户在待选房序列中却尚未匹配到合适房源,则将原租户在优先序列中的排名移动到优先序列最前端,并按步骤(2)继续分配,直至无房可分或无人参与。 为清楚机制的具体流程,举例如下: 假设情景与表6-1和表6-2一致,从表6-3可以看出,当新租户Ri的优先序高于原租户R1,对∀Hj∈H-H1,有H1P(Ri)Hj,i=2,3,4,即Ri最偏爱原租户R1的已租房H1,在YRMH-IGYT机制下,当Ri依序选择原租户R1的已租房H1时,将R1的优先序提到顶部,调整优先序后分配结果及效用的变化如表6-4所示。 表6-4 YRMH-IGYT机制下的调整结果 由表6-3与表6-4比较可看出,原租户R1在YRMH-IGYT机制下,调整后的住房最低效用保持为2,且有希望调整到更为喜欢的住房。对比SD,YRMH-IGYT与TTC一样,充分考虑了原租户效用,机制中一旦出现可能使原租户效用降低的“冲突”,对原租户的“保全优先”机制便会被触发。原租户参与调整将不承担效用降低的风险,为产生调整需求的原租户提供了效用保障。因此该机制满足个人理性的条件;同时在该机制中,申请者只有表达真实偏好才是占优策略,即不能通过表达不真实的偏好使分配结果更有利于自己,因此,“保全优先”机制是防策略的。Sönmez和Ünver证明了YRMH-IGYT与改进的TTC机制的匹配结果相同,即在任何合理的优先序下,得到的分配结果都能满足“原租户的效用不减的前提下的帕累托最优”。 相比TTC机制,YRMH-IGYT机制无需租户表达对所有房源的偏好就能得到帕累托最优的分配结果,但却有执行效率不高的缺陷。以1000套房源为例,每个申请人选房时间五分钟,大约十天可选完。此外,如果申请人在五分钟时间内由于认知不全出现决策偏差,则妨碍达到效用的完美状态。 至于公平性,从表6-4也可以看出,出于保护原租户利益的考虑,有12次将原租户的优先序提到前端,其中7次有嫉妒产生,所以并不能满足优先序下无嫉妒公平的标准。 命题5:存在部分原租户的顶层交易机制(TTC)等价于YRMH-IGYT机制,均是个人理性、无策略且帕累托最优的机制,却不一定是公平的机制。 以上分析可得出,在优先序为R3,R4,R2,R1时,三种机制下调整的结果如表7。其结果表明并无一个稳定的机制能同时满足公平与效率的目标。 表7 三种调整机制在优先序为R3,R4,R2,R1时的分配结果及效用 本文对于现行公共租赁住房再分配机制的性能进行了分析,并从理论上探讨了其优化的路径,目的在于提高我国公租房再分配的公平与效率。 现行公共租赁住房再分配交换机制是一种帕累托改进的机制,存在进一步优化的空间。理论上,放松原租户的偏好表达限制,使原租户可充分表达自己的真实偏好;运用G-TTC机制寻找循环圈,集中多次两两交换或循环圈内租户同时交换,可得到帕累托最优的结果。实践中,如能引入信息系统运行G-TTC机制展开匹配工作,执行效率亦可大大提高;但当形成较大循环圈时,需要管理部门与租户的协调一致才能保证交换的顺利实施。 公租房的调整是一类更为复杂的再分配问题,难点在于原租户与新租户间公平与效率的权衡。目前将原租户与新租户分开配租的机制是既非帕累托最优亦非公平的机制。在混合配租下,保留权利的序列独裁调整机制(SD),不能保证原租户的福利不下降,是非帕累托最优的却是公平的机制。而从理论上看,TTC及其等价的YRMH-IGYT机制,均是个人理性、无策略且帕累托最优的机制,却不一定能满足无嫉妒式公平标准。尽管理论上YRMH-IGYT机制的分配结果与TTC机制相同,但实践中,前者可回避租户表达过多偏好的困境,却是以不易于信息系统自动完成、执行效率较为低下为代价的。 本文理论上分析了公租房再分配机制的种种优化路径,但实践问题远复杂于本文中四人四房的讨论;且有住房匹配实验对其的实证检验也表明:信息、房源个数、参与人数、风险偏好以及交换后的搬迁均会或多或少影响分配结果及实施效果,究竟哪种机制更合适我国公租房再分配实践,不仅需要平衡定位公平与效率的目标,更需要运用实验室实验乃至田野实验方法进行充分比较与论证。 注释 ①空房源含增量房与腾退的已租房。 ②这也是符合慎重原则的。 ③魏立佳:《从微观理论到社会实践——市场设计的最新进展综述》,《世界经济文汇》2013年第3期。 ④Shapley, Lloyd, and Herbert Scarf. “On Cores and Indivisibility.”JournalofMathematicalEconomics1,no.1 (1974): 23-37. ⑤Roth, Alvin, and A. Postlewaite. “Weak versus Strong Domination in a Market Indivisible Goods.”JournalofMathematicalEconomics, 4(1977):131-137. ⑥Ma, Jinpeng. “Strategy-proofness and the Strict Core in a Market with Indivisibilities.”InternationalJournalofGameTheory23,no.1 (1994): 75-83. ⑧Abdulkadirogˇlu, Atila, and Tayfun Sönmez. “House Allocation with Existing Tenants.”JournalofEconomicTheory88,no.2 (1999): 233-260. ⑩Sönmez, Tayfun, and M. Utku Ünver. “House Allocation with Existing Tenants: A Characterization.”GamesandEconomicBehavior69,no.2 (2010): 425-445. 责任编辑 张静 The Optimization of Public Rental Housing Redistribution Mechanism ——Based on Fairness and Efficiency Deng Hongping Lu Li (School of Economics and Business Administration, Hubei Real Estate Development Research Center, Central China Normal University, Wuhan 430079) The construction of reasonable and orderly redistribution mechanism of public rental housing is the key to the sustainable operation of it. The ways generally adopted are exchange or adjustment. The current exchange mechanism of public rental housing is one of Pareto improvement. However, increasing the number of the existing tenants’ preferences revelation and the times of pair exchange, and matching automatically by G-TTC mechanism, Pareto efficient outcome may be achieved in theory. The key issue of the adjustment mechanism of public rental housing is to achieve the balance of fairness and efficiency between existing tenants and newcomers. The current adjustment mechanism simply separates existing tenants from newcomers, which can be improved significantly. In this paper,three improved adjustment mechanisms are introduced to show that TTC and its equivalent YRMH-IGYT mechanism is Pareto efficient,individually rational, and strategy-proof; while SD mechanism may be fairer. redistribution mechanism of public rental housing; exchange; adjustment; optimization 2017-01-19 教育部人文社会科学研究规划基金项目“公共租赁住房匹配机制实验研究”(14YJAZH014)四、公共租赁住房交换机制的优化









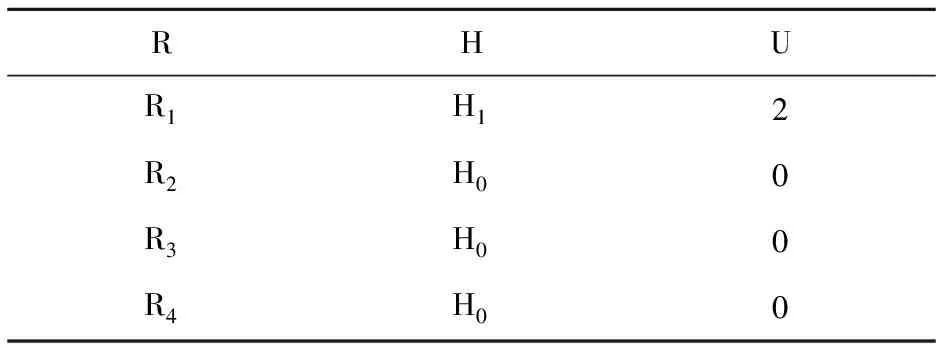
五、公共租赁住房调整机制的优化











六、结语
