低耦合度3T1R并联操作手设计与运动学分析

沈惠平 尹洪贺 邵国为 杨廷力

(常州大学现代机构学研究中心， 常州 213016)

低耦合度3T1R并联操作手设计与运动学分析

沈惠平 尹洪贺 邵国为 杨廷力

(常州大学现代机构学研究中心， 常州 213016)

基于方位特征(POC)方程的并联机构拓扑结构设计理论和机构结构降耦原理，设计了一种低耦合度能实现三平移一转动(3T1R)的SCRAR并联操作手机构。首先，阐述了该机构的组成，计算了该机构的耦合度k=1；然后，根据该机构的几何特点和运动约束，通过建立输入参数与动平台输出位姿参数间的约束方程，运用运动学序单开链法原理求解了位置正解的数值解，导出了其位置反解的解析解，用实例验证了位置正、反解的准确性；最后，基于位置反解得到了机构位置工作空间的形状与大小及Z向各截面形状，并基于Jacobian矩阵对机构奇异位形进行了分析。结果表明：该机构比H4、I4结构简单，在一组相同等效尺寸参数下其工作空间大、转动能力强。

并联机构； 方位特征集； 运动学； 三平移一转动； 低耦合度； 工作空间

引言

少自由度并联机构具有驱动构件少、工作空间大、运动耦合较弱以及制造成本低等优点。其中，对四自由度三平移一转动(3T1R)并联机构的研究、设计与应用还相对较少，但这类机构在工业生产、包装、电子产品的装配以及医疗等相关领域，应用前景广阔。

黄真等[1]基于螺旋理论，提出了一种4-URU型3T1R并联机器人；金琼等[2-3]基于方位特征输出矩阵和单开链理论，提出了一类3T1R并联机器人，并申请了一组5个3T1R并联机构的专利；黄田等[4]在H4、I4、Par4等相似机器人主体构造的基础上，发明了一种3T1R的Cross-Ⅳ型高速搬运机器人并实现产业化；刘辛军等[5]研制了一台单动平台且能够实现3T1R的X4型并联机构样机。

PIERROT等[6-7]研制了四自由度3T1R并联机器人样机，能实现高速抓取；SALGADO等[8]设计了一种新型3T1R并联操作手，给出了封闭的正反解；KIM等[9]综合了一种大工作空间的3T1R并联机构，同时建立了该机构的运动学模型；RICHARD等[10]研制了一种3T1R并联机构的样机;BRIOT等[11]提出了一种能实现3T1R的高速抓取的并联机构，建立了机构正反解模型，并对机构的工作空间进行了分析；作者团队最近又综合出一类13个3T1R新机构[12]。

以上研究对(3T1R)并联操作手的研发起到了重要的推动作用，但这些机构的耦合度较大(k=2)，因此，其运动学、动力学分析，特别是位置正解求解复杂。

本文提出一种结构比已有的H4、I4、Par4、Cross-IV、X4简单、低耦合度SCRAR并联机构，分析计算机构的耦合度；采用矢量法建立机构位置方程，并采用序单开链法的一维搜索法求得位置正解的数值解；基于导出的位置逆解解析解，对机构的工作空间进行分析；通过导出该机构的Jacobian矩阵分析机构的奇异位形。

1 3T1R并联机构的拓扑设计及结构分析

1.1 机构设计与描述

基于方位特征(POC)方程的并联机构拓扑结构设计理论[13-14 ]与机构结构降耦原理[15]，提出的低耦合度3T1R机构如图1所示[16]，它由动平台、静平台、2条RSS型无约束支链及1条混合支链(HSOC)组成；静平台上的转动副可取为R11⊥R21，R31⊥R41，而动平台上的转动副R14的轴线须平行于其法线。

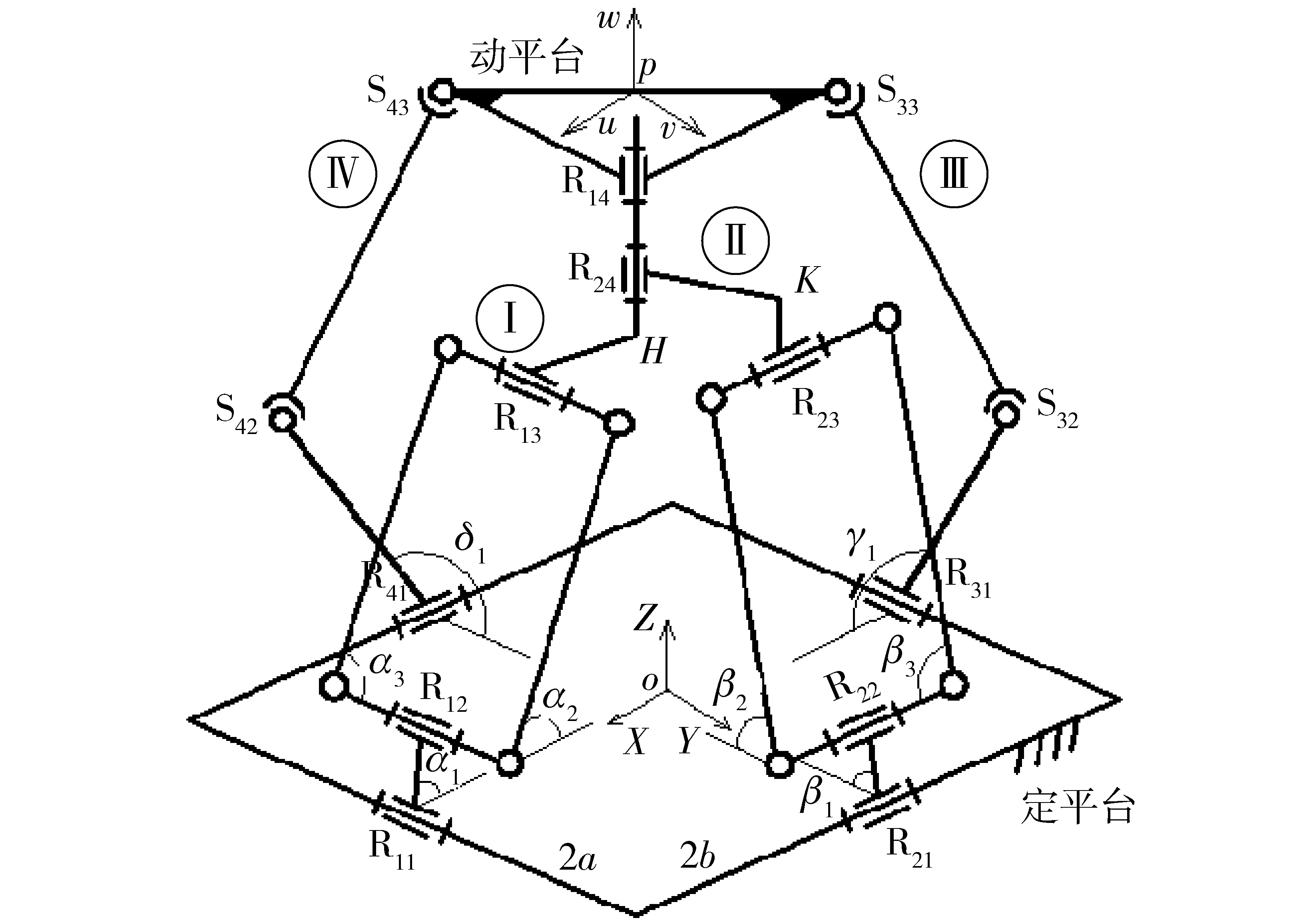
图1 3T1R并联机构简图Fig.1 Sketch of 3T1R parallel mechanism

混合支链是由2个子混合支链[17](-R∥R(-P4R-)∥R⊥R-)的末端转动副轴线重合后，又串联转动副R14构成的,其末端产生三平移一转动输出运动，而2条RSS型无约束支链产生三平移三转动输出运动，可求得该机构自由度为4[12]，当在静平台上的4个转动副为驱动副时，该机构动平台即可实现三平移以及绕R14轴线转动的输出运动。

H4、I4、Par4、Cross-IV、X4等机构，采用4条完全相同的含平行四边形的复杂支链，且耦合度k均为2，正向运动学求解复杂；而该机构仅采用2条含平行四边形的子混合支链，且耦合度k=1，因此，该3T1R机构的机械结构比已有的H4、I4、Par4、Cross-IV、X4等更简单，而正向运动学求解更简单。

为理解方便，将图1展开成平面图，如图2所示。

1.2 机构耦合度计算

为完成并联机构位置分析，需对机构进行结构分解。基于序单开链机构组成原理[14]，自由度为f的并联机构PKM可看作是由v个单开链(SOCj,j=1,2,…,v)依次连接而成，也可以认为是由f个驱动副和自由度为0的运动链组成；自由度为0的运动链又可以分解成一些基本运动链。因此，该机构可分解为

其中

式中mj——第j个SOCj的运动副数fi——第i个运动副的自由度Ij——第j个SOCj的驱动副数ξLj——第j个独立回路的独立位移方程数Δj——SOCj的约束度

机构的耦合度为

可知，该并联机构可建立含一个变量的非线性位置方程，并可通过一维搜索法求得该机构的位置正解。

2 位置正解分析

2.1 基于序SOC的机构位置正解求解基本原理

由文献[13-14]可知，单开链的约束度有正值、零、负值3种形式，因此:

2.2 机构参数标注及坐标系的建立

静坐标系oXYZ建立在静平台的中心，且X轴与R11R31连线重合，Y轴与R21R41连线重合，Z轴由右手法则确定；动坐标系puvw位于动平台斜边S43S33中点，u轴平行于直线R14S33，v轴平行于直线R14S43，w轴同样由右手法则确定。

设静平台是长和宽分别为2a、2b矩形；动平台为等腰直角三角形，直角边长为2m2。其他杆长为：lHR13=m1,lHR24=n1;lKR24=m′1,lKR23=n′1;lR14R24=q1,lR11R12=lR21R22=la；lR31S32=lR41S42=la1；lS32S33=lS42S43=lb1；4R平行四边形机构的长边长为lb。

4个主动副R11、R21、R31、R41的输入角分别为α1、β1、γ1、δ1(图1)；Ⅰ、Ⅱ支链中平行四边形平面与静平台底面的夹角分别为α2、β2，而其内摆角分别为α3、β3，动平台绕R14轴转动的转角为姿态转角γ。

该机构位置正解问题可描述为：已知主动副输入转角α1、β1、γ1、δ1，求动平台的位置(x,y,z)和姿态转角γ。假设α3为虚拟已知变量。

2.3 约束度为正值的SOC1上各运动副的求解

在I支链上，由直角坐标法可依次通过R12、R13、R24、R14点坐标，最终求得p点坐标，即

(1)

同样，由Ⅱ支链可求得p点坐标，即

(2)

由式(1)、(2)可得

(3)

其中

消去式(3)中的β2、β3则有

令

α2=2arctank1

(4)

则有

其中

得

这样由式(4)可知，α2是虚拟变量α3的函数。

2.4 约束度为零的SOC2上各运动副的求解

由Ⅲ支链，分别得S32、S33在静坐标系中坐标为

(5)

(6)

由杆长约束lS32S33=lb1，整理并化简得

A1sinγ+B1cosγ+C1=0

其中

设

γ=2arctank2

(7)

则

解得

由式(7)知，转动角γ也为虚拟变量α3的函数。

2.5 在约束度为负值的SOC3上建立位置相容方程

同样，由Ⅳ支链，分别得到S42、S43的坐标

(8)

(9)

由杆长约束lS42S43=lb1，则有

于是，通过改变α3的赋值，使f(α3)=0；再将此时得到的α3代入式(1)，即可得到p(x,y,z)，代入式(7)，即可得姿态角γ。

综上，上述各运动副的位置求解可按图3所示的流程进行求解。

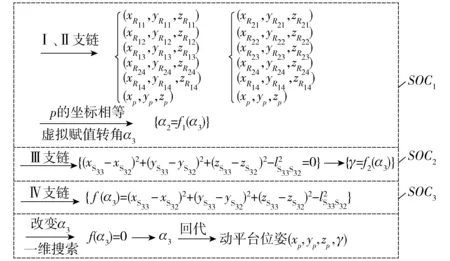
图3 机构位置正解的流程图Fig.3 Flow chart of forward position solution

3 位置逆解

该机构的反解问题可描述为：已知动平台的位置(x,y,z)及姿态角γ，求主动副输入转角α1、β1、γ1、δ1。

3.1 求主动副R11的输入角α1

对I支链，由式(1)可得

(10)

(11)

z=lasinα1+lbsinα3sinα2+q1+n1

(12)

由式(11)可得

由式(10)～(12)得

(P1+lacosα1)2+(P2-lasinα1)2=P3

其中

整理可得

P4+P5cosα1+P6sinα1=0

(13)

其中

令

ta=tan(α1/2)

(14)

解得

3.2 求主动副R21的输入角β1

对Ⅱ支链，运用同样的方法，由式(2)可得

β1=2arctantb

(15)

其中

3.3 求主动副R31的输入角γ1

由Ⅲ支链杆长约束lS32S33=lb1，及式(10)～(12)，并整理可得

P14+P15cosγ1+P16sinγ1=0

其中

令

γ1=2arctantc

(16)

则

解得

3.4 求主动副R41的输入角δ1

由Ⅳ支链上的杆长约束lS42S43=lb1，并整理得

P19+P20cosδ1+P21sinδ1=0

令

δ1=2arctantd

(17)

则

解得

综上可知，该机构存在24=16组位置反解。

4 实例验算

4.1 正解算例

为便于性能比较，参照H4、I4机器人的一组典型的结构尺寸参数[18]，该机构取相同等效参数如表1所示。

表1 机构的尺寸参数Tab.1 Structure parameters of PM cm

给定两组主动输入角：①α1=138.616°；β1=127.913°；γ1=117.852°；δ1=131.396°。②α1=138.059°；β1=136.691°；γ1=146.064°；δ1=146.855°。

通过一维搜索，运用式(1)、(7)可求得4组实数正解，如表2所示。

4.2 逆解算例

将表2中①正解中的No.2数据，代入逆解式(14)～(17)中，可得16组实数反解(略),其中，一组反解为:α1=138.617°;β1=127.915°;γ1=117.852°;δ1=131.396°。

可知，它与给定的第①组输入角一致，故认为正反解求解正确。

表2 3T1R机构位姿正解的数值解Tab.2 Numerical forward solutions of PM

5 工作空间和转动能力分析

5.1 工作空间分析

运用边界值搜索法求解机构的工作空间的思路是：基于机构的位置逆解，查找该工作空间内所有满足杆长约束、转角约束、干涉约束的点。给定空间内的点对应的驱动角α1、β1、γ1、δ1和内摆角α3、β3，若满足约束条件，则该点在工作空间内，否则在工作空间外。

当取表1所示的尺寸参数时，空间三维搜索范围为：0≤Z≤1 200，-π≤θ≤π，0≤ρ≤1 000(θ、ρ分别为柱坐标系中搜索角度和搜索半径)；约束条件：-π≤α1(β1,δ1,θ1)≤π。利用Matlab求得的工作空间的形状如图4所示，其Z轴截面图如图5所示。

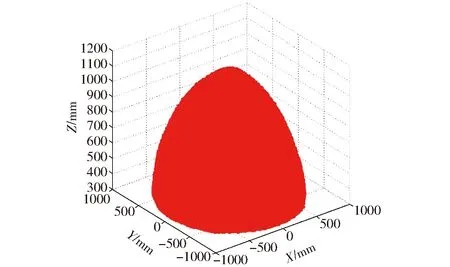
图4 工作空间三维立体图Fig.4 Three-dimensional workspace of PM

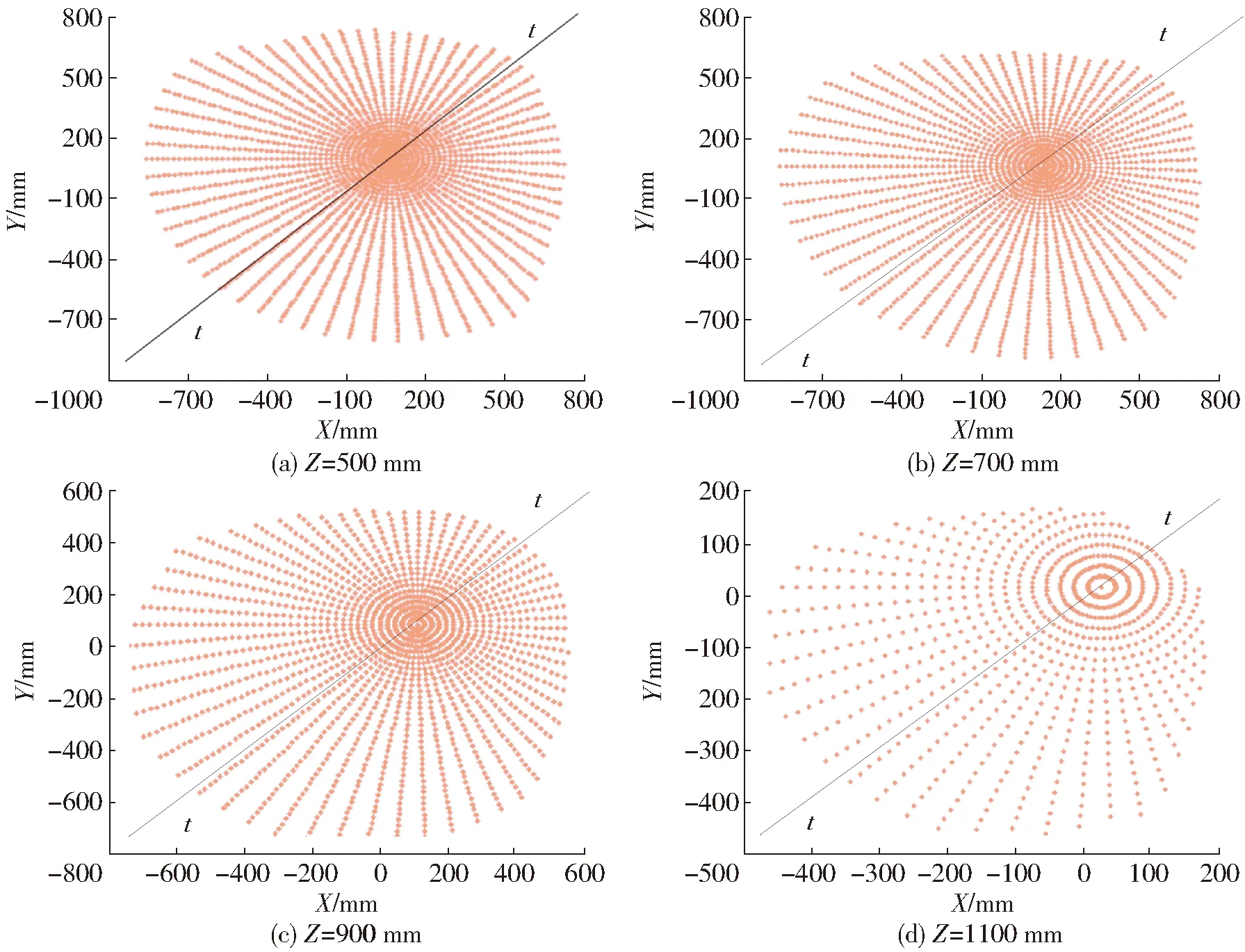
图5 工作空间Z轴截面图Fig.5 Section views of Z axis

由图4和图5可知：

(1)机构的工作空间较大，边界较光滑，且整个工作空间连续、无空洞。

(2)机构工作空间及其Z轴截面图，关于t-t线基本对称。

(3)随着Z的增加,截面面积逐渐变小，边界趋于光滑，当Z∈[500 mm，1 100 mm]时,工作空间对称性较好。

(4)在不考虑运动副转角约束、连杆干涉，以及相同参数及搜索范围得的条件下，该机构工作空间均比I4R(H4)、CrossIV-3大，具体如下：

①引用文献[18]的相应参数，给定搜索范围:0≤ρ≤1 000、500 mm≤z≤1 150 mm，计算出I4R的工作空间体积为 6.167×108mm3，而该机构为7.694×108mm3，因此，该机构工作空间体积比I4R机器人增加了24.76%。

②引用文献[19]的相应参数，给定搜索范围:0≤ρ≤1 000、766 mm≤z≤1 016 mm，CrossIV-3的工作空间体积为4.427×108mm3,而该机构为5.089×108mm3，因此，该机构工作空间体积相比CrossIV-3增加了14.95%。

5.2 转动能力分析

转动能力[20]分析是评估并联机构转动角度能够到达范围的大小。

以下取相同高度Z=1 000 mm，分别计算本文机构、H4机构在X-Y平面上各点的转角最大值γmax、最小值γmin的分布，如图6所示。

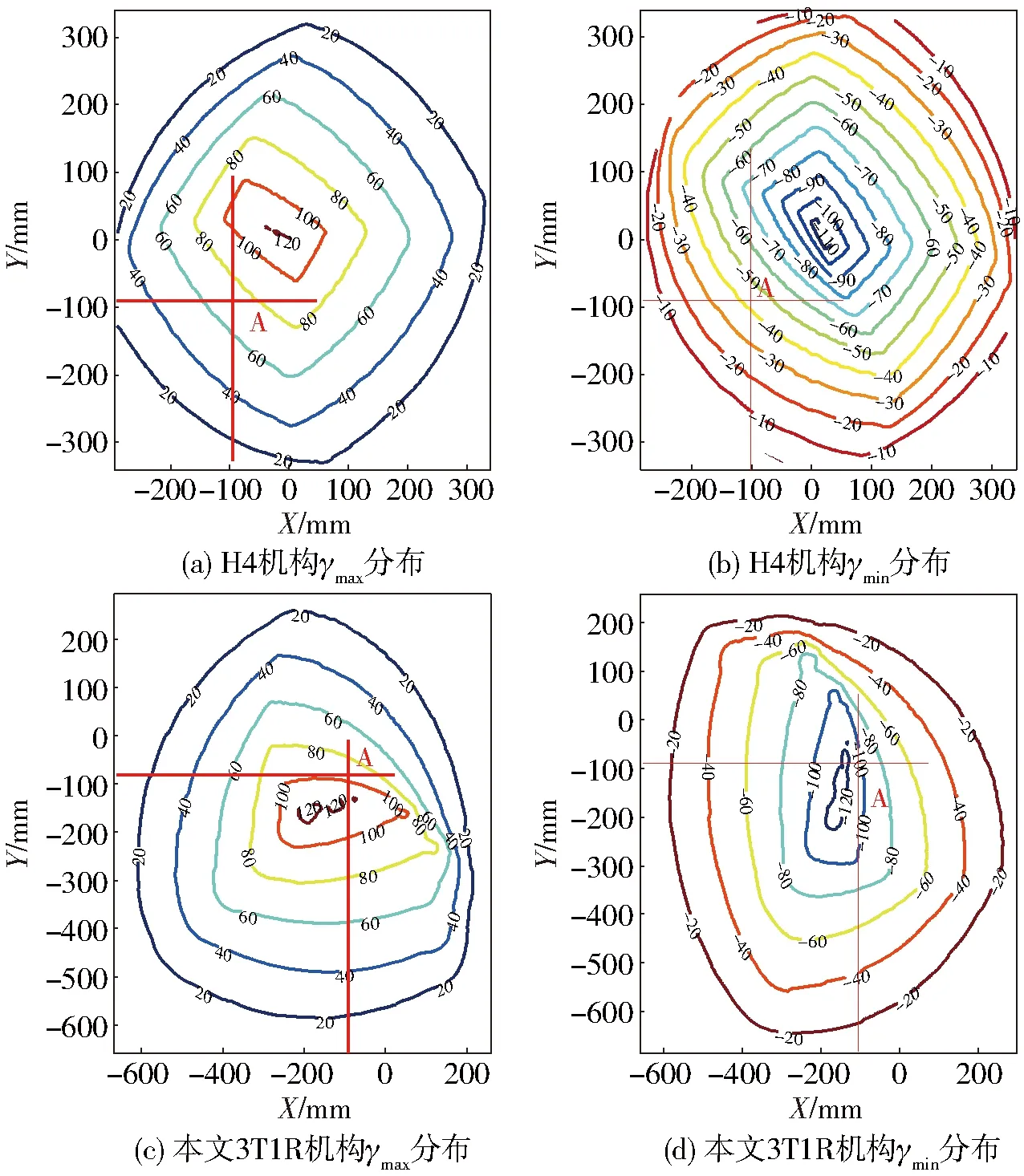
图6 本文3T1R机构与H4机构的转动能力比较Fig.6 Comparisons of rotational capacity between 3T1R and H4 PM

对比图6a和图6c，本文机构γmax∈[0°,120°]，H4的γmax∈[0°,120°]；对比图6b和图6d，本文机构γmin∈[-120°,0°]，H4的γmin∈[-110°,0°]。因此，本文提出的机构动平台转角范围比H4机构大。

进一步，在机构工作空间内取一点，例：A点，其坐标A(-100，-90，1 000)，H4机构的转角范围是[-50°,70°],本文机构的转角范围是[-100°,100°]，比H4机构大了40%。因此，该机构动平台可以无需特殊转角放大装置，便可获得较大的转角范围。

6 奇异位形分析

6.1 基本原理及方法

当约束方程线性相关，或者说机构在某位形下失去一个或者多个方向上的约束时，机构处于位形奇异状态。因此，可通过检验约束方程的雅可比矩阵是否行满秩，来判断约束方程的相关性。

R13点坐标，可同时由以下2个矢量方程

lOR11+lR11R12+lR12R13=lOR13lOO′+lO′R13=lOR13

得到

(18)

同样，点S43、S33、R23坐标也可得到，即有

(19)

(20)

(21)

其中，γ2、γ3与γ4及γ5、γ6与γ7，分别为S32S33杆、S42S43杆与静坐标系X、Y、Z轴的夹角。

对式(18)～(21)化简整理，然后等式两边分别对时间t求一阶导数得

(22)

(23)

(24)

(25)

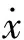
JpV=Jqω

(26)

其中

令det(Jp)=0，可得Jp矩阵行列式解的集合A为

A={tanα2+tanβ2+2tanγ2=0}

(27)

令det(Jq)=0，而Jq矩阵行列式解的集合B为

B=B1∪B2∪B3∪B4

其中

(28)

(29)

(30)

(31)

6.2 奇异位形分析

(1)第一类奇异：矩阵Jp奇异而矩阵Jq非奇异，即det(Jp)=0且det(Jq)≠0。

此时，机构处于工作空间边界或者位置反解数目发生变化时的位形。对于该机构而言，即3个从动角满足关系式(27)时，即发生这类奇异。

(2)第二类奇异：即det(Jq)=0且det(Jp)≠0。

图7 第二类奇异位形图Fig.7 Sketches of the second kind of singularity

此时，尽管驱动杆被锁定，机构的动平台仍具有一定自由度，此时机构将失去刚度，无法承受任何载荷。对本机构而言，满足式(28)～(31)中的任意一个式子，即发生该类奇异，如图7所示(也即当4条支链中任意一条支链处于拉直共线或重叠共线时)。

(3)第三类奇异：即det(Jp)=0且det(Jq)=0。

这种奇异位形只有当上述第一、二类奇异同时发生时才会产生，此时，机构将失去自由度、原有的运动特性。

7 结论

(1)提出了一种低耦合度(k=1)的四自由度3T1R并联机构，该机构在结构上具有较好的对称性, 与H4、Cross-IV、X4机构相比，更为简单、制造装配更为容易。

(2)基于序单开链法原理，建立了机构位置正解求解模型：建立一个含1个变量的杆长约束方程，并用一维搜索求解，得到了机构的全部实数位置正解。该方法物理意义明确，计算简便；同时利用Matlab软件验证了正反解算法的正确性。

(3)基于位置反解的机构工作空间分析和转动能力分析表明：在一组相同等效典型的结构参数下，该机构工作空间相比I4(H4)、CrossIV-3 分别提高24.76%、14.95%,转动能力也有提高。

(4)求解了机构的雅可比矩阵，并据此探讨了机构的三类奇异位形发生条件及其位置。

1 黄真，赵铁石，李秦川.空间少自由度并联机器人机构的基础综合理论[C]∥第一届国际机械工程学术会议，2000:90-91. HUANG Zhen,ZHAO Tieshi,LI Qinchuan.A screw approach to deficient-DOF spatial parallel mechanisms constructing and its application[C]∥The First International Conference on Mechanical Engineering,2000:90-91.(in Chinese)

2 金琼, 杨廷力, 刘安心,等. 基于单开链单元的三平移一转动并联机器人机构型综合及分类[J]. 中国机械工程, 2001, 12(9):1038-1043. JIN Qiong，YANG Tingli, LIU Anxin, et al. Kinematics analysis of a parallel pneumatic and hydraulic linkage based on single-opened-chain[J].China Mechanical Engineering, 2001,12(9):1038-1043. (in Chinese)

3 杨廷力，金琼，罗玉峰, 等.用于虚轴机床与机器人等的一类(三平移一转动)并联机构：中国， 200310106012.4[P].2004-09-15.

4 黄田, 赵学满, 梅江平,等. 一种具有三维平动一维转动的并联机构:中国,202528189U[P]. 2012-11-14.

5 刘辛军，谢福贵，王立平，等．一种可实现SCARA运动的四自由度单动平台并联机构:中国，201210435375.1[P].2013-02-13．

6 PIERROT F, NABAT V, COMPANY O, et al. Optimal design of a 4-DOF parallel manipulator: from academia to industry[J]. IEEE Transactions on Robotics, 2009, 25(2):213-224.

7 COMPANY O, MARQUET F, PIERROT F. A new high-speed 4-DOF parallel robot synthesis and modeling issues[J]. IEEE Transactions on Robotics & Automation, 2003, 19(3):411-420.

8 SALGADO O, ALTUZARRA O, PETUYA V, et al. Synthesis and design of a novel 3T1R fully-parallel manipulator[J]. Journal of Mechanical Design, 2008, 130(4):137-139.

9 KIM S M, KIM W, YI B J. Kinematic analysis and optimal design of a 3T1R type parallel mechanism[C]∥IEEE International Conference on Robotics and Automation, 2009:2199-2204.

10 RICHARD P L, GOSSELIN C M, KONG X. Kinematic analysis and prototyping of a partially decoupled 4-DOF 3T1R parallel manipulator[J]. Journal of Mechanical Design, 2007, 129(6):611-616.

11 BRIOT S, BONEV I A. Pantopteron-4: a new 3T1R decoupled parallel manipulator for pick-and-place applications[J]. Mechanism & Machine Theory, 2010, 45(5):707-721.

12 YANG Tingli，LIU Anxin，SHEN Huiping, et al. Topological structure synthesis of 3T1R parallel mechanism based on POC equations[C]∥2016 Proceedings of 9th International Conference on Intelligent Robotics and Applications, ICIRA, 2016:147-161.

13 杨廷力.机器人机构拓扑结构学[M].北京：机械工业出版社, 2004.

14 杨廷力，刘安心，罗玉峰,等.机器人机构拓扑结构设计[M]. 北京：科学出版社,2012.

15 SHEN Huiping，YANG Liangjie，MENG Qingmei,et al.Topological structure coupling-reducing of parallel mechanisms[C]∥2015 IFToMM Wold Congress，2015．

16 沈惠平,强恒存,邵国为,等. 一种低耦合度三运动副动平台的三平移一转动并联机器人机构:中国,201610141468.1[P].2016-03-14.

17 廖明,刘安心,沈惠平,等.并联机构方位特征集的符号推导方法[J/OL].农业机械学报,2016,47(3):395-404. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160356&flag=1.DOI：10.6041/j.issn.1000-1298.2016.03.056. LIAO Ming,LIU Anxin,SHEN Huiping, et al.Symbolic derivation of position and orientation characteristics of parallel mechanism[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2016,47(3):395-404.(in Chinese)

18 刘平松. I4型并联机器人全域性能及其优化研究[D].南京：南京理工大学, 2013. LIU Pingsong.Global performance and optimization of I4R parallel robot[D].Nanjing:Nanjing University of Science and Technology,2013.(in Chinese)

19 李玉航, 梅江平, 刘松涛,等. 一种新型4自由度高速并联机械手动力尺度综合[J]. 机械工程学报, 2014,50(19):32-40. LI Yuhang, MEI Jiangping, LIU Songtao,et al.Dynamic dimensional synthesis of a 4-DOF high-speed parallel manipulator[J].Journal of Mechanical Engineering 2014,50(19):32-40.(in Chinese)

20 朱小蓉,宋月月,孙晨,等.2RRUR-2RSS并联机构结构特性与运动学分析[J/OL].农业机械学报,2016,47(12):408-415. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20161252&flag=1.DOI：10.6041/j.issn.1000-1298.2016.12.052. ZHU Xiaorong,SONG Yueyue,SUN Chen, et al.Structural characteristics and kinematic analysis for novel 2RRUR-2RSS parallel mechanism[J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2016,47(12):408-415.(in Chinese)

Design and Kinematics Analysis of a Novel 3T1R Parallel Manipulator with Lower Coupling Degree

SHEN Huiping YIN Honghe SHAO Guowei YANG Tingli
(ResearchCenterforAdvancedMechanismTheory,ChangzhouUniversity,Changzhou213016,China)

Comparing with the 3-DOF Delta mechanism, the 4-DOF parallel mechanisms which can achieve SCARA motion (i.e., three translations and one rotation) have their own complex topological structures with coupling degreek=2, which results in the higher complexity level of solutions for forward kinematics and dynamics. According to the design theory for parallel mechanisms (PMs) based on position and orientation characteristic (POC) equation and the principle for the coupling degree reducing, a novel 4-DOF SCARA type parallel manipulator with lower coupling degree ofk=1 was proposed. Firstly, the structure of the 4-DOF SCARA PM was introduced and the coupling degree of the mechanisms was calculated as beingk=1. Secondly, the direct position and the inverse kinematics problem of the mechanism was solved by using the modeling methods based on the ordered SOC unit, and the positive and inverse solutions were verified by numerical methods using Matlab. Furthermore, the workspace of the mechanism was analyzed based on inverse solutions formula. Meanwhile, rotation ability of the PM was analyzed. Finally, the singularity analysis of the mechanism was also performed based on Jacobian matrix, from which three kinds of singular conditions were obtained. The results showed that the manipulator had a simpler mechanical structure and larger workspace and rotation ability than H4 or Cross-Ⅳ under the same set of structural parameters. The research provided a theoretical base for its kinematics and dynamics and optimal design of this manipulator.

parallel mechanism; position and orientation characteristic set; kinematics; 3T1R; lower coupling degree; workspace

2016-09-16

2016-10-31

国家自然科学基金项目(51475050、51375062)和江苏省重点研发计划项目(BE2015043)

沈惠平(1965—)，男，教授，博士生导师，主要从事机构学和并联机构研究，E-mail: shp65@126.com

10.6041/j.issn.1000-1298.2017.05.052

TH112

A

1000-1298(2017)05-0405-08