基于博弈论赋权的灌溉用水效率GRA-TOPSIS评价模型

刘 东 龚方华 付 强 FAIZ M Abrar 李天霄 崔 嵩

(1.东北农业大学水利与土木工程学院， 哈尔滨 150030； 2.农业部农业水资源高效利用重点实验室， 哈尔滨 150030)

基于博弈论赋权的灌溉用水效率GRA-TOPSIS评价模型

刘 东1,2龚方华1付 强1FAIZ M Abrar1李天霄1崔 嵩1

(1.东北农业大学水利与土木工程学院， 哈尔滨 150030； 2.农业部农业水资源高效利用重点实验室， 哈尔滨 150030)

在构建区域灌溉用水效率综合评价指标体系的基础上，运用博弈论(Game theory，GT)思想将层次分析法(Analytic hierarchy process，AHP)所得主观权重与改进熵值法(Improved entropy value method，IEVM)所得客观权重进行综合集成以获取组合权值，并将灰色关联分析(Gray relation analysis，GRA)与逼近理想解排序(Technique for order preference by similarity to ideal solution，TOPSIS)相结合，以三江平原10个大型灌区为例进行验证，对区域灌溉用水效率作综合评价。采用Spearman等级相关系数检验灌溉水有效利用系数排序与GRA-TOPSIS法排序，得到的相关系数高达0.863，且GRA-TOPSIS法、GRA法、TOPSIS法对同一灌区综合排序的位次相差均不超过2，表明评价结果具有合理性和一致性；GRA-TOPSIS法所得综合值的极差为0.343，变异系数为0.267，均高于单独使用GRA法或TOPSIS法的极差与变异系数，更有利于对灌区灌溉用水效率进行辨识分区。此外，根据目标层与准则层排序差异度将灌区分为3类，辨识各灌区灌溉用水效率主控因子，对区域灌溉用水效率发展策略的制定具有参考价值。

灌溉用水效率； 大型灌区； 博弈论； 灰色关联分析； 逼近理想解排序； 综合评价

引言

灌溉用水效率综合表征不同尺度灌溉技术水平、灌溉工程状况、用水管理制度等，是正确评估灌溉水有效利用情况及存在问题，衡量灌区节水改造成效的重要基础[1]。准确客观量化地评价区域灌溉用水效率，是节水灌溉的重要研究课题[2-3]，对推行最严格的水资源管理制度意义重大[4]。大型灌区灌溉用水效率的评估关系到水资源高效利用与国民经济发展，是灌溉用水效率综合评价的首要任务和重中之重[5]。

迄今为止，国内外众多专家学者已对灌溉用水效率评价体系与评价方法进行了研究。MOLDEN[6]通过水分生产率、水分消耗率和水分有益消耗率的水平衡框架来研究灌溉用水效率；YILMAZ等[7]运用数据包络分析法对灌区灌溉技术效率进行了研究；雷贵荣等[8]和刘军等[9]先后利用随机前沿生产函数计算灌溉用水技术效率和生产效率；李绍飞等[10]在提出不同尺度灌区指标分级标准的基础上，运用模糊综合评价模型对灌溉用水效率进行评价。李浩鑫等[4]将主成分分析与Copula函数结合对灌溉用水效率进行评价。然而，现有研究大多基于少量指标数据分析，缺乏针对灌溉用水效率相对完备的综合评价指标体系及普适易用的评价方法[11]。

在灌溉用水效率综合评价过程中指标数据有限的情况下，通过TOPSIS法进行运算时，存在数据波动变化大、难以寻求其典型分布规律的缺陷[12]，而灰色关联分析研究的正是“贫信息”的不确定性系统[13]。GRA-TOPSIS耦合模型能在考虑评估对象在多维空间中实际距离的同时顾及其在形状态势上的关联度[14]。

前人[12,15]大多只提出GRA-TOPSIS模型并将其应用于实例来证实其合理性，鲜有表征该模型优越性的实例论证。本文以黑龙江省三江平原10个大型灌区为例进行研究，验证GRA-TOPSIS法在大型灌区灌溉用水效率综合评价中的可行性与优越性，并以此模型辨析灌溉用水效率主控因子。

1 区域灌溉用水效率综合评价指标体系

广义的灌溉用水效率包括灌溉用水的配置效率与经济效率，可用灌溉水传输耗散比、农作物投入产出比等来刻画[16]。鉴于灌溉用水效率既可从各类用水指标中体现，又与工程设施状况、灌区管理水平密切相关，遵循指标选取、体系构建的科学性、可比性、代表性、综合性等原则[17-18]，借鉴前人已建体系[10,18]，参照从事农业用水研究的专家、灌区管理人员的意见与建议，兼顾指标数据来源的可靠性与有限性，最终构建区域灌溉用水效率综合评价指标体系，如图1所示，图中各指标含义见表1。

图1 区域灌溉用水效率综合评价指标体系Fig.1 Comprehensive evaluation indicator system of regional irrigation water use efficiency

2 区域灌溉用水效率GRA-TOPSIS模型

2.1 指标预处理

假设有m个灌区，每个灌区包含n个评价指标，建立决策矩阵A=(xij)m×n(xij为i灌区j指标的原始数据)。

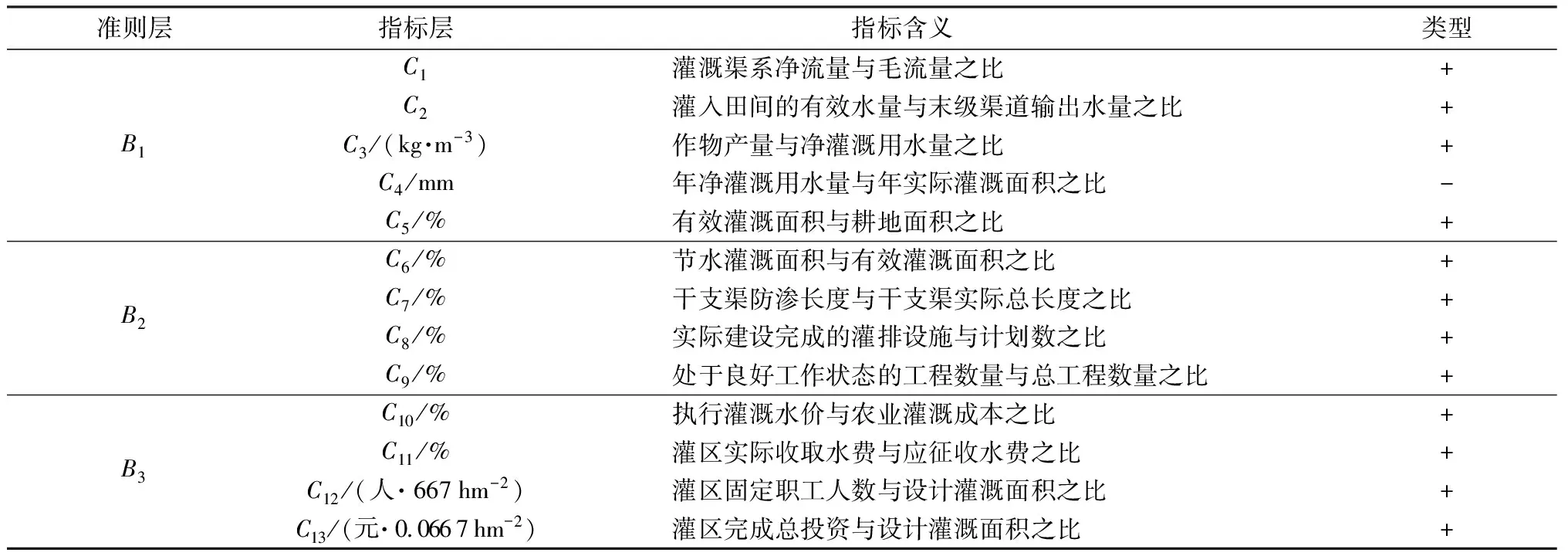
表1 灌溉用水效率综合评价指标涵义Tab.1 Connotation of comprehensive evaluation indicators of irrigation water use efficiency

注：指标含义参照SL 56—2013《农村水利技术术语》。

为消除指标类型与量纲对评判的影响，便于指标比较，需对xij进行规范化处理。本文选用极值处理法作为预处理方法，因其具有平移无关性、差异比不变性、区间稳定性等多种有益性质[19]，具体表达式为

(1)

由式(1)可得规范化矩阵B=(yij)m×n(yij为i灌区j指标的规范化数据)。

2.2 博弈论集化权重模型

2.2.1 层次分析法定权

AHP法具体步骤可参照文献[20-22]，此处不再赘述。

2.2.2 改进熵值法定权

熵值法是依据指标的变异信息熵来确定权重的一种客观赋权法[23]，步骤如下：

(1)求yij的特征比重pij。为避免pij得值为零[24]，对yij统一加0.1，以此改进熵值法[25]，使其具有更广泛的可适性与科学性。

(2)

(2)求j指标的信息熵ej。

(3)

(3)求j指标的权重wj。

(4)

2.2.3 博弈论组合赋权

指标权重在多因子系统综合评价中占重要地位[19]，本文兼顾主、客观赋权的优点，运用博弈论集化模型[26]对指标进行组合赋权，方法如下：

用L种不同赋权法对指标分别赋权，构造出基础权重向量集uk={uk1,uk2,…,ukn}(k=1,2,…,L)，记这L个不同向量的任意线性组合为

(5)

式中u——权重集的一种可能的权重向量αk——线性组合系数

运用博弈论思想优化L个线性组合系数αk，旨在使u与各个uk的离差极小化，即

(6)

式(6)的最优化一阶导数条件可转换为方程组

(7)

根据式(7)求得(α1,α2,…,αL)后将其用改进的归一化公式[27]处理，即

(8)

得最满意的综合权重向量为

(9)

2.3GRA-TOPSIS法基本步骤

(10)

式中zi(j)——各待估灌区的zij值

(3)求各待估灌区与正理想解集的灰色关联系数ri(j)。

(11)

式中λ——分辨系数

λ常取定值0.5[15,28]，但如此取值会造成参考、比较序列无论如何变化，相应的关联系数下限值均为0.333 3的不合理现象[29]。λ应在充分体现系统各要素对关联度影响的同时起稳健抗干扰的作用，故应该是绝对动态、相对静态的。参照文献[30]确定分辨系数λ的方法，结合实际研究数据得λ=0.3。

由式(11)得到灰色关联系数矩阵为R=(ri(j))m×n。

(12)

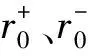
(13)

(6)求各灌区灰色相对贴近度T。

(14)

T决定各灌区的排序，T大者排序靠前，反之则靠后。

3 实例分析

3.1 研究区概况

三江平原地处黑龙江省东部，北起黑龙江，南抵兴凯湖，西倚小兴安岭，东迄乌苏里江，地理坐标45°01′05″～48°27′20″N、130°13′01″～135°05′26″E[31]，行政区包括鸡西市、鹤岗市、双鸭山市、依兰县等23个市县，总面积1.089×107hm2，占黑龙江省总面积的24%[32]，耕地面积3.78×106hm2，占全省耕地总面积的30%[33-34]。三江平原地势低平，气候适宜，土壤肥沃，水源丰富，耕地集中连片，是我国重要的商品粮生产基地和粮食储备基地。科学评价三江平原大型灌区灌溉用水效率可为区域节水灌溉项目决策及灌溉管理提供参考依据[35]，对建好中国最大的灌区——三江平原灌区，并将其打造成稳固优质的粳稻生产基地具有重要的现实意义。

3.2 数据来源

通过对三江平原大型灌区的实地调研，本文以倭肯河、引汤、悦来、鸡东、梧桐河、幸福、兴凯湖、蛤蟆通、江川、龙头桥10个大型灌区为样本，统计了2013年上述灌区各项指标数据。样点灌区在三江平原上的空间分布如图2所示。

本次研究数据主要来自黑龙江省样点灌区基本资料调查表、黑龙江省灌溉信息网，并通过《黑龙江省水利建设综合年报》数据进行核实、校正及增补。指标层中C1、C2、C3指标数据为统计数据，其余指标数值根据表1中指标涵义由统计数据计算求得。此外，各灌区灌溉水有效利用系数来自黑龙江省灌溉管理中心提供的测算分析结果。

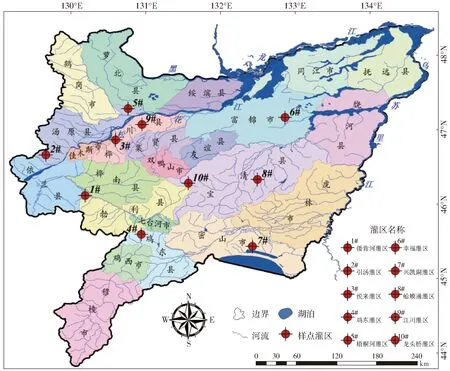
图2 样点灌区与研究区示意图Fig.2 Distribution of sample irrigation districts in Sanjiang Plain

3.3 结果与分析

运用博弈论思想将AHP所得主观权重与IEVM所得客观权重综合集成并对各指标进行组合赋权，结果见表2。

主观赋权和客观赋权各有其优缺点，单独使用某类赋权法均会导致评价结果存在一定局限性[36-37]。由表2可知，不同的计算原理及侧重点致使AHP与IEVM所得权重分配差异性显著，而GT能协调此类矛盾，如专家们给出C1指标的权重高达0.196，而IEVM求得C1的权重仅为0.060，GT优化取权重为0.148。由此可知，陈加良[26]以Nash均衡为调解目标提出的GT集化模型可最小化各基本权重与可能权重之间的偏差，从而获取更为全面、科学、可靠的权值[38]。

由GRA-TOPSIS模型求得2013年10个大型灌区的欧氏距离与灰色相对贴近度，依据贴近度从小到大的顺序排列灌区，如图3所示。对图3中的贴近度进行线性拟合，拟合决定系数R2高达0.973，验证了GRA-TOPSIS模型所得评价值分布均匀合理。

表2 博弈论所赋各指标集化权重Tab.2 Combinational index weights obtained by using game theory

本文还结合各灌区的灌溉用水有效利用系数，将GRA-TOPSIS评价法与GRA法以及TOPSIS法的评价计算结果进行对比分析，结果如表3所示。需要指出的是，为了增强对照性，这3种评价法所用的权重为表2中的博弈论权重，数据预处理方法均为极值标准化法。

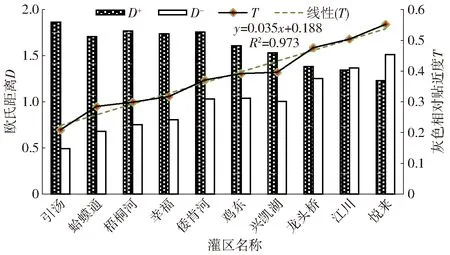
图3 2013年10个大型灌区欧氏距离与灰色相对贴近度Fig.3 Euclidean distance and gray relative closeness degree of ten large-scale irrigation districts in 2013

由表3可知，GRA-TOPSIS法、GRA法、TOPSIS法对同一灌区最终所得灌溉用水效率综合排序的位次相差均不超过2。同时，利用Spearman等级相关系数检验法来检验GRA-TOPSIS法与其他2种方法的关联程度，得相关系数分别为0.952和0.927 (P<0.01)，表明这3种评价法关联度极高，即所得评价结果一致性令人满意，也说明了GRA-TOPSIS评价法计算结果的合理性。

同时，灌溉水有效利用系数作为评价节水灌溉成效、用水管理水平、灌溉工程质量的一项综合指标，在很大程度上能反映灌区灌溉用水效率[4,39]，全国范围内也普遍用它来量化灌溉用水水平。由Spearman等级相关系数检验法可得灌溉水有效利用系数排序与GRA-TOPSIS、GRA、TOPSIS这3种方法的评价排序之间的相关系数分别为0.863 (P<0.01)、0.742(P<0.05)、0.736(P<0.05)，显然运用GRA-TOPSIS评价法比单独使用GRA法或TOPSIS法更具优势，更能综合客观地反映与用水指标、灌区工程状况、用水管理水平相适应的灌溉用水效率。

表3 3种评价法结果对比分析Tab.3 Comparative analysis of results of GRA-TOPSIS, GRA and TOPSIS

此外，GRA-TOPSIS、GRA、TOPSIS这3种方法所得灌溉用水效率综合评价值的极差分别为0.343、0.244、0.313，变异系数分别为0.267、0.103、0.190；灌溉水有效利用系数的极差和变异系数分别为0.059和0.047。极差和变异系数越大说明综合评价值分辨水平、离散程度越高，对区分不同灌区灌溉用水效率、划分灌溉用水效率等级具有更强的适宜性。显然，GRA-TOPSIS法所得综合值的极差和变异系数均比GRA法、TOPSIS法大，可知其所得综合值较其他2种方法分布更均匀合理，且相邻排序间综合值差异更明显，更有利于直观地区分各灌区灌溉用水效率水平；而灌溉水有效利用系数的极差和变异系数都非常小，分辨水平极低，并不适于直接评价灌区灌溉用水效率，这也正是用各种算法、模型进行灌溉用水效率综合评价的价值所在。

3.4 灌溉用水效率主控因子辨识

辨析区域灌溉用水效率主控因子可为灌区提升灌溉用水效率提供更具针对性和说服力的决策支持。解构图1中的评价指标体系，依据指标原始数据(考虑了指标类型)对指标层各指标排序，运用GRA-TOPSIS法对准则层三要素(B1用水指标、B2工程状况、B3管理水平)分别进行排序，与综合排序进行对比分析，结果如表4所示，并以图4来可视化表达综合排序与准则层排序的空间分布。

依据总排序与准则层排序的差异度将灌区分为3类：Ⅰ类灌区准则层排序与综合排序差异度小于5，有梧桐河、兴凯湖、江川三大灌区，此类灌区表现为各维度建设水平与总体水平相当，在制定灌溉用水效率发展策略时需注意准则层三要素的协同性，需在用水指标、工程状况、管理水平各环节全方位采取改善措施。Ⅱ类灌区准则层排序与综合排序差异度在5～9之间，有引汤、悦来、鸡东、幸福、蛤蟆通五大灌区，此类灌区需要依靠指标层排序来辅助灌区建设方略的拟定。相对达标指标的标准如下：对于排序处于前5位的准则层，以指标排序劣于该准则层排序不超过2为宜；对于排序位于后5位的准则层，以指标排序优于该准则层2个位次及以上为宜。例如引汤灌区B1排序为10，属于后5位，则其B1层下的达标指标排序不得劣于8，即只有C1、C4达标，同理可知，其B2层下C7、C8达标，B3层下C11、C12、C13达标，故该灌区提升灌溉用水效率需优先发展C2、C3、C5、C6、C9、C10指标。同理可得，悦来灌区需注意C3、C4、C9指标，鸡东灌区需优化C3、C4、C9、C10指标，幸福灌区应提升C2、C5、C8、C10、C11、C12、C13指标，蛤蟆通灌区应加强C1、C6、C7、C9、C11、C12指标。Ⅲ类灌区准则层排序与综合排序差异度大于9，有倭肯河、龙头桥两大灌区，此类灌区表现为综合排序对某一准则层响应明显，只需改善相应准则层即可实现灌溉用水效率大幅提升，如倭肯河灌区应注重推广节水灌溉、增加渠道防渗衬砌率、提升灌区工程配套及完好率等工程问题，而龙头桥灌区则应着重改善管理水平，如加强资金投入力度、人才支持，并适当增加水费实收率、灌溉成本水价以提高农户节水意识。

4 结论

(1)建立了普适完整的区域灌溉用水效率综合评价指标体系，运用博弈论思想将主客观权重综合集成，尝试将GRA-TOPSIS法应用于灌溉用水效率综合评价。

表4 各灌区综合排序、准则层排序和指标层排序Tab.4 Rankings of target layer, criterion layer and indicator layer of each irrigation district

注：差异度指准则层排序与综合排序之差的绝对值之和，如倭肯河灌区差异度=|6-1|+|6-10|+|6-4|=11。

图4 目标层与各准则层排序空间分布图Fig.4 Spatial distribution of target layer and criterion layer ranks of each irrigation district

(2)在实例中将GRA-TOPSIS法与GRA法、TOPSIS法比较，结果表明GRA-TOPSIS法所得排序与灌溉水有效利用系数排序的Spearman等级相关系数为0.863，所得综合值的极差为0.343，变异系数为0.267，这3个评价参数方面GRA-TOPSIS法均占优势，表明GRA-TOPSIS法比单独使用GRA法或TOPSIS法更具优越性。

(3)解构评价指标体系，依据目标层与准则层的排序差异度将灌区分为3类，并适时引入指标层排序来针对性地分析各灌区灌溉用水效率主控因子，可为各灌区制定适宜的灌溉用水效率发展策略提供参考依据。

1 崔远来，谭芳，郑传举．不同环节灌溉用水效率及节水潜力分析[J]．水科学进展，2010，21(6)：788-794． CUI Yuanlai，TAN Fang，ZHENG Chuanju．Analysis of irrigation efficiency and water saving potential at different scales[J]．Advances in Water Science，2010，21(6)：788-794．(in Chinese)

2 杨晓慧，黄修桥，陈震，等．基于DSSAT模拟的灌溉用水效率评价指标比较[J]．农业工程学报，2015,31(24):95-100． YANG Xiaohui，HUANG Xiuqiao，CHEN Zhen，et al．Evaluation index comparison of different irrigation water use efficiency based on DSSAT simulation[J]．Transactions of the CSAE，2015，31(24):95-100．(in Chinese)

3 贾宏伟，郑世宗．灌溉水利用效率的理论、方法与应用[M]．北京：中国水利水电出版社，2013：10-35．

4 李浩鑫，邵东国，尹希，等．基于主成分分析和Copula函数的灌溉用水效率评价方法[J]．农业工程学报，2015, 31(11)：96-102． LI Haoxin，SHAO Dongguo，YIN Xi，et al．Evaluation method for irrigation water use efficiency based on principle component analysis and Copula function[J]．Transactions of the CSAE，2015, 31(11)：96-102．(in Chinese)

5 屈忠义，杨晓，黄永江，等．基于Horton分形的河套灌区渠系水利用效率分析[J]．农业工程学报，2015, 31(13)：120-127． QU Zhongyi，YANG Xiao，HUANG Yongjiang，et al．Analysis of efficiency of water utilization in canal-system in Hetao irrigation district based on Horton fractal[J]．Transactions of the CSAE，2015, 31(13)：120-127．(in Chinese)

6 MOLDEN David J．Accounting for water use and productivity[C]．SWIM Paper，1997: 1-16．

7 YILMAZ B，YURDUSEV M A，HARMANCIOGLU N B．The assessment of irrigation efficiency in Buyuk Menderes basin[J]．Water Resources Management，2009，23(6)：1081-1095．

8 雷贵荣，胡震云，韩刚．基于SFA的农业用水技术效率和节水潜力研究[J]．水利经济，2010，28(1)：55-58． LEI Guirong，HU Zhenyun，HAN Gang．Agricultural water technology based on SFA efficiency and water saving potential research[J]．Journal of Economics of Water Resources，2010，28(1)：55-58．(in Chinese)

9 刘军，朱美玲．农业用水效率评价指标体系研究[J]．节水灌溉，2013(5)：61-63． LIU Jun，ZHU Meiling．Research on evaluation index system of agricultural water use efficiency[J]．Water Saving Irrigation，2013(5)：61-63．(in Chinese)

10 李绍飞，余萍，孙书洪．灌溉用水效率评价指标及模型构建与实例应用[J]．中国农业大学学报，2014，19(3)：188-195． LI Shaofei，YU Ping，SUN Shuhong．Evaluation index of irrigation water efficiency and case verification[J]．Journal of China Agricultural University，2014，19(3)：188-195．(in Chinese)

11 张义盼，崔远来，史伟达．农业灌溉节水潜力及回归水利用研究进展[J]．节水灌溉，2009(5)：50-54． ZHANG Yipan，CUI Yuanlai，SHI Weida．Advance in agriculture irrigation water-saving potential and reuse of return flow research[J]．Water Saving Irrigation，2009(5)：50-54．(in Chinese)

12 王锦辉，费良军，谢芳，等．灰色关联理论-TOPSIS 法的大型灌区运行状况综合评价[J]．排灌机械工程学报，2015,33(11):985-990． WANG Jinhui，FEI Liangjun，XIE Fang，et al．Comprehensive evaluation of operational status of large-scale irrigation district based on grey relation theory and TOPSIS method[J]．Journal of Drainage and Irrigation Machinery，2015,33(11):985-990． (in Chinese)

13 付强．数据处理方法及其农业应用[M]．北京：科学出版社，2006：10-45．

14 杨增玲，楚天舒，韩鲁佳，等．灰色关联理想解法在秸秆综合利用方案优选中的应用[J]．农业工程学报，2013，29(20)：179-191． YANG Zengling，CHU Tianshu，HAN Lujia，et al．Application of GC-TOPSIS on optimizing choice of utilization programs of crop straw[J]．Transactions of the CSAE，2013，29(20)：179-191．(in Chinese)

15 DAI J，JING Q I，CHI J，et al．Integrated water resource security evaluation of Beijing based on GRA and TOPSIS[J]．Frontiers of Earth Science in China，2010，4(3)：357-362．

16 刘渝．中西部地区农业水资源利用效率分析[D]．武汉：华中农业大学，2006．

17 彭致功，刘钰，许迪，等．灌溉用水管理评价指标体系构建及综合评价[J]．武汉大学学报：工学版，2009，42(5)：644-648． PENG Zhigong，LIU Yu，XU Di，et al．Construction of evaluation index system for irrigation water management and its comprehensive evaluation[J]．Engineering Journal of Wuhan University，2009，42(5)：644-648．(in Chinese)

18 李浩鑫，邵东国，何思聪，等．基于循环修正的灌溉用水效率综合评价方法[J]．农业工程学报，2014，30(5)：65-72． LI Haoxin，SHAO Dongguo，HE Sicong，et al．Comprehensive evaluation method for irrigation water use efficiency based on circulation-correction[J]．Transactions of the CSAE，2014，30(5)：65-72．(in Chinese)

19 郭亚军．综合评价理论、方法及应用[M]．北京：科学出版社，2007：15-29．

20 付强．水资源系统分析[M]．北京：中国水利水电出版社，2012：187-196．21 SAATY T L．Decision making with the analytic hierarchy process[J]．International Journal of Services Sciences，2008，1(1)：83-98．

22 NILSSON H，NORDSTRÖM E M，ÖHMAN K．Decision support for participatory forest planning using AHP and TOPSIS[J]．Forests，2016，7(5)： 7050100．

23 廖宇兰，刘世豪，孙佑攀，等．基于灵敏度分析的木薯收获机机架结构优化设计[J/OL]．农业机械学报，2013，44(12):56-61．http：∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20131210&journal_id=jcsam. DOI：10.6041/j.issn.1000-1298.2013.12.010. LIAO Yulan，LIU Shihao，SUN Youpan，et al．Structural optimization for rack of cassava harvester based on sensitivity analysis[J/OL]．Transactions of the Chinese Society for Agricultural Machinery，2013，44(12)：56-61．(in Chinese)

24 XU J，FENG P，YANG P．Research of development strategy on China’s rural drinking water supply based on SWOT-TOPSIS method combined with AHP-Entropy：a case in Hebei Province[J]．Environmental Earth Sciences，2016，75(1)：1-11．

25 费良军，王锦辉，王光社，等．基于改进熵权-G1-博弈论法的灌区运行状况综合评价[J]．排灌机械工程学报，2015，33(10)：895-900． FEI Liangjun，WANG Jinhui，WANG Guangshe，et al．Comprehensive evaluation of irrigation district operational status based on improved entropy weight-G1-game theory method[J]．Journal of Drainage and Irrigation Machinery，2015， 33(10)：895-900．(in Chinese)

26 陈加良．基于博弈论的组合赋权评价方法研究[J]．福建电脑，2003(9)：15-16． CHEN Jialiang．Study on comprehensive evaluation weighting method based on game theory[J]．Fujian Computer，2003(9)：15-16．(in Chinese)

27 苏观南，付修庆，刘天祥．改进的博弈论综合权重在大坝安全综合评价中的应用[J]．中国农村水利水电，2014(11)：82-85． SU Guannan，FU Xiuqing，LIU Tianxiang．Improved comprehensive weight calculated with game theory and its application in dam safety synthetic appraisal[J]．China Rural Water and Hydropower，2014(11)：82-85．(in Chinese)

28 李灿，张凤荣，朱泰峰，等．基于熵权TOPSIS模型的土地利用绩效评价及关联分析[J]．农业工程学报，2013，29(5)：217-227． LI Can，ZHANG Fengrong，ZHU Taifeng，et al．Evaluation and correlation analysis of land use performance based on entropy-weight TOPSIS method[J]．Transactions of the CSAE，2013，29(5)：217-227．(in Chinese)

29 刘震宇．灰色系统分析中存在的两个基本问题[J]．系统工程理论与实践，2000，20(9)：123-124． LIU Zhenyu．Two problems existing in gray systems analysis[J]．System Engineering—Theory and Practice，2000，20(9)：123-124．(in Chinese)

30 周翔，蒋根谋．基于组合赋权和改进灰色关联分析法的项目风险分析[J]．工程管理学报，2008(6)：78-81． ZHOU Xiang，JIANG Genmou．Risk analysis of construction project based on combination weighting and improved grey interrelated analysis method[J]．Journal of Engineering Management,2008(6)：78-81．(in Chinese)

31 姜秋香，付强，王子龙．基于粒子群优化投影寻踪模型的区域土地资源承载力综合评价[J]．农业工程学报，2011，27(11)：319-324． JIANG Qiuxiang，FU Qiang，WANG Zilong．Comprehensive evaluation of regional land resources carrying capacity based on projection pursuit model optimized by particle swarm optimization[J]．Transactions of the CSAE，2011，27(11)：319-324．(in Chinese)

32 邢贞相，闫丹丹，刘美鑫，等．三江平原近60年降水量时空变异特征分析[J/OL]．农业机械学报，2015，46(11)：337-344．http：∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20151146&journal_id=jcsam．DOI：10.6041/j.issn.1000-1298.2015.11.046. XING Zhenxiang，YAN Dandan，LIU Meixin，et al．Analysis of irrigation efficiency and water saving potential at different scales[J/OL]．Transactions of the Chinese Society for Agricultural Machinery，2015，46(11)：337-344．(in Chinese)

33 李晨洋．三江平原井渠结合灌区水资源可持续利用对策[J]．节水灌溉，2013(1)：41-43. LI Chenyang．Countermeasures for sustainable utilization of water resources in well & canal combination irrigation district of Sanjiang Plain[J]．Water Saving Irrigation，2013(1)：41-43．(in Chinese)

34 李晨洋，谢丹丹．三江平原引水灌区优化模型及应用[J]．中国农村水利水电，2013(4)：147-148． LI Chenyang，XIE Dandan．Sanjiang Plain water diversion irrigation optimization model and its application[J]．China Rural Water and Hydropower，2013(4)：147-148．(in Chinese)

35 蔡守华，张展羽，张德强．修正灌溉水利用效率指标体系的研究[J]．水利学报，2004,35(5)：111-115． CAI Shouhua，ZHANG Zhanyu，ZHANG Deqiang．Modified index system for utilization efficiency of irrigation water[J]．Journal of Hydraulic Engineering，2004,35(5)：111-115．(in Chinese)

36 LAI C，CHEN X，CHEN X，et al．A fuzzy comprehensive evaluation model for flood risk based on the combination weight of game theory[J]．Natural Hazards，2015，77(2)：1243-1259．

37 王鹏新，孙辉涛，王蕾，等．基于4D-VAR和条件植被温度指数的冬小麦单产估测[J/OL]．农业机械学报，2016, 47(3)：263-271．http：∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160337&journal_id=jcsam．DOI：10.6041/j.issn.1000-1298.2016.03.037. WANG Pengxin，SUN Huitao，WANG Lei，et al．Winter wheat yield estimation based on 4D variational assimilation method and remotely sensed vegetation temperature condition index[J/OL]．Transactions of the Chinese Society for Agricultural Machinery，2016, 47(3)：263-271．(in Chinese)

38 郭燕红，邵东国，刘玉龙，等．工程建设效果后评价博弈论集对分析模型的建立与应用[J]．农业工程学报，2015， 31(9)：5-12． GUO Yanhong，SHAO Dongguo，LIU Yulong，et al．Establishment and application of set pair analysis model based on game theory for post-assessment of project construction effectiveness[J]．Transactions of the CSAE，2015，31(9)：5-12．(in Chinese)

39 周和平，张明义，周琪，等．新疆地区农业灌溉水利用系数分析[J]．农业工程学报，2013，29(22)：100-107． ZHOU Heping，ZHANG Mingyi，ZHOU Qi，et al．Analysis of agricultural irrigation water-using coefficient in Xinjiang arid region[J]．Transactions of the CSAE，2013，29(22)：100-107．(in Chinese)

Evaluation Model of Irrigation Water Use Efficiency Based on Game Theory and GRA-TOPSIS

LIU Dong1,2GONG Fanghua1FU Qiang1FAIZ M Abrar1LI Tianxiao1CUI Song1
(1.SchoolofWaterConservancyandCivilEngineering，NortheastAgriculturalUniversity，Harbin150030，China2.KeyLaboratoryofEffectiveUtilizationofAgriculturalWaterResources，MinistryofAgriculture，Harbin150030，China)

An objective and comprehensive indicator system was established to evaluate the irrigation water use efficiency of irrigation districts. The subjective weights estimated by analytic hierarchy process (AHP) and the objective weights figured out by improved entropy value method (IEVM) were integrated through using the idea of game theory (GT) to gain a set of final indicator weights．The gray relation analysis (GRA) and technique for order preference by similarity to ideal solution (TOPSIS) model were combined to assess regional irrigation water use efficiency with combinational weights．Totally ten large-scale irrigation districts in Sanjiang Plain were chosen as the case study to validate this model and index system, and the evaluation results of the proposed GRA-TOPSIS method were compared with those of GRA and TOPSIS. The water use efficiencies of these irrigation districts were evaluated and ranked by the three methods， respectively．The results showed that the Spearman’s rank coefficients between the results of GRA-TOPSIS and those of GRA and TOPSIS were 0.952 and 0.927， respectively， which illustrated that the results of GRA-TOPSIS were consistent with those of GRA or TOPSIS．The correlation coefficients between the effective irrigation water utilization coefficient and the results based on the GRA-TOPSIS method， GRA and TOPSIS were 0.863， 0.742 and 0.736， respectively， implying that the GRA-TOPSIS was superior to GRA and TOPSIS．In addition， the range of comprehensive value obtained by GRA-TOPSIS model was 0.343 with variation coefficient of 0.267， which were all above the ranges and variation coefficients of GRA or TOPSIS methods， revealing a higher resolution ratio and evenness of GRA-TOPSIS model over those of the other two models．Therefore， the GRA-TOPSIS can efficiently assess the irrigation water use efficiency and lead to great convenience to the practice of water resources management．Meanwhile, the indexes of the criterion layer constituted by water-use index, engineering conditions and management level, were evaluated with GRA-TOPSIS．According to the degrees of variation between the ranks of criterion layer and the ranks of target layer, these irrigation districts can be divided into three categories so as to find out the main factors affecting each irrigation district．Wutonghe, Xingkaihu and Jiangchuan irrigation districts were in Ⅰ category, which should make all-round effort to build up the irrigation districts. Yintang, Yuelai, Jidong, Xingfu and Hamatong irrigation districts were in Ⅱ category, which should take advantage of the ranks of indicator layer to make further development strategy．Wokenhe and Longtouqiao irrigation districts were in Ⅲ category, which should make a great improvement in one aspect of criterion layer．In conclusion, the research provided references for evaluating regional irrigation water use efficiency and formulating development strategy for irrigation districts．

irrigation water use efficiency；large-scale irrigation district；game theory；gray relation analysis；technique for order preference by similarity to ideal solution；comprehensive evaluation

2016-09-20

2016-10-21

国家自然科学基金项目(51579044、41071053、51479032)、哈尔滨市创新人才研究专项资金(优秀学科带头人)项目 (2013RFXXJ001)和黑龙江省水利科技项目(201319、201501、201503)

刘东(1972—)，男，教授，博士生导师，主要从事水土资源优化利用与管理研究，E-mail: liudong@neau.edu.cn

付强(1973—)，男，教授，博士生导师，主要从事农业水土资源分析和冻融土壤水热作用机理研究，E-mail: fuqiang0629@126.com

10.6041/j.issn.1000-1298.2017.05.027

S274.4

A

1000-1298(2017)05-0218-09