考虑不同层次利益主体的灌溉水资源优化配置
2017-06-05李茉姜瑶,2郭萍,2李江
李 茉 姜 瑶,2 郭 萍,2 李 江
(1.中国农业大学中国农业水问题研究中心, 北京 100083; 2.中国农业大学中国-以色列国际农业研究培训中心, 北京 100083)
考虑不同层次利益主体的灌溉水资源优化配置
李 茉1姜 瑶1,2郭 萍1,2李 江1
(1.中国农业大学中国农业水问题研究中心, 北京 100083; 2.中国农业大学中国-以色列国际农业研究培训中心, 北京 100083)
针对灌溉水资源优化配置中存在的非线性和不确定性等特点,同时考虑灌区不同层次决策主体利益,分别构建考虑上层管理者利益的区间线性分式规划(ILFP)模型以获得最大的灌溉水生产力和考虑下层农民利益的区间二次规划(IQP)模型以获得最大的产量。在此基础上,将灌区上、下层利益主体作为整体,构建线性分式二次双层规划(LFQBP)模型,以协调灌区不同层次决策主体利益,促进灌区可持续发展。将所构建模型应用于盈科灌区的粮食作物配水中。通过配水结果的比较来分析各模型的性质,结果表明ILFP模型和LFQBP模型更适用于干旱地区。所构建模型从不同角度反映灌溉配水的实际问题,其优化结果有助于灌区管理者权衡各层决策主体间的利益。
灌溉水资源; 优化配置; 利益主体; 线性分式二次双层规划; 不确定性
引言
农业是我国用水大户,农业用水占全国总用水量的63.5%,其中,灌溉总用水量占农业总用水量的90%以上[1]。我国灌溉水资源短缺,用水效率低,在西北旱区尤为突出。灌溉用水是灌区水资源消耗的主要途径和保证粮食安全生产的重要手段[2],如何科学地优化且合理地配置有限的灌溉水资源对提高灌区水资源利用效率和保障粮食安全具有十分重要的意义。
灌溉水资源优化配置中,存在不同层次的利益主体。以灌区为单位,处于灌区上层的决策主体(管理者),通常倾向于在获得灌区最大产量或效益的同时尽可能节约灌溉水资源量,即获得最大的灌溉水生产力,以实现灌区可持续发展。而处于灌区下层的决策主体(农民),希望获得最大的产量或效益,以提高自身生活水平。不同层次决策主体侧重的目标不同,获得的配水方案也不同,灌区水资源管理决策者应了解各层次的配水倾向并做调整,以单一层次目标决策出的配水方案来指导整个灌区的灌溉用水将不能最大限度地满足灌区整体的利益需求。
国内外近年来基于主体的水资源配置从3方面进行考虑:①考虑多目标的水资源配置以体现各决策主体之间的互动[3-5]。②通过大系统理论来协调不同层次利益主体的决策[6-7]。③基于博弈论的水资源配置分析用水主体行为间相互制约、相互作用的规律[8-9]。上述各项研究从不同角度进行了基于主体的水资源配置研究,其中前2方面以优化目标的角度描述配置问题,通过优化方法来协调各决策主体的利益,而第3方面主要讨论主从关系和合作关系的水资源用户博弈模型,强调个体决策最优。上述各成果集中于流域尺度和区域尺度的研究,缺乏灌区尺度的相关研究。另外,从优化角度出发基于利益主体的水资源配置模型多为普通线性规划,然而灌溉水资源优化配置具有变量多、结构复杂、非线性等特点[10],普通线性规划模型已不能充分刻画上述各层次目标函数,加之配水过程中存在的不确定性[11-13],致使灌溉水资源优化配置困难。同时,由于不同层次利益主体间存在矛盾与竞争,如何在一个大系统内协调上、下两层决策主体的利益,注重不同层次决策主体用水行为的互动,使得配水方案尽可能让双方决策者满意是保证灌区经济发展和社会稳定需要考虑的问题。
本文首先分别构建不确定条件下考虑不同层次利益主体的灌溉优化配水模型;其次,根据不同层次利益主体需求,为实现灌区可持续发展,尝试构建协调上、下两层决策主体利益的灌溉水资源优化配置模型,并给出上述各模型的求解方法。将所构建的模型应用于黑河中游盈科灌区粮食作物的配水中,通过模型优化结果的比较来展示所构建模型的性质与适用性,为灌溉水资源优化配置提供方法。
1 模型建立
包括3部分:①构建不确定性条件下分别考虑灌区上、下两层利益主体的灌溉水资源优化配置模型,即区间线性分式规划(ILFP)配水模型(上层)和区间二次规划(IQP)配水模型(下层)。②构建协调上、下两层利益主体的线性分式二次双层规划(LFQBP)配水模型。③各模型解法。所构建的模型均为一般形式,其决策变量为灌区不同作物的灌溉水量,目标函数随各层利益主体的不同而不同。
1.1 IQP模型和ILFP模型构建
考虑下层农民利益,以作物总产量最大为目标函数,其中作物产量又与作物用水量相关,用作物全生育期的水分生产函数来表示。典型的全生育期水分生产函数有线性模型和二次函数模型,大量研究表明,线性关系一般只适用于灌溉水源不足、管理水平不高、农业技术措施未能充分发挥的中低产地区,随着水源条件的改善和管理水平的提高,作物全生育期水分生产函数呈二次抛物线关系[14]。采用二次规划来描述农民层次产量与水量之间的关系,模型目标函数为
(1)
式中Z1——作物产量j——作物种类序号xj——第j种作物的灌溉水量aj、bj、γj——第j种作物水分生产函数的二次项、一次项和常数项系数
考虑上层管理者利益,以灌溉水分生产力最大为目标函数,即达到单位用水下的产量最大,该目标可表示成线性分式规划问题[13]。模型目标函数为
(2)
式中Z2——作物水分生产力cj、α——与产量或产值相关的参数dj、β——与水量相关的参数
上述两模型的约束条件可概化为
(3)
xj≥0 (j=1,2,…,J)
(4)
式中mij——决策变量前系数ni——约束右端项
具体到灌溉水资源优化配置,约束条件应包括不同水源的供水量约束、不同作物的需水量约束、水转换约束、政策性约束等。
考虑到灌溉水资源优化配置过程中存在的诸多不确定性,例如由气候变化和人类活动引起的水文要素呈现的随机性;社会经济管理及相关政策中涉及到的灰色性和模糊性等,本文将不确定性技术引入上述两模型中。随机规划、模糊规划和区间规划是3种常见的不确定性规划方法。其中随机规划和模糊规划的求解分别建立在参数的概率分布和隶属度函数分布的基础上,获得这些分布需要大量的数据。相比之下,区间规划只需知道模型系统中不确定性参数的波动区间(参数的上、下限值)而无需知道具体的随机分布或模糊隶属度函数,所需数据量大大减少。对于农业灌溉水量配置而言,一些参数需要实验数据做支撑,例如作物水分生产函数,该类数据通常系列较短,拟合其随机分布或隶属度函数较困难,还有一些参数本身随时间序列变化不大,没有明显的随机特征,例如作物种植面积。因此,区间规划可以用来反映农业灌溉水资源配置中的不确定性。另外,由HUANG等[15]开发的两步交互式算法也已极大地简化了区间规划的计算过程。综上,由较易获取的不确定性参数、简洁的表达形式和便捷的求解方法,本文将区间规划引入农业灌溉优化配水模型中以增加模型的实用性,分别形成以考虑下层农民利益的IQP配水模型和考虑上层管理者利益的ILFP配水模型:
IQP模型
(5)
ILFP模型
(6)
约束条件
(7)
(8)
一般令x±=[x-,x+]表示区间数,其中,x-、x+分别表示区间数x±的下限值和上限值。
1.2 LFQBP模型构建
为缓解系统内不同层次利益主体间的矛盾,需要将系统内各层次目标作为一个分层次的整体,优化出一组能够尽量满足上、下两层利益的配水方案,即LFQBP配水模型。LFQBP模型的上层目标函数为灌区水分生产力最大(管理者利益),下层目标函数为作物产量最大(农户利益)。LFQBP模型的特点是在一个决策系统内,以管理者利益为主要利益,同时协调下层农民利益,达到各层利益之间的妥协。LFQBP模型可表述成上层目标(式(2))和下层目标(式(1))。LFQBP模型的约束条件同式(3)和式(4)。
1.3 模型求解
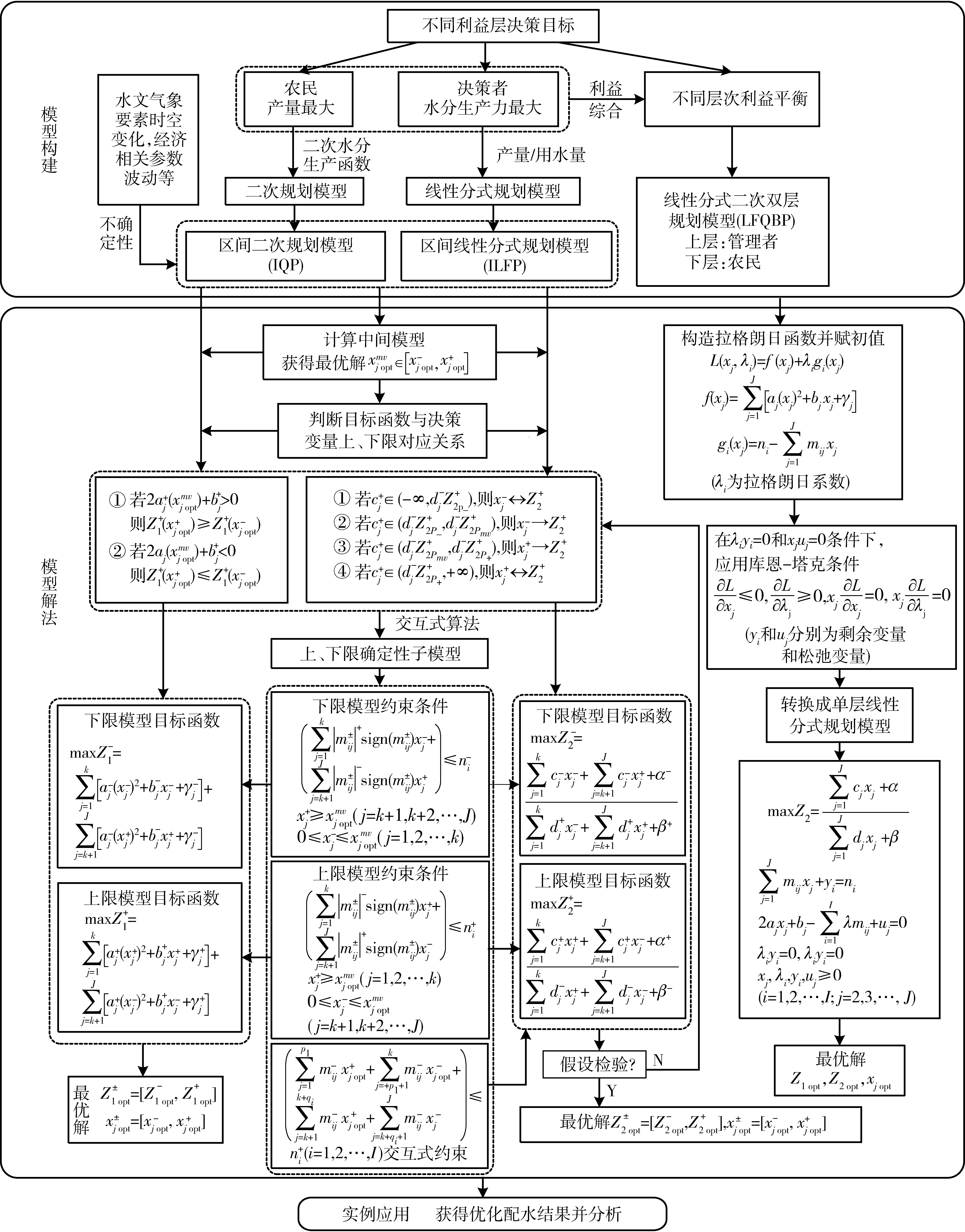
图1 模型构建及解法Fig.1 Model building and solution
2 实例研究
2.1 研究区域概况
盈科灌区位于黑河流域中游张掖市(100°17′~100°34′E、38°50′~38°58′N),属内陆干旱气候。年均降水量为125 mm,年均蒸发量为1 200 mm,蒸发量远大于降水量,水资源短缺严重。灌区主要农作物包括玉米(大田玉米和制种玉米)、小麦、瓜菜等,其中小麦和玉米的种植面积占所有作物种植面积的83%,经济作物面积占15%[19]。根据研究区域实际情况,考虑盈科灌区不同层次决策主体的利益,对灌区粮食作物进行不同月份的地表水和地下水联合配置决策。
2.2 作物配水优化模型
(1)目标函数
从灌区农民利益出发,以粮食作物总产量最高为目标函数
(9)
式中Y——粮食作物总产量,102kgi——作物种类,i=1代表大田玉米,i=2代表制种玉米,i=3代表小麦
t——作物生育期内各月份,t=1~6,分别代表4—9月份
Ai——第i种作物的种植面积,102hm2
Sit、Git——第i种作物第t月份的地表水、地下水配水量,cm
ai、bi、γi——第i种作物水分生产函数的二次项、一次项、常数项系数
从灌区管理者利益出发,以作物整体水分生产力最大为目标函数
(10)
式中WP——作物水分生产力,kg/m3Pi——第i种作物的单方水产量,kg/m3
综合灌区管理者和农民之间的利益关系,构建协调管理者和农民利益的LFQBP模型,其中上层规划目标函数为式(10),下层规划目标函数为式(9)。
(2)约束条件
地表水可供水量约束
(11)
式中Wt——第t月份的地表水可供水量,104m3
β1、β2——渠系水利用系数、田间灌溉水利用系数
地表水、地下水转换约束
(12)
式中θ1、θ2、θ3——渠系渗漏损失系数、田间水入渗系数、降水入渗补给系数
Δht——第t月份的地下水位差,cm
μ——地下含水层给水度
Rt——第t月份的有效降水量,cm
需水量约束
Sit+Git+Rt≥Iit(i=1,2,3;t=1,2,…,6)
(13)
式中Iit——第i种作物第t月份的灌溉需水量,cm
非负约束
Sit≥0Git≥0 (i=1,2,3;t=1,2,…,6)
(14)
2.3 模型参数确定
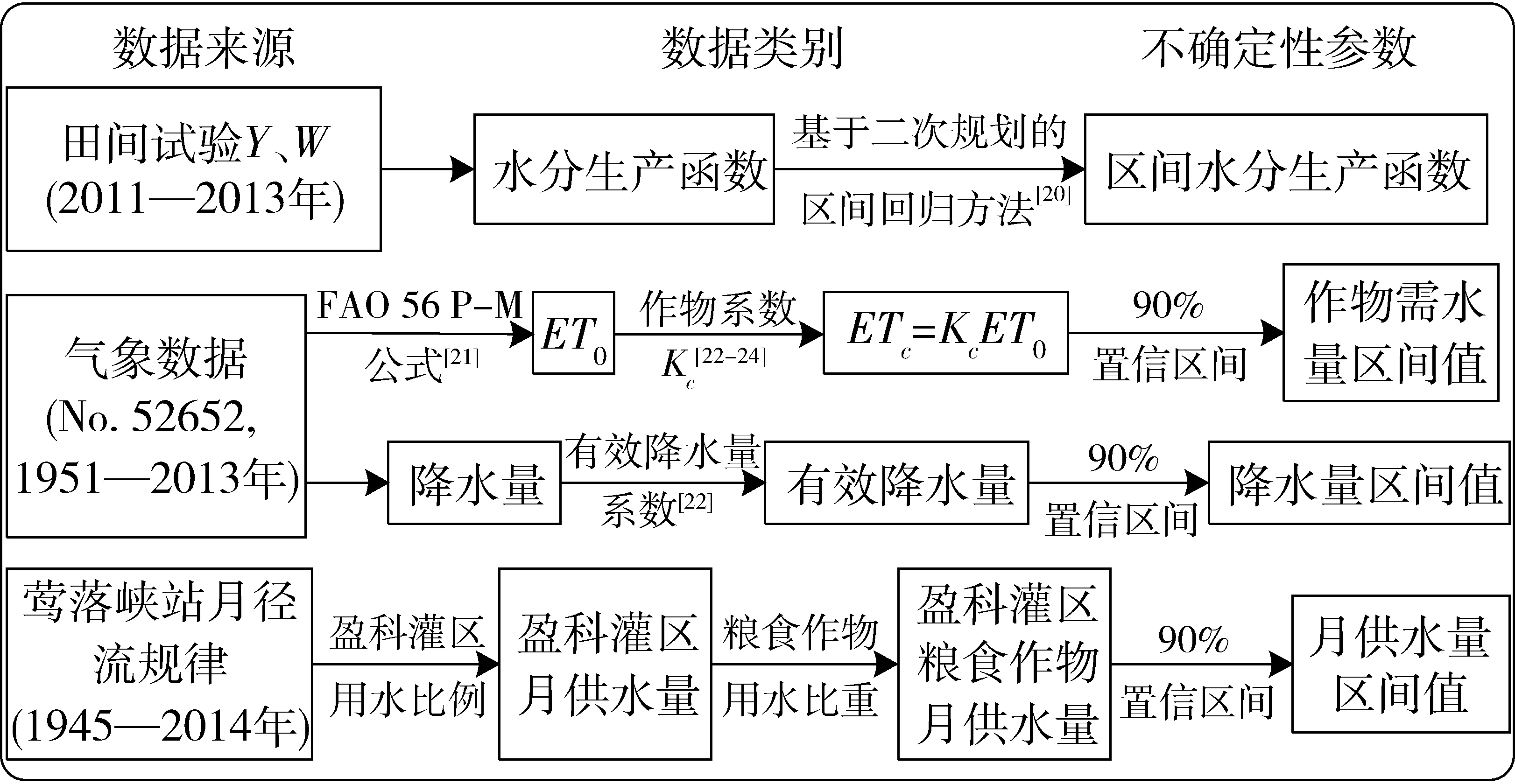
图2 参数获得与处理Fig.2 Parameter acquisition and processing
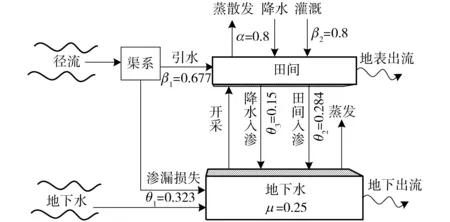
图3 地表水、地下水转换关系及对应系数确定Fig.3 Surface water and groundwater transformation and their corresponding coefficients determination
作物水分生产函数、需水量、降水量、可供水量数据的获得与处理见图2。根据实际情况,春小麦的生育阶段为4月1日—7月20日,玉米的生育阶段为4月20日—9月22日。不同作物单方水产量区间值由拟合的区间作物水分生产函数与对应的需水量区间值(减去降水量)相除获得。地表水量与地下水量之间的转换关系及相关系数见图3。图3中各系数的获得参照项国圣[25]的研究成果,实线表示模型参数,虚线表示模型变量。其余参数包括作物种植面积、地下水位等数据均来自调研统计资料。其中各月份地下水位差计算采用盈科灌区包括盈科干渠、南关、下秦等12个观测井从1985—2010年地下水位观测数据的平均值计算。模型基础参数区间值见表1~3,地表供水量、有效降水量、需水量均值见图4。
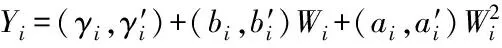

表2 地表可供水量与有效降水量Tab.2 Surface water supply and effective rainfall

表3 作物蒸散发量Tab.3 Crop evapotranspiration mm
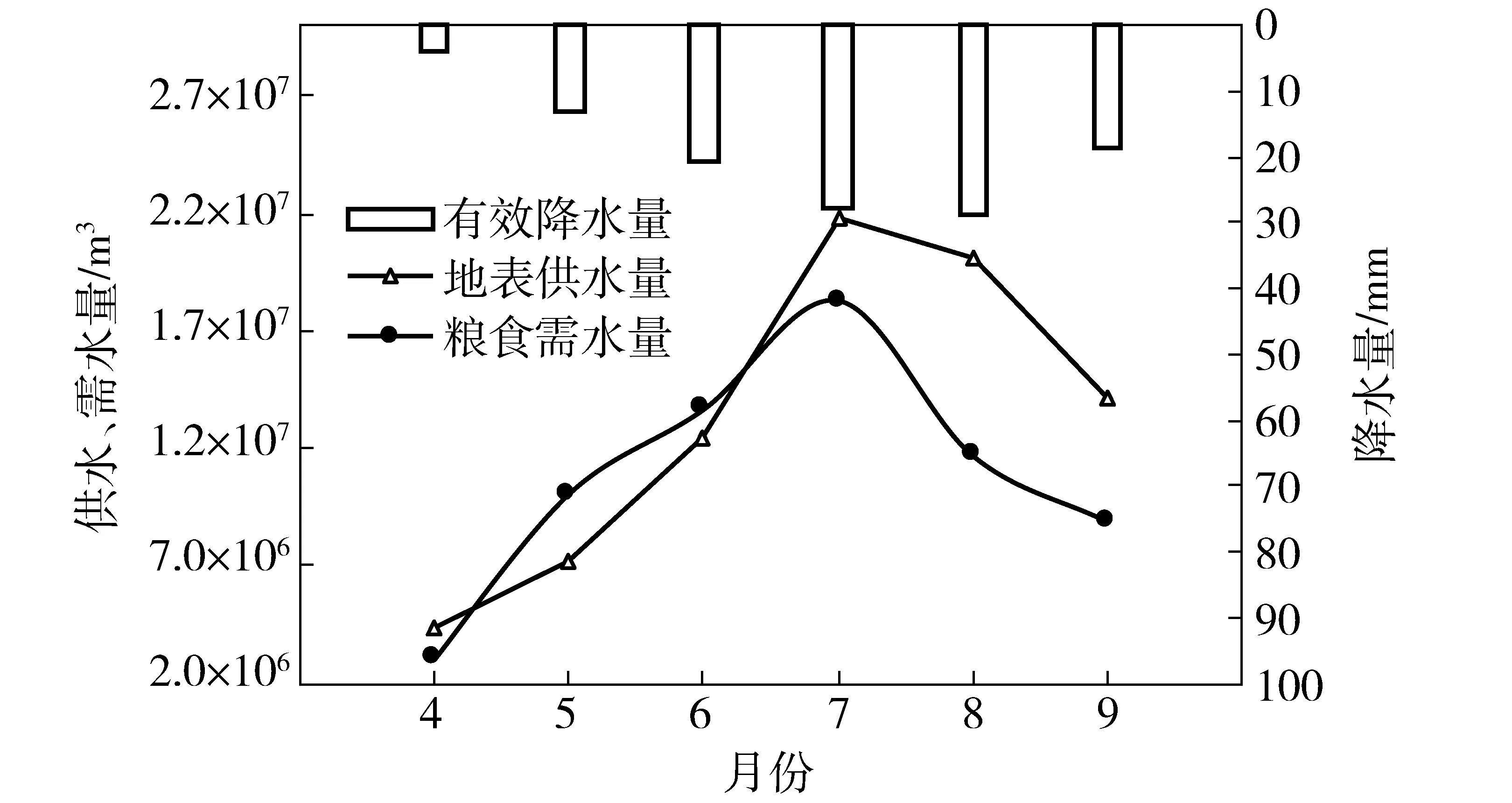
图4 供、需水量均值Fig.4 Average water supply and demand amounts
3 结果与分析
按照前述模型解法,考虑灌区不同层次利益主体及配水过程中存在的不确定性,分别求解IQP和IFLP模型,得到盈科灌区不同作物不同月份的地表水和地下水配水方案。图5、图6分别为IQP模型和IFLP模型3种粮食作物在生育阶段内各月份的总配水量情况。2个模型的结果均用区间数表示,说明优化配水结果对模型输入的不确定性是敏感的。IQP模型和IFLP模型关于3种粮食作物在不同月份内的配水规律是一致的。对于IQP模型的单位面积总配水量由大到小为:大田玉米([75.64 cm, 89.15 cm])、制种玉米([70.82 cm, 75.33 cm])、小麦([53.37 cm, 55.31 cm]);同样,对于IFLP模型的单位面积总配水量由大到小为:大田玉米([75.64 cm, 85.15 cm])、制种玉米([58.13 cm, 63.17 cm])、小麦([44.92 cm, 48.31 cm])。大田玉米单位面积总配水量最多,是因为大田玉米的单方水产量是3种作物中最高的,这由作物水分生产函数决定。即在给予同样水量的前提下,大田玉米获得的产量最高,其次是制种玉米,最后是小麦。对于每种作物不同月份内的配水量,无论是IQP模型还是IFLP模型,配水量都呈现先增加后递减的趋势。大田玉米的配水集中在7—9月份,制种玉米的配水集中在6—8月份,小麦的配水集中在5—7月份,配水规律与需水规律一致。IQP模型各月份配水量均值占总配水量比例为:6.56%(4月份)、15.67%(5月份)、21.18%(6月份)、26.60%(7月份)、17.04%(8月份)、12.95%(9月份);IFLP模型各月份配水量均值占总配水量比例为:6.09%(4月份)、15.62%(5月份)、21.30%(6月份)、27.79%(7月份)、17.72%(8月份)、11.49%(9月份)。基于区间数的决策方案能够给决策者提供更多的配水方案参考,激进的决策者倾向于选取配水量上限值,以便获得较高的产量或水分生产力,同时,由于可供水量是有限的,在规划年不易确定来水量是否能够达到上限值,因此该种决策存在一定的缺水风险。反之,保守的决策者倾向于选取配水量下限值,以便尽可能保证所有作物用水需求,但同时,获得的产量或水分生产力相对较低。
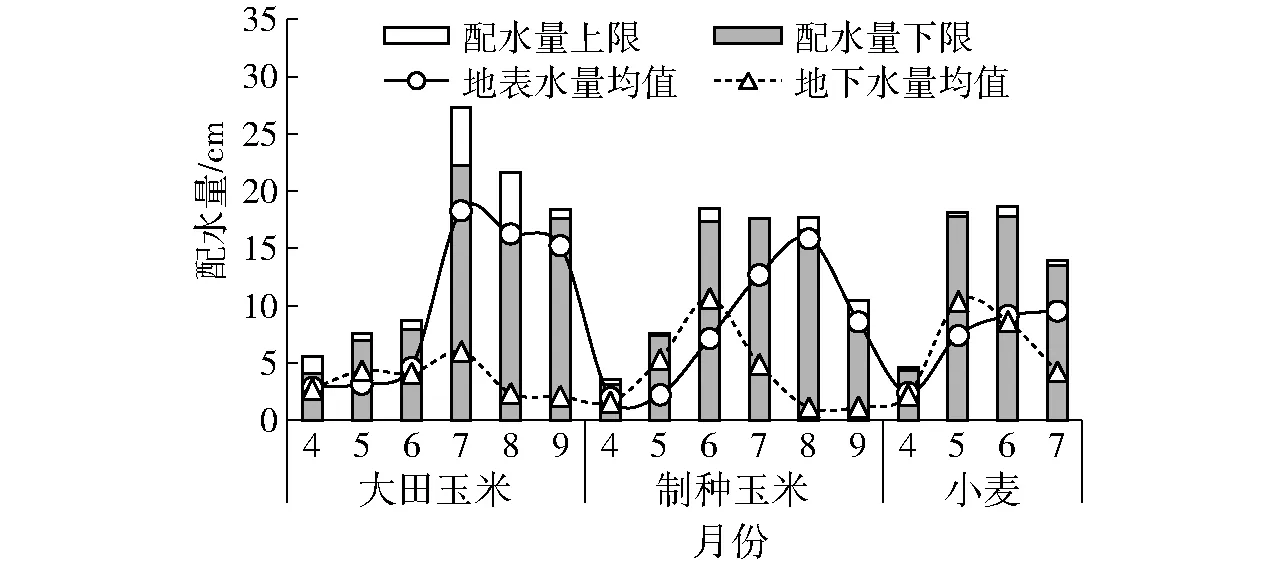
图5 IQP模型配水结果Fig.5 Solution of IQP model
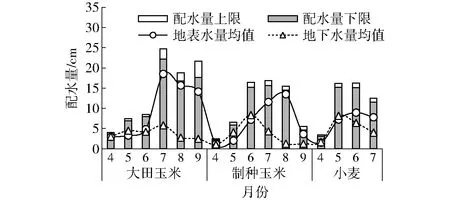
图6 ILFP模型配水结果Fig.6 Solution of ILFP model
根据图5和图6所示的各作物单位面积优化配水量,同时考虑各作物的灌溉面积,可知IQP模型的总配水量比IFLP模型多[768.94万m3, 790.29万m3],这是由于2个模型考虑的利益主体不同。IQP模型考虑的是农民的利益,希望获得最大的产量,即在有限的可供水量和不超过每种作物最大产量对应的灌水量的前提下,分配给作物的水量越多对提高产量越有利;而IFLP模型考虑的是决策者的利益,即获得最大的作物水分生产力。IFLP模型的水分生产力(总产量与总用水量之比)为[1.54 kg/m3, 1.56 kg/m3],IQP模型的水分生产力为[1.37 kg/m3, 1.39 kg/m3],IFLP模型的水分生产力比IQP模型高0.17 kg/m3,从结果中可以看出,在保证每种作物需水量要求的情况下,IFLP模型趋向于分配给作物较少的水量来获得较高的水分生产力。
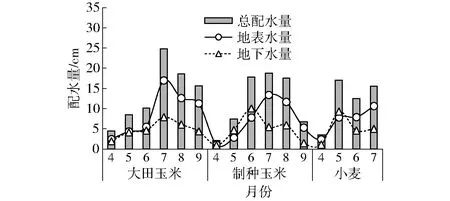
图7 LFQBP模型配水结果Fig.7 Solution of LFQBP model
LFQBP模型的优点是能够平衡上层和下层决策主体的利益,优化出一组能够最大限度同时满足上、下层决策者利益的配水方案。图7为LFQBP模型优化出的3种粮食作物不同月份的地表水和地下水的配水方案。从图中可以看出,LFQBP模型的配水规律与IFLP模型和IQP模型的配水规律类似,即各月份的配水集中在6—8月份;大田玉米被分配的单位面积水量最多,其次是制种玉米,最后是小麦;3种作物地表水配水量均大于地下水配水量。表4给出了不同模型对3种作物优化得到的全生育期累计配水量均值。从表中可以看出,3种模型中大田玉米的总配水量相同,原因与上述相同,即由于大田玉米单方水产量最高,水量优先分配给大田玉米。由于制种玉米在3种粮食作物中占有最大的灌溉面积,因此制种玉米的总配水量最多。3种模型各月份的单位面积配水量存在差异,见图5~7。对于制种玉米和小麦,IQP模型总配水量最多,IFLP模型总配水量最少,LFQBP模型的总配水量在IQP模型和IFLP模型之间,3种模型对各作物配水量趋势与总配水量趋势基本一致。表5对IQP模型、ILFP模型和LFQBP模型的总配水量、产量和水分生产力的均值进行比较。从表中可以看出,若单纯注重灌区上层管理者的利益,则总配水量为5 501万m3,水分生产力为1.55 kg/m3,虽然该结果比单纯注重农民利益的配水结果节水800万m3,且水分生产力增加0.17 kg/m3,但粮食产量降低15 900 kg,直接造成农民的经济损失,从而可能影响农民种植积极性。而LFQBP模型的优点即能够在一个系统内寻找灌区上层管理者利益和灌区下层农民利益之间的平衡点,LFQBP模型以灌区上层管理利益为主要利益,但同时又能尽量满足灌区下层农民的利益。LFQBP模型的计算结果显示,总配水量为6 034万m3,比单纯考虑灌区上层管理者利益(ILFP模型)的结果多配水533万m3,比单纯考虑灌区下层农民利益(IQP模型)的结果节水267万m3,就总配水量而言,若以ILFP模型配水量结果为起点,IQP模型配水量结果为终点,整个配水量长度设为1,则LFQBP模型的结果在距离起点0.67处寻优到了配水量的平衡点,即可以理解成LFQBP模型的配水量结果中,67%倾向于上层管理者利益,33%倾向于下层农民利益。同理,就产量而言,LFQBP模型的结果中76%倾向于上层管理利益,24%倾向于下层农民利益;就水分生产力而言,LFQBP模型的结果中65%倾向于上层管理者利益,35%倾向于下层农民利益。综上,IQP模型的配水量最多,产量最大,但水分生产力最低;ILFP模型的配水量最少,产量最低,但水分生产力最高;LFQBP模型中这3个指标值均在IQP模型和ILFP模型之间,平衡了灌区上、下两层的利益,在有限的可供水量下,LFQBP模型能够保证灌区作物产量和水分生产力均达到较高水平,有利于灌区的社会经济稳定,促进灌区可持续发展。

表4 不同模型不同作物全生育期累计配水量均值Tab.4 Total average water allocation amount of different crops and models 万m3
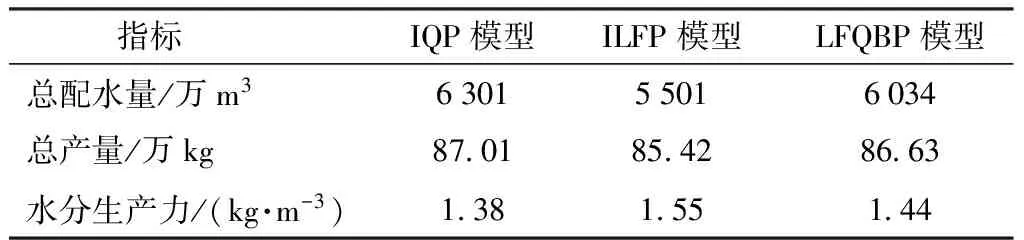
表5 IQP模型、ILFP模型、LFQBP模型比较Tab.5 Comparison of IQP model, ILFP model and LFQBP model
4 结论
(1)针对灌区配水不同层次利益主体,同时考虑配水过程中涉及到的不确定性,分别构建以下层农民期望的产量最大为目标的区间二次规划(IQP)模型和以上层管理者期望的灌溉水生产力最大为目标的区间线性分式规划(ILFP)模型。在此基础上,构建了线性分式二次双层规划(LFQBP)配水模型,该模型将灌区不同层次决策作为一个整体,能够有效协调上、下两层利益间矛盾,通过调节上、下层配水方案达到灌区产量和水分生产力均较高的水平,可促进灌区可持续发展。
(2)给出IQP模型、ILFP模型和LFQBP模型的表达形式及求解方法,其中IQP模型和ILFP模型求解的核心为将不确定性模型转换成确定性的子模型进行求解,而LFQBP模型求解的核心为将双层规划模型转变成单层规划模型进行求解。将所构建的3个模型应用于黑河中游盈科灌区粮食作物的配水中,IQP模型、ILFP模型和LFQBP模型的平均总配水量分别为6 301万m3、5 501万m3、6 034万m3,LFQBP较IQP模型产量虽然减少0.44%,水分生产力却提高4%,LFQBP模型较ILFP模型水分生产力降低7.64%,产量仅提高1.42%。可以看出,3种粮食作物在配水量达到一定程度后,产量变化微小,从灌区可持续发展角度来讲,ILFP模型和LFQBP模型更适用于干旱半干旱地区。
(3)IQP模型和ILFP模型考虑到了配水过程中存在的水文及管理不确定性,但IQP模型和ILFP模型仅能优化单一层次利益主体的目标。LFQBP模型虽然能够综合不同层次之间的利益关系,由于模型解法限制,没有将配水过程中存在的不确定性反映在模型中,这将是对LFQBP模型改进的一个重要方向。
1 冯保清. 我国不同尺度灌溉用水效率评价与管理研究[D]. 北京:中国水利水电科学研究院, 2013. FENG Baoqing. Study on the evaluation and management of irrigation water use efficiency for different scales in countrywide [D]. Beijing: China Institute of Water Resources & Hydropower Research, 2013. (in Chinese)
2 张智韬, 粟晓玲, 党永仁, 等. 泾惠渠灌区作物种植结构变化对灌溉需水量的影响[J/OL]. 农业机械学报, 2016, 47(10): 122-130.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20161017&flag=1&journal_id=jcsam. DOI: 10.6041/j.issn.1000-1298.2016.10.017. ZHANG Zhitao, SU Xiaoling, DANG Yongren, et al. Influence of crop planting structure change on irrigation water requirement in Jinghuqu Irrigation Area [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(10): 122-130. (in Chinese)
3 ROOZBAHANI R, ABBASI B, SCHREIDER S, et al. A multi-objective approach for transboundary river water allocation [J]. Water Resources Management, 2014, 28: 5447-5463.
4 DAVIJANI M H, BANIHABIB M F, ANVAR A N, et al. Multi-objective optimization model for the allocation of water resources in arid regions based on the maximization of socioeconomic efficiency [J]. Water Resources Management, 2016, 30: 927-946.
5 张智韬, 刘俊民, 陈俊英, 等. 基于RS、GIS和蚁群算法的多目标渠系配水优化[J]. 农业机械学报, 2010, 41(11): 72-78. ZHANG Zhitao, LIU Junmin, CHEN Junying, et al. Water resources allocation of canal system based on multi-objective about RS, GIS and ant colony algorithm [J]. Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(11): 72-78. (in Chinese)
6 陈晓宏, 陈永勤, 赖国友. 东江流域水资源优化配置研究[J]. 自然资源学报, 2002, 17(3): 366-372. CHEN Xiaohong, CHEN Yongqin, LAI Guoyou. Optimal allocation of water resources in Dongjiang River Basin [J]. Journal of Natural Resources, 2002, 17(3): 366-372. (in Chinese)
7 吴丹, 吴凤平, 陈艳萍. 流域初始水权配置复合系统双层优化模型[J]. 系统工程理论与实践, 2012, 32(1): 196-202. WU Dan, WU Fengping, CHEN Yanping. The bi-level optimization model of the compound system for basin initial water right allocation [J]. Systems Engineering-Theory & Practice, 2012, 32(1): 196-202. (in Chinese)
8 MADANI K. Game theory and water resources [J]. Journal of Hydrology, 2010, 381(3-4): 225-238.
9 付湘, 陆帆, 胡铁松. 利益相关者的水资源配置博弈[J]. 水利学报, 2016, 47(1): 38-43. FU Xiang, LU Fan, HU Tiesong. Game theory in water resources allocation for stakeholders [J]. Journal of Hydraulic Engineering, 2016, 47(1): 38-43. (in Chinese)
10 张展羽, 司涵, 冯宝平, 等. 缺水灌区农业水土资源优化配置模型[J]. 水利学报, 2014, 45(4): 403-409. ZHANG Zhanyu, SI Han, FENG Baoping, et al. An optimal model for agriculture water and soil resources configuration in water shortage irrigation area [J]. Journal of Hydraulic Engineering, 2014, 45(4): 403-409. (in Chinese)
11 付强, 刘银凤, 刘东, 等. 基于区间多阶段随机规划模型的灌区多水源优化配置[J]. 农业工程学报, 2016, 32(1): 132-139. FU Qiang, LIU Yinfeng, LIU Dong, et al. Optimal allocation of multi-water resources in irrigation area based on interval-parameter multi-stage stochastic programming model [J]. Transactions of the CSAE, 2016, 32(1): 132-139. (in Chinese)
12 莫淑红, 段海妮, 沈冰, 等. 考虑不确定性的区间多阶段随机规划模型研究[J]. 水利学报, 2014, 45(12): 1427-1434. MO Shuhong, DUAN Haini, SHEN Bing, et al. Study on an interval multi-stage stochastic programming approach [J]. Journal of Hydraulic Engineering, 2014, 45(12): 1427-1434. (in Chinese)
13 LI M, GUO P, SINGH V P. An efficient irrigation water allocation model under uncertainty [J]. Agricultural Systems, 2016, 144: 46-57.
14 康绍忠, 粟晓玲, 杜太生, 等. 西北旱区流域尺度水资源转化规律及其节水调控模式:以甘肃石羊河流域为例[M]. 北京:水利水电出版社,2009.
15 HUANG G H, BAETA B W, PATRY G G. A grey linear programming approach for municipal solid waste management planning under uncertainty [J]. Civil Engineering Systems, 1992, 9(4): 319-335.
16 CHEN M J, HUANG G H. A derivative algorithm for inexact quadratic program-application to environmental decision-making under uncertainty [J]. European Journal of Operational Research, 2001, 128(3): 570-586.
17 ARORA R, ARORA S R. An algorithm for solving an integer linear fractional/quadratic bilevel programming problem [J]. Advanced Modeling and Optimization, 2012, 14(1): 57-78.
18 ZHU H. Inexact fractional optimization for multicriteria resources and environmental management under uncertainty [D]. Regina: University of Regina, 2014.
19 JIANG Y, XU X, HUANG Q Z, et al. Assessment of irrigation performance and productivity in irrigated areas of the middle Heihe River basin using a distributed agro-hydrological model [J]. Agricultural Water Management, 2015, 147(1): 67-81.
20 TANAKA H, LEE H. Interval regression analysis by quadratic programming approach [J]. IEEE Transactions on Fuzzy Systems, 1998, 6(4): 473-481.
21 ALLEN R G, PEREIRA L S, RAES D, et al. Crop evapotranspiration—guidelines for computing crop water requirements. FAO Irrigation and Drainage Paper No.56[R]. Rome: FAO, 1998.
22 顾贺. 甘肃农业灌溉用水有效利用系数测算及阈值分析研究[D]. 兰州:兰州大学,2014. GU He. Coefficient and threshold calculation analysis of Gansu agricultural irrigation water use [D]. Lanzhou: Lanzhou University, 2014. (in Chinese)
23 KANG S Z, GU B J, DU T S, et al. Crop coefficient and ratio of transpiration to evapotranspiration of winter wheat and maize in a semi-humid region [J]. Agricultural Water Management, 2003, 59(3): 239-254.
24 JIANG X L, KANG S Z, TONG L, et al. Crop coefficient and evapotranspiration of grain maize modified by planting density in an arid region of northwest China [J]. Agricultural Water Management, 2014, 142: 135-143.
25 项国圣. 黑河中游张掖盆地地下水开发风险评价及调控[D]. 兰州:兰州大学, 2011. XIANG Guosheng. Risk assessment and regulation of groundwater development in Zhangye Basin of the middle reaches of the Heihe River [D]. Lanzhou: Lanzhou University, 2011. (in Chinese)
Irrigation Water Optimal Allocation Considering Stakeholders of Different Levels
LI Mo1JIANG Yao1,2GUO Ping1,2LI Jiang1
(1.CenterforAgriculturalWaterResearchinChina,ChinaAgriculturalUniversity,Beijing100083,China2.Chinese-IsraeliInternationalCenterforResearchandTraininginAgriculture,ChinaAgriculturalUniversity,Beijing100083,China)
Considering the complexities of nonlinearity, uncertainties and different interested parties in irrigation water allocation optimization, two models of different decision levels were established: one (upper level) was interval linear fractional programming (ILFP) model with the objective of maximizing irrigation water productivity, and the other one (lower level) was interval quadratic programming (IQP) model with the objective of maximizing irrigation outputs. On this basis, a linear fractional-quadratic bi-level programming (LFQBP) model was developed by integrating the decisions of the upper and the lower levels as a whole, in order to coordinate the benefits of different decision levels. LFQBP model was advantageous to make grain outputs and irrigation productivity reach a relatively high level and thus promoting the sustainable development of irrigation districts. All the three models were solved by using specific method, among which the key to the solution of IQP model and ILFP model was to transform the uncertain models into deterministic ones, and the key to the solution of LFQBP model was to transform the two-level model into single-level model. Then the developed models were applied to irrigation water allocation for grain crops in Yingke Irrigation District. Comparison among ILFP model, IQP model and LFQBP model demonstrated the characters of each model, and the optimization results showed that total water allocation amounts of the IQP model, ILFP model and LFQBP model were 63.01 million m3, 55.01 million m3and 60.34 million m3, respectively. Compared with IQP model, the crop output of LFQBP model was decreased by 0.44% while the irrigation productivity was increased by 4%, and compared with ILFP model, the crop output of LFQBP model was increased by 1.42% while the irrigation productivity was decreased by 7.64%. ILFP model and ILQBP model were more applicable in arid regions. The developed models reflected actual problems of irrigation allocation from different aspects, and the corresponding results were conducive to balance the benefits of decision-makers at different levels of an irrigation district.
irrigation water resources; optimal allocation; stakeholders; linear fractional-quadratic bi-level programming; uncertainty
2016-09-05
2016-09-28
国家自然科学基金重大研究计划集成项目(91425302)和水利部公益性行业科研专项(201501017)
李茉(1988—),女,博士生,主要从事农业水土资源管理研究,E-mail: limo@cau.edu.cn
郭萍(1963—),女,教授,博士生导师,主要从事水资源规划与管理、模型与优化和决策支持系统研究,E-mail: guop@cau.edu.cn
10.6041/j.issn.1000-1298.2017.05.025
S274
A
1000-1298(2017)05-0199-09
