计数原理与古典概率复习要点例析*

● 吴寅静

(余杭区教育局教研室 浙江杭州 311100)

计数原理与古典概率复习要点例析*

● 吴寅静

(余杭区教育局教研室 浙江杭州 311100)

文章对2017年数学高考中计数原理与概率的复习从知识、能力要求进行说明，并对每一个考点的主要考查方向以典型例题解读的方式进行分析.

计数原理;概率;二项式定理

1 知识内容

本单元的主要内容有：分类加法计数原理和分步乘法计数原理、排列与组合、二项式定理、杨辉三角与二项式定理.而古典概率主要内容有：事件、事件的关系与运算，互斥、对立、独立事件，概率与频率，古典概型.还有离散型随机变量及随机变量的分布列、均值、方差，独立重复试验的模型及二项分布.2 命题分析

计数原理、概率的内容在这几年浙江省的数学高考中变化很频繁，2014年之前是高考的必考内容，2015年、2016年则出现在自选模块中，2017年开始又进入高考的考试范围，考试的内容和难度也随着要求的变化而变化.根据2017年高考考试说明对这一部分内容的要求来看，这些内容在难度上属于适中，考试题型也以选择、填空题出现的可能性比较大.

从知识要求看，计数原理与概率的考查最多的是了解层次的内容，要求达到理解层次的主要是分类加法计数原理与分步乘法计数原理及二项式系数的性质，会用排列数公式、组合数公式解决简单的实际问题，会计算古典概型中事件的概率.

从能力要求看,高考中数据处理能力主要是通过排列、组合、概率与统计来实施的.关键是考生能对数据和随机数据进行提炼得出数据特征，同时考查考生能对众多数据进行合理筛选、选择模型、综合分析数据的思维能力.这对考生的模型建构、思维层次等也提出了较高要求.

3 典例剖析

3.1 计数原理重基础

很多考生一想到计数原理就是如何用排列组合公式计算出结果，对于分类加法计数原理和分步乘法计数原理则不够重视.从高考的考试要求来看，2个计数原理是概率的基础，也是考查逻辑思维能力、分类讨论思想、分析解决实际问题的基础，因此实际问题解决的起点要从2个计数原理开始，而不是直接从排列组合开始思考.

例1 1)在8张奖券中有一、二、三等奖各1张，其余5张无奖.将这8张奖券分配给4个人，每人2张，不同的获奖情况有______种(用数字作答).

(2014年浙江省数学高考理科试题第14题)

图1

2)如图1所示，某货场有2堆集装箱，一堆2个，一堆3个，现需要全部装运，每次只能从其中一堆取最上面的一个集装箱，则在装运的过程中不同取法的种数是______(用数字作答).

(2017年浙江省数学高考模拟卷第15题)

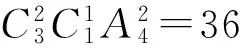
2)将5个集装箱标上不同的数字或字母，按第1个取的情况分类，再分别用枚举法即可得共10种.

评注 对计数原理的考查越来越回归本源，2个计数原理是解决排列与组合问题的基础，学会辨别分类还是分步，先分类还是先分步都是解决此类问题的关键.因此在针对这一内容的复习时重心要适当前移，避免发生重复和遗漏计算、用错公式的情况.

3.2 概率问题重热点

高考改革之后，对概率的考查范围逐渐缩小，但也越来越聚焦在古典概型上.古典概型问题既能考查考生对概率概念的理解程度，同时也能将计数原理中相关的知识进行综合，因此也成为概率内容命题的热点.

例2 1)有20张卡片，每张卡片上分别有2个连续的自然数k，k+1,其中k=0,1,2,…,19.从这20张卡片中任取1张，记事件“该卡片上2个数的个位数字之和(例如：若取到标有9，10的卡片，则卡片上2个数的各位数字之和为9+1+0=10)不小于14”为A，则P(A)=______.

2)有5本不同的书，其中语文书2本、数学书2本、物理书1本，若将其随机地摆放在书架的同一层上，则同一个科目的书都不相邻的概率是

( )

(2011年浙江省数学高考理科试题第9题)

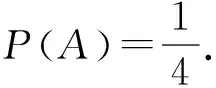
方法1 如何进行分类是解决这个问题的关键，其分类依据是从第1本书开始，这个方式虽然比较常规但也是解决实际问题中最为普遍的方式：

①若第1本书是语文书(或数学书)，第2本是数学书(或语文书)，则有4×2×2×2×1=32种可能；

②若第1本是语文书(或数学书)，第2本是物理书，则有4×1×2×1×1=8种可能；

③若第1本是物理书，则有1×4×2×1×1=8种可能.

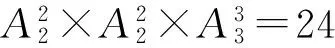
方法3 对立面的方式不唯一，进行排除的同时一定要关注重复计算的情况：

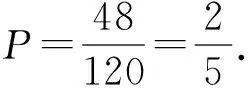
评注 概率试题的核心是古典概型，古典概型的概率问题常常会与排列、组合融合在一起，而解决排列、组合问题的关键是理清完成该动作是分类还是分步.

3.3 二项式定理重关键

二项式定理因其内容的原因其考查难度一直不大，最为常见的考查方向就是与二项式系数、二项展开式系数相关的问题，解决这类问题的关键就是通项公式.

(2011年浙江省数学高考理科试题第13题)

2)若将函数f(x)=x5表示为f(x)=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5，其中a0,a1,a2,…,a5为实数，则a3=______.

(2012年浙江省数学高考理科试题第14题)

分析 1)此题关键是弄清相关项的系数，通项公式在这里起到关键作用，即

从而

因为B=4A,所以

解得a2=4.又因为a>0,所以a=2.

2)解法1 此题的最高次数只有5，因此直接用通项公式提出关键项的系数，再进行对应系数相等的方式计算，即

解得

a3=10.

解法2 对f(x)=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5的2边连续对x求导3次，得

60x2=6a3+24a4(1+x)+60a5(1+x)2，

再运用赋值法，令x=-1得60=6a3，即a3=10.此方法不常用，但也是一种拓宽解题思路的方式.

解法3 通过对原函数形式的重新构造，转化成

f(x)=x5=(1+x-1)5=

(1+x)5-5(1+x)4+10(1+x)3-

10(1+x)2+5(1+x)-1,

从而直接得出a3=10.

评注 二项展开式中二项式系数、项的系数、常数项、有理项等归根结底就是二项展开式的通项公式.利用二项展开式的通项公式解决这类问题是关键，必须熟练掌握.同时二项式中对整个式子结构的重构、变形也是考查考生思维灵活性的一个方向，也需要在平时的复习中加以训练.

3.4 离散型随机变量及其分布列重应用

离散型随机变量及其分布列在2015年、2016年浙江省数学高考试题和自选模块中都没有作为考试内容，在2017年的高考考试说明中也基本以了解为主，这一块内容的复习以掌握基本概念、基本技能为重点，学会从相对简单的实际问题中提炼出问题模型并加以解决.

例4 1)随机变量ξ的分布列如表1所示：

表1 随机变量ξ的分布列

(2017年浙江省《数学高考考试说明》题型示例)

2)已知箱中装有4个白球和5个黑球，且规定：取出一个白球得2分，取出一个黑球得1分.现从该箱中任取(无放回，且每球取到的机会均等)3个球，记随机变量X为取出此3球所得分数之和；

①求X的分布列；

②求X的数学期望E(X).

(2012年浙江省数学高考理科试题第19题)

分析 1)出现2个变量即需要建立方程组，即

2)先确定X的可能取值有3，4，5，6，然后根据实际情况计算每一种情况的概率

由此可得X的分布并计算出数学期望

评注 离散型随机变量及其分布列从现有的情况来看,考查难度不会太大，但由于其具有一定的综合性和应用性，学生在理解随机变量X的取值及其概率计算时常常会出错，因此平时在这方面的复习还需关注.

4 精题集萃

1.将2个相同的白球、3个相同的红球、4个相同的黑球全部投入A,B,C这3个袋中，则无空袋的投放方法有

( )A.723种 B.865种 C.900种 D.1 204种

( )

3.甲、乙、丙3人各写一张贺卡随意送给丁、戊2人中的一人，则丁、戊2人中恰有一人收到一张贺卡的概率是

( )

4.将5个大小互不相同的球放入编号为1，2的2个盒子中，要求每个盒子里放入的球数不小于编号数，则不同的放球方法有______.

5.若(1-2x)2 017=a0+a1x+a2x2+…+

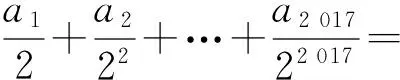
6.一个均匀小正方体的6个面中，3个面上标有数0，2个面上标有数1，1个面上标有数2，将这个小正方形抛掷2次，则向上的数之积的数学期望是______.

8.某市教育局组织中学生足球比赛，共有实力相当的8支代表队(含有一中代表队、二中代表队)参加比赛，比赛规则如下：

第1轮：抽签分成4组，每组2队进行比赛，胜队进入第2轮;第2轮：将4队分成2组，每组2队进行比赛，胜队进入第3轮;第3轮：2队进入决赛，胜队获得冠军.

现记ξ=0表示整个比赛中一中代表队与二中代表队没有相遇，ξ=i表示恰好在第i轮比赛时一中代表队与二中代表队相遇(其中i=1,2,3).

1)求ξ的分布列；

2)求Eξ.

参 考 答 案

8.解 1)ξ可取0，1，2，3,则

表2 随机变量ξ的分布列

2016-12-31；

2017-02-23

吴寅静(1974-)，女，浙江杭州人，中学高级教师.研究方向：数学教育.

O122.4

A

1003-6407(2017)04-44-04