平凡真功显 秒解素养现*
——由2017浙江省高中数学模拟卷17题说起
2017-06-05李学军曲文瑞
●李学军 曲文瑞
(平湖中学 浙江平湖 314200)
平凡真功显 秒解素养现*
——由2017浙江省高中数学模拟卷17题说起
●李学军 曲文瑞
(平湖中学 浙江平湖 314200)
作为数学教师要研究解题,要研究学生的解题,引导学生用数学的思维求思考和解决问题,去体会、体验在解题过程中的纠结和成功之后的快乐,实现真正意义的数学学习.文章结合2017年浙江省数学模拟卷中的一道填空题,深入挖掘考点,深刻探寻题源,为2017年的高考复习及数学素养的培养提供一种思考的方向.
解法;探源;教学;启迪
2016年12月17日浙江省考试院在全省范围内对参加2017年高考的学生进行了数学模拟测试,元济中学、湖州二中及平湖中学这3所学校结盟进行了网上阅卷,其中第17题的平均分为0.73,作为填空题的压轴题,真正发挥了对学生的选拔功能.
1 考题重现:似曾相识燕归来
题目 已知函数f(x)=x2+ax+b(其中a,b∈R),在区间(0,1)内有2个零点,则3a+b的取值范围是______(答案:(-5,0)).
人教A版教材必修1第87页明确指出:方程有实数根⟺函数与x轴有交点⟺函数有零点.
本题的实质是考查对函数零点概念的理解,并且融多种数学思想及解法于一体,这也是处理函数零点问题中最基本的想法.本题紧扣教材,无论是函数值范围的处理还是数形结合思想都源于教材.该题作为填空题的压轴题语言简洁,解题入口宽、层次多、区分度好,具有非常明显的“浙江风采”.
2 解法探究:横看成岭侧成峰
解法1 直接法
x2+ax+b=0的2个不相等的实数根为

图1
于是
设3a+b=z,如图1,由
得交点P(-2,1).
当直线3a+b=z经过点O(0,0)时,z=0;当直线3a+b=z经过点P(-2,1)时,z=-5,因此3a+b∈(-5,0).
点评 该题对于大多数考生来说要么基本没有想法,要么有想法但无行动.的确,在平时的高考复习中,学生对字母的运算是存在畏难心理的.另外,在平时复习的过程中也很少遇到.因此,该解法在考试的过程中,很少被考生想到,更不要说用好.
解法2 根的分布
因为函数f(x)=x2+ax+b(其中a,b∈R)在区间(0,1)内有2个零点,所以
整理得
接下来的处理方式有2种:
方法1 接下来走规划的路径,通过数形结合进行求解(同解法1).
方法2 把不等式组变形为

则
点评 通过数形结合的方式找出关于a,b的不等式组,大多数学生比较推崇方法1,因此在考场上,学生更喜欢走这样的路径.对于方法2来说,学生很难在短时间内想到,利用不等的关系进行消元,然后再利用函数的单调性,求出相关函数的上界或下界.
解法3 韦达定理
由题意设方程x2+ax+b=0的2个不相等的实数根分别为x1,x2,且0 x1+x2=-a,x1x2=b, 从而 3a+b= -3(x1+x2)+x1x2= (x1-3)(x2-3)-9. 因为0 -3 从而 4<(x1-3)(x2-3)<9, 即 -5<(x1-3)(x2-3)-9<0, 亦即 -5<3a+b<0. 点评 该解法把变量a,b用新的有范围的变量x1,x2来表示,根据x1,x2的范围来限制出3a+b的范围.这是一种非常值得推广的解题方法,但是这种解法说起来轻巧,在遇到实际问题时,马上进入解题通道的确有难度. 解法4 构造函数 3a+b=-3(x1+x2)+x1x2=x1(x2-3)-3x2, 因为0 从而 -5<3a+b<0. 点评 该解法把3a+b用一个有限定范围的新的变量表示出来,这种表述可以是相等的也可以是不等的.而本题恰恰是用不等关系表示,难度明显增加,解法4和解法2中的方法2有异曲同工之妙. 解法5 构造不等式 由题意可得下面的不等式组 因为f(0)=b,f(1)=1+a+b,所以 b=f(0),a=f(1)-f(0)-1, 从而 3a+b=3f(1)-2f(0)-3. -5<3f(1)-2f(0)-3<0, 即 -5<3a+b<0. 点评 把a,b用变量f(0),f(1)表示出来,f(0),f(1)的范围通过画图(如图2)可以看出,充分利用不等式的同向可加性,但在相加的过程中应尽可能利用整体的作用,否则容易把范围扩大. 图2 图3 解法6 数形结合 因为函数f(x)=x2+ax+b(其中a,b∈R)在区间(0,1)内有2个零点,所以方程x2+ax+b=0在区间(0,1)内有2个不相等的实数根. 设g(x)=-x2,h(x)=ax+b,如图3,g(x)和h(x)的图像在x∈(0,1)有2个交点,h(x)=ax+b的图像经过点P(3,t)和g(x)=-x2上一点M.当直线MP为N(1,-1)处的切线时,t=-5;当直线MP为O(0,0)处切线时,t=0,因此 -5 即 -5<3a+b<0. 点评 在研究等式、不等式解的时候,通常有2种思考方向:其一是构造一个函数,研究这个函数与x轴的交点问题;其二是构造2个函数,研究2个函数图像的交点问题.本题构造一个静态函数和一个动态函数,而3a+b恰好可以构造出具体的几何意义,这才是此题的本质所在. 源头1 已知:f(x)=x2+ax+b(其中a,b∈R). 2)已知函数f(x)在[-1,1]上存在零点,且0≤b-2a≤1,求b的取值范围. (2015年浙江省数学高考文科试题第20题) 源头2 设a,b∈R,函数f(x)=ax2+b(x+1)-2.若对任意实数b,方程f(x)=x有2个相异的实数根,求实数a的取值范围. (2015年浙江省高中数学联赛试题第16题) 源头3 已知b,c∈R,二次函数f(x)=x2+bx+c在(0,1)上与x轴有2个不同的交点,求c2+(1+b)c的取值范围. (2014年浙江省高中数学联赛试题第18题) 一道精彩的考试题目不仅体现在“表美”,更多的是“神美”的传递.通过对经典试题的钻研,在一定程度上能够引导教师根据实际调整教学内容以及根据教学内容选择恰当的教学手段和方法,进而会直接影响学生的数学学习能力的提升.这道填空压轴题虽然有着“入手易,解法多”的特点,但是在操作的过程中,部分学生仍然有力不从心的感觉.2017年浙江省数学高考文理科合卷,在复习教学时必须把握好教学的难易,需要落实基本概念,强化基本运算,需要落实基本方法,培养数学直观[1].因此,在高三的复习教学中我们应该更多关注以下几个方面: 1)以生为“心”. 在数学学习中“懂而不会,会而不全”的现象是非常普遍的,归根结底学生关注的焦点只是是否听懂、是否听会,而忽视了是否自己能够独立、高效地完成.在解题的过程中我们需要关注解法,但是作为数学教学,更需要学生亲身体验计算的过程,酸甜苦辣只有自己亲自尝过才知道其中的滋味. 2)以思为“先”. 在平时的学习过程中要经常对所学的知识和题型进行归纳,寻找规律和突破口.在平时的教学中要尽量留给学生足够的时间让学生读题、审题,在这个过程中读出若干个思维角度,审出题目的结构,理解问题的本质.教师和学生共同养成解题之后有反思的良好习惯,让学生既要知其然,更要知其所以然.通过反思养成对题目深入的探索,比如举一反三、一题多解、一题多变、多题一解,真正实现罗增儒先生倡导的“通过有限的典型例题的学习去领悟那种解无数道题的数学机智”. 3)以展突“破”. 解题是一种创造性的活动,作为数学的学习,积累一定的解题经验对以后解题过程中快速提取信息是大有裨益的,对一些相似的问题进行归纳总结之后,总会有些许的感悟,可以尝试对题目进行改编、拓展、推广,并在这个过程中巩固方法、辨别异同、提升能力.波利亚曾形象地指出:“好问题同某些蘑菇有些相似,它们大都成堆的生长,找到一个之后,你应当在周围再找一找,很可能就有几个.” 总之,题目是做不尽、探不完的.《庄子·养生主》中说:“吾生而有涯,而知也无涯.”通过这次浙江省考试院的模拟调研,笔者有一种感触:学生在考场上的思路探寻,教师在考后的解法探究,命题者在命题时的蓝图设计,俨然构成了一幅李白笔下的“举杯邀明月,对影成三人”的精彩且具有浓厚浙江风味的美妙画卷. [1]王红权.含绝对值的不等式问题复习研究[J].中学教研(数学),2016(12):29-34. 2016-12-20; 2017-02-16 李学军(1976-),男,吉林省德惠市人,中学高级教师.研究方向:数学教育. O123.1 A 1003-6407(2017)04-39-03
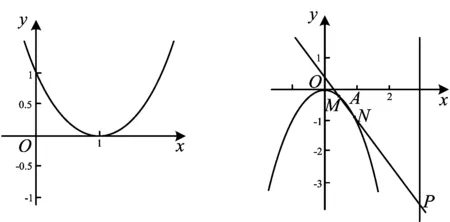
3 探源:那人却在灯火阑珊处
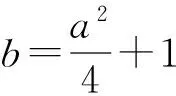
4 教学启迪:吹尽狂沙始到金
