平面解析几何备考复习策略*
2017-06-05叶莹莹浒山中学浙江慈溪315300苗孟义三山高级中学浙江慈溪315300
●叶莹莹 (浒山中学 浙江慈溪 315300) ●苗孟义 (三山高级中学 浙江慈溪 315300)
平面解析几何备考复习策略*
●叶莹莹 (浒山中学 浙江慈溪 315300) ●苗孟义 (三山高级中学 浙江慈溪 315300)
2017年浙江省数学高考命题是文理不分科后的第1次命题,文章在浙江省历年数学高考自主命题研究的基础上,结合考试院12月的测试卷,预测2017年高考平面解析几何部分的考查难度(过去的“文科起步、理科压轴”的梯度)、考查内容、命题特点、复习备考策略等.
解析几何;圆锥曲线;高考备考;复习策略
1 知识内容
平面解析几何是高中数学教学的核心内容之一,在高考数学中占有十分重要的地位,是历年高考的重点、热点和难点.主要考查直线方程,圆的方程,直线与直线、直线与圆、圆与圆的位置关系,简单的线性规划问题,圆锥曲线的定义、方程、性质,以及以椭圆或抛物线为载体,结合其他知识考查的综合性问题等.
2 试题分析
2017年是文理不分科后第1次高考数学命题,回顾历年浙江省数学高考试题和2017年省考试院测试卷可以看出,平面解析几何内容一般考查3~4个选择题和填空题、1个解答题.文理不分科后就这部分内容的考查,试题的难易度会有所调整,预测类似于过去的“文科起步、理科压轴”的梯度.
1)直线方程,圆的方程,直线与直线、直线与圆、圆与圆的位置关系,简单的线性规划问题,在历年高考中主要以选择题、填空题的形式出现,考查相关概念、基本公式及应用,简单的线性规划问题(包括含参、恒成立、能成立、整点)等.
2)圆锥曲线在历年高考中,试题呈现选择题、填空题、解答题3种题型,其命题特点:
①选择题、填空题多数在基本概念和性质上命题,考查学生推理论证能力与数形结合的能力,包括圆锥曲线的定义、标准方程、性质的应用,特别是渐近线、离心率等.
②解答题表述简洁明了,一题两问,由浅入深,起点低、落点高.第1问考查基础知识,第2问考查综合性问题,如面积、位置关系等,对知识提出了较高要求,对考生的直觉判断、探究思辨、转化化归、代数运算等方面提出新的挑战.
3 典题剖析
例1 1)“a=-2”是“直线l1:ax-y+3=0与直线l2:2x-(a+1)y+4=0互相平行”的
( )
A.充分不必要条件B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
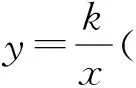
( )
A.与m有关 B.与a有关
C.与k有关 D.等于-1

( )
A.m<0 B.m>0

解 1)直线l1与直线l2互相平行的充要条件为

即
a=-2或a=1,
因此“a=-2”是“直线l1:ax-y+3=0与直线l2:2x-(a+1)y+4=0互相平行”的充分不必要条件.故选A.
2)由|logax|=m得
xA=am,xB=a-m.

yC=ka-m,yD=kam,
从而
因此直线CD的斜率只与k有关.故选C.

2t2-t+2m=0,
该方程表示一条直线,故关于t的方程在t≥0上有且只有1个实数解,分2类情况:

②令f(t)=2t2-t+2m,则f(0)<0,得m<0.

评注 文理不分科后,涉及直线的斜率与截距、直线平行与垂直的充要条件、直线方程的几种形式、交点、距离等的考题往往是送分题,在复习时要打实基础,提高计算的正确率.另外要注意与其他知识的结合考查.
例2 1)以(a,1)为圆心,且与直线2x-y+4=0与2x-y-6=0同时相切的圆的标准方程为
( )
A.(x-1)2+(y-1)2=5
B.(x+1)2+(y+1)2=5
C.(x-1)2+y2=5
D.x2+(y-1)2=5
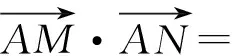
3)在平面直角坐标系xOy中,⊙C的方程为x2+y2+8x+15=0.若直线y=kx上至少存在一点,使得以该点为圆心、1为半径的圆与⊙C有公共点,则实数k的取值范围是______.
1)解 因为直线2x-y+4=0与直线2x-y-6=0的距离为

2)解法1 设直线l与⊙C的交点为M(x1,y1),N(x2,y2),则
(1+k2)x2-4(1+k)x+7=0,
从而
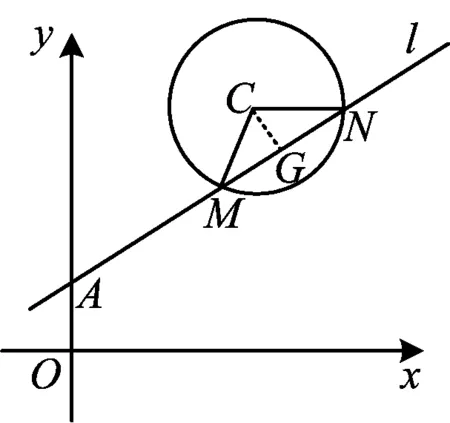
图1
解法2 如图1,取MN的中点为G,则CG⊥MN,由极化恒等式得

3)解 ⊙C的方程为
x2+y2+8x+15=0,
整理得
(x+4)2+y2=1,
这是一个以(-4,0)为圆心、1为半径的圆.又直线y=kx上至少存在一点,使得以该点为圆心、1为半径的圆与⊙C有公共点,则圆心C(-4,0)到直线y=kx的距离d≤2,即
解得
评注 研究直线与圆这2个基本图形,关键是抓住通性通法:用坐标法研究几何性质.在解题时一定要从数与形这2个角度入手,既要弄清图形的几何特征,又要熟练应用各种代数工具(解方程组、弦长公式、距离等),多方联想,选择适当的方法解题,减少计算量.特别是解决直线与圆的综合问题,处理直线与圆的弦长问题时多用几何法,即弦长的一半、弦心距、半径构成直角三角形;圆的切线问题的处理要抓住圆心到直线的距离等于半径,建立关系解决问题.第2)小题涉及到极化恒等式并没有出现在三角形中,但仍然适用,其本质就是圆的切割线定理.

2)已知实数x,y满足约束条件
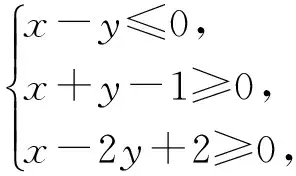
若目标函数z=2x-y+m的最大值为10,则实数m的值为
( )
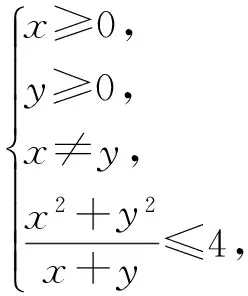
又zA=1,zB=3,zC=-1,于是目标函数z=x+y的取值范围为[-1,3].

图2 图3

(x-2)2+(y-2)2≤8(其中x+y≠0),

图4

评注 线性规划考查的题型以选择题、填空题为主,主要抓住以下3点:1)平面区域的画法:线定界、点定域(注意实虚线),是否为整数解等,避免失误的重要方法就是让二元一次不等式标准化;2)要注意数形结合思想的运用,目标函数的几何意义可从截距、斜率、距离等方面考虑,特别注意有时是距离的平方;3)要关注特殊点检验法.

解 1)若方程C表示椭圆,则
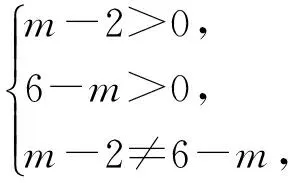
解得m∈(2,4)∪(4,6).
若方程C表示双曲线,则
(m-2)(6-m)<0,
解得m∈(-∞,2)∪(6,+∞).
2)设|AF|=a,|BF|=b,由抛物线定义知
2|MM′|=a+b.
由余弦定理得

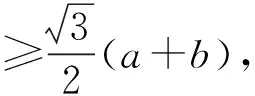
评注 这类题目往往是送分题,注重对圆锥曲线的定义与方程的考查,检测基本概念的理解和掌握程度,对不同曲线的几何性质又有不同的侧重考核要求.
1)求椭圆C的方程;

图5
2)如图5,过点M(0,m)(其中m>0)的直线与椭圆C交于点A,B,在直线y=-m上存在点N,使△NAB为正三角形,求m的最大值.
2)显然,直线AB的斜率存在,设其方程为
y=kx+m,
(1+5k2)x2+10kmx+5m2-5=0,
从而
Δ=100k2m2-4(1+5k2)(5m2-5).
设A(x1,y1),B(x2,y2),则
设线段AB的中点为P(x0,y0),则直线PN:
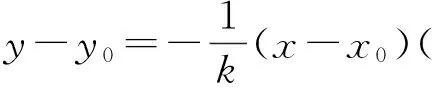
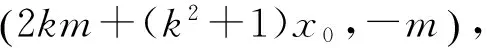



由△NAB为正三角形得

从而
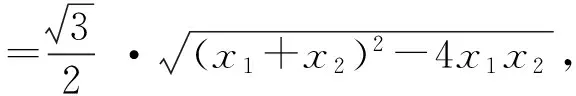
m2(2+5k2)2=15(5k2+1-m2),
得
令1+5k2=t,则
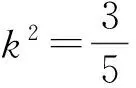
评注 解决解析几何综合问题的基本策略:1)利用方程思想,联立消元,结合韦达定理来解;2)设而不求,灵活运用曲线方程来处理;3)结合平面几何知识来处理,很多时候平面几何知识运用得好,可以大大减少计算量.从2017年浙江省数学测试卷解答题第21题第1)小题可以看出,对于程度较好的学生,最好多掌握一些“高考和竞赛接轨的部分,初等数学与高等数学的边缘部分”知识,可以秒杀很多难题.
4 精题集萃
1.设直线l1:(a+1)x+3y+2=0,直线l2:x+2y+1=0,若l1∥l2,则a=______;若l1⊥l2,则a=______.
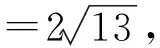
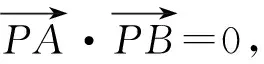


( )
A.8 B.10 C.12 D.15
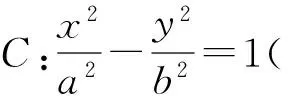
( )
7.已知定点A(-1,0)和B(1,0),动点P(x,y)在直线l:y=x+3上移动,椭圆C以A,B为焦点且经过点P,则椭圆C的离心率的最大值为
( )
1)求椭圆C的标准方程;
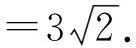
参 考 答 案
5.D 6.B 7.A
8.解 1)由题意得
解得a2=12,b2=4,因此椭圆的方程为
2)联立
消去y得
因为直线l与椭圆C交于不同的2个点A,B,所以
Δ=36m2-16(3m2-12)>0,
解得m2<16.设A(x1,y1),B(x2,y2),则x1,x2是方程(1)的2个根,则
从而


解之得m=±2.
由题意知,点P为线段AB的中垂线与直线y=2的交点.设AB的中点为E(x0,y0),则

即
y=-x-1,
令y=2,得t=-3.

即
y=-x+1,
令y=2,得t=-1.
综上所述,t的值为-3或-1.
2017-01-13;
2017-02-16
叶莹莹(1983-),女,浙江慈溪人,中学一级教师.研究方向:数学教育.
O123.1
A
1003-6407(2017)04-34-05
