基于K-means范例推理的救援物资需求预测

喻 慧，张 明，喻 珏

（南京航空航天大学民航学院，南京 211106）

基于K-means范例推理的救援物资需求预测

喻 慧，张 明，喻 珏

（南京航空航天大学民航学院，南京 211106）

针对低空救援过程中物资需求的模糊性，提出基于K-means范例推理法的物资需求预测。首先，对范例属性用粗糙集进行简约，并计算各属性的权重值；其次，将简约后的范例运用基于DB Index准则的K-means算法进行聚类分析；然后，计算当前范例与距离最小类中所有范例的相关系数，检索出相似度最大的目标范例，并根据目标范例的消耗量线性求解当前范例的需求量；最后，比较该方法与遗传优化BP算法的准确性，结果表明基于K-means范例推理的预测算法具有更高精度。

K-means；范例推理；粗糙集；需求预测

应急救援资源的需求预测受到诸多社会、环境等因素影响，具有很强的时效性和阶段性，同时灾情和物资需求信息具有模糊性和不确定性，灾情发生短时间内获取的信息极为有限，需结合对灾区历史统计数据挖掘基础上进行的资源需求分布预测，以保证预测的准确性。科学合理的应急救援物资需求预测不仅能给灾民提供充足的物资保障，而且能为应急调度策略的实施提供基础数据。因此，对应急救援物资需求进行合理预测是必不可少的救援环节。Guo等[1]针对应急物流的突发性、不确定性和复杂性等特点，提出基于模糊马尔可夫链的应急物资需求预测模型；Sun等[2]采用了两区域间模糊粗糙集方法来对应急物资需求进行预测；Hu[3]提出了一个保护灾害节点的基于公差模型的应急需求预测方法；Mohammadi等[4]提出了一种新的基于混合进化RBF神经网络的方法对紧急供应需求量进行预测研究。已有的相关研究并未考虑特征因素间的相关性，而且属性权重的确定在一定程度上仍依赖人的主观判断，大多忽略了对历史灾情数据的信息挖掘，缺乏将历史物资需求数据挖掘规则结合到应急物资需求预测中去，因而难以获得准确的应急救援物资需求。为使预测结果更为准确，本文提出一种基于K-means的范例推理法对低空应急救援物资需求进行预测。

一般来说，低空救援过程中首要解决的是效率和准确率问题，而历史灾情范例具有多属性、数据多而杂的特点，传统的范例推理法[5]在一定程度上会影响整个救灾效果，因此，提高范例检索效率及准确率是应急物资预测中急需解决的问题。为提高大数据的检索效率，首先对范例各属性运用粗糙集方法进行属性的简约，并计算各属性的权重值，然后将简约后的范例运用基于DB_Index准则的K-means算法进行聚类分析，再计算当前范例与距离最小类中所有范例的相关系数，检索出相似度最大的历史目标范例，并根据目标范例的物资消耗量以及各属性的权重值线性求解当前范例的物资需求量。该方法在一定程度上提高了范例的检索效率与需求预测精度。

1 基于DB Index准则的K-means聚类算法

K-means算法采用欧式距离作为两个样本聚类评价指标，其基本思想是：随机选取历史范例数据库中的k个点作为初始聚类的中心，根据各范例到k个中心的距离将其归类到距离最小的类中，然后计算各个类中范例距离的平均值，更新每个类的中心，直到聚类中心不再发生变化。其目标是将范例数据库中的范例分成若干个类，使得同一类范例间的相似度尽可能大，不同类范例间的相似度尽可能小。

本文使用DB Index准则评估k的最优取值，获得数据的分类，为下文找出与当前范例相似度最高的历史范例提供数据支持，DB Index准则评估步骤如下：

1）类内平均离散度

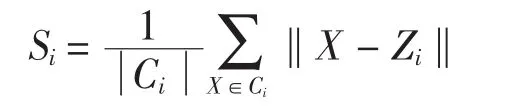
其中：Zi是Ci类的类中心；表示Ci类样本数；

DB Index准则是DBk值越小，说明分类效果越好。

2 基于范例推理的物资需求预测

2.1 范例推理预测方法

2.1.1 基于粗糙集的范例属性简约

针对灾情范例的模糊性与不确定性，首先需对范例属性进行规整，得到简化后范例特征以提高数据的处理效率。

粗糙集理论[6]是波兰数学家Z·Pawlak于1982年提出的，其在处理不完整数据和不精确数据方面具有独特优势。设信息系统S=（C，B），C={C1，C2，…，Cn}为范例数据库，Cn为第n个范例，B为范例属性所组成的集合，即B=F∪D。其中，F={f1，f2，…，fm}为条件属性集，即和地震有关的情景特征因素（如总人口、总面积、震级、震源深度、最高烈度、受灾人数、伤亡人数、砖混比例）信息集，fm为第m个属性的信息；D={D1，D2，…，Di}为决策属性集，即主要应急物资需求集，Di为第i类物资的需求量，在本文中D0表示耐用品需求量，D1表示消耗品需求量。给定各条件属性阈值，范例条件属性值满足阈值要求为1，否则为0，按此规则生成0-1信息表。如果C/ind（F）=C/ind（F-{fm}），则属性fm可以约简，否则不可约简。

2.1.2 属性权重值计算

在不同的决策环境下，各条件属性对决策结果会有不同程度的影响，在此需计算出简约后范例的各条件属性对物资预测结果的影响程度，用属性权重值ωj表示。令条件属性集F={f1，f2，…，fm}的影响权重集为{ω1，ω2，…，ωm}，且满足

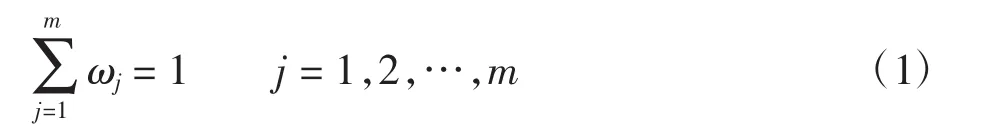
在不同的决策环境下，条件属性对决策输出会有不同影响。令n（f）表示范例在条件属性为f时的取值。当n（f）在范例库C={C1，C2，…，Cn}中的分布差异较大时，说明该条件属性对分类判别作用大，应赋予较高权重值；反之，当n（f）在分类中的分布差异较小时，说明该条件属性对分类作用不大，应取较小的权重值。范例Ci在条件属性fj下的取值n（fj）为该案例在特征因素fj下的隶属度函数，并有

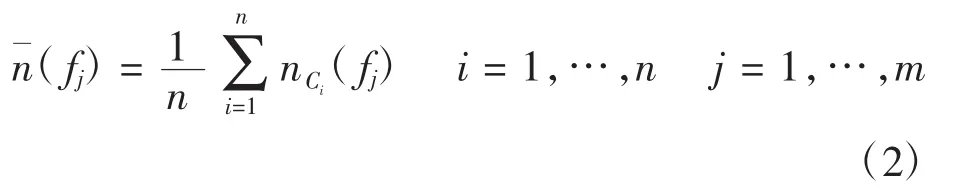
均方差为

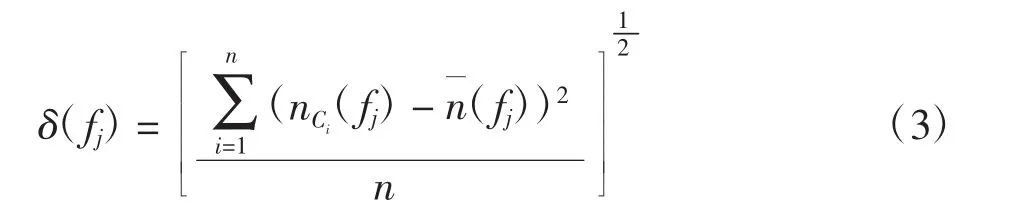
则可求得各特征因素的权重ωj为

2.1.3 范例相似度计算

根据K-means算法的分类，找出K个聚类中心点距离当前范例最近的一类，再比较当前范例与该类中的每一个范例的相似度，找出相似度最大历史灾情范例，为当前范例的物资需求预测提供数据基础。

本文采用相关系数对范例间的相似度进行计算，其中相关系数的定义如下

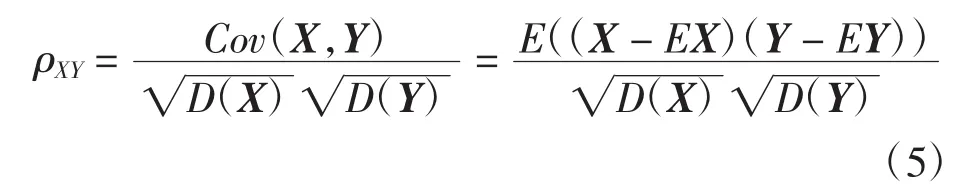
相关系数是衡量随机向量X与Y相关程度的一种方法，取值范围是[-1，1]。相关系数的绝对值越大，则表明X与Y相关度越高。

2.1.4 覆盖度计算

规则覆盖度的直观意义就是符合某个决策规则的对象数占整个论域空间对象数的比例。

2.2 应急救援物资需求预测

假设相似度最大的历史目标范例的总人口、震级、伤亡人数及砖混比例分别为P1、P2、P3和P4，耐用品和消耗品的供应量分别为N1、N2，条件属性f1、f3、f7、f8的权重值分别为ω1、ω3、ω7、ω8，当前范例的总人口、震级、伤亡人数以及砖混比例分别为P1′、P2′、P3′和P4′，则当前范例耐用品和消耗品的需求量N1′和N2′分别为

3 算例分析

3.1 范例属性简约及权重值计算

选取2008—2012年22个灾情数据[7]作为训练样本，如表1所示，其中，条件属性为总人口（人）、总面积（km2）、震级（级）、震源深度（级）、最高烈度（级）、受灾人数（人）、伤亡人数（人）、砖混比例，决策属性为耐用品需求量D0（kg）、消耗品需求量D1（kg）。将样本的条件属性按表2的规则进行离散化处理，超过阈值的属性值设为1，否则设为0。

离散化后，属性f1、f2对各范例的属性值相同，故只保留属性f1；同样，属性f3、f4、f5对各范例的属性值相同，保留属性f3；属性f6、f7对各范例的属性值相同，保留属性f7。属性简约后得到新的条件属性集为F= {f1、f3、f7、f8}。再按式（4）计算出当前条件属性集中各属性的权重值分别为ω1=0.13、ω3=0.36、ω7=0.31、ω8=0.20，权重值越大，说明该条件属性对分类判别的作用越大，反之，权重值越小，说明该属性对分类判别的作用越小。

表1 范例信息Tab.1 Case information

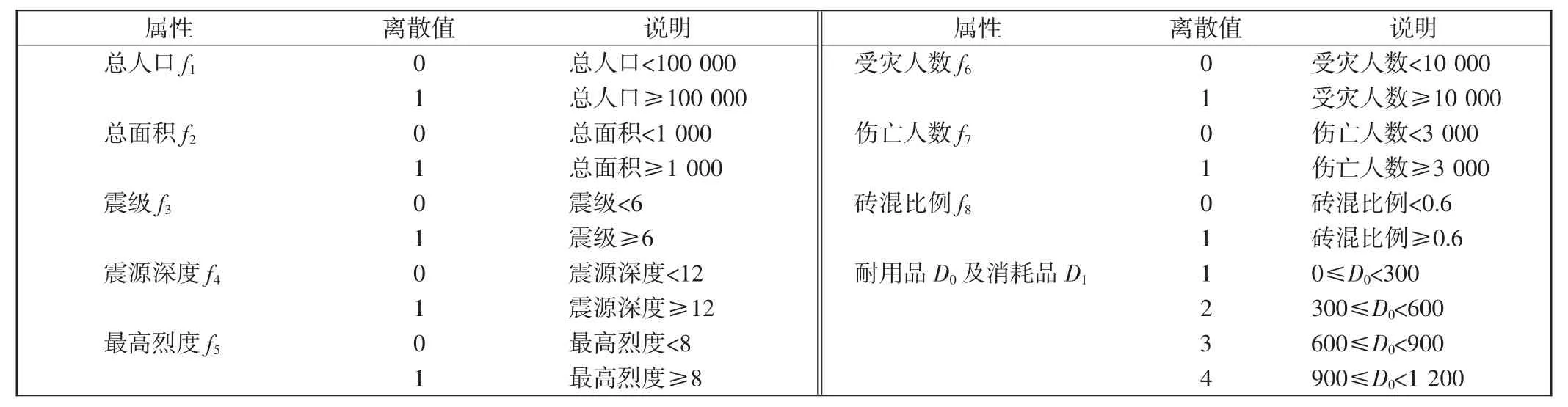
表2 离散化处理规则Tab.2 Discrete processing rule

利用粗糙集属性简约方法，属性的维数从8维降到了4维，可以有效降低灾害范例冗余属性，提高运行效率，在不损失有效信息的前提下降低了数据处理的规模和存储空间；而简约后的范例各属性对应急救援物资需求预测结果的影响也不同，因而再利用粗糙集的属性重要度，确定约简后的范例属性权重值，以克服由专家决定关键属性和权重的主观性，提高了应急资源需求预测的效率和精度。

3.2 物资需求决策规则覆盖度计算

经过粗糙集简约所得决策规则如表3所示。搜集400条历史灾情数据构建范例数据库，统计各规则发生频率如下。

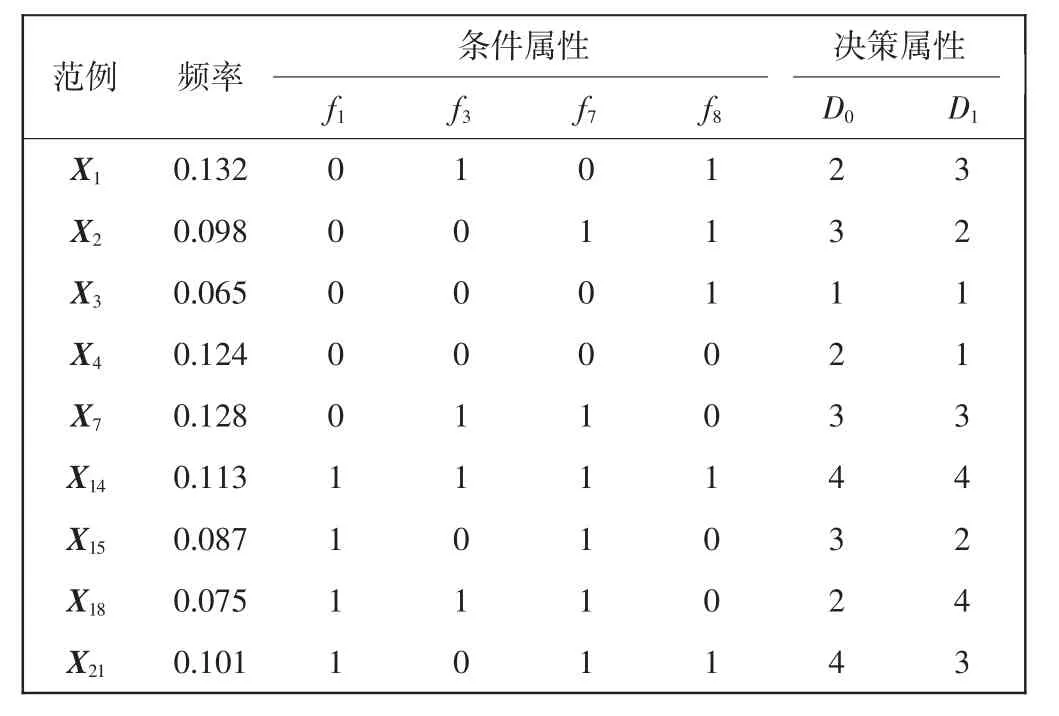
表3 物资需求决策规则Tab.3 Decision rule of material demand

对表3中第一行可分析出，当总人口小于100000人、震级≥6级、伤亡人数＜3 000人、砖混比例≥0.6这4个条件都满足时，对应初级救援配送方案为：耐用品D0的物资配送量为300～600 kg，消耗品D1的物资配送量为600～900 kg，规则依此类推，可得出不同的低空应急救援快速响应预案。

覆盖度等于各规则频率之和，当条件覆盖度大于90%时，则该规则成立[8]。通过表3中各规则出现的频率，计算得出满足该决策样本数占整体样本数的92.3%，即规则覆盖率为92.3%，说明该规则成立，可用于实际救援，也为后续范例物资需求量预测提供理论依据。

3.3 范例聚类分析及物资需求预测

运用K-means算法将400条历史灾情数据[9]的范例样本进行分类，其结果如图1～图3所示。

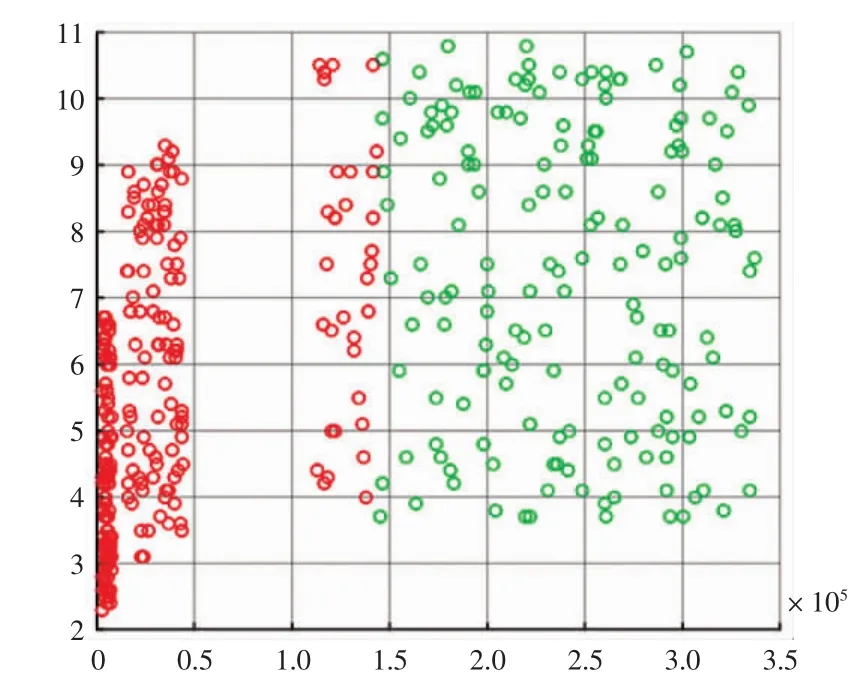
图1 k=2时的范例聚类结果Fig.1 Case clustering result when k=2

图2 k=3时的范例聚类结果Fig.2 Case clustering result when k=3

通过对比以上实验聚类结果，可明显看出k=2时范例聚类效果太分散，k=4时的范例聚类结果中各分类重叠区域较大，当k=3时范例聚类效果较好，分类清晰可见。故选取k=3作为分类数。

图3 k=4时的范例聚类结果Fig.3 Case clustering result when k=4

令当前范例X22=（129 320，6.3，4 967，0.833），从而计算出X22与上述4个中心点的欧式距离分别为155 114.910、31 896.365、104 617.455、376 667.762。通过分析可知，当前范例X22与第二类中心点O2的距离最近，故将当前范例视为第二类，然后运用Matlab将属于第二类的数据筛选出来，并将当前范例X22与第二类中的每个范例运用式（5）进行相似度计算。计算结果中最大的相关系数为0.999 983 050 183 65，其对应的历史案例是X141=（136 455，8.4，4 418，0.783），通过查找范例数据库数据可知，历史范例X141对耐用品和消耗品的物资需求量分别为1 100 kg和700 kg，故结合式（4）求得各条件属性权值ω1=0.13、ω3=0.36、ω7=0.31、ω8=0.20，利用线性相关算法对当前范例的耐用品和消耗品的物资需求量进行预测，结果分别为D0=1 049 kg，D1=668 kg。

3.4 范例推理预测法与遗传优化BP预测法的比较

从400条历史范例中选出X22=（129320，6.3，4967，0.833）作为当前范例，已知其对耐用品和消耗品的物资需求量分别为1 000 kg和600 kg，运用基于K-means的范例推理预测法及遗传优化BP预测法[10]的相同权值（即ω1=ω3=ω7=ω8=0.25）和不同权值（即ω1=0.13、ω3=0.36、ω7=0.31、ω8=0.20）时的相对误差，如表4所示。

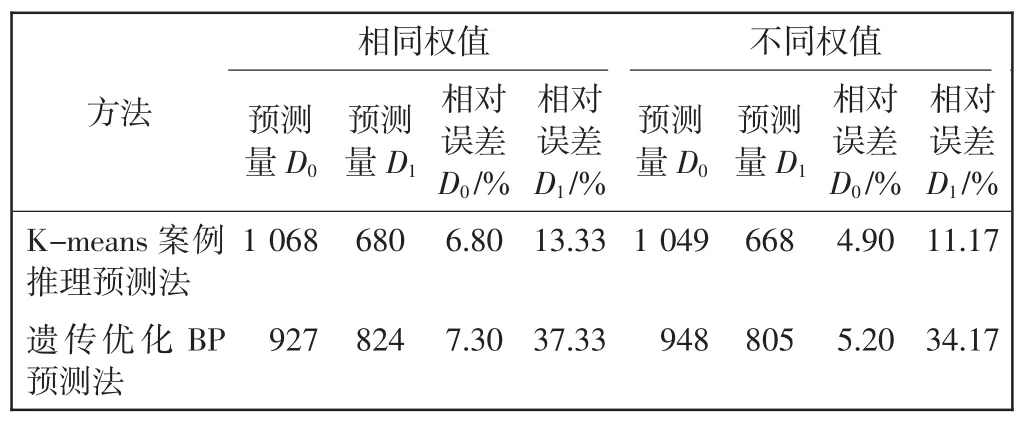
表4 K-means范例推理预测法与遗传优化BP预测法的比较Tab.4 Comparison between K-means CBR method and genetic optimization BP algorithm

由表4可以看出，根据属性重要度计算的权重值，预测相对误差较平均权重值下的相对误差明显要小，且预测结果较为稳定，运用基于DB_Index准则的K-means聚类方法对历史灾情范例进行先分类后处理，不仅提高了运行效率，也使预测结果更具准确性。

4 结语

本文将范例推理理论和基于DB_Index准则的K-means聚类算法引入低空救援物资需求预测领域，在对历史范例的特征属性进行有效约简的基础上，再利用K-means聚类算法对大量历史灾情数据进行分类，检索出相似度最高的历史范例，根据历史案例的物资消耗量及各属性的权重值来线性推测当前相似范例的物资需求量。范例推理理论和基于DB_Index准则的K-means聚类算法的结合不仅提高了范例的检索效率，同时也提高了预测精度，使其成为应急救援物资需求预测的新方法。

[1]GUO Z,QI M.Research on the Demand Forecast of Emergency Material Based on Fuzzy Markov Chain[C]//E-Product E-Service and E-Entertainment(ICEEE),2010 International Conference on.IEEE,2010:1-4.

[2]SUN B,MA W,ZHAO H.A fuzzy rough set approach to emergency material demand prediction over two universes[J].Applied Mathematical Modelling,2013,37(10/11):7062-7070.

[3]HU Z H.Relief Demand Forecasting in Emergency Logistics Based on ToleranceModel[C]//InformationManagementandEngineering(ICIME), 2010 The 2nd IEEE International Conference on.IEEE,2010:451-455.

[4]MOHAMMADI R,GHOMI S M T F,ZEINALI F.A new hybrid evolutionary based RBF networks method for forecasting time series：A case study of forecasting emergency supply demand time series[J].Engineering Applications of Artificial Intelligence,2014,36：204-214.

[5]夏兴生,朱秀芳,潘耀忠,等.基于历史案例的自然灾害灾情评估方法研究[J].灾害学,2016,31(1):219-225.

[6]张文修，吴伟志，梁吉玉.粗糙集理论与方法[M].北京：科学出版社，2003：2-10.

[7]郑通彦,冯 蔚,郑 毅.2014年中国大陆地震灾害损失述评[J].灾害学,2015,25(2):88-97.

[8]夏叶娟.基于粗糙集和决策树的规则提取方法研究[D].南昌：南昌大学,2008.

[9]中国地震局监测预报司.中国大陆地震灾害损失评估汇编[M].北京:地震出版社,2001.

[10]吴雪莲.自然灾害应急物资需求预测方法研究[D].合肥:中国科学技术大学,2012.

（责任编辑：杨媛媛）

Low altitude rescue demand forecasting based on K-means CBR

YU Hui,ZHANG Ming,YU Jue
（College of Civil Aviation,Nanjing University of Aeronautics and Astronautics,Nanjing 211106,China）

Aiming at the fuzziness of supplies demand in the process of low altitude rescue,a CBR（case based reasoning）prediction algorithm based on K-means is proposed.Firstly,the attributes of case are reduced through rough set, the weight values of attributes are calculated.Next,a cluster analysis is made on simplified case through DB Index K-means algorithm;then,correlation coefficient is calculated between the current case and each case in the nearest group,retrievaling the target case with maximum similarity.Finally,according to the supplies of target case,demand of the current case is obtained.A real seismic data is conducted to compare the accuracy of the current approach and genetic optimization BP algorithm.Result shows that the K-means CBR algorithm has higher precision.

K-means;CBR;rough set;demand forecasting

V355.2

A

1674－5590（2017）02－0055－05

2016-09-05；

2016-10-13

国家自然科学基金项目（U1233101，7127113）；中央高校基本科研业务费专项（NS2016062）

喻慧(1992—)，女，湖北孝感人，硕士研究生，研究方向为低空救援、空中交通智能化.