基于GMM的单航空公司安检区旅客到达模型

于之靖，包邻淋，，罗 谦

（1.中国民航大学电子信息与自动化学院，天津 300300；2.中国民航局第二研究所，成都 610041）

基于GMM的单航空公司安检区旅客到达模型

于之靖1，包邻淋1，2，罗 谦2

（1.中国民航大学电子信息与自动化学院，天津 300300；2.中国民航局第二研究所，成都 610041）

运用高斯混合分布模型对某航空公司安检区旅客到达分布进行拟合分析。采用极值聚类的方法获取EM求解算法的初验分布，经过多次迭代后求得参数解。在实验环节采用某航空公司真实值机输出数据进行实验验证，结果表明GMM对单航班安检区旅客到达分布的拟合精度达到90%以上，比常用拟合方法提高了15%以上。在分峰不明显的情况下，E value-GMM与K means-GMM拟合精度相比提高了5%左右。

单航空公司；高斯混合分布；EM算法；极值聚类

近年来中国航空业发展迅速，民航局统计数据显示，截至2014年底中国航班总量达到3 356 756架次，中国成为仅次于美国的全球第二大航空运输体系。中国的航空运力保持着强劲的增长趋势，截止到2016年8月，中国航空总座位数增加到6 520万个，与去年同期相比增加了12%，每天增加18.2万个座位。随着航空运输量的增大[1-2]，机场航站楼离场系统面临前所未有的压力。旅客离港服务过程中安检工作复杂且繁琐，在整个离港服务工作流程中占有重要位置。安检服务工作流程的优化成为旅客离港服务工作流程优化中不可缺少的一部分。

研究航站楼离场流程首先需对航站楼旅客聚集行为进行研究分析[3]，同理，安检服务流程同样需要优先研究安检旅客聚集规律。对于旅客聚集规律国内外学者进行了多方面的研究。Profillidis V.A.等[4]提出采用模糊理论的计量经济模型来估计希腊机场的航站楼旅客流量，通过客流量来调整系统资源优化服务流程。Bandeira[5]和GCL Bezerra等[6]主要通过对大型机场的旅客数据进行分析研究，通过对旅客在航站楼值机、安检区域的排队时间、服务时间等各项服务指标进行定性和定量的分析，对各大机场的旅客服务水平进行有效的预测评估。Akdere Mtich等[7]提出通过复杂时间的分割处理原理，对分布式环境进行分割查询优化处理，根据旅客吞吐量和航站楼资源设备对旅客的到达聚集行为进行预测和优化。上述研究通过分析旅客到达的分布情况采用多种方法建立某个区域的旅客聚集预测模型。在安检环节中旅客到达行为即受到整体离港系统旅客到达速率的影响也受到值机区环境因素的影响，所以安检区旅客到达分布不能直接得到。为建立安检区旅客到达的预测模型需对安检区旅客到达的分布情况进行分析。

航站楼旅客到达数据是由多个航空公司旅客数据叠加组成，本文主要是对单航空公司安检区的旅客到达分布进行数据拟合分析，为航站楼安检区旅客到达预测分析研究提供理论依据。文中选取单航空公司旅客值机输出数据作为安检区旅客到达数据进行研究分析。采用极值划分法对值机输出数据进行聚类分析，运用EM算法对混合分布进行求解。采用常用拟合分布函数和GMM对旅客数据进行拟合对比分析。实验结果表明，GMM拟合精度达到90%以上，相比常用拟合函数精度提高了15%以上。在分峰不明显的情况下，E value-GMM与K means-GMM的拟合对比表明精度提高了5%左右。

1 高斯混合模型的建立

研究表明，机场旅客的到达速率受到航班起飞时间、航班量等多方面因素的影响[8]。为建立安检区旅客到达分布模型，本文主要研究的是单航空公司航班离港时刻驱动的安检旅客到达分布模型。统计表明，大多数旅客到达航站楼进行值机后将直接进入安检区。因此可简单认为值机区域旅客流的输出即为安检区旅客流的到达，故通过值机输出数据的分析可获取安检区域旅客的到达规律。图1为某日双流机场某航空公司安检区旅客到达规律的概率分布统计。横轴表示时间，原点为0：00时刻，1代表24：00；纵轴表示安检区旅客的平均到达率。

常用的概率密度分布函数包括：高斯分布、伽玛（Gamma）分布、瑞利分布以及爱尔朗（Erlang）分布等，都要求所拟合系数的概率分布具有单峰形式，即只有一个极大值。但实际应用中，由图1可见旅客在安检区的到达概率密度分布随时间变化呈多峰形态。在数据分布拟合中很难把这种复杂的多峰分布通过单重的概率分布函数表示出来，因此多重高斯混合分布采用多个单重高斯分布叠加的方法对概率分布函数进行拟合。高斯混合分布能很好地拟合多峰形态的概率分布函数，具有理论分析的可解析性和较强的逼近能力。

图1 安检区旅客到达概率分布Fig.1 Passenger arrival distribution in security area

定义1 高斯混合分布[9]是由两个或两个以上子体高斯分布组合而成。假设样本数据的观测值为x={x1，x2，…，xn}（n为观测值的样本数），x服从混合分布G（x），且G（x）分布由k个独立的单重高斯分布Gi（ui，σi）（i= 1，2，…，k）组合而成。样本观测值x={x1，x2，…，xn}是基于k个高斯分布产生的样本值的集合，因此其高斯混合分布的累积分布函数表达式为

其对应的密度分布函数为

综上所述，高斯混合模型（GMM,Gauss mixture model）表达式为

其中：Θ={a1，…，an；u1，σ1，u2，σ2，…，un，σn}；ai为各分量的混合系数；ui为单重高斯分布的均值；σi为单重高斯分布标准差；n为混合分布分量个数。

2 高斯混合模型求解

在两重或两重以上混合高斯分布模型中存在的未知参量较多，且参数估计求解难度较大。常用的参数估计方法主要有最小二乘法、矩估计法、极大似然估计等方法。运用最小二乘法、矩估计和极大似然方法进行运算产生的都是超越方程组，求解繁杂，难以求解估计参数的准确值。为避免传统参数估计方法计算的复杂过程，降低混合模型参数估计难度，选用EM算法从非完整数据中对参数进行最大似然估计，通过循环迭代得到最佳的估计参数值。

EM算法具有易收敛、收敛速度快和易于实现的特点。因此，本文利用EM算法对高斯混合分布密度函数模型进行求解，算法的极大似然估计原则可通过迭代算法实现[10]。在EM算法步骤中需对初始数据进行聚类运算获取初验分布，目前常用的典型聚类分析方法主要包括划分方法、层次方法、基于网格的方法、基于密度的方法和基于模型的方法等。k均值聚类是最著名的划分聚类算法，由于简洁和高效使其成为所有聚类算法中使用最广泛的，其求解方法和步骤如表1所示。

表1 EM算法步骤Tab.1 Steps of EM algorithm

定义2 K聚类高斯混合模型（K means-GMM，K means-Gauss mixture model），是指给定一个数据点集合，采用K均值聚类根据某个距离函数反复把数据分入k个聚类中。通过K均值聚类分析获取初验分布，通过迭代运算后得到的高斯混合模型。

定义3 极值聚类高斯混合分布（E value-GMM，extreme value Gauss mixture model），是指给定一个数据点集合分布服从连续多峰函数f（x），由函数的极小值点对应多峰曲线的谷值，极大值对应多峰曲线的峰值和两个极小值之间必定存在一个极大值，通过两个极小值点对时序段的分割进行数据组的分类，使每个数据分类簇对应的数据分布曲线有且仅有一个极大值。

由于旅客到达数据为已知的多峰形态[11]，采用高斯混合分布进行拟合分析。对旅客到达数据进行聚类分析，根据定义2这里采用极值聚类方法进行聚类分析，得到样本数据的先验分布函数。

3 拟合结果分析与验证

本文选取的实验软硬件环境为：Matlab 7.12.0（R2011a），PentiumⅣ3.6GHz CPU，2GB内存。针对安检旅客到达的高斯混合分布研究，随机选取某航空公司在两个不同航班分布下任意某天的旅客到达概率分布作为数据来源。

3.1 常用拟合函数与GMM拟合效果对比

运用Matlab的核密度函数得到两个不同航班分布下随机某天安检区旅客到达的概率密度分布x1和x2。采用高斯混合分布、伽马分布、瑞利分布等常用的数据拟合函数对不同航班分布下不同时间段旅客到达数据进行拟合分析，得到的拟合图如图2所示，其中：曲线1为高斯分布拟合曲线，2为伽马分布曲线，3为瑞利分布曲线，4为高斯混合分布拟合曲线。

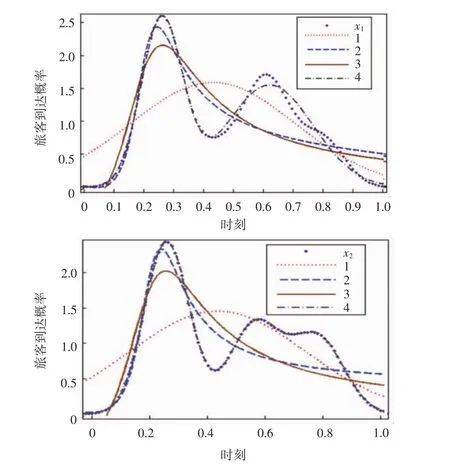
图2 不同航班分布下旅客到达数据拟合效果图Fig.2 Different flight passengers arrival distribution fitting chart

一般情况下用拟合优度来衡量模型拟合值和真实值之间的差值[12]，度量拟合优度的统计量可以是可决系数（亦称确定系数）R2、残差平方和、相关系数等。由于可决系数R2为综合度量回归模型对样本观测值拟合优度的度量指标，这里选取可决系数R2作为检验拟合优度的指标。

定义4 可决系数为

其中：RSS为回归平方和；TSS为总变差；ESS为残差平方和；R2的取值范围是[0，1]。对于一组数据，TSS是不变的，所以RSS值变大时，R2值变大，ESS值变小时，R2值变大。拟合优度R2值越小，自变量对因变量的解释程度越高，自变量引起的变动占总变动的百分比高，观察点在回归直线附近越密集[13]。将上述拟合函数与实际到达数据进行拟合优度分析得到的可决系数R2值如表2所示。

表2 拟合函数关系式及可决系数R2表Tab.2 Fitting function relation and R2

由于GMM是由多个单重高斯分布组合而成的函数式，能够依据单重高斯分布的参数调整很好地拟合数据曲线的多峰形态；一般常用拟合函数相对子高斯混合分布函数形态较为单一、有且仅有一个峰值、仅能对单峰数据曲线进行参数调整。由于高斯混合分布形态的多样性，因此采用高斯混合分布模型获得函数关系式的拟合优度在90%以上，能很好地拟合安检区的旅客到达分布，与一般常用的拟合函数相比拟合优度提高了15%以上。

3.2 Kmeans-GMM与Evalue-GMM拟合效果对比

运用Matlab核密度函数得到不同航班分布下安检区旅客到达的概率密度分布，如图3和图4所示的x1和x2数据，图3中的曲线1、2为不同航班分布下采用常用K means-GMM的初验分布数据簇曲线，图4（a）中的曲线1、2和图4（b）中的曲线1、2、3为不同航班分布下采用E value-GMM的初验分布数据簇曲线。

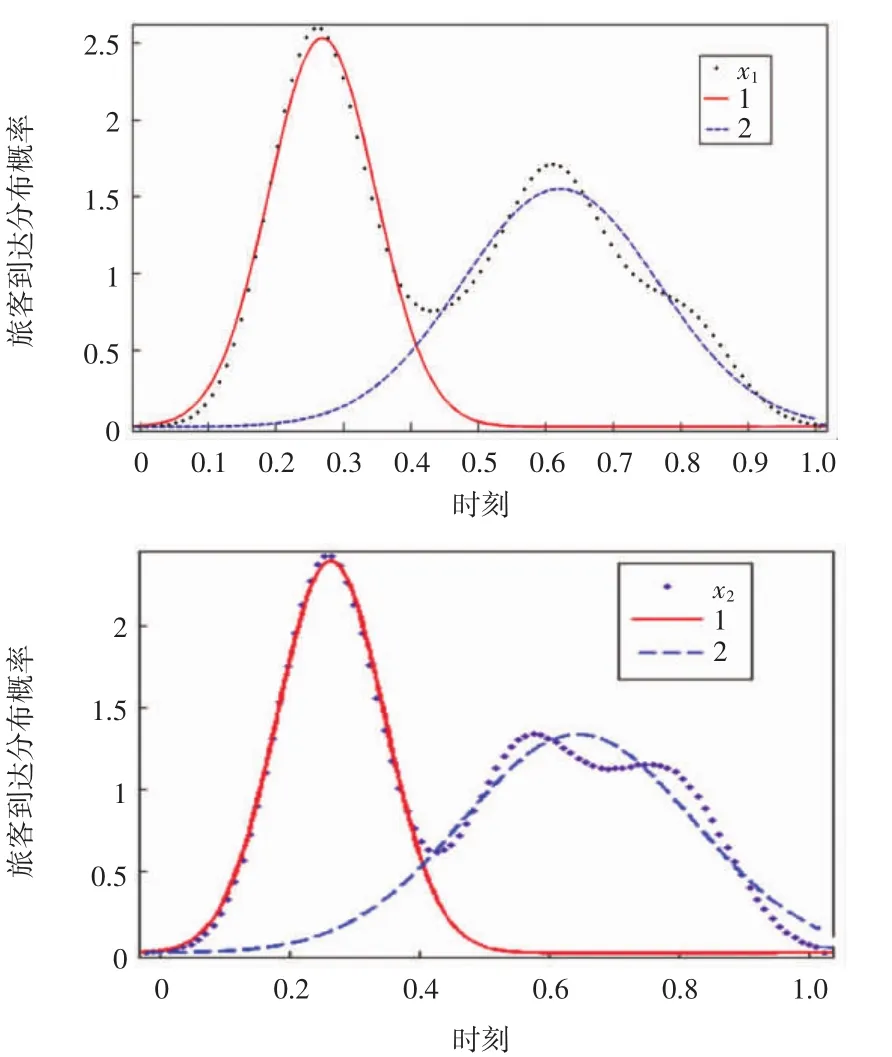
图3 K means-GMM初验分布Fig.3 K means-GMM preliminary distribution

图4 E value-GMM初验分布Fig.4 E value-GMM preliminary distribution

通过K means-GMM初验分布（如图3所示），从初验分布的数据簇中可得到高斯混合分布的函数关系式为

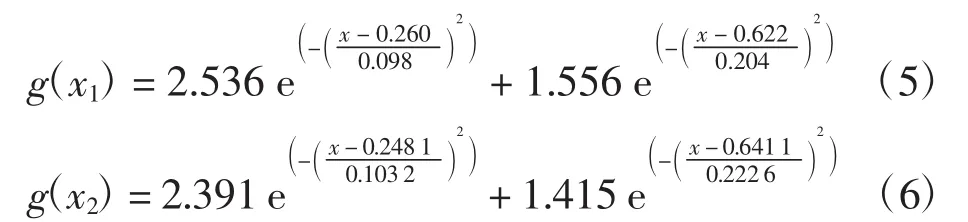
通过E value-GMM的初验分布（如图4所示），从初验分布的数据簇中可得到高斯混合分布的函数关系式为

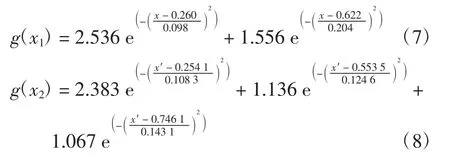
运用Matlab编写EM求解迭代算法，对各数据簇的初验分布参数进行迭代运算，得到GMM的参数估计值。采用定义4中可决系数R2值衡量拟合函数的拟合优度，计算所得数据如表3所示。

表3 K means-GMM与E value-GMM拟合优度表Tab.3 K means-GMM and E value-GMM fit table

综上所述，E value-GMM多适用于分峰比较明显的数据拟合。对于机场航班旅客到达规律的研究由于计划航班时刻的安排，存在一些分峰不明显的情况，在K means聚类分析时会使分类不够细致导致得到的拟合函数存在一定误差。在E value-GMM中，对分峰不够明显的情况可以很好地获取聚类。因此根据可决系数拟合优度值表明：采用GMM获得函数关系式的拟合优度均在90%以上，能很好地拟合安检区的旅客到达分布。在分峰不明显的情况下，采用E value-GMM的拟合精度比K means-GMM的拟合精度R2提高了5%左右，提高了模型的拟合优度。

4 结语

本文研究的是单航空公司安检区的旅客到达规律，并采用高斯混合分布对旅客到达数据进行拟合分析。在高斯拟合的参数求解过程中采用EM算法进行迭代运算，在EM算法的初验分布中提出采用极值聚类的方法获取初验分布参数。实验分析表明，采用GMM的拟合精度均达到了90%以上，相比一般常用拟合分布函数的拟合精度提高了15%以上。将E value-GMM与K means-GMM相比，实验结果表明E value-GMM拟合精度提高了5%左右。

本文所研究的仅为单一航空公司旅客到达的拟合分析，而在实际生产过程中对安检区服务流程的优化不仅仅需要对安检区旅客到达进行拟合分析，还需要对旅客到达行为进行准确的预测。因此下一步的研究工作则是通过高斯混合分布的拟合参数分析预测在某一安检区内的旅客到达规律。

[1]王 勇.经济新常态下我国民航业发展的趋势和对策[J].综合运输, 2015,10(37):7-10.

[2]中国民用航空局.2014年民航行业发展统计公报[N].中国民航报, 2015-07-15(001).

[3]邢志伟,冯文星,罗 谦,等.基于航班离港时刻主导的单航班离港旅客聚集模型[J].电子科技大学学报,2015,44(5):719-724.

[4]PROFILLIDIS V A,BOTZORIS G N.Fuzzy and Time series Models for the Forecast of Transport Demand[C]//Fuzzy Systems Conference IEEE International,2007,7(3):23-26.

[5]BANDEIRA,MICHELLEC G S P.Key indicators that affect the perception of service quality in critical airport areas of passenger boarding [J].J Transp Lit,2014,8(4):7-36.

[6]GCL BEZERRA,CF GOMES.The effects of service quality dimensions and passenger characteristics on passenger’s overall satisfaction with an airport[J].Journal of Air Transport Management,2015,3(1):77-81.

[7]AKDERE M,ETINTEMEL U,TATBUL N.Plan-Based Complex Event DetectionAcrossDistributedSources[C]//VLDB,Auckland,New Zealand, 2008:66-77.

[8]TAHERSIMA H,TAHERSIMA F,SOHANI A M,et al.Prediction of Lorenz Chaotic Time Series via Genetic Algorithm[C]//2010 IEEE International Conference on Computational Intelligence for Measurement Systems and Applications(CIMSA),2010:13-17.

[9]徐定杰,沈 忱,沈 锋,等.混合高斯分布的变分贝叶斯学习参数估计[J].上海交通大学学报,2013,47（7):1119-1125.

[10]熊坤来,刘章孟,柳 征,等.基于EM算法的宽带信号DOA估计及盲分离[J].电子学报,2015,10（10):2028-2033.

[11]张亚平,贾国洋,程绍武,等.基于Petri网的航站楼安检流程建模及性能分析[J].武汉理工大学学报,2015,39(4):688-691,697.

[12]徐 捷,徐从富,耿卫东,等.基于粗糙集理论的动态目标识别及跟踪[J].电子学报,2003,30（4):605-607.

[13]杨朝辉.基于卡方检验的SAR图像道路检测算法[J].计算机工程与设计,2012,5(33):1923-1927.

（责任编辑：刘佩佩）

Single airline passenger arrival model in security area based on GMM

YU Zhijing1,BAO Linlin1，2,LUO Qian2
（1.College of Electronic Information and Automation,CAUC,Tianjin 300300,China; 2.The Second Research Institute,CAAC,Chengdu 610041,China）

GMM（Gaussian mixture distribution model）is used for a certain airline passenger arrival distribution fitting analysis.The extremum clustering method is adopted for the premiere distribution inspection of EM algorithm, parameter solution can be got after several iterations.In experimental part,a real airline check-in output data is adopted for experimental verification.Results show that the fitting precision of Gaussian mixture distribution is 90%or more.Compared with common fitting methods,the fitting precision is improved by more than 15%.Compared with extremum clustering and commonly used K means clustering of chi-square Gaussian mixture distribution model,the extremum clustering model has higher accuracy by about 5%.

single airline;Gaussian mixture distribution;EM algorithm;extremum clustering

V351.17

A

1674－5590（2017）02－0046－05

2016-09-18；

2016-10-30

国家自然科学基金项目（U1333122，U1533203）；国家科技支撑计划（2012BAG04B02）；中央高校基本科研业务费专项（3122014P003）；四川省科技支撑计划项目（2016GZ0068）；成都市战略性新兴产品研发补贴项目（2015-CP01-00158-GX）

于之靖（1963—），男，河北沧州人，教授，博士，研究方向为自动化检测技术、光纤传感技术和计算机视觉测量等.