全方位移动升降机结构静、动态有限元分析

刘 源，张学玲

(1.军事交通学院 研究生管理大队，天津300161； 2.军事交通学院 军事物流系，天津 300161)



全方位移动升降机结构静、动态有限元分析

刘 源1，张学玲2

(1.军事交通学院 研究生管理大队，天津300161； 2.军事交通学院 军事物流系，天津 300161)

为精确计算升降平台的静、动态力学特性，利用有限元方法对设计的升降机框架进行分析。首先根据技术指标建立升降机结构模型，然后基于静、动态振动理论和有限元方法对其进行结构力学性能仿真，并比较铝合金和钢两种材料升降机的力学性能。通过静态和动态有限元计算结果比较得出：钢材料升降机在相同载荷下变形要小于铝合金材料，动态固有频率也要比铝合金升降机稍高，且振动变形量要小很多。

升降机结构；有限元分析；静态计算；动态振动

自行式升降平台作为现代物流中物资仓储环节的重要作业装备之一，广泛应用于后方仓库、机场、港口、码头等场合，可实现在狭小空间运送集装物资和长大物资，以及对大件零部件精确定位与安装、装配维修等应用目的[1-2]。升降机结构为细长方钢结构组装，当受到外界频率激励，如人走动、周围电机低速转动、液压驱动等周期性频率激励后，在升降过程中会摇晃，甚至还可能出现共振，导致升降机结构折断而失效。本文在研制自行式全方位移动升降机的基础上，基于动静态分析理论和有限元方法对升降机静、动态机械性能进行有限元仿真计算，保证在升降过程中和升到最大高度时能够有足够的强度和稳定性。

1 升降机设计指标及结构

升降机设计指标：底盘长2 100 mm，宽1 275 mm，高615 mm；升降机收起总高度1 400 mm；最大举升高度6 000 mm；载质量300 kg；空载最大起升速度48 mm/s，满载最大起升速度35 mm/s；满载工作后受力结构件不得永久变形，超载25%任意方向作业可维持稳定性。根据给定的指标，设计升降机，升起机构采用剪叉式结构，液压控制系统的油泵布置在剪叉结构中部，通过液压系统驱动剪叉式结构升降(如图1所示)。

(a)全方位移动升降机收起结构 (b)剪叉结构升起结构图1 全方位移动升降机

由于升降机结构及质量、尺寸、高度、速度等指标限制，设计的结构需要进行结构性能验证，尤其是静态、动态性能的校核。升降机结构比较复杂，用传统的经验计算精度达不到要求。有限元方法可以对复杂结构进行仿真计算，提供可靠的设计数据。

2 结构静、动态分析理论

2．1 结构静力学理论

在工程上弹性范围内，一般应力超出材料屈服强度，则零件失效。刚度是受外力作用的材料、结构抵抗变形的能力，由结构产生单位变形所需的外力值来度量。对大变形结构零件，变形量超出一定范围，零件会失效[3]。

对于复杂空间结构件受力情况，描述物体一点的应力与应变关系满足广义胡克定律[4-5]：

(1)

式中：E为弹性模量；μ为泊松比；ε为线应变；γ为剪应变；σ为正应力；τ为切应力。

求得各结点应变后，根据几何关系，可得到结构的变形[5]。变形量越大，说明结构刚度越差。

2.2 结构动态力学理论

描述多自由度振动系统的微分方程为[3，6]。

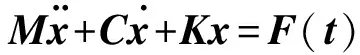
(2)

解上述方程组，即求解系统的运动规律，转化为方程的特征值和特征向量问题。对于无阻尼系统，微分方程为

(3)

设各质点间歇振动，则x=Xcos(ωt-φ)，ω2=λ，代入式(3)，得

(K-λM)X=0

(4)

特征方程为

|K-λM|=0

(5)

X=[X1，…，Xi，…，Xn]

(6)

通过式(3)—式(6)，求得n自由度系统的固有频率和振型。对式(2)所对应的受力系统，同理可求得边界条件下的固有频率和振型，用于了解系统结构特性。

3 升降结构静、动态有限元分析

由上述结构静、动态理论可知，对于简单的结构，可以用传统的估算方法设计。对于类似升降机这种组合的复杂结构，且在应用中有动态力作用，属于多自由度振动范畴，不可能用传统方法计算静、动刚度。为了解所设计的升降机的机械强度和动、静态刚度，在理论基础上，对其进行有限元仿真分析。静态强度和刚度计算主要反映升降机架在工作时的力学强度和静态抗变形能力；动态计算则主要分析升降机在外界激励条件下是否会发生共振变形，避免和结构固有频率接近的频率激励[3]。

3.1 模型和边界条件

为建立有限单元模型，进行力学性质分析，需要在计算时对升降机结构零部件进行必要的简化处理：①不考虑对框架机械性能无影响的液压油管等附件；②去除不影响整体性能的倒角、圆角和远小于整体尺寸的圆孔；③轴销连接简化为固连，由于在升降机工作时，上升到指定位置后机构锁止，此时轴销连接处没有相对运动，因此轴销连接可以简化为固连。轴销和连接件之间的微小间隙有阻尼作用，且阻尼值很小，轻微影响振动衰减的时间，对固有频率、各阶振型和最大振幅的影响可以忽略。此外，连接传力部分做必要的耦合处理，由于升降机模型是单个零件建立并装配而成，各零件之间没有力的传递关系，因此必须进行自由度耦合，才能进行有限元计算。耦合方法为：分别选取两个接触面上在距离容差范围内的节点，设置其6个自由度全相同，即全自由度耦合。简化后的升降机有限元几何模型如图2所示，在Solidworks中建模并装配，在Ansys中进行布尔运算处理[7-8]。

模型单元采用三维壳体单元Shell63，然后给各板厚度按实际值赋值，可减少计算量且保证精度。升降平台材料为铝合金，其力学性能参数为[4]：E=7．0×1010Pa，μ=0．27，ρ=2 700 kg/m3；屈服极限σs=(190～200)MPa。

图2 升降机有限元几何模型

边界条件考虑最严工况——满载条件，对底面和底盘连接部位进行约束，约束位置和方向按照实际情况施加。假设操作者质量为100 kg，位置在升降机伸出远端，货物质量为200 kg，均匀作用在上平台800 mm×400 mm的面积上，则平台所承受质量总共为300 kg。满载时平台边界条件如图3所示。

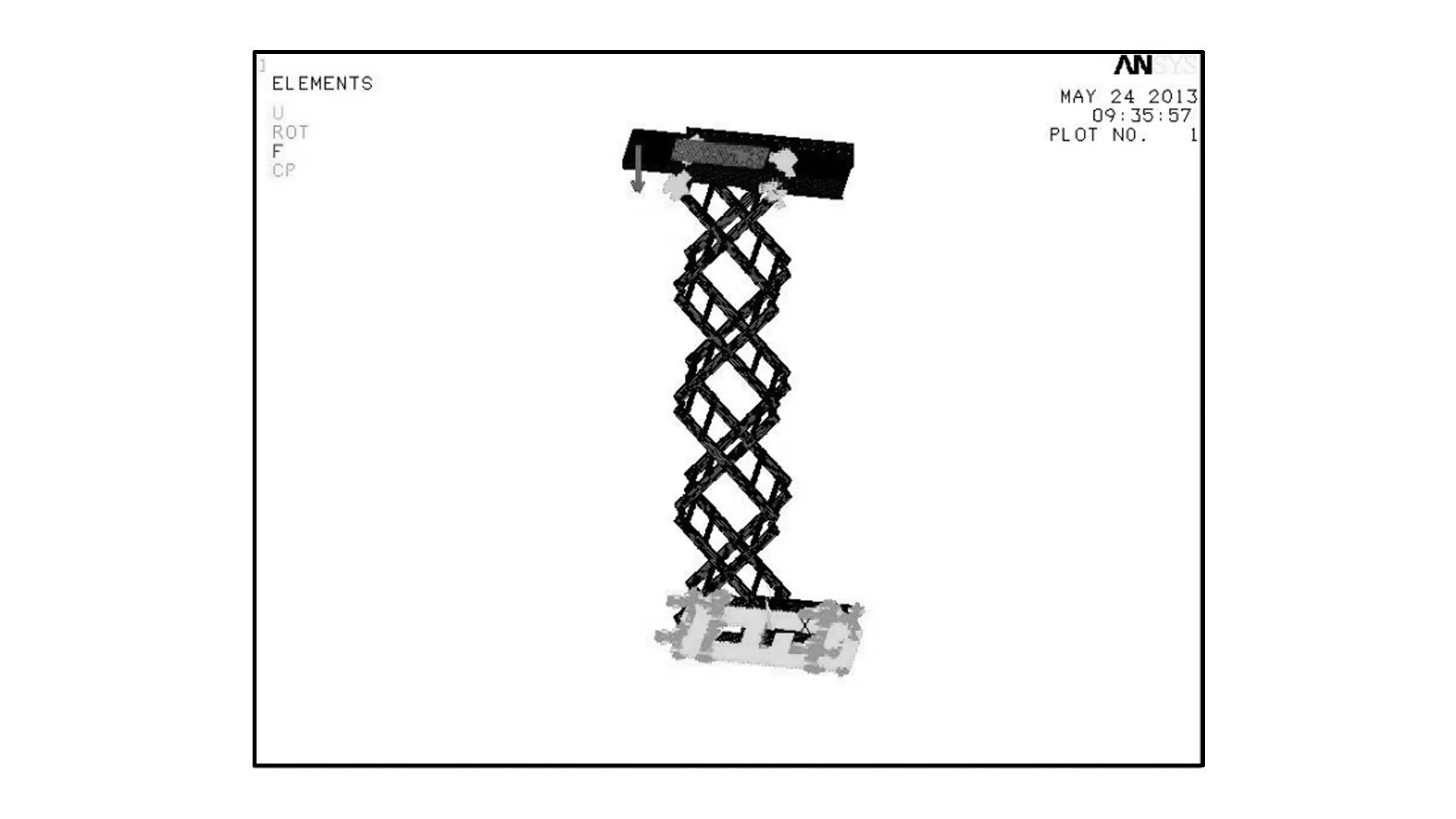
图3 升降机满载时边界条件

3.2 静态计算

以上边界条件下，计算升降平台的应力与变形[7-8]。其静态应力与变形量见表1，其部分应力云图和变形云图如图4、图5所示。

表1 铝合金平台静态应力与变形

从有限元仿真结果可以看出，满载货时最大应力为121 Mpa，小于铝合金材料屈服极限。满载货物300 kg时，最大变形为29.94 mm，由于升降平台升到最高点时，高度最大尺寸为6 000 mm，变形量与总受力高度的比为0.49%，大于许用值0.2%。虽然静态强度满足要求，对于尺寸较大的大变形结构件，会由于变形太大而失效，因而铝合金材料的升降机刚度不满足要求。

(a)整体应力

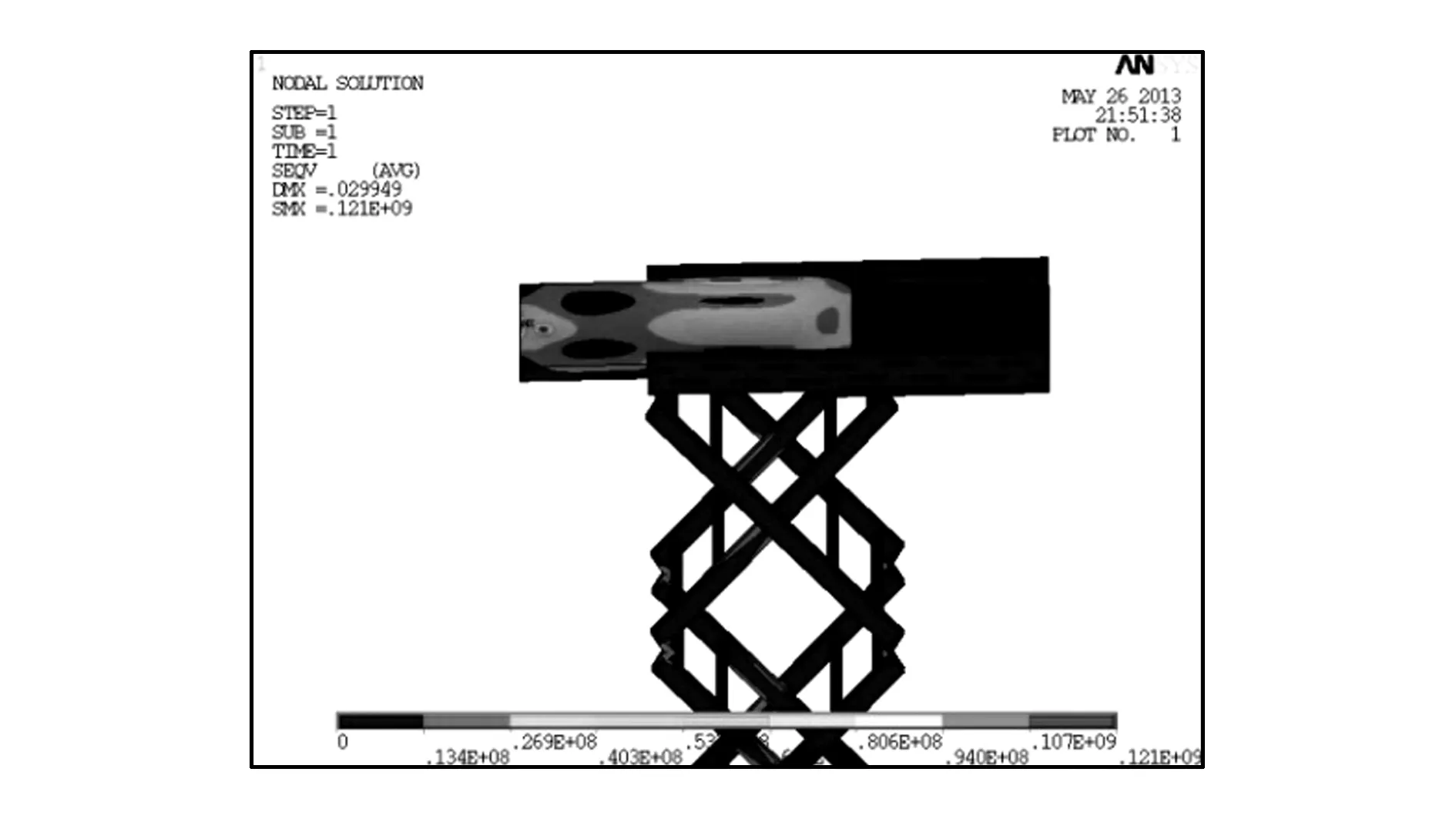
(b)局部应力图4 满载时铝合金升降平台应力云图

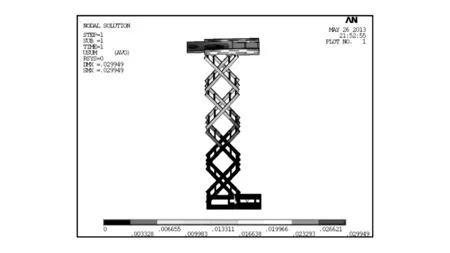
(a)综合变形

(b)X向(左右)变形图5 满载时铝合金升降机变形云图

3.3 动态分析

当升降机起升过程或升到最高时，受到冲击或振动作用，会引起动共振或临界状态失稳，因此需要做升降机起升时的模态分析，了解此时边界条件下的固有频率和振型，避免动态振动失效。将底面与底盘固定点约束，假设人站在最远端，进行有限元模态分析[7-8]。平台固有频率和该频率下变形量见表2，模态前6阶振型如图6所示。

表2 铝合金和钢升降机模态频率及动变形量比较

由动态计算结果(见表2中部分数据和图6)可知：升降平台升起后，前2阶固有频率较低，当平台升起后，受到接近其固有频率的外力作用时，会有相应的动变形量；持续的外力作用甚至会出现共振而损坏。因此，应当避免以接近固有频率的外力激励(如操作者在平台上频繁走动)作用在升降平台上。

3.4 升降机材料改进后结构比较

由以上铝合金材料的升降机结构静态和动态仿真计算可知，如果采用铝合金材料，成本较低，质量减轻，但结构刚度差，不能满足要求。因此，采用碳钢作为升降机材料，进行相同条件下机械结构静、动态性能计算，并进行比较。

钢材料力学性能参数[4]为：E=2．06×1011Pa，μ=0．27，ρ=7 800 kg/m3，σs=(350～500)MPa。通过静态和动态计算，钢升降机平台满载时静态受力情况下应力与变形云图如图7、图8所示。

由图7、图8可知：钢升降平台相同条件下最大应力126 MPa，小于钢材料屈服极限；最大静变形11.03 mm，变形量与最大变形尺寸比值11.03/6 000=0.183%,小于许用值0.2%，因而满足要求。

铝合金和钢平台的静态应力与变形量比较见表3。可见，各方向及综合变形均小于铝合金材料，为铝合金升降机变形量的37%～49.6%之间，刚度大大提高。钢升降机动态计算结果和铝合金升降机比较见表2。钢结构升降机的固有频率和铝合金升降机相近，但对应频率下的变形值要小得多。

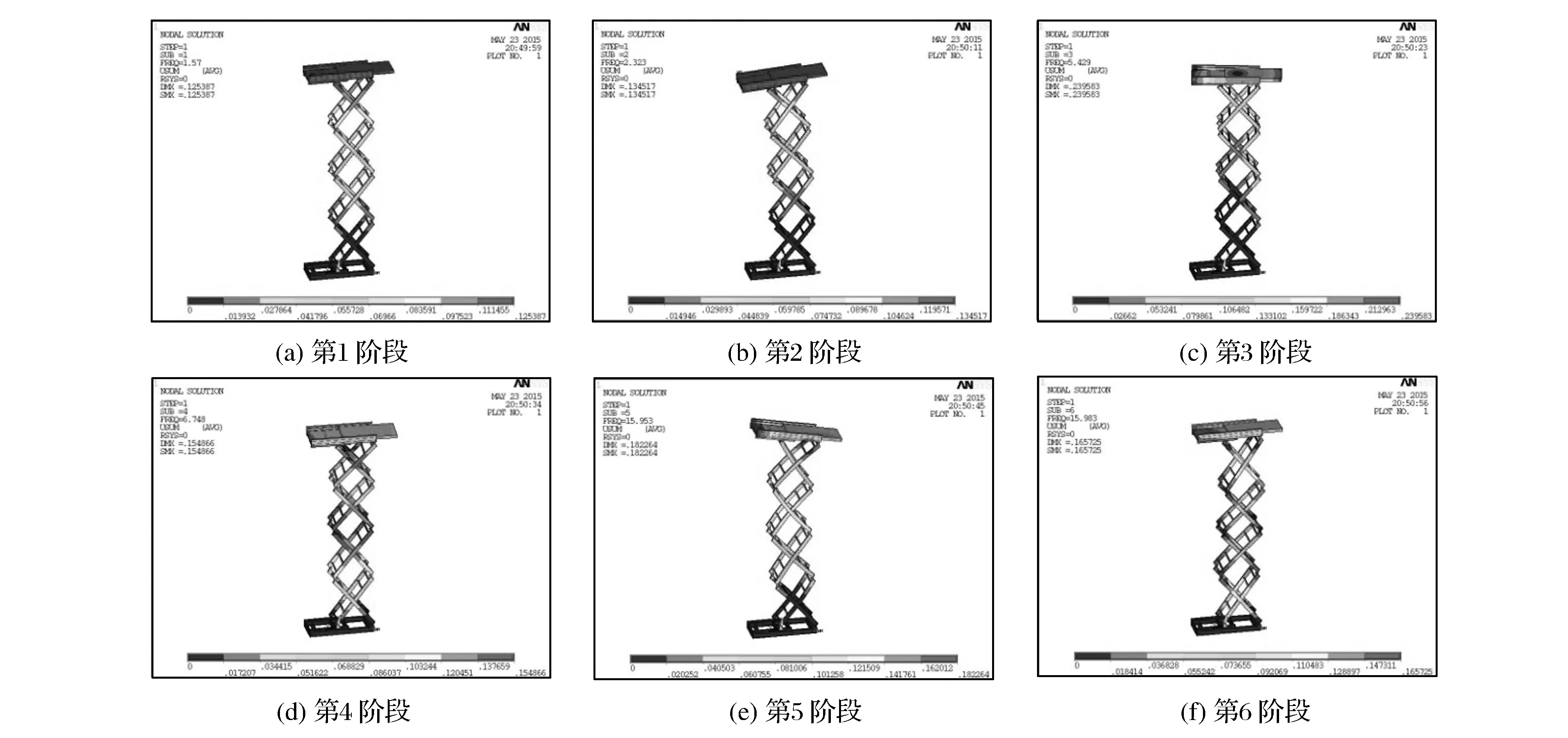
图6 铝合金升降机前6阶模态振型

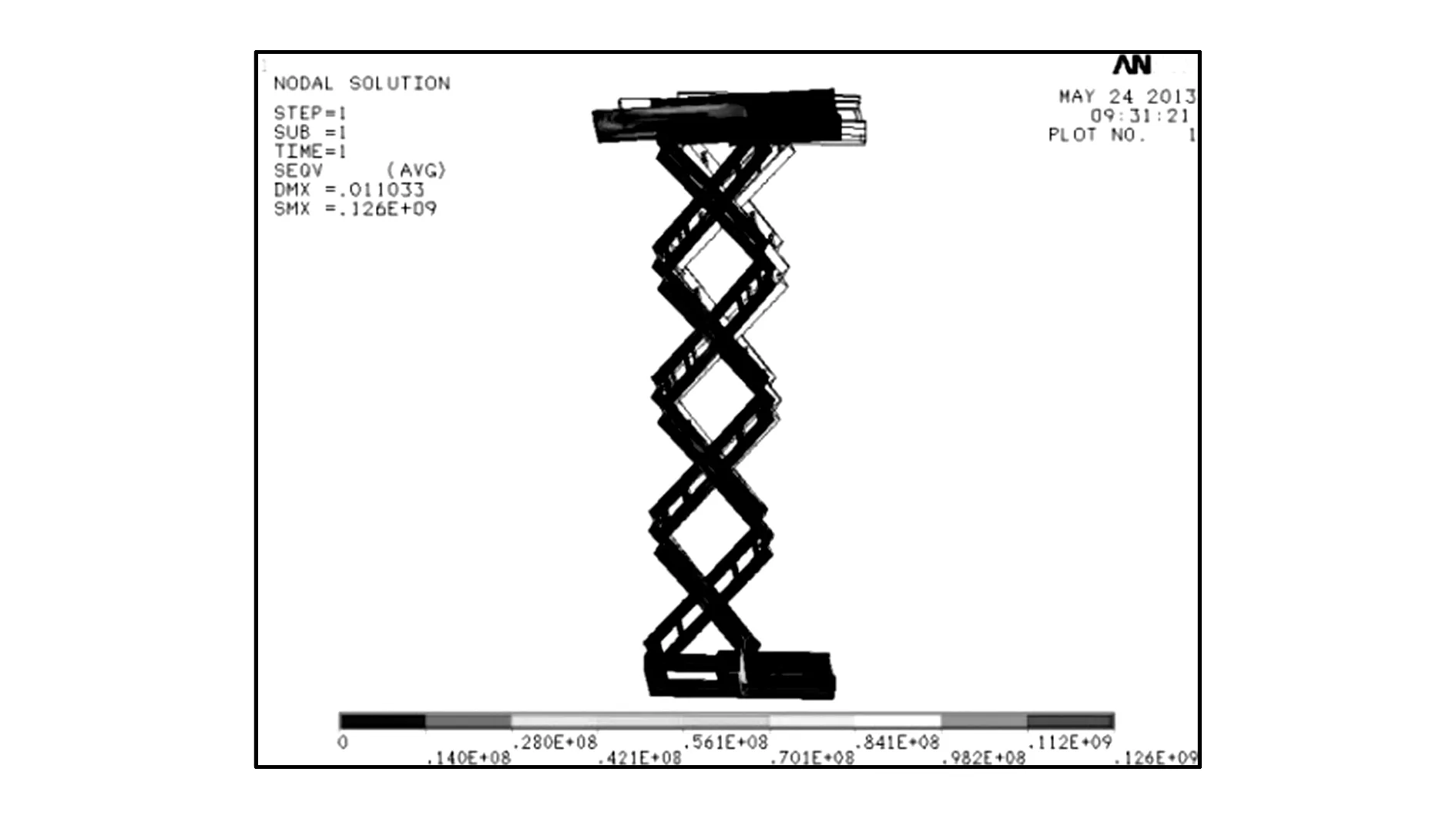
(a)整体应力

(b)局部应力图7 满载时钢升降机应力云图

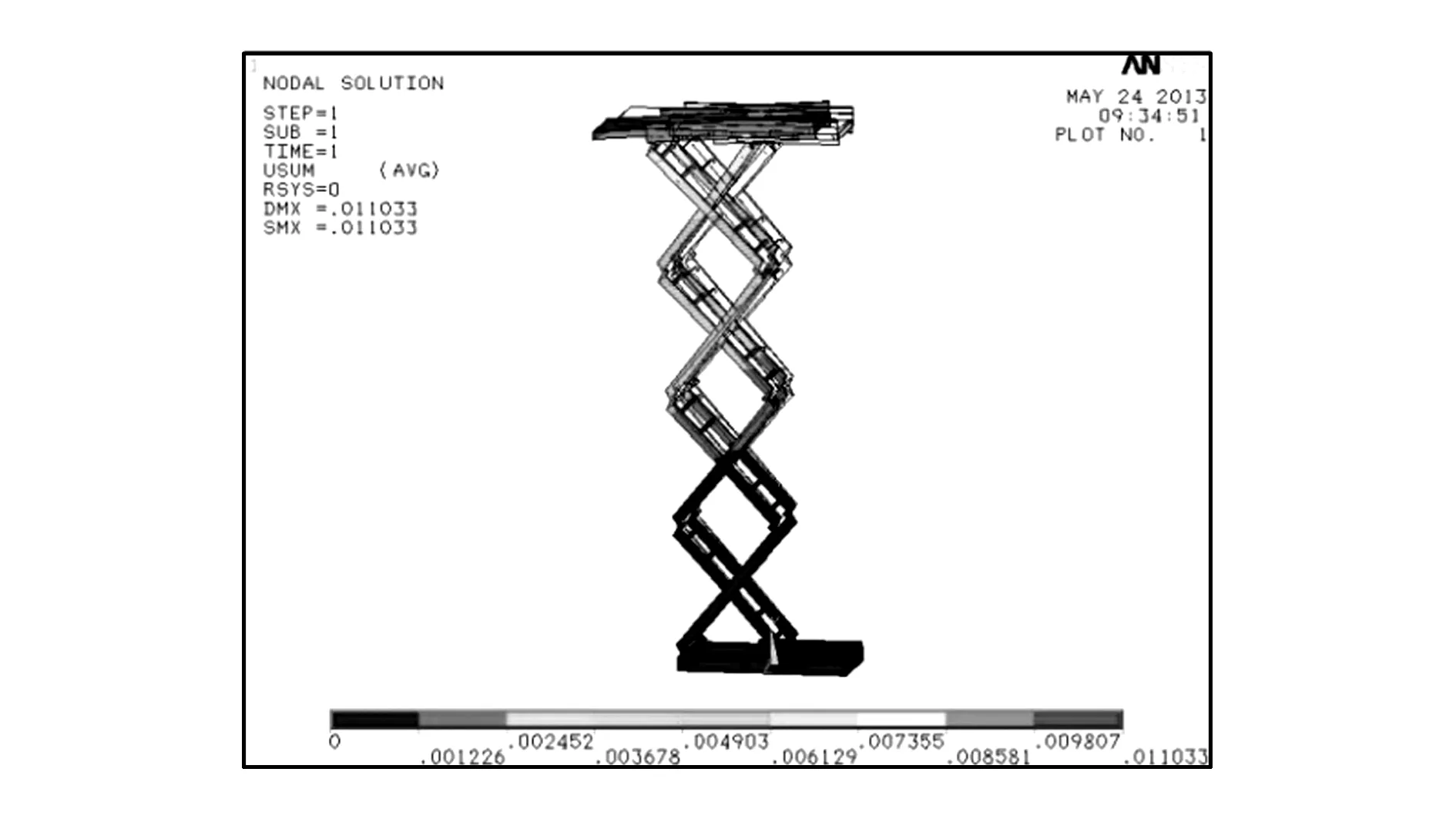
(a)综合变形

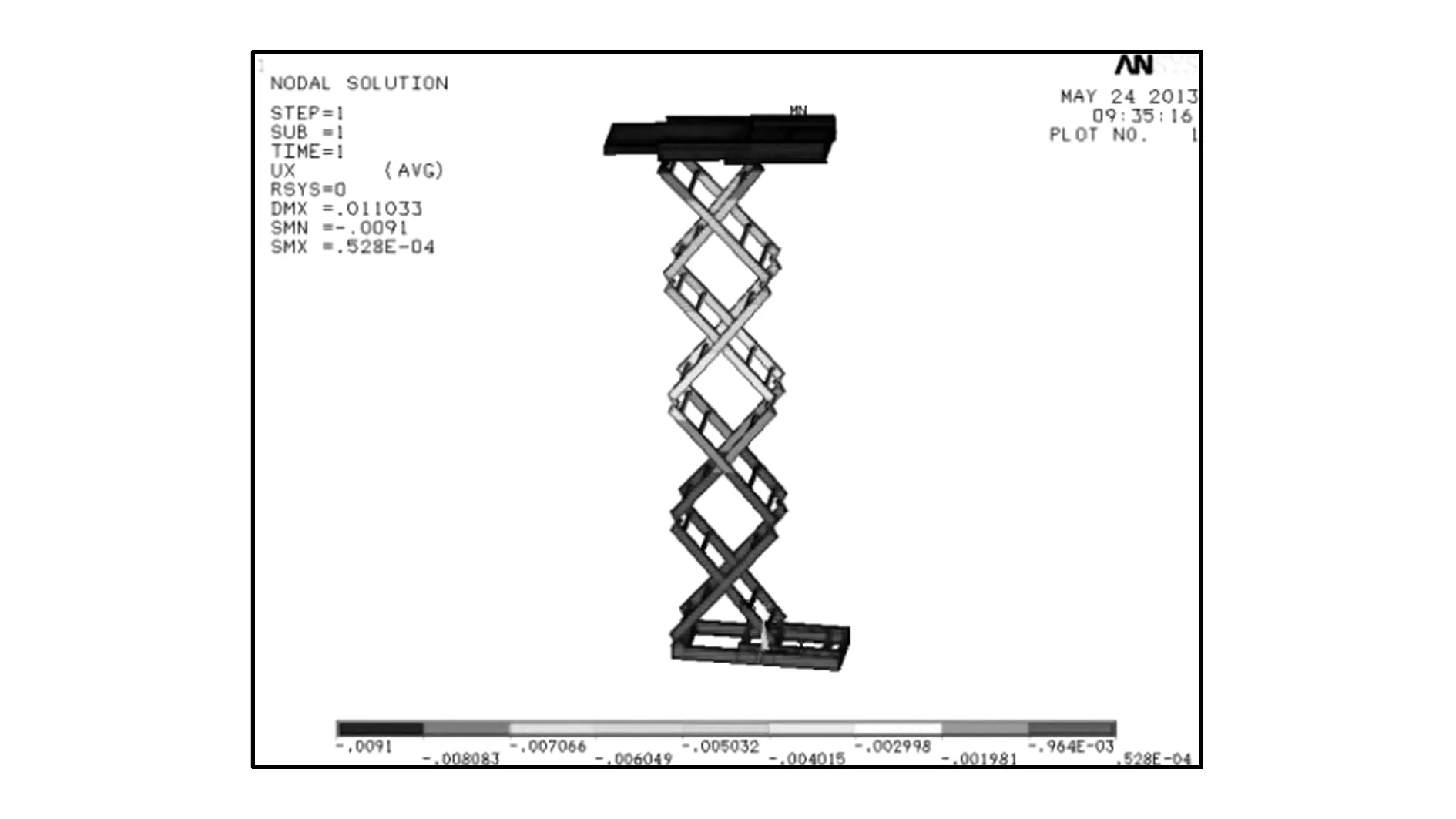
(b)X向(左右)变形图8 满载时钢升降平台变形云图

升降机材料应力/MPa变形量/mmX向(左右)Y向(上下)Z向(前后)综合铝合金12123．2213．080．2729．94钢 1269．106．490．1411．03

通过静态和动态有限元计算结果比较可以看出：钢材料升降机在相同载荷下变形要小于铝合金材料，动态固有频率也要比铝合金升降机稍高，且振动变形量要小很多。因此，设计采用钢材料的升降机。图9为本文设计的升降机样机。升降机升到最高位置时的第1、2阶固有频率分别为1.58 Hz和2.34 Hz，频率值较低，与人走路的频率接近，应当避免在平台上频繁走动而引起结构共振。

图9 钢结构升降机样机

4 结 语

对于单向尺寸较大的结构件，静、动刚度和稳定性至关重要，而由于结构复杂，其力学性能不能通过估算得出。本文通过对升降机结构建模并基于静、动态振动理论和有限元方法的仿真，精确计算出升降机框架结构的静、动态力学特性，使结构、材料设计满足要求，且为升降机的正常操作使用提供指导。本文设计改进的升降机已经投入生产。

[1] 邵长鹏．浅谈仓储物流的现状和可持续发展[J]．经济技术协作信息，2009(19)：120.

[2] 苗云飞．我国仓储物流业发展现状及趋势[J]．铁路采购与物流，2009(8)：56.

[3] 闻邦椿.机械振动理论及应用[M]．北京：高等教育出版社，2009：33-34．

[4] 成大先. 机械设计手册：第1卷[M]．5版.北京：化工工业出版社，2008：118．

[5] 王勖成.有限单元法[M]. 北京：清华大学出版社，2003：176-180.

[6] 刘延柱，潘振宽，戈新生．多体系统动力学[M]．2版.北京：高等教育出版社，2012：196-199．

[7] 王新敏．ANSYS结构动力分析与应用[M]．北京：人民交通出版社，2014：156-157．

[8] 胡仁喜，康士廷．ANSYS14.0机械与结构有限元分析从入门到精通[M]．北京：机械工业出版社，2013：217．

(编辑：史海英)

Static and Dynamic Finite Element Analysis of Omni-directional Mobile Lifter Structure

LIU Yuan1, ZHANG Xueling2

(1.Postgraduate Training Brigade, Military Transportation University, Tianjin 300161, China; 2.Military Logistics Department, Military Transportation University, Tianjin 300161, China)

To calculate the static and dynamic mechanical characteristics accurately, the paper analyzes the lifter framework with finite element method(FEM). Firstly, it establishes lifter structure model according to the technical indicators. Then, it simulates the mechanical characteristics with static and dynamic vibration theory and FEM, and compares mechanical characteristics of lifters with aluminum alloy and steel. The calculation result with static and dynamic finite element shows that the deformation of steel lifter is smaller than that of aluminum alloy lifter under the same load, and its dynamic natural frequency is higher than aluminum alloy lifter but vibration deformation is much smaller.

lifter structure; finite element analysis; static calculation; dynamic vibration

2016-07-12；

2016-10-28．

天津市科技支撑计划项目(12ZCZDGX02200).

刘 源(1993—)，男，硕士研究生； 张学玲(1970—)，女，博士，副教授，硕士研究生导师.

10．16807/j.cnki.12-1372/e.2017.05.019

TH114

A

1674-2192(2017)05- 0082- 06

● 基础科学与技术 Basic Science & Technology