一种基于神经网络的自适应非线性自动舵

武慧勇，唐匀龙

(1.中国电子科技集团公司第三十八研究所，安徽 合肥 230088；2.孔径阵列与空间探测安徽省重点实验室，安徽 合肥 230088)



一种基于神经网络的自适应非线性自动舵

武慧勇1,2，唐匀龙1,2

(1.中国电子科技集团公司第三十八研究所，安徽 合肥 230088；2.孔径阵列与空间探测安徽省重点实验室，安徽 合肥 230088)

针对仅航向角可测量的船舶航向控制系统，提出一种基于神经网络的自适应非线性航向控制器。首先采用神经网络在线逼近系统中的未知项，并设计滑模观测器在线估计艏摇角速度；然后基于动态面控制思想设计非线性观测器-控制器。利用Lyapunov方法证明了误差变量是一致最终有界的。以某自航船模为例仿真，结果表明所提方法鲁棒性好，且操舵合理。

航向控制器；非线性；神经网络；观测器-控制器；动态面控制

0 引 言

随着世界航运业的迅速发展，船舶航向控制一直受到广泛的关注[1-2]。工程上常用的航向控制方法是比例积分微分(PID)控制，但由于船舶操纵过程具有的大惯性、非线性等特性，会使船舶围绕期望航线呈周期性偏航运动[1]，从而造成过多的操舵，在存在海浪干扰的情况下，偏航效果更明显。为提高控制精度，减少偏航，需采用一些先进的控制方法，目前用于船舶运动控制的方法主要有：鲁棒控制[3-4]、自适应控制[5]、滑模控制[6]、反步法[7-8]以及基于人工智能的控制方法[9-10]等。其中反步法因其方便构造Lyapunov函数而受到广泛关注。为了解决反步法对虚拟控制律重复求导的问题，文献[14]通过引入一阶滤波器而避免了对虚拟控制律的直接求导，简化了控制器设计。文献[17]则是通过引入二阶滤波器避免数值求导。文献[8]采用的动态面(DSC)思想同样是通过引入滤波器避免对虚拟控制律直接求导。可见通过引入滤波器可较好地解决反步法中对虚拟控制律重复求导的问题。

神经网络是估计系统中未知项的有效工具，常用的有径向基(RBF)神经网络[6]、单隐层神经网络[10]等。但是RBF网络和单隐层神经网络是静态网络，输入节点较多，且易受噪声影响。而动态递归模糊神经网络(DRFNN)同时具有递归神经网络和模糊逻辑的优点，它内部包含一个反馈回路，从而可更好地反映系统的动态映射关系[11]。且由于存在内部反馈回路，对于存在微分关系的输入变量，无需全部作为DRFNN网络的输入，从而简化了网络的结构，加快了学习速度。

在船舶航行过程中，艏摇角速度受环境干扰的影响较大，有时甚至不可直接测量，因此有必要设计状态观测器。文献[10]采用一种单隐层神经网络近似估计航向控制系统中的未知非线性函数，并设计观测器为神经网络权值更新提供自适应信号，最终设计了船舶航向自适应鲁棒控制器。文献[12]针对航向控制问题，提出了可独立设计的滑模观测器和反步控制器，但文中需要已知干扰和建模误差的上界，而这在实际系统中通常很难确定。

本文针对艏摇角速度不可测量的船舶航向跟踪控制系统，考虑建模误差及外部干扰，提出了一种基于动态递归模糊神经网络的非线性观测控制器。首先基于神经网络设计了二阶滑模观测器，然后基于动态面控制的思想，利用状态估计值设计了非线性观测控制器，并根据Lyapunov定理证明了误差的一致有界性。仿真表明，本文方法可使船舶快速准确地跟踪期望航向，且对模型不确定和外部干扰具有良好的鲁棒性。

1 问题描述

考虑模型不确定性，船舶航向控制系统的非线性数学模型为[3]：

(1)

本文设计控制器时考虑舵机系统的特性，船舶舵机特性常用下列模型表示：

(2)

式中：δR为命令舵角，也是本文所设计的控制律；KR为舵机控制增益；TR为舵机时间常数。

定义状态变量x1=ψ，x2=r，x3=Kδ/T，控制变量u=δR，则由式(1)、式(2)可将船舶航向控制系统的非线性数学模型表示为：

(3)

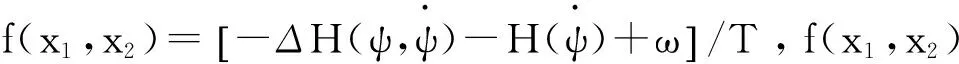
控制目标：对于非线性系统(式(3))，设计控制律u，消除复合干扰的影响，且使x1能稳定跟踪期望航向ψd。

2 基于神经网络的观测器设计

由于艏摇角速度x2的测量受风、浪、流等环境干扰的影响较大，本文将设计二阶滑模观测器对其进行观测。同时对于复合干扰f(x1,x2)，本文将采用动态递归模糊神经网络进行在线逼近。

2.1 动态递归模糊神经网络

(4)

式中：cij和bij分别为高斯函数的中心和基宽。

第3层为规则层，每个节点代表1条规则，模糊推理运算在这一层进行。同时第3层包含1个内反馈回路，可用来捕获系统的动态响应而不必在外部添加延时反馈环节。第3层的输出为：

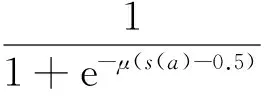
(5)

式中：a=1,…,m；j=1,…,m，m为规则数，且：

(6)

αc,j(k)=αj(k-1)

(7)

(8)

第4层为状态层，其输出为第3层推理结果的线性组合，本文取归一化方式，即：

(9)

由图1可知，最后一层为第4层输出的加权和：

(10)

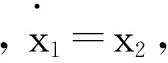
定义神经网络的参数向量为：

(11)

式中：w和φ分别为第3层和最后一层的权值参数。

根据神经网络逼近理论可知，存在理想的参数向量θ*，使动态递归模糊神经网络以精度ε逼近未知函数f(x1,x2)，即：

(12)

因此可知f(x1,x2)的神经网络的估计值为：

(13)

根据式(12)和(13)，并应用泰勒展开，可得神经网络的估计误差为：

(14)

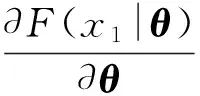
2.2 二阶滑模观测器

在实际中，舵角x3比较容易测量，而艏摇角速度x2受环境干扰的影响较大，不可直接测量。因此本文设计观测器如下：

(15)

式中：v1,v2为观测器输入，分别为[13]：

(16)

式中：σ1,σ2均为正数；sign(·)为符号函数。

由式(3)、(15)和(16)可得，观测器误差方程为：

(17)

根据式(15)～(17)即可估计出x2。

设计动态递归模糊神经网络参数向量的自适应律为：

(18)

式中：γ>0；Γ为正定矩阵。

3 基于观测器的航向控制器设计

3.1 航向参考模型

(19)

式中：ψr为指令航向阶跃输入；ζ和ωn为滤波器参数；滤波器输出ψd为控制系统的参考信号。

3.2 控制器设计

(20)

(21)

为避免下一步中直接对α1求导，使用一阶低通滤波器对其进行滤波[15]，滤波器模型如下：

(22)

(23)

则将式(23)代入式(21)，得：

(24)

(2) 定义误差变量z3=x3-α2，选取Lyapunov函数为V2=V1+0.5s2，两边求导得：

(25)

设计如下滤波器对虚拟控制律进行滤波：

(26)

(27)

则将上式代入式(25)得：

(28)

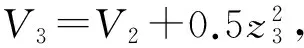
(29)

根据式(29)，设计控制律为：

(30)

4 稳定性分析

(31)

对式(31)两边求导可得：

(32)

根据式(22)和(26)可得：

(33)

(34)

将式(14)、(18)、(29)、(33)、(34)代入式(32)得：

(35)

根据文献[16]中的引理4.3知，存在κ∞类函数κ11,κ12和κ22,κ22使得式(36)对任意xi∈Rn(i=1,2,3)成立

(36)

对式(35)中耦合项进行不等式放缩得

(37)

(38)

(39)

(40)

(41)

(42)

(43)

将式(37)～(43)代入式(35)得:

(44)

其中:

(45)

(46)

解不等式(46)可得：

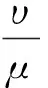
(47)

要注意，滤波器(22)和(26)中的滤波时间常数τ1,τ2对系统性能影响较大，一般情况下，可取值0.01～0.03，此时效果较好[14]。

定理1：针对系统(3)，设计观测器动态方程(15)，采用控制律(30)、观测器输入(16)、神经网络参数向量自适应律(18)，那么选择合适的参数σ1,σ2,k1,k2,k3,Γ,γ,可使闭环系统中所有误差信号一致最终有界。

5 仿真验证

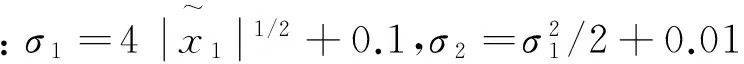
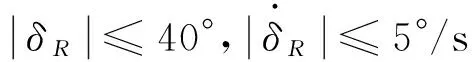
在存在模型不确定及外部干扰时，从图2可以看出，PID控制无法满足跟踪要求，而本文方法精度高、响应快且鲁棒性好；图3和图4比较了本文方法和未加神经网络补偿的算法。可以看出，未加神经网络补偿时，航向跟踪误差出现震荡，误差收敛域变大；舵角变化较频繁，变化幅度较大，且有抖振，这将对船舶舵机的寿命及能耗带来不利的影响，而本文方法控制舵角光滑且操舵合理，对于实际应用具有重要意义。

图5和图6分别为采用本文方法的观测误差变化和观测器输入曲线，图7为未加神经网络补偿时的观测误差曲线。可以看出，未加神经网络补偿时，观测误差明显变大，这也是导致航向跟踪误差变大的主要原因。

6 结束语

针对艏摇角速度不可直接测量的船舶航向跟踪控制系统，考虑模型不确定及未知外部干扰，提出了一种基于神经网络的非线性观测控制器。闭环系统中考虑了舵机响应模型，与实际系统更相符。采用动态递归模糊神经网络在线估计系统中未知项，并设计了二阶滑模观测器对艏摇角速度进行观测，且设计观测器参数时，无需已知外部干扰和模型不确定性的上界。然后基于动态面控制的思想，设计了非线性观测控制器。通过Lyapunov定理，证明了闭环系统所有误差信号一致最终有界。仿真表明所提方法对于模型不确定和外部干扰具有良好的鲁棒性，可使观测误差和跟踪误差快速收敛，且操舵响应良好，对实际应用具有重要意义。

[1] 张桂臣,任光.不依靠模型自适应控制的船舶自动舵[J].船舶工程,2008,30(1):37-40.

[2] 郑云峰,杨盐生,李铁山.带有执行机构的船舶航向控制反馈线性化设计[J].大连海事大学学报,2004,30(3):14-17.

[3] 罗伟林,邹早建,李铁山.船舶航向非线性系统鲁棒跟踪控制[J].控制理论与应用,2009,26(8):893-895.

[4]ZHANGXK,WANGXP.Concisenonlinearrobustcontrolofcoursekeepingforships[J].ICICExpressLeters,2010,4(4):1263-1267.

[5]KAHVECINE,IOANNOUPA.Adaptivesteeringcontrolforuncertainshipdynamicsandstabilityanalysis[J].Automatica,2013,49(3):685-697.

[6] 肖海荣，李贻斌，周凤余，韩耀振.基于径向基函数网络调节的船舶航向非线性系统滑模控制[J].中南大学学报(自然科学版),2011,42(S1):17-22.

[7]WITKOWSKAA,TOMERAM,SMIERZCHALSKIR.Abacksteppingapproachtoshipcoursecontrol[J].Int.J.Appl.Math.Comput.Sci.,2007,17(1):73-85.

[8] 刘程,李铁山,陈纳新.带有舵机特性的船舶航向自动舵DSC-MLP设计[J].哈尔滨工程大学学报，2012,33(1):1-6.

[9]HUGS,ZHOUYB,XIAOHR.Applicationoffuzzyneuralnetworkinshipcoursecontrol[C]//AppliedMechanicsandMaterials,2012:309-315.

[10]王志文，彭秀艳.基于自适应输出反馈的船舶航向控制[J].北京理工大学学报，2011,31(4):425-429.

[11]张平均，蒋新华.基于动态递归模糊神经网络的共振频率自适应反推控制[J].信息与控制，2011,40(1):21-25.

[12]朱齐丹，周芳，赵国良，包卫卫.基于反步法和滑模观测器的船舶航向控制[J].华中科技大学学报(自然科学版)，2009，37(4):122-125.

[13]NOLLETF,FLOQUETT,PERRUQUETTIW.Observer-basedsecondorderslidingmodelawsforsteppermotors[J].ControlEngineeringPractice,2008,16(4):429-443.

[14]DUJ,GUOC.Nonlinearadaptivedesignforcourse-trackingcontrolofshipwithoutaprioriknowledgeofcontrolgain[J].ControlTheory&Application,2005,22(2):315-320.

[15]SWAROOPD,HEDRICKJK,YIPPP,GERDESJC.Dynamicsurfacecontrolforaclassofnonlinearsystems[J].IEEETransactiononAutomaticControl,2000,45(10):1893-1899.

[16]KHALILHK.NonlinearSystems[M].ThirdEdition.UpperSaddleRiver,NewJersey:Prentice-Hall,2002:145-146.

[17]FARRELLJA,POLYCARPOUM,SHARMAMetal.Commandfilteredbackstepping[C] // 2008AmericanControlConference.Washington,USA,2008:1923-1928.

A Nonlinear Adaptive Autopilot Based on Neural Network

WU Hui-yong1,2,TANG Yun-long1,2

(1.No.38 Research Institute,China Electronic Technology Group Corporation,Hefei 230088,China; 2.Key Lab of Aperture Array and Space Application,Hefei 230088,China)

Aiming at ship course control system in which only the course angle can be measured,this paper proposes a nonlinear adaptive course controller based on neural network.Firstly the neural network is used to online approach the unknown terms in the system,and a sliding mode observer is designed to estimate the yaw angular velocity online;then a nonlinear observer-controller based on the dynamic surface control idea is designed.According to the Lyapunov approach,all the error variables are proved to be uniformly ultimately bounded.Finally,simulation of a self-propelled ship model is performed,and the result demonstrates that the designed controller has good robustness and the steering gear operation is reasonable.

course controller;nonlinear;neural network;observer-controller;dynamic surface control

2016-11-09

TP273

A

CN32-1413(2017)02-0092-07

10.16426/j.cnki.jcdzdk.2017.02.022