基于分形理论的通信对抗技术研究
2017-06-05彭小名游敬云
彭小名,游敬云,2
(1.中国电子科技集团公司第三十六研究所,浙江 嘉兴 314033;(2.通信信息控制和安全技术重点实验室,浙江 嘉兴 314033)
基于分形理论的通信对抗技术研究
彭小名1,游敬云1,2
(1.中国电子科技集团公司第三十六研究所,浙江 嘉兴 314033;(2.通信信息控制和安全技术重点实验室,浙江 嘉兴 314033)
基于分形理论和分形特性,从突发信号检测和分形滤波2个方面,研究了分形理论在通信侦察中的应用,并针对通信信号的发射和接收特性,利用分形的自相似等特性,提出了分形信号干扰技术,并从时、频和瞬态等方面初步分析了可行性,从而为通信对抗开启了一扇新的大门。
分形;通信对抗;信号检测
0 引 言
通信对抗作为现代高技术信息化战争的重要组成部分,经过几十年的发展,已取得了长足的进步[1]。然而,通信技术的发展也是日新月异,通信新技术、新体制如雨后春笋不断涌现,如:混沌通信、量子通信、隐蔽通信等,各种抗干扰手段越来越多,如抗低截获概率、猝发通信等,另外战场电磁环境复杂多变,突出表现在通信信号瞬息万变,且呈现信号密集、动态范围大、带宽宽窄各异、调制方式千差万别等技术特征[2-3],使得基于线性、平稳体制的通信侦察技术面临前所未有的挑战,传统的以噪声调频为主的压制干扰理论和方法已显出疲态。因此迫切需要创新性提出、研究在复杂瞬变、耦合约束态的通信侦察新机理、新方法,探索、寻求能够大大降低干扰功率的新的干扰理论、干扰体制和干扰技术,以支撑未来信息化装备的研制和开发。
分形作为一门非线性的边缘学科,具有自相似和无标度等新特性,可以有效地对信号的瞬态特性进行分析和对信号耦合微分方程解耦,为非合作信号的侦收、检测、识别和提取提供新技术,且可有效规避传统的信号处理算法,为通信对抗注入新活力,因而为通信对抗的新思路、新方法研究带来了曙光。
自从1919年,Hausdorff引入分形的概念,随后经Besicovitch和Mandelbort进行了改进和发展,使分形思想具体化、系统化和科学化,Mandelbort的开创性著作《自然界的分形几何》的发表,标志着分形理论的形成。由于分形理论不仅在理论上而且在使用上都具有重要价值,因此很快引起了许多学科的关注,并得到快速的发展。通信信号发射、传输和接收中呈现的非线性、随机性、瞬态等不规则特性导致通信侦察系统无法进行有效的侦收、检测和识别,而分形对不规则图形、现象和过程的描述,具有天然的优势。目前,利用分形已广泛应用到信号识别、天线设计、信号压缩编码、信号滤波、信号检测等方面[4]。吕铁军利用分形理论从信号中提取盒维数和信息维数作为识别特征,对连续波(CW)、二进制频移键控(BFSK)、正交频移键控(QFSK)、二进制相移键控(BPSK)、正交相移键控(QPSK)进行了识别[5]。刘英等设计了分形低剖面天线[6],胡刚等研究了CDMA2000中基于分形滤波的信道估计方法[7]。
本文基于分形理论,利用分形的自相似和无标度等特性,开展非协作信号侦察技术和非线性干扰技术研究,为通信对抗开辟一条新途径。
1 分形及特性
分形是一类复杂性颇高的、没有特征长度,但具有一定意思下自相似的图形和结构的总称。图1和图2为典型的分形图形。
Koch 曲线生成过程为:一条线段作为初始状态(初始态),这条线段替换成4条小线段得到一级生成态;一级生成态的每条线段替换成4条小线段得到二阶生成态,通过无限反复迭代,得到Koch分形曲线,如图1所示。
Mandelbrot分形数学模型非常简单,它描述了复平面上关于复数参数C的一维二次方程z=zα+C的迭代情况,如图2所示。
通过上述图形发现,分形在多处呈现处处不可导性,同时还具有2个典型的基本特性:自相似性和标度不变性。
1.1 自相似性
自相似性是指局部(部分)与整体或另一局部在形态、功能、信息等方面具有某种意义下的相似性,适当地放大或缩小分形对象的几何尺寸,整个结构并不改变。需要指出的是,通常所说的自相似可以分为两类:一类是完全相似,它们一般由数学模型生成,具有严格的自相似性,这类分形通常称为规则分形;另外一类就是统计相似性,其相似性并不是严格的,只有在一定的标度内存在,这类分形通常称为随机分形。自然界中的分形大部分属于随机分形。
1.2 标度不变性
标度不变性是分形集所固有的特性。所谓标度不变性是指无论测量尺度如何改变,所测量对象的特性(如形态特性、复杂程度、不规则性、统计特性等)均不发生变化。当然,除了严格的数学模型外(例如:Koch曲线),对于实际的分形集来说,这种标度不变性只在一定的范围内适用。通常把标度不变性适用的空间称之为该分形体的无标度区间,也就是自相似性存在的区间。而无标度区间的范围通常是以具体研究对象的性质而定。此外分形还具有以下特性:
(1) 分形具有精细的结构,即任意小比例尺度内包含了整体,类似于生物中的全息率。
(2) 分形具有不规则性,以至于它的整体和局部都不能用传统的几何语言来描述。
(3) 在大多数情况下,分形可以以非常简单的方法定义,可以由迭代产生。
(4) 分形在某种方式下定义的“分形维数”通常大于它的拓扑维数。
分形维数的定义多种多样,常见的有Hausdorff维数、盒维数、信息维数、关联维数、广义维数等。实际的分形维数计算方法与所采用的分形模型及具体应用有关。下面主要介绍Hausdorff维数。
设F为Rn中的一个子集,s为一个非负数,对任何δ>0,定义:
(1)
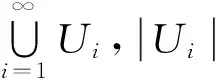
(2)
对于集合F,Hs(F)是s的函数,并满足如下特性:若0 随着非线性技术的不断发展,特别是分形理论的不断深入和完善,将分形理论应用于侦察技术,必将提高对具有奇异特性的突发信号(跳频信号、猝发信号)的检测能力,提升滤波参量的自适应性,实现设备的小型化,加强侦察装备适应复杂多变战场电磁环境的能力。 2.1 突发信号检测技术 跳频信号具有抗干扰能力强等特点,被广泛应用到军事通信中。跳频通信具有频域突变特性,即信号具有频域奇异性。猝发信号具有时域突变特性。傅里叶变换是研究函数奇异性的主要工具,其方法是研究函数在傅氏变换域的衰减速度,以推断此函数是否具有奇异性及奇异性大小。但是,由于傅里叶变换缺乏空间局部性,它只能确定一个函数奇异性的整体性质,而难以确定奇异点在空间的位置及分布情况。小波变换具有空间局部化性质。随着小波理论的发展,小波分析也被用于奇异信号检测,小波分析在时域和频域上同时具有良好的局部化性质,能同时获得时域和频域的信息,是一种较好的奇异信号检测方法,但不合适的小波基函数可能大大降低检测效果。而用分形维数DH(F)来检测频谱信号具有随时间变化的特性,它能有效地检测到信号的动态变化,能同时提供短时信号分形维数的值和时域信息,能精确地确定奇异点(跳频点)的发生、恢复时刻,因此可利用分数维开展突发信号检测。 2.2 分形滤波技术[7] 侦察到的信号都是信号和噪声的叠加,即: x(t)=s(t)+n(t) (3) 传统上采用自回归技术进行滤波处理,即: yi=axj+(1-a)yj-1 (4) 理论分析和计算机仿真实验表明这种简单的自回归滤波器有以下特点:(1)a越小,去噪能力越强,但输出幅值变小,相位滞后增大,波形畸变增大;(2)a越大,去噪能力越弱,但幅值和相位变化小,波形保持性好,即信号失真小,输出的实时性好。而在侦察时,所处的电磁环境复杂多变,突出表现在:通信信号频段宽、多制式、大地域、动态分布、调制方式复杂、信号密度高,甚至还有大功率的信号干扰。而自回归技术能够适应噪声较严重情况下的小值a,将对噪声水平较低的信号有过多的、不必要的失真;而适合小噪声下的大值a,滤波器又不能将信号中包含的较强干扰噪声很好地滤除,也就是说固定的控制参数a不能适应不同噪声水平的信号滤波。 分形滤波可以采用先计算信号曲线的分维数DH(F),而使a成为依赖于DH(F)函数的方法,这样滤波控制系数a就成为了信号噪声水平的函数,即有自适应能力。再结合自回归算法,就可有效地滤出噪声,提高信噪比。 同时利用分形结构的物体具有自相似性和空间填充2个特点,设计的分形侦察天线可实现天线宽频(或多频)化和小型化的目的,在机载和舰载侦察设备中将有广泛的用途。分形信号的分层结构、空间的间隙性和时间的间歇性可为复杂多变战场电磁环境的建模和仿真提供重要的理论和技术基础,同时还会增加模拟的逼真度,细化仿真的颗粒度和增强动态演化推演效果,可检验侦察系统在真实环境中的适应性。 分形信号具有自相似和无标度等特性,因此,下面从信号和接收的角度探索基于分形理论的非线性对抗技术研究。 通信对抗研究认为,干扰信号与通信信号的频谱一致、波形相似对信号干扰噪声的影响最大。对于确定性分形信号一般通过迭代函数产生,因此可利用侦测到的信号作为源函数,信号在传输过程中,具有一定的相关量,含有许多不变参数,即存在仿射冗余度,经过适当变换(变形、旋转、平移),再进行迭代,得到的分形干扰信号一方面与通信信号具有较多的相似度,另一方面又具有自相似的特性,从而可有效地污染通信信号。对于随机分形信号,可通过迭代程序加入随机条件产生,因此利用非线性中的微扰论和相变理论使分形信号诱发通信信号产生随机振荡,从平稳信号变为非平稳信号,使得接收系统无法有效接收通信信号,达到干扰的目的。 在目前的通信对抗中,主要对接收系统进行有效干扰和攻击,利用分形的瞬态特性和自相关等非线性效应,从时、频、空维等多角度,增加干扰信号抗接收处理算法的免疫能力,使接收机处于非正常工作状态,造成接收机不能有效地解调信号,恢复所需信息。 目前,对于大多数噪声信号处理,功率谱分析方法是噪声研究中最常用的,也是经典的分析方法,其频率指数γ已成为表征噪声特性的重要表征参量。通过研究发现,基于傅里叶变换的功率谱密度只是信号的全局性描述,是一种不完备描述,不能有效消除信号的局部奇异性和不规则程度。而分形具有处处不可导的特性,因此很难通过一般信号处理算子消除。因此,利用分形信号可以使功率谱分析失效。下面以典型随机分形信号——分数布朗信号的频、时特性为例来分析对处理算法的影响。 分数布朗信号SBJam(t)是零均值非平稳高斯信号,且具有以下形式的相关函数: E[SBJam(t)SBJam(s)]= (5) 式中:σBJam2为均方值;自相似参数H满足:0 在频域,作为非平稳过程,分数布朗信号不遵循一般意义的功率谱形式,其功率谱为: (6) 式中:γ=2H+1。 此外,从时域来分析,分数布朗运动具有自相似性,这表现在对任意α>0,有: (7) 从上式可见,分数布朗信号是时间(或空间)长程相关、功率谱满足指数规律、增量服从正态分布的非平稳随机信号,常规基于信号的不相关性的信号处理算法(如自回归华东平均(ARMA)法、谱估计和长时间积累方法等)就不能有效剔除分数布朗信号,因而分数布朗信号可有效污染通信信号,达到非线性干扰的目的。 另外分形信号是一种非平稳信号,具有瞬态效应。瞬态效应是指信号瞬态变化剧烈,可造成前端部分电子器件进入非线性区,或者直接达到饱和状态,从而达到致使前端信道进入无序状态,影响其正常接收。 通过对分形理论在通信对抗的应用初探,开启了一扇非线性侦察和对抗的大门,为通信对抗注入了新鲜理论,可能为通信对抗跨越式发展开辟一条希望之道。 [1] 栗苹,赵国庆,杨小牛.信息对抗技术[M].北京:清华大学出版社,2008. [2] 阚德鹏,贾翠霞.复杂战场电磁环境模拟技术研究[J].中国电子科学研究院学报,2009,6(4): 598-599. [3] 陈鲲,陈云秋,陈世友.海杂波建模与仿真[J].舰船电子工程,2009,176(2): 95-97. [4] 赵健,雷蕾,蒲小勤.分形理论及其在信号处理中的应用[M].北京:清华大学出版社,2008. [5] 吕铁军,郭双冰,肖先赐.基于复杂度特征的调制信号识别[J].通信学报,2002,23(1):111-115. [6] 布和额尔敦,韩峰.基于分形维数的自适应信号滤波方法[J].地球物理学进展,2008,23(2),627-630. [7] 胡刚,朱世华,谢波.CDMA2000中基于分形滤波的信道估计方法[J].电子学报,2004,32(2):1-4. Research into The Communication Countermeasure Technology Based on Fractal Theory PENG Xiao-ming1,YOU Jing-yun1,2 (1.No.36 Research Institute of CETC,Jiaxing 314033,China;2.Science and Technology on Communication Information Security Control Laboratory,Jiaxing 314033,China) Based on fractal theory and fractal characteristics,this paper researches into the application of fractal theory to communication reconnaissance from two aspects of burst signal detection and fractal filtering,aiming at the transmitting and receiving characteristics of communication signals,proposes fractal signal jamming technology by using self-similarity properties of fractal,and analyzes the feasibility from respects such as time domain,frequency domain and transient state,etc.,which opens a new door for the communication countermeasure. fractal;communication countermeasure;signal detection 2016-10-11 TN975 A CN32-1413(2017)02-0035-04 10.16426/j.cnki.jcdzdk.2017.02.0092 基于分形理论的侦察技术
3 基于分形理论的对抗技术
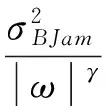
4 结束语
