国际原油价格拐点分析及统计推断

柴 建，卢全莹，周友洪，邢丽敏，汪寿阳

(1. 西安电子科技大学经济与管理学院，陕西 西安 710126；2. 中国科学院大学经济与管理学院，北京 100190；3. 陕西师范大学国际商学院，陕西 西安 710062；4. 湖南大学工商管理学院，湖南 长沙 410082)



国际原油价格拐点分析及统计推断

柴 建1，卢全莹2，周友洪3，邢丽敏4，汪寿阳2

(1. 西安电子科技大学经济与管理学院，陕西 西安 710126；2. 中国科学院大学经济与管理学院，北京 100190；3. 陕西师范大学国际商学院，陕西 西安 710062；4. 湖南大学工商管理学院，湖南 长沙 410082)

原油具有战略和金融双重属性。原油价格波动分析一直是全球的研究热点，特别是油价大幅波动的拐点对能源金融行业的相关人员至关重要。基于此，本文对国际原油价格拐点分析及统计推断进行了探索性研究，以原油月度价格作为研究对象，集成构建PPM-KM国际原油价格拐点分析模型以适应国际原油价格拐点后验概率的测算、聚类及识别。首先，基于PPM模型测算出国际原油价格序列突变的后验概率，并结合K-Means聚类方法给出原油价格突变后验概率识别阈值，对原油价格的历史突变进行识别和分析。其次，以比较符合描述突变规律的泊松分布，对数-正态分布，幂律分布三种分布，构建国际原油价格拐点统计推断模型，对原油月度价格的突变规律进行概率模拟并比较分析。结果表明，1986年-2015年期间共发生37次显著的油价突变。在不同的时点，市场供需结构的失衡、突发地缘政治事件、美元指数、全球经济发展情况分别成为油价突变的主因。通过对油价突变点时间间隔的分布拟合，本文初步认为国际原油月度价格拐点的时间间隔服从幂律分布的假设是合理的。

原油价格；拐点；PPM；K-Means聚类；幂律分布

1 引言

随着原油期货市场、原油场外衍生品市场的迅猛发展，原油经济日趋金融化。油价对各种事件的反应越来越灵敏，突变频发，对经济稳定发展产生了巨大的冲击。2014年6月以来，国际原油价格“跌跌不休”，呈波浪震荡。全球原油供应过剩，OPEC组织坚持不减产成为油价下跌的主要原因。原油价格的持续大幅下跌对全球经济都产生了较大影响。一方面，原油下跌对沙特、俄罗斯等出口国的经济发展带来沉重打击，特别是俄罗斯在卢布下滑和油价下跌的双重作用下，经济发展严重受阻。另一方面，原油下跌却为中国这样的原油进口国家的能源价格改革及能源基础设施建设提供机遇。原油价格的大幅下跌，大大降低了成本因素对中国能源领域改革的制约。同时，为中国扩大石油战略储备，加快能源基础设施建设提供了条件。其次，原油价格下跌为投资人带来了较大利润空间。投资者把握油价下跌趋势，看空持有，将会带来不菲的收益。可见，分析国际原油价格走势，识别原油价格的趋势变点将有利于国家和企业以及投资者把握市场走势，规避投资风险，进行正确的投资决策。在原油价格趋势分析中，价格拐点的识别和分析变得十分重要，是具有重要理论及现实意义的科学问题。

由于油价波动问题是对原油市场进行风险分析的基础，近几十年来油价波动方面的研究成果颇丰，并且油价波动问题越来越成为各国政府和原油产业界倍加关注的重点。国内外已有大量文献对原油价格波动的机理、风险特征及油价波动的宏观经济影响等问题进行了广泛的研究。主要分为两种类型，一种是单纯利用油价数据基于计量经济技术来分析油价的波动性[1-4]。其次，从经济学理论出发对油价的波动性进行定性分析，也是认识原油价格波动本质特征的另一种重要方法[5-10]。

虽然在油价变动趋势预测及其影响效应分析方面已存在大量的研究成果，但油价的突变识别与分析、油价系统均衡结构变化方面的研究却很少。张殉等[11]基于结构性断点检验和常收益事件分析模型，分析了伊朗革命、海湾战争和伊拉克战争三次重大突发事件对原油价格的影响。Chai Jian等[12]建立了油价系统的BVAR—TVP模型来考察油价核心影响因素对油价的影响时滞及影响力的动态变化。结果表明，美元指数始终是油价波动的重要因素且控制力逐渐加大，中国石油净进口对油价的影响自2006年开始才显著出现。其实，变点问题自上世纪70年代被Canova提出以来一直是一个热门课题[13]。近几十年，关于变点问题的研究无论在理论还是在应用方面皆有了快速的发展，识别和处理变点问题的方法包括Choy检验、Bayes方法、极大似然比方法、Schwarz信息准则法、PPM (Product Partition Model)等，在特定的假设条件下，这些方法均能有效地判断及识别出均值变点、概率变点及模型变点[14-19]。但其应用在原油价格分析方面的研究还很少，柴建等[20]利用PPM模型对国际历史油价及相关影响变量的突变进行识别和分析。

综上，近些年国内外学者对原油市场价格波动进行了各方面的研究，为国际原油市场建立有效的价格形成机制、风险管理以及能源政策的制定提供了大量的资料。但是就目前的研究文献来看，对于油价波动状态变动的识别及在不同状态下油价波动对经济影响的对比分析却很少，特别是对油价拐点的分析及预测文章更是寥寥无几。同时，因为商品价格的突变应该与数学、物理学、化学、生物学、工程技术等学科中的突变有着不同的定义。所以，截止目前为止，对于原油价格的突变并没有一个确切的定义。柴建等[20]基于PPM思想构建了国际原油季度价格的突变识别和分析模型，但是在模型构建过程中对于价格容忍阈值的选择还存在改进空间。其次，在模拟事件发生的概率分布模型构建中，无论是研究系统动力学还是预测模型，学者们常常把人类行为简化为可以使用泊松过程描述的稳态随机过程。大部分学者也一直假设油价的拐点时刻点服从泊松分布[21]。但是，随着科技的不断发展，大量的数据可以获得以便进行统计和分析。2006年nature上发表了一篇开创性的文章，清晰揭示了人类行为活动对泊松分布的偏离[22]。科学家进一步研究了与人类活动相关的城市人口分布，互联网信息，市场交易，金融，通信，自然灾害等一系列问题，发现人类的很多活动并不是简单的泊松分布，而是具有厚尾特征的幂律分布。幂律分布允许短时间内事情频繁发生，接着很长的一段时间里沉寂下来。相邻两个事件的时间间隔分布存在满足反比幂函数的厚尾特性[23]。特别是，大量研究证明国际原油价格的走势和股票交易市场存在很大的相关性[24-25]。同时，也有研究表明股票交易时间间隔分布特征服从幂律分布[26-27]。因此，本文猜想国际原油价格拐点的时间间隔是否也服从幂律分布？

本文以国际原油月度价格作为研究对象，通过对PPM模型进行扩展，集成构建PPM-KM国际原油价格拐点分析模型以适应国际原油价格拐点后验概率的测算、聚类及识别。首先，基于PPM模型测算出国际原油价格序列突变的后验概率，并结合K-Means聚类方法给出原油价格突变后验概率识别阈值，对原油价格的历史突变进行识别和分析。其次，以比较符合描述突变规律的泊松分布，对数-正态分布，幂律分布三种分布，构建原油价格拐点统计推断模型，对原油月度价格的突变规律进行概率模拟并比较分析。

2 模型构建

商品价格的突变应该与数学、物理学、化学、生物学、工程技术等学科中的突变有着不同的定义。有了定义就有了对商品价格突变进行识别和分析的标准，这样的分析才更加具有科学性。遗憾的是，这样的定义(标准)在前人有关价格突变的研究中并未出现。因此，本文通过对柴建等[20]引入的PPM(Product Partition Model)原油价格突变识别模型进行扩展，结合K-Means聚类方法，集成构建PPM-KM模型对原油价格的历史突变点进行识别和解析，并引入幂律分布，泊松分布，对数-正态分布对价格的突变规律进行模拟和比较分析。

2.1 PPM模型

由于篇幅原因，PPM模型的具体算法和技术见Loschi等[28-29]及柴建等[20]。油价突变概率的不同对应着相应油价突变发生时间前后的油价绝对差不同，企业或政府对此绝对差的容忍度将有个界限，将这一界限所对应的油价突变概率大小作为油价突变概率的容忍阀值大小。由于不同政策环境、不同经济环境下不同政府、不同企业对油价突变大小的容忍度均不会相同，所以基本的PPM模型的容忍阀值一般都是主观假定。但为了进一步提高容忍阀值确定的客观性，本文对PPM模型进行扩展，结合K-Mean聚类方法，集成构建了PPM-KM整合模型。

2.2 拐点时间间隔的分布选择

原油作为一种特殊的商品，其拐点的出现一般都伴随着突发事件的发生，这些突发事件改变了人们的预期进而影响到需求，反映到原油价格上便是拐点的出现。由于拐点出现的时间间隔服从什么分布并没有得到完全准确的证明，所以本文通过分析历史原油价格的突变点规律，引入三种可能的分布(指数分布、幂律分布、对数-正态分布)，分别对原油价格拐点进行分析和推断。

2.2.1 指数分布

根据突发事件的发生特点，每一个突发事件基本相互独立；而且下一次突发事件的到达时完全不确定的，与时间长短无关；同时在很短的时间内很难出现多次突发事件，即使有多于一个的突发事件，起关键作用的还是其中一个；有很多学者对突发事件的这种特点进行了研究，得到其发生的时刻点很符合泊松分布的结论(泊松时间流特性：1、平稳性(到达概率与时间段无关)，2、稀有性(短时间内最多出现1次)，3、无后效性(不重叠时间段互相独立)，4、微分性)。而泊松分布和指数分布具有紧密的关系，如果一个事件的发生时刻服从泊松分布，则其相邻两时刻的时间间隔服从指数分布。

假定油价拐点间的时间间隔服从参数为λ的指数分布，分布密度函数为：

f(x|λ)=λe-λx

(1)

累积分布函数为：

F(x|λ)=1-e-λx

(2)

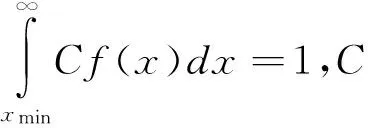
f(x)=e-λx

(3)

泊松过程作为经典的刻画人类活动模式的手段，经常被不加仔细评估地应用于实际问题中[30]。最近几年，越来越多的数据显示泊松分布不能完全解释由人类行为驱使的复杂活动。泊松过程产生的事件时间间隔大体上是均匀的，而当间隔时间分布具有明显偏离指数分布的胖尾特征时，幂律分布函数可以更好的拟合。原油价格拐点的时间间隔是否也服从幂律分布过程？在2.2.2中我们假定油价拐点的时间间隔服从幂律分布，试图与泊松分布过程和对数正态分布进行比较分析。实际中很少有所有的观察值都服从幂律分布，更多的时候我们说数据服从幂律分布是指大于最小值的那些值服从幂律分布。也就是说，我们是指分布的尾部服从幂律分布。

2.2.2 幂律分布

对幂律分布的长尾思想做出重要贡献的是哈佛大学的语言专家Zipf和意大利的经济学Pareto。Zipf在1932年研究英文单词出现的频率时候，发现如果把单词出现的频率按由大到小的顺序排列，则每个单词出现的频率与它的名次的常数次幂存在简单的反比关系：P(x)=x-α，这种分布就称为Zipf定律。分形几何学创始人Mandelbrot[31]对Zipf定律进一步修订，使它更符合实际情况。意大利经济学家Pareto对个人收入的统计分布进行了研究，研究表明少数人的收入要远多于大多数人的收入，提出了著名的80/20法则。个人收入X不小于某个特定值α的概率与T的常数次幂存在反比关系：P[X≥x]～x-α，称为Pareto定律[32]。Zipf定律和Pareto定律的结合称为幂律分布。1999年关于人类行为空间标度率的两篇震惊世界的文章分别发表在Science和Nature上[33-34]，受这两篇文章的影响，大量关于人类行为动力学幂律分布的研究涌现。

幂律分布的一般形式为：

p(x)～x-α

(4)

其中，α为标度参数，一般地，2<α<3(α的取值也能不在这个区间，允许存在偶然情况)，称X服从幂律分布。

幂律分布一般分为两大类：连续型和离散型。对于连续型幂律分布，概率密度函数形式如下：

p(x)dx=Pr(x≤X≤x+dx)=Cx-αdx

(5)

(6)

其累积分布函数为：

(7)

离散型幂律分布的概率密度函数为：

p(x)=Pr(X=x)=Cx-α

(8)

离散型幂律分布概率密度函数可以写为：

(9)

(10)

其中，xmin是X的最小值，α是唯一的分布参数。

参数估计

Kolmogorov-Smirnov(KS)是用于估计数据真实分布与理论分布的拟合程度的统计方法，此方法是一种有效的非参数检验方法，可定量计算非正态分布数据的两种分布之间的最大距离D：

(11)

连续型数据根据极大似然法，公式(6)可写为：

(12)

据根据极大似然法对(12)取对数得到：

(13)

离散型数据根据极大似然法对(10)取对数得到：

(14)

不是所有的数据都服从幂律分布，所以在假设数据服从幂律分布之前要进行最优拟合检验。假定油价拐点间的时间间隔服从分布参数为α的连续型幂律分布，利用公式分别计算出xmin和α的估计结果。在拟合优度检验时候，用自助法分别计算KS统计抽样结果Ds，统计Ds大于D的比例，记为P。如果P值大于0.1时，说明数据是服从幂律分布函数的；反之，则不符合幂律分布。

在对幂律分布进行检验的时候我们需要注意的一个问题是，P值很大并不能代表幂律分布是一个正确的分布。原因有两个。首先，有可能其他类型的分布也能够很好的拟合数据，甚至比幂律分布更好。其次，当我们的观察数据量n相对较少时(n≤100)，可能导致的结果是虽然P值很大但对所研究的数据而言，幂律分布可能是一个错误的模型。这并不能说是幂律分布的一个缺陷，而是提醒我们如果数据量很少时会很难排除服从幂律分布的可能性，我们应该谨慎的处理。因此，为了进一步证明幂律分布的合理性，本文又引入了另一个具有厚尾特征的分布——对数正态分布，比较三种分布模型的拟合优劣情况，并进行相应的拟合优度检验[35]。

2.2.3 对数—正态分布

假定油价拐点间的时间间隔服从参数为μ和σ的对数正态分布，概率密度函数为：

(16)

累积分布函数为：

(17)

其中，x>0，μ是位置参数，σ>0为尺度参数，erf表示误差函数。

(18)

3 实证分析

3.1 确定突变点

将国际原油价格月度数据(1986年1月—2015年12月(数据来源：EIA))代入模型，利用R软件bcp程序包，计算得出油价的后验均值及突变点后验概率，具体结果见表1。为了进一步提高容忍阀值确定的客观性，本文通过对PPM进行扩展，利用K-Means聚类方法对容忍阀值进行分析，将所有突变点的后验概率进行聚类，计算得到油价突变概率的容忍阀值为0.394。由图1和表1可见，聚类后突变点一共为37个，分别为1990年7月，1990年12月，1997年12月，2001年9月，2004年7月，2005年2月，2005年5月，2005年6月，2006年3月，2006年8月，2007年6月，2007年8月，2007年9月，2007年10月，2008年2月，2008年4月，2008年7月，2008年8月，2008年9月，2008年10月，2008年11月，2009年2月，2009年4月，2009年5月，2009年9月，2010年9月，2010年10月，2011年2月，2011年7月，2011年10月，2012年4月，2012年5月，2013年6月，2013年9月，2014年9月，2014年11月，2015年7月。

图1 原油月度价格及其后验均值、突变点识别及发生概率PPM计算结果

时间点时间间隔原油价格突变概率后验均值Jul-19900.91819.35Dec-199050.64829.8Dec-1997840.44418.97Sep-2001450.70227.1Jul-2004340.78639.18Feb-200570.43848.45May-200530.42651.5Jun-200510.39456.42Mar-200690.9662.3Aug-200650.82271.45Jun-2007100.61466.08Aug-200720.43873.77Sep-200710.54278.53Oct-200710.51887.12Feb-200840.9992.99Apr-200820.988109.18Jul-200830.992131.08Aug-200810.48113.41Sep-200811107.31时间点时间间隔原油价格突变概率后验均值Oct-200810.99876.55Nov-200810.98457.13Feb-200930.56842.02Apr-200920.7647.91May-200910.561.11Sep-200940.88468.36Sep-2010120.43677.33Oct-201010.47881.3Feb-20114187.47Jul-201150.98499.1Oct-201130.99886.05Apr-201260.614101.17May-201210.42694.51Jun-2013130.84894.04Sep-201330.53104.08Sep-2014120.85696.3Nov-201420.99879.28Jul-201580.86253.12

表2 原油价格突变点所对应的历史突发事件

为了进一步解释和分析PPM-KM整合模型挑选出的突变点，我们试图找出所有突变点所对应的历史突发事件，如表2所示。

3.2 拟合分布

本文利用R软件包poweRlaw进行拟合，可以计算得到指数分布的参数估计值为xmin=1,λ=0.12784,D=0.2221695；对数—正态分布的参数估计值为xmin=1,μ=0.86352,σ=1.48895,D=0.05913；在拟合幂律分布时，首先利用自助法抽样10000次，计算得到幂律分布假设检验的p值为0.8487，表明接收原假设，原油价格拐点的时间间隔数据服从幂律分布。同时计算得到参数的估计值xmin=3,α=1.9346,D=0.07272774。

由表3可以看出，通过LR的符号可以做出判断，指数分布被剔除，对数-正态分布没有被剔除。但对数似然比的显著性检验P值分别为0.22，0.96，都大于0.1，表明两个替代分布的LR都不是十分显著，LR的符号可能是不稳定的，我们不能十分肯定的说幂律分布比替代分布好或者不好。图2，显示了幂律分布、对数-正态分布和指数分布三种分布的拟合效果。随着时间间隔增大，仍有拐点出现的可能，指松分布不能很好地拟合数据的尾部，而幂律分布可以较好的拟合。原油价格拐点的时间间隔的概率统计分布在远离平均值处仍有较高的发生概率，可能是一种厚尾分布，在许多情况下是幂律分布。目前常用的一些统计函数如指数分布、对数-正态分布等不能有效地拟合出拐点时间间隔分布的尾部，往往不能有效的预测拐点出现的概率。直观地看，实际累积概率分布在一定区间内呈线性，具备了幂律分布的必要条件。所以，本文得出如下结论：国际原油月度价格拐点的时间间隔服从幂律分布的假设是合理的。但由于数据量较少，不能排除存在替代分布的可能性。

4 结语

本文引入PPM 模型对国际原油月度价格的突变进行识别和分析，并通过对PPM模型扩展，利用KM聚类方法对商品价格变动容忍阈值进行聚类和识别，集成构建了PPM-KM整合模型。结果表明，1986年-2015年共发生37次显著的油价突变。在不同的时间点，市场供需结构的失衡，突发的地缘政治事件，美元指数，全球经济的发展情况都分别是油价突变的主因。同时，考虑到油价的非线性和内部变化的高度复杂性，是在此基础上的人类心理和资金的一种博弈行为，使得国际原油价格拐点的时间间隔的概率分布表现出幂律分布特征，本文将幂律分布引入原油价格拐点分析中。通过与泊松分布，对数-正态分布比较分析，初步认为国际原油月度价格拐点的时间间隔服从幂律分布。如果将Poisson过程作为描述原油价格的跳跃过程，实际上隐含着默认在任何一个时刻原油价格发生跳跃的概率都是相同的，显然这与实际情况并不相符。而本文引入的幂律分布则可以模拟得到原油价格在较长时间不发生跳跃过程的情形，也可以得到跳跃过程在短时间内密集发生的状况，这更加符合现实情况。幂律分布的引入使得原油价格在任何一个时点发生跳跃的概率并不相同，而这种不相同的概率赋予是依赖于当时市场所处的状态。这表明市场存在一定的记忆性，即今天市场的现状并非凭空而来，而是基于其历史的市场，这与现实世界的情形更为贴切。幂律分布过程获得的原油价格某一时间拐点发生的概率可以成为实际原油市场分析的新指标，而且该指标来源于市场本身，获取和应用起来简便易行。从实证分析角度来说，原油价格波动服从泊松分布显得对极端事件无可奈何，因而需要引入一种厚尾分布进行修正，而幂律分布则可以较好地解决这个问题。虽然由于突变点数据有限，该幂律分布模型仍需更多详实的数据进一步实证或修正，但该概率分布模型提供了国际原油价格拐点时间间隔分析的新视角。

表3 三种分布比较的检验结果

注：LR为对数似然比，LR为正表示幂律分布比替代分布好；moderate表明幂律分布很好拟合了实际数据，但是也有其他可替代的分布。

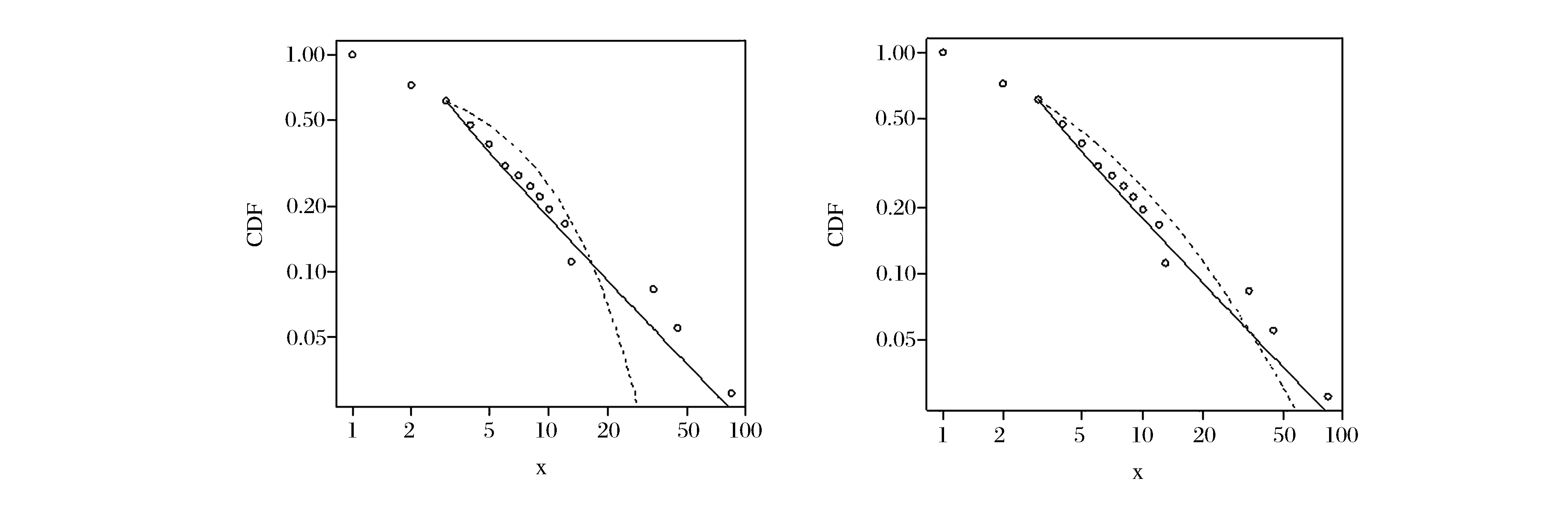
图2 左幂律分布(实线)和指数分布(虚线)，右幂律分布(实线)和对数-正态分布(虚线)尾部CDF拟合图(双对数坐标下)

[1] Hou Aijun , Suardi S. A nonparametric GARCH model of crude oil price return volatility[J]. Energy Economics, 2012, 34(2):618-626.

[2] Mohammadi H, Su Lixian. International evidence on crude oil price dynamics: Applications of ARIMA-GARCH models[J]. Energy Economics, 2010, 32(5):1001-1008.

[3] 柴建,郭菊娥,龚利,等. 基于Bayesian-SV-SGT模型的原油价格‘Value at Rsik’估计[J]. 系统工程理论与实践. 2011, 31(1):8-17.

[4] Askari H, Krichene N.Oil price dynamics (2002-2006)[J]. Energy Economics, 2008, 30(5):2134-2153.

[5] Kilian L. Not all oil price shocks are alike: Disentangling demand and supply shocks in the crude oil market[J]. American Economics Review, 2009, 99(3): 1053-1069.

[6] Salisu A A, Fasanya I O. Modelling oil price volatility with structural breaks[J]. Energy Policy, 2013, 52:554-562.

[7] Ji Qiang, Fan Ying. How does oil price volatility affect non-energy commodity markets? [J]. Applied Energy, 2012, 89(1):273-280.

[8] 吴刚,魏一鸣.突发事件情景下的中国战略石油储备应对策略研究[J].中国管理科学,2011, 19(2):140-146.

[9] 吴振信,薛冰,王书平. 基于VAR模型的油价波动对我国经济影响分析[J].中国管理科学,2011,19(1):21-28.

[10] 王书平,吴振信.布伦特原油价格季节性波动分析[J].中国管理科学, 2008,16(1):48-52.

[11] 张殉,余乐安,黎建强,等.重大突发事件对原油价格的影响[J].系统工程理论与实践,2009, 29(3):10-15.

[12] Chai Jian, Guo J E, Meng Lei, et al. Exploring the core factors and its dynamic effects on oil price: An application on path analysis and BVAR-TVP model[J]. Energy Policy, 2011, 39(12):8022-8036.

[13] Canova F.Detrending and turning points[J]. European Economic Review, 1994, 38(3-4): 614-623.

[14] Choy J H C, Broemeling L D. Some Bayesian inferences for a changing linear model[J]. Technimetrics, 1980, 22(1):71-78.

[15] Dey D K, Ghosh S K, Chang Hong.Measuring the effect of observations using the posterior and the intrinsic bayes factors with vague prior information[J]. Sankhy:The Indian Journal of Statistics,1997,59(3):376-391.

[16] Inclan C. Detection of multiple changes of variance using posterior odds[J]. Journal of Business and Economic Statistics, 1993, 11(3):289-300.

[17] Inclan C, Tiao G C. Use of cumulative sums of squares for retrospective detection of changes of variance[J]. Journal of the American Statistical Association, 1994, 89(427): 913-923.

[18] Ferreira P E. A Bayes analysis of a switching regression model: Known number of regimes[J]. Journal of the American Statistical Association, 1975, 70(350):370-374.

[19] Hamilton J D. A new approach to the economic analysis of nonstationary time series and the business cycle[J]. Econometrica, 1989, 57(2):357-384.

[20] 柴建,朱青,张钟毓,等.国际油价识别及分析[J].中国人口资源与环境, 2014, 24(1):109-117.

[21] D’Agostino R B, Stephens M A.Goodness-of-fit techniques[M]. New York: Marcel Dekker, 1986.

[22] Barabási A L. The origin of bursts and heavy tails in human dynamics[J]. Nature, 2005, 435(7039):207-211.

[23] Vázquez A, Oliveira J G, Dezsö Z, et al. Modeling bursts and heavy tails in human dynamics[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2006, 73(3):80-98.

[24] Cunado J, Gracia F P D. Oil price shocks and stock market returns: Evidence for some European countries[J]. Energy Economics, 2014, 42(1):365-377.

[25] Kilian L, Park C. The impact of oil price shocks on the U.S. stock market[J]. International Economic Review, 2009, 50(4): 1267-1287.

[26] Xavier G, Parameswaran G, Vasiliki P, et al. A theory of power-law distributions in financial market fluctuations[J]. Nature, 2003, 423(6937):267-270.

[27] Zhou Weixing. Universal price impact functions of individual trades in an order-driven market[J]. Quantitative Finance, 2007, 12(8):1253-1263.

[28] Loschi R H, Cruz F R B.An analysis of the influence of some prior specifications in the identification of change points via product partition model[J]. Computational Statistics & Data Analysis, 2002, 39 (4):477-501.

[29] Loschi R H, Cruz F R B, Iglesias P L, et al. A Gibbs sampling scheme to the product partition model: An application to change point problems[J]. Computers & Operations Research, 2003, 30 (3):463-482.

[30] 周涛,韩筱璞,闫小勇,等.人类行为时空特性的统计力学[J].电子科技大学学报,2013, 42(4):481:540.

[31] Adamic LA.Zipf,power-laws,and Pareto-AranRingtutorial[R/OL].http://www.hpl.hp.com/research/idl/papers/ranking/ranking, 2000.

[32] 张济中.分形[M].北京:清华大学出版社,1997,348.

[33] Albert R, Jeong H, Barabási A L. Internet: Dianmeter of the worldwide web[J]. Nature, 1999, 401(6749): 130-131.

[34] Barabási A L, Albert R.Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512.

[35] Clauset A, Shalizi C R. Newman M E J. Power-law distributions in empirical data[J]. Annals of Applied Statistics, 2009, 51(4): 661-703.

[36] Vuong Q H. Likelihood ratio tests for model selection and non-nested hypotheses[J]. Econometrica, 1989, 57(2):307-333.

Analysis and Statistical Inference of Crude Oil Price Change Points

CHAI Jian1，LU Quan-ying2，ZHOU You-hong3，XING Li-min4,WANG Shou-yang2

(1.School of Economics and Management, Xidian University, Xi’an 710126, China;2.School of Economics and Management, University of Chinese Academy of Sciences, Beijing 100190，China;3.International Business School，Shanxi Normal University, Xi’an 710062, China; 4.Business School,Hunan University,Changsha 410082,China)

The crude oil is of dual attributes, strategic and financial. Oil price fluctuations attract attention around the world, especially the oil price fluctuation change point is considered more important for energy finance industry. Based on this idea, an exploratory research direction is introduced in this paper. Monthly international crude oil prices were taken as the study objective and the PPM-KM integration model was established by extending product partition model (PPM) to adapt to measure, cluster, and identify the posterior probability of change points of international crude oil price. First, this paper measured the mutations posteriori probability of the oil price based on the PPM model in order to distinguish and analyze the mutations of the oil price, and gave the result of the tolerance threshold and mutations of commodity price combined with K-Means clustering method. Second, the Poisson distribution, power-law distribution, and logarithmic-normal distribution were used to build statistical inference model to the catastrophes description, and then corresponding probability distribution functions for simulation and analyses of the monthly crude oil price change point trends were constructed. The results showed that there were 37 significant breaking points in the period of 1986 to 2015. At different time points, the imbalanced structure of market supply and demand, unexpected events, the dollar index, the global geopolitical economic development situation the main oil mutations as the main cause of crude oil price fluctuation respectively. By fitting the distribution of the time interval of change points, this paper preliminary think the time interval of monthly international crude oil price change points obeys power-law distribution assumption is reasonable.

crude oil price; change point; PPM; K-Means; power-law distribution; Poisson distribution; logarithmic-normal distribution

1003-207(2017)05-0033-09

10.16381/j.cnki.issn1003-207x.2017.05.005

2016-03-23；

2016-07-31

国家自然科学基金面上项目(71473155)；陕西师范大学中央高校特别资助项目(14SZTZ03)；陕西省青年科技新星计划项目(2016KJXX-14)；西安电子科技大学2016年度基本科研业务费自由控索类项目(JB160603)

卢全莹(1991-)，女(汉族)，天津武清人，中国科学院大学经济与管理学院，博士生，研究方向：能源金融、能源经济、宏观经济分析与建模、预测，E-mail:luquanying0705@163.com.

F062.1; F831.5

A