刚体极限平衡法与有限元法在重力坝岸坡坝段抗滑稳定计算中的对比分析
2017-05-30容晓
容晓

【摘 要】重力坝是由混凝土或浆砌石修筑的大体积挡水建筑物,其在水压力及其他荷载作用下,主要依靠坝体自重产生的抗滑力来满足稳定要求。抗滑稳定计算是重力坝设计中最重要的一项内容,而岸坡坝段的抗滑稳定计算由于受三向荷载的作用,其计算比河床坝段更为复杂。以西部某水利工程为例,分别利用刚体极限平衡法和有限元法计算重力坝岸坡坝段沿坝基面的抗滑稳定,并对这2种方法的计算结果进行对比分析,为工程决策提供依据。
【关键词】刚体极限平衡法;有限元法;重力坝;岸坡坝段;抗滑稳定分析
【中图分类号】TV642.3 【文献标识码】A 【文章编号】1674-0688(2017)05-0125-04
0 引言
抗滑稳定是否满足要求直接关系到大坝的安全,是重力坝设计中最重要的一项内容。岸坡坝段由于受到上游水压力和重力作用,有向下游及河床滑动的趋势,其抗滑稳定性往往较河床坝段更为不利。现行规范中分析抗滑稳定的基本方法为刚体极限平衡法[1],该法考虑了坝体混凝土与基岩间的摩擦力和凝聚力,物理概念明确,拥有长期的工程实践经验,不足之处是对于像折面阶梯状建基面的重力坝岸坡坝段这类不便于简化成平面问题的三维空间结构,其计算过程相对复杂。而有限元法是把求解区域划分成许多小的在节点处互相连接的单元,然后在单元的节点上施加荷载、约束,进而进行求解。弹性理论有限元法在力学模型上是近似的,在数学解法上是严格的,它是一种综合能力很强的计算方法[2]。该方法在计算三维空间结构时有一定的优势,是对刚体极限平衡法的补充和完善。笔者分别采用上述2种方法对西部某水利工程重力坝的岸坡坝段进行沿坝基面的抗滑稳定计算,并对这2种方法的计算结果进行对比分析。
1 工程概况
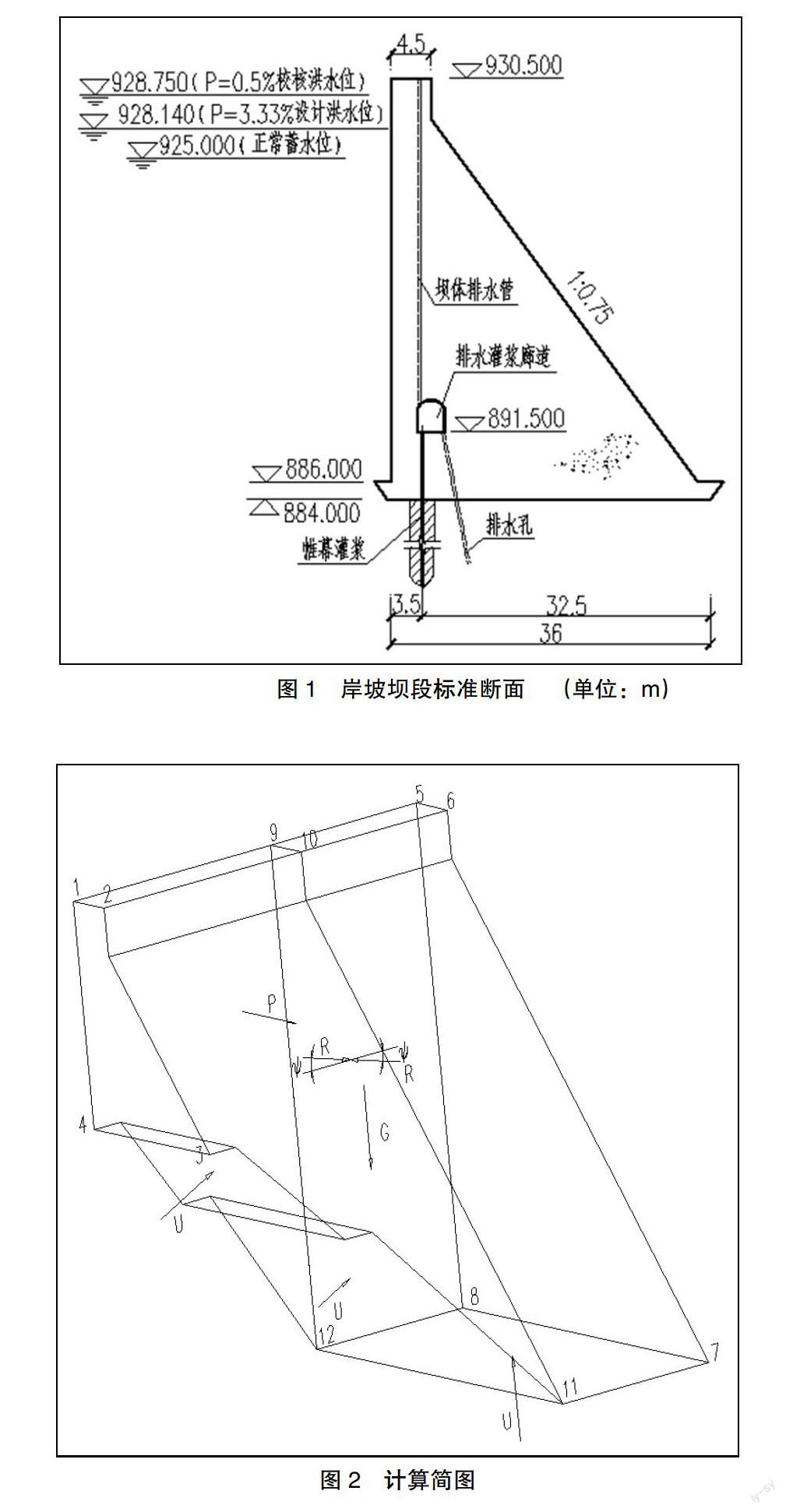
西部某水利工程是一座以村镇供水、灌溉为主的综合利用水库,主要由挡水坝、消力池、放水设施、人饮供水管道等组成。总库容为140.1万m3,为小(1)型水库,Ⅳ等工程,挡水坝等主要建筑物按4级建筑物设计。水库正常蓄水位为925 m,设计洪水位为928.14 m(P=3.33%),校核洪水位928.75 m(P=0.5%)。坝顶高程为930.5 m,最大坝高46.5 m,坝长157 m,坝顶宽4.5 m。上游坝坡896 m高程以上铅直,896 m高程以下为1∶0.2;下游坝坡926 m高程以上铅直,926 m高程以下为1∶0.75。基础排水灌浆廊道设于坝内上游侧,城门洞形,断面尺寸为3 m×3.5 m(宽×高),廊道上游距离坝轴线3 m。坝基基础处理采用固结灌浆和帷幕灌浆,为有效地降低大坝基底扬压力,在基础排水灌浆廊道布置一排排水孔。岸坡坝段标准断面如图1所示。
河谷两岸属中低山地貌,河谷呈“V”字形,两岸地形基本对称。坝址区分布的岩性较为简单,为三叠系中统百逢组第二段泥质粉砂岩夹砂岩,岩体为强~弱风化。岩体的透水性随着深度的增加而减弱,其中强风化岩体多属中等透水性,局部属弱透水性;弱风化岩体多属弱透水性,局部属中等透水性;微风化岩体基本属弱透水性。坝基岩层倾向下游偏右岸,倾角一般为60°~65°;坝区节理发育主要有四组,裂面均粗糙、稍起伏,微张~闭合狀,延伸长度一般为1~3 m。随着埋深变化,节理裂隙宽度由上至下从张开逐步变化为闭合,上部裂隙面铁锰质渲染强烈,强风化带多夹泥。节理相互间贯通性较差、延伸较短,不会与层面形成较大的楔体,不会对坝基的抗滑稳定产生较大影响;坝基无对抗滑稳定不利的结构面组合,坝基不存在缓倾角结构面控制的坝基抗滑稳定问题。
2 计算方法
为对比分析计算结果,分别采用刚体极限平衡法和有限元法对重力坝岸坡坝段的控制工况(即设计洪水工况)进行了沿坝基面的抗滑稳定分析。
2.1 刚体极限平衡法
采用的抗剪断公式[3],即公式(1):
K'=■(1)
对于折面阶梯状建基面的重力坝岸坡坝段,空间结构复杂,目前计算方法大致分为2种:一种是认为岸坡坝段产生滑动的条件是将台阶部分的混凝土或基岩剪断,与斜坡部分的建基面贯通形成滑动面,按公式(1)计算抗滑稳定;另一种是引入条分法和重力坝深层抗滑稳定分析方法,将坝体视为由若干刚性条块组成,考虑滑动条块和阻滑条块的相互作用按抗剪断公式计算抗滑稳定。本文采用第二种方法进行计算,选取6#坝块,计算简图如图2所示。
图2中,G为坝体自重,P为静水压力,U为扬压力。其中,面1-2-3-4和面5-6-7-8为横缝,9-10-11-12为刚性块体分割面。假设面3-4-11-12被剪断产生滑动,则整个结构由一个滑动体(1-2-3-4和9-10-11-12之间的块体,包括面3-4-11-12上部的岩体)和一个阻滑体(9-10-11-12和5-6-7-8之间的块体)组成,考虑滑动体和阻滑体之间的相互作用,在两者分界面(9-10-11-12)引入一个与水平面成ψ角的内力R,分别令滑动体和阻滑体这2个块体处于极限平衡状态,采用重力坝双斜面深层抗滑稳定等安全系数法的分析思路,分别列出上述2个块体的抗滑稳定安全系数K1与K2的计算式,然后令K1=K2,解出内力R,再将其代回原计算式,即可求出整个滑移体的抗滑稳定安全系数。
2.2 有限元法
在应用有限元法进行重力坝沿建基面的抗滑稳定分析的发展历程中,共出现了点安全系数法、抗滑富裕系数法、超载安全系数法和强度储备安全系数法这几种分析方法。
2.2.1 点安全系数法
计算公式如下:
Kc=■(2)
公式(2)表示正应力与剪应力的比值关系,考虑了滑动面上每个点的应力情况和基岩与上部结构相对变形对抗滑稳定的影响。点安全系数法的控制标准为如果滑动面上每个点的安全系数Kc≥1,则整个滑动面的抗滑稳定是安全的。
2.2.2 抗滑富裕系数法
计算公式如下:
Ks=■(3)
公式(3)与公式(2)在形式上基本一样,但本质上差异较大。公式(3)考虑了滑动面上的实际应力分布,在理论上更为合理。对于坝基岩体,由于不可能相当精确地弄清地质结构面的分布和岩体初始应力状态,因此坝基稳定分析以应用整体破坏准则较为合适[4]。抗滑富裕系数的判别标准与刚体极限平衡法公式(1)相同。
2.2.3 超载安全系数法
在研究大坝的安全稳定时,必须考虑一定的超载能力,主要是因为作用在大坝上的荷载和荷载组合具有许多不确定的因素。对于起挡水作用的大坝来说,如果排水失效,扬压力可能超载,上游水位也可能出现一定幅度的超载。超载安全系数法常见的有2种:超水容重法和超水位法[5]。
对于物理模型试验,往往是通过加大容重来代表水压力超载,这显然缺乏物理含义;但如果进行水位超载,合力作用点会不断变化,很快超出坝基三分点之外,使坝踵拉坏。超载方法使坝踵应力条件迅速恶化,而混凝土和基岩抗拉强度又很低,因此在数值上追求过高的超载安全度既无实际意义,又很难实现。计算超载系数时,每次增加的荷载为某一组合荷载的一个百分数,进行非线性迭代计算,直至收敛,然后施加下一个增量步(开始超载时的增量步可大一些,临界失稳时要小一点),直到计算不能收敛或者变位达到不允许的程度,从而确定超载系数Kp。
2.2.4 强度储备安全系数法
认为大坝破坏,主要是混凝土和基岩的强度随时间逐渐降低,或原先估计过高而导致大坝破坏。对于抗滑稳定问题,导致滑动失稳的主要原因是滑动面上f值和c值的降低。研究表明,在一般情况下,坝基在坝踵处基岩和胶结面存在屈服区,随着强度的降低,坝趾处胶结面出现局部区域的剪切屈服,且其扩展最初是缓慢的,随着材料强度的进一步降低,屈服逐渐加快且向上游延伸,最后与上游屈服区贯通形成滑动通道,从而导致大坝整体失稳。可将建基面屈服区贯通率作为判别整体稳定的标准[6]。
上述几种方法有各自的优缺点,近年来工程界越来越趋向于使用强度储备安全系数法作为有限元法计算混凝土重力坝沿建基面的抗滑稳定分析方法。水利行业标准《混凝土重力坝设计规范》(SL 319—2005)只规定了有限元法计算坝体(包括坝踵和坝趾)应力的判别标准,而对于使用有限元法计算坝体沿建基面的抗滑稳定,则没有规定分析方法及判别標准。能源行业标准《混凝土重力坝设计规范》(NB/T35026—2014)(代替DL5108—1999)规定:“采用弹塑性有限元法分析坝基面的抗滑稳定时,可以建基面屈服区贯通率作为控制标准”“在建基面屈服区全部贯通时,要求强度储备系数大于2.2。”
本文采用强度储备安全系数法对坝体沿建基面的抗滑稳定进行弹塑性有限元计算分析,且采用《混凝土重力坝设计规范》(NB/T 35026—2014)规定的判别标准。
3 计算过程及结果
本文以设计洪水工况为例进行重力坝岸坡坝段的抗滑稳定计算分析。施加的荷载主要有静水压力、扬压力及坝体自重。其中,上游设计洪水位为918.14 m,相应的坝下游水位为889.75 m,扬压力折减系数按《混凝土重力坝设计规范》(SL 319—2005)的规定:岸坡坝段取0.35。
3.1 刚体极限平衡法计算过程及结果
坝基面抗剪断参数为f '=0.7,c'=0.55 MPa,岩体抗剪断参数为f '=0.7,c'=0.6 MPa。利用公式(1)计算抗滑稳定安全系数,得k'=3.3>3.0,满足《混凝土重力坝设计规范》(SL319—2005)规定的要求。
3.2 有限元法计算过程及结果
3.2.1 计算模型
对计算模型采用非线性弹塑性分析,网格采用8节点六面体单元。模型计算范围选取如下:坝基上、下游各取2倍坝高作为边界,坝基深度也取2倍坝高作为模型下边界。计算模型有限元网格划分如图3所示。
3.2.2 计算参数
混凝土和基岩材料参数表见表1。
3.2.3 计算结果
分别计算了强度未降低和强度降低至储备系数等于2.2时的工况(如图4和图5所示)。
从图5可以看出,当滑动面上的f值和c值降低至储备系数等于2.2时,建基面屈服区尚未贯通,因此强度储备安全系数大于2.2,满足《混凝土重力坝设计规范》(NB/T 35026—2014)规定的要求。
3.2.4 计算结果对比分析
经过以上计算可以得出如下结论:由刚体极限平衡法计算得出的抗滑稳定安全系数和由有限元法计算得出的安全系数均能满足规范的要求,说明用上述2种方法计算重力坝岸坡坝段的抗滑稳定性都是可行的,计算结果都是可靠的;同时,计算结果也表明2种方法并未显示出哪一种更安全、更偏于保守,而是在符合规范要求的安全系数裕度上趋于一致性。
4 结语
(1)以西部某水利工程为例,分别利用刚体极限平衡法和有限元法计算重力坝岸坡坝段沿坝基面的抗滑稳定,2种方法计算得出的安全系数均符合规范要求,计算结果可靠。
(2)2种方法计算结果的安全裕度相当,并未表明哪一种更安全、更偏于保守。
(3)刚体极限平衡法计算速度快,而有限元法耗时要比刚体极限平衡法多很多,但有限元法能可视化显示坝基面塑性区的分布情况,结果更加直观,2种方法各有优缺点。当小型工程设计周期短需要追求计算速度的条件下,可优先使用刚体极限平衡法。
参 考 文 献
[1]林继镛.水工建筑物[M].第5版.北京:中国水利水电出版社,2008:47-49.
[2]韦山红.基于ANSYS的重力坝应力分析[J].企业科技与发展,2013(13):128.
[3]SL 319—2005,混凝土重力坝设计规范[S].
[4]刘亚丽,辛全才.基于ANSYS的滚水坝稳定与应力分析[J].水资源与水工程学报,2011,22(1):119.
[5]郭建业.混凝土重力坝抗滑稳定及应力控制标准研究
[D].大连:大连理工大学,2007:29-30.
[6]NB/T 35026—2014,混凝土重力坝设计规范[S].
[责任编辑:陈泽琦]
