基于Saber的舵机采样处理电路设计与仿真分析
2017-05-30徐晓璐张昆峰
徐晓璐 张昆峰

摘 要:针对舵机伺服控制系统高可靠性和高精度的设计指标,本文设计了一种基于旋转电位器的舵偏角采样处理电路,设计过程中利用Saber软件搭建了所设计电路的仿真模型,分析了元器件参数偏差对电路性能的影响,进而完成了关键元器件的参数设计。通过功能、时域性能分析和蒙特卡洛仿真分析,验证了设计的采样处理电路的可行性、高可靠性和高精度性。
关键词:采样处理电路;电位器;Saber软件
引言
数字舵机伺服系统作为一种高精度的机电一体化装置,是操纵飞行器机动飞行的重要机构,其工作原理是:控制单元同时接收来自上位机的指令,以及由反馈回路采集的输出轴位置信息,通过比较实际输出与期望输出,产生控制指令,驱动输出轴达到指定的位置,整个控制过程是一个闭合的回路,可以达到高精度控制的目的。
在伺服系统中,反馈回路是一个重要环节,它的性能将直接影响伺服系统的控制精度。反馈回路主要包括两部分:机械传动机构和采样处理电路,而影响系统性能的主要因素都在于采样处理电路中。本文针对以角位置为输出量的数字舵机系统,设计了基于旋转电位器的采样处理电路,利用Saber软件建立了它的仿真分析模型,对电路进行了灵敏度分析,找出了影响性能的关键参数,并以此为基础设计了各元器件的误差等级。针对选用误差等级的元器件,分析了电路的输出特性,验证了电路设计与元器件选型的可行性,为伺服系统反馈回路的设计和改进提供了参考。
1 系统原理设计
本文利用旋转电位器将系统输出端的位置信息转换为电平信号,并对电平信号进行滤波,以剔除杂波干扰,滤波后的信号输入到跟随器进行电压跟随,最后利用A/D转换器将电平信号转换为数字量,供控制单元计算使用,即设计的采样处理电路的工作原理如图1所示。
图1中,Input表示舵机系统输出轴的角位置,Posmeter表示电位器,P15和N15分别表示电位器的正、负供电电压,POS表示跟随器的输出电压,该电平信号传入A/D转换器并被转换为对应的数字量,之后传入控制单元,供解算控制指令使用。
考虑到舵机系统传动机构的设计(系统输出轴的机械限位为-34°~34°,输出轴到旋转电位器的传动增速比为4),A/D转换器选用TLC2574精密数模转换器(工作区间为-10V~+10V),旋转电位器选用总阻值为4.7kΩ,有效电行程为300°的精密电位器,电位器供电模块输出电压为+15V和-15V;选用LM148跟随器进行电压跟随;为了将跟随器输出端Pos的电压调整到A/D转换器的允许输入范围之内,需将正负供电电源各串联一个953Ω的电阻后再接到电位器供电端;低通滤波电路的时间常数为0.1ms(电阻值为10kΩ,电容值为0.01μF)。
至此,我们得到了初步设计的采样处理电路。
2系统原理验证
判定设计的采样/处理电路的合理性的最低要求是:元器件参数值在标称情况下,当输出轴在极限位置时,控制单元接收的输出轴位置信息无失真,即跟随器的输出值始终在A/D转换器正常工作范围之内。因此,主要的考察点就是极限位置下跟随器输出的电压值。
给采样处理电路原理模型分别输入±34°的信号,可以得到元器件参数标称情况下的输出端POS电压值:34°对应9.6750V,0°对应0V,-34°对应-9.6737V。
在标称情况下,跟随器的输出电压范围在-10~10V范围内,该仿真结果表明采样/处理电路符合最低设计要求,即设计的采样处理电路在原理上是可行的。
在实际应用中,元器件的参数与设计值存在一定的偏差,参数偏差区间越小意味着更高的系统精度和更高的成本。因此,选用合适等级的元器件也是电路设计中的重要工作。为此,我们需要对电路进行灵敏度分析,进而寻找影响系统性能的关键参数并确定相应的误差等级。
3系统灵敏度分析与关键参数确定
由工作原理图1可以知道,元器件参数偏差的综合作用,可能会导致跟随器的输出电压波动并超出A/D转换器的允许输入范围,故以输出端POS电压值为目标变量,对其值进行灵敏度分析。
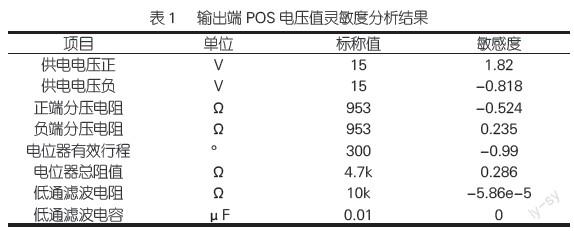
利用Saber软件,搭建包含电位器、供电模块、分压电阻和滤波电路的详细仿真模型如图2所示,通过分析,得到跟随器输出端POS的灵敏度分析结果如表1中所示。
从表1中可以看出,供电模块的正、负供电电压和电位器有效电行程对跟随器输出电压影响最大,分压电阻和电位器总阻值的影响次之,低通滤波器的电阻和电容对其几乎无影响。
根据灵敏度分析结果,综合考虑设计指标与使用需求,选用如下所述误差等级的元器件:
电位器总电阻误差等级为±10%,有效电行程误差等级为±1%;电位器分压电阻器误差精度等级为:±0.1%;供电模块+15V输出误差精度等级为±1%,-15V输出误差等级为±2%;低通滤波网络的电阻误差等级为±2%,电容误差等级为±10%。
从表1中可以看出,供电模块的正、负供电电压和电位器有效电行程对跟隨器输出电压影响最大,分压电阻和电位器总阻值的影响次之,低通滤波器的电阻和电容对其几乎无影响。
根据灵敏度分析结果,综合考虑设计指标与使用需求,选用如下所述误差等级的元器件:
电位器总电阻误差等级为±10%,有效电行程误差等级为±1%;电位器分压电阻器误差精度等级为:±0.1%;供电模块+15V输出误差精度等级为±1%,-15V输出误差等级为±2%;低通滤波网络的电阻误差等级为±2%,电容误差等级为±10%。
4采样处理电路蒙特卡罗分析
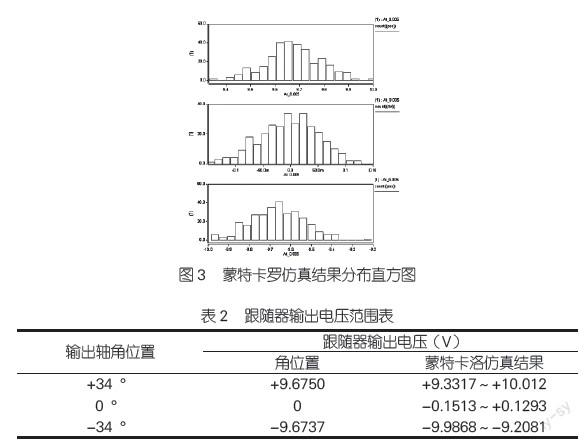
为了验证选用元器件的合理性,利用蒙特卡罗法对正、负极限位置和零位分别进行仿真,抽样仿真次数各为300次,仿真结果如图3所示,由上至下分别为反馈回路输入指令分别为34°、0°、-34°时的结果分布。
由图3可以看出,当舵机系统输出轴在34°、0°、-34°位置时,跟随器输出端POS的电压值以相应的标称值为中心散布,散布趋势呈正态分布,输出电压散布范围如表2第3列所示。
由表2可以看出舵机伺服系统工作在极限位置时,在元器件参数偏差的综合作用下,输出端POS的值基本都位于±10V以内,极小概率会出现高于10V的情况(高于10V的仿真情形为2次,不到总数的1%),且超差量也很小,仅有0.012V。
在实际当中,元器件的参数同时处于允许误差的边界的概率非常低;此外,伺服系统在工作中,上位机给出的指令信号都不会达到极限工作位置,因此并不会出现电压值超出A/D转换器工作区间的情况,足以保证控制单元接收到线性变化的角位置信息,因此,设计的采样处理电路可以满足无失真的反应输出轴的位置信息的需求。
如果要确保在任何情况下,A/D转换器都能保持线性输出,可以增大电位器两端的分压电阻,或者选用更高精度等级的元器件,减小参数的离散区间,从而达到限制跟随器输出电压幅值的目的。
5结语
本文根据伺服系统的使用需求,设计了一种基于旋转电位器的位置采样处理电路,进而利用Saber对电路进行灵敏度分析,确定了不同元器件参数对电路输出的影响程度,并以此为依据选定了合适误差等级的元器件。
接着,本文对设计的电路进行了蒙特卡洛仿真,从仿真结果可以看出,选用误差等级的元器件既充分利用了A/D转换器的工作范围,又避免了在正常工作情况下A/D转换器出现饱和的情况。因此,设计的采样处理电路可以满足伺服系统高可靠性、高精度控制的需求。
参考文献
[1]赵小龙,马铁华,刘艳莉.一种数字化舵机系统设计与实现[J]. 核电子学与探测技术,2012,32(5):552-555.
[2]吴称列.基于DSP的无刷直流电机舵机系统的设计与研究[D].湘潭大学,2015.
