全浮式半轴的结构计算分析与优化设计

吴磊 梁卓 林圣存 沈光烈

摘 要：根据力学公式及有限元线性计算的结果得出委托方提供的全浮式半轴原始设计具备了结构优化条件；结合产品新工艺提出了3种优化方案，分别对各种设计方案在考虑材料非线性和结构表面热处理因素影响的条件下进行非线性有限元分析；使用失效扭矩作为评价各设计方案的强度指标，结合减重效率值对各设计方案进行比较；采用该方法所得出的最优设计方案不仅简化了产品加工工艺而且具有显著的减重效果.

关键词：全浮式半轴；优化；有限元；非线性；强度

中图分类号：U463.218.6 文献标志码：A

0 引言

目前，车辆上所使用的半轴多数为实心转轴结构[1]，然而，作为全浮式半轴因为具有只承受扭矩而不承受弯曲的特点[2]，根据圆轴纯扭转时横截面的剪应力分布特点可知：截面上剪应力的大小与该位置到圆心位置的距离成正比；所以，远离圆心位置的外表面剪应力最大而截面圆心处剪应力为零.因此，鉴于半轴心部材料的承载效率十分低下，可以将半轴设计成空心结构.空心结构的设计方案相对于实心结构除了具有减轻结构重量降低材料使用量的优点外，更为重要的是可以优化产品加工工艺：传统的实心半轴所采用的加工工艺如下：下料、锻造、热处理、校直、粗加工、半精加工、铣齿、热处理、校直、精加工[3]，如果半轴采用空心结构则可采用无缝管材通过摩擦焊接的方式与法兰盘以及花键轴连接，省去繁琐的车削加工和校直工序，同时也不需要大型的车削机床，即可降低加工成本也可提高生产效率.研发出强度能够满足设计要求的空心结构的半轴将会给企业带来巨大的经济效益，也是本研究的重点.

研究通过简单的力学公式计算和有限元线性计算判断该结構是否具备结构优化的条件，对各优化设计方案在考虑材料非线性和表面热处理下采用非线性计算方法进行更加复杂的有限元分析.此外，通过在有限元模型中加入材料非线性和结构表面热处理两个复杂因素，得到结构强度评价指标——失效扭矩，计算出了各优化方案相对原始方案的强度降低率.通过对各优化设计方案的强度降低率和减重效率综合评价，能够直观地评选出最优优化方案.

1 结构优化可行性分析

委托方提供了全浮式半轴原始设计模型（如图1所示）：半轴为外径（D）62 mm，长度1 013 mm；设计扭矩（T设计）为30 000 N·m，破坏扭矩（T破坏）为67 500 N·m.

为研究结构优化的可行性，分别通过力学公式和有限元线性静态计算，得出该实心结构外表面最大剪应力值，并对两种计算结果的对比来验证计算方法的正确性.

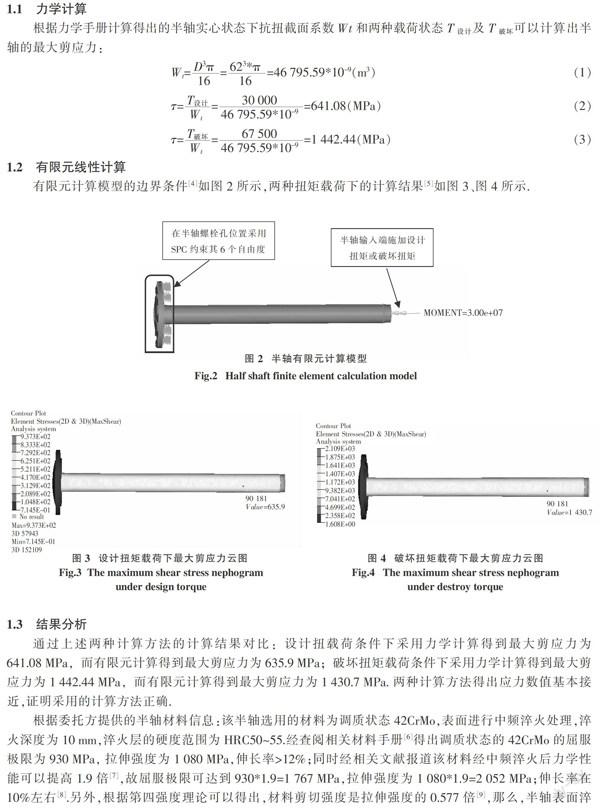
1.1 力学计算

1.2 有限元线性计算

有限元计算模型的边界条件[4]如图2所示，两种扭矩载荷下的计算结果[5]如图3、图4所示.

1.3 结果分析

通过上述两种计算方法的计算结果对比：设计扭载荷条件下采用力学计算得到最大剪应力为641.08 MPa，而有限元计算得到最大剪应力为635.9 MPa；破坏扭矩载荷条件下采用力学计算得到最大剪应力为1 442.44 MPa，而有限元计算得到最大剪应力为1 430.7 MPa. 两种计算方法得出应力数值基本接近，证明采用的计算方法正确.

根据委托方提供的半轴材料信息：该半轴选用的材料为调质状态42CrMo，表面进行中频淬火处理，淬火深度为10 mm，淬火层的硬度范围为HRC50～55.经查阅相关材料手册[6]得出调质状态的42CrMo的屈服极限为930 MPa， 拉伸强度为1 080 MPa，伸长率>12%；同时经相关文献报道该材料经中频淬火后力学性能可以提高1.9倍[7]，故屈服极限可达到930*1.9=1 767 MPa，拉伸强度为1 080*1.9=2 052 MPa；伸长率在10%左右[8].另外，根据第四强度理论可以得出，材料剪切强度是拉伸强度的0.577倍[9]，那么，半轴表面淬火层的剪切强度极限为2 052*0.577=1 184 MPa，心部调质层的剪切强度极限为1 080*0.577=623 MPa.根据半轴原始结构强度校核发现：该设计状态完全满足设计所需的强度要求且存在较大的优化空间；因此，具备结构优化的前提条件.

2 结构优化设计与分析

2.1 设计方案的提出

结合产品新工艺要求，本次研究的设计方案是在保持半轴原外径不变的情况下，根据半轴内径的大小分为以下3种优化方案：

方案一：半轴内径为20 mm

方案二：半轴内径为30 mm

方案三：半轴内径为40 mm

通过有限元计算对以上3种优化方案进行强度校核.由于原始方案在破坏扭矩载荷条件下，该结构最大剪应力为1 430.7 MPa超过了材料相应状态的剪切强度极限1 184.0 MPa，所以为了更加准确地反映结构的强度情况，此次结构优化分析中将考虑材料非线性因素的影响，并且将结构的表面热处理部分和心部分别赋予具有相应屈服极限和强度极限的材料如图5所示.

2.2 非线性计算模型化说明

本次非线性分析选用ABAQUS软件，为了更加精确地反映半轴横截面内应力的变化，网格类型设定为边长1 mm的六面体[10].由于半轴纵向同一半径位置应力相等，为提高计算效率，只截取半轴纵向长度为40 mm的一段进行有限元计算，具体计算模型如图6所示.

两种材料的应力应变简化曲线如图7和图8所示.

2.3 计算结果

分别对原始设计结构和3种优化方案按照上述建模方法进行计算，以计算过程中的失效扭矩作为各种设计方案的强度评价指标.

2.3.1 原始设计结构计算结果

通过图9和图10的应力云图分析发现：计算终止时刻半轴整个中频淬火层应力在1 180 MPa以上达到了中频淬火的剪切强度极限，同时调质层外侧应力623 MPa也达到了调质材料的剪切强度极限，可以确定结构失效导致了计算终止.通过计算得出终止时刻的加载扭矩为破坏扭矩的92.9%（62 100 N·m），将该时刻的加载扭矩称之为失效扭矩.失效状态下的结构剪应力云图如图9和图10所示.

2.3.2 优化方案一计算结果

由于半轴挖去了心部直径为20 mm部分，使结构强度得到一定的削弱，扭矩加载到破坏扭矩的90%（60 750 N·m）时，半轴整个中频淬火层剪应力都达到了剪切强度极限，导致计算终止，失效状态下的结构剪应力云图如图11和图12所示.

2.3.3 优化方案二计算结果

该设计状态下，结构强度得到进一步削弱，扭矩加载到破坏扭矩的85.9%（57 982 N·m）半轴出现结构失效导致计算终止，失效状态下的结构剪应力云图如图13和图14所示.

2.3.4 优化方案三计算结果

该设计状态下，扭矩加载到破坏扭矩的77.6%（52 380 N·m）半轴出现结构失效计算终止，失效状态下的结构剪应力云图如图15和图16所示.

2.4 结果分析

3 结论

通过上述3种优化方案分析结果对比得出：优化方案二的强度降低率只有6.631%而减重效率达到了23.413%，综合指标最理想；因此，建议委托方首先考虑参照优化方案二即外径62 mm内径30 mm的设计方案进行产品设计.

參考文献

[1] 陈家瑞.汽车构造（下册）[M]. 2版.北京：机械工业出版社，2005.

[2] 林幕义，张福生.车辆底盘构造与设计[M].北京：冶金工业出版社，2007.

[3] 李聚群，左传付，耿伟，等.汽车后桥半轴的数控车削加工[J].金属加工，2008（3）：65-66.

[4] 吴磊，梁卓，沈光烈，等.双联式万向节有限元分析及结构改进[J].广西科技大学学报，2016，27（3）：65-68.

[5] 王祖皓，尹辉俊，张芸华，等.某叉车门架有限元模型评估[J].广西科技大学学报，2015，26（4）：21-22.

[6] 梁耀能.机械工程材料[M].广州：华南理工大学出版社，2007.

[7] 周成，卢曦，焦玉强.中频淬火在传动轴轻量化上的应用[J].热加工工艺，2014，43（2）：181-183.

[8] 姚贵升，景立媛.汽车用钢应用技术[M].北京：机械工业出版社，2007.

[9] 刘鸿文.材料力学[M].北京：高等教育出版社，2004.

[10] 赵腾伦.ABAQUS 6.6在机械工程中的应用[M].北京：中国水利水电出版社，2007.

Abstract：First， the original design of a full-floating axle shaft entrusted by the client has the condition of structure optimization based on mechanical formula and the finite element linear calculation. Then， we put forward three optimal schemes and conduct nonlinear finite element analysis respectively after considering nonlinear material and structural heat treatment. Finally， we innovatively use failure torque as the strength index to evaluate the schemes. And we also consider weight loss efficiency value in evaluating the schemes. The optimal design scheme not only simplifies the product processing craft but also has significant effect of weight loss， thus has gained recognition of the client.

Key words：axle shaft； optimization； finite element； nonlinear； strength

（学科编辑：黎 娅）