基于PSO—LDA的人脸识别算法

王鹏涛 王智文

摘 要：线性判别分析（LDA）方法在人脸识别特征提取中应用广泛.针对其在应用方面存在的缺陷，本文提出一种基于粒子群优化（PSO）的LDA算法（PSO-LDA）的人脸识别算法.通过粒子群优化算法找寻到矩阵的最佳投影矢量，避免了直接对矩阵求特征值和特征向量，并通过多次迭代来解决投影空间中边缘类相近样本重叠问题.在ORL库中进行对比实验，实验结果表明提出的方法抗噪性能好，能明显提高人脸识别率.該算法具有识别稳定和便于实现的特点.

关键词：线性判别分析；粒子群算法；最佳投影矢量；PSO-LDA

中图分类号：TP317.4 文献标志码：A

0 引言

人脸识别是生物特征识别的一种，也是模式识别等领域中的前沿研究课题，因为其具有直接性，非接触性，方便友好等特点，在铁路、公安、银行等众多领域得到了广泛的研究[1-2].目前，数字图像处理技术在实际应用中广泛使用[3]，人脸识别越来越成为当前模式识别和人工智能领域的一个研究热点[4].线性判别分析（LDA）方法作为一种经典的特征提取算法，由于其对光照、表情、姿态的敏感度较低，因而在人脸识别中得到广泛使用[5].但在使用LDA算法时会遇到两个方面的问题：1）求解复杂协方差矩阵的特征值和特征向量时，会遇到矩阵不可解的情况；2）存在边缘类，使得投影空间中的相近样本重叠的问题.针对这两方面的缺陷，本文提出了一种基于粒子群优化（PSO）的LDA算法（PSO-LDA），用粒子群优化算法求矩阵的最佳投影矢量，避免了直接对矩阵求特征值和特征向量，通过多次迭代求解能很好地避免边缘类问题.

1 相关理论

人脸识别方面的相关理论比较多，本文仅就经典的人脸特征提取算法的线性判别分析方法进行简单介绍，并介绍用于优化该算法的粒子群优化算法.

1.1 传统LDA算法简介

线性判别分析（Linear Discriminant Analysis，LDA）是模式识别的经典算法之一[6].线性判别分析方法的基本思想是将高维模式样本投影到最佳鉴别矢量空间，以达到抽取分类信息和压缩特征空间维数的目的，使投影后的模式样本在新的子空间中有最大的类间距离和最小的类内距离[7-8]，即选择使类间与类内离散度矩阵比值最大的特征来保证样本数据在投影空间中有最佳的可分离性[9-10].分别用式（1）、式（2）和式（3）来定义类间离散度矩阵SB，类内离散度矩阵SW和目标函数Ja.

1.2 粒子群优化算法简介

粒子群优化算法（Particle Swarm Optimization，PSO），是源于Kennedy博士和Eberhart博士对鸟群觅食的研究提出的进化算法[12]，其中，首次研究是为了解决连续条件下的优化问题，随着越来越多的问题出现在离散空间，粒子群的研究方向也朝着这方面转变[13].鸟类在觅食时，每只鸟都不是直接去寻找食物，而是通过寻找距食物最近的鸟来进行下一步搜寻.因此，随机产生一组粒子，每个粒子对应一个适应度的值，该值由适应度函数决定，而适应度函数用速度、位置和适应度的值来表征该粒子特征[14-16].算法通过式（4）和式（5）来进行速度更新和位置更新[17].

其中，为惯性权重，表示粒子对自身速度的记忆程度，在PSO算法中一般设为[0.3，1.2]之间的一个常数，r1，r2取区间[0，1]的随机数，c1，c2是加速因子，为非负整数，c1是粒子跟踪自己历史最优值的权重系数，它表示粒子自身的认知，所以叫“自我认知”；c2是粒子跟踪群体最优值的权重系数，它表示粒子对整个群体知识的认识，所以叫做“社会认知”，通常取c1=c2=1.494 45[18-19].pbest为个体极值，gbest为整个粒子群的全局极值，Xk记录第k个粒子的当前位置，Vk记录第k个粒子的当前速度，为了控制粒子因随意乱跑而超出搜寻范围，通常对粒子设置一个限度，Xk大小在[-xmax，xmax]，Vk大小设置在[-vmax，vmax].当目标函数误差达到要求或者迭代次数到达上限则算法终止.

进一步研究表明，惯性权重因子值与全局寻优能力成正比.值较大则全局寻优能力强，反之则全局寻优能力弱.但是，对于迭代算法而言，作为常数值引入到粒子群优化算法之中并不能很好地增强算法的全局寻优能力.为了得到更优的全局寻优能力同时又得到相对较小的惯性权重因子，故而惯性权重因子的取值方式得到了有效改进，其惯性权重因子转变为动态值，用式（6）来计算.

式（6）中，t为当前的迭代次数，tmax为最大的迭代次数，（t）则代表了惯性权重因子在第t次迭代的值，t0是惯性权重的最初值，而tn则是惯性权重的最终值.

惯性权重因子（t）的引入使得标准粒子群优化算法在收敛的稳定性上得到了很大改善，经过大量的数据演算与近20年的技术融合，惯性权重因子（t）的取值从0.9递减到0.4可以使得粒子群优化算法拥有较好的性能.惯性权重因子（t）对粒子群优化算法稳定性收敛的结果，使得粒子群优化算法成功地运用到了诸多实际问题的解决方案之中.

2 提出的PSO-LDA算法

Step1 初始化一簇粒子.根据数据复杂程度，设定迭代次数genmax=50，粒子群规模popsize=30，随机位置Xk∈[-1，1]和随机速度Vk=[-2，2].值得注意的是，粒子群优化算法中粒子的位置，为LDA算法的核心：投影矩阵A.因此，在设置投影矩阵大小时，需要考虑待优化矩阵，假设待优化的数据大小为n×m，其中m为样本个数，n是样本维数，为了达到降维的目的，就需要一个大小为d×m的投影矩阵，其中dStep3 对每个粒子，将其适应值与其经过的最好位置pbest作比较，如果较好，则将其作为当前的最好位置pbest.

Step4 对每个粒子，将其适应值与其经过的最好位置gbest作比较，如果较好，则将其作为当前的最好位置gbest.

Step5 根据式（4）、式（5）调整粒子速度和位置.若粒子陷入局部最优，返回Step 1.

Step6 未达到结束条件则转Step 2.

Step7 迭代终止，即达到最大迭代次数.

3 仿真实验结果及分析

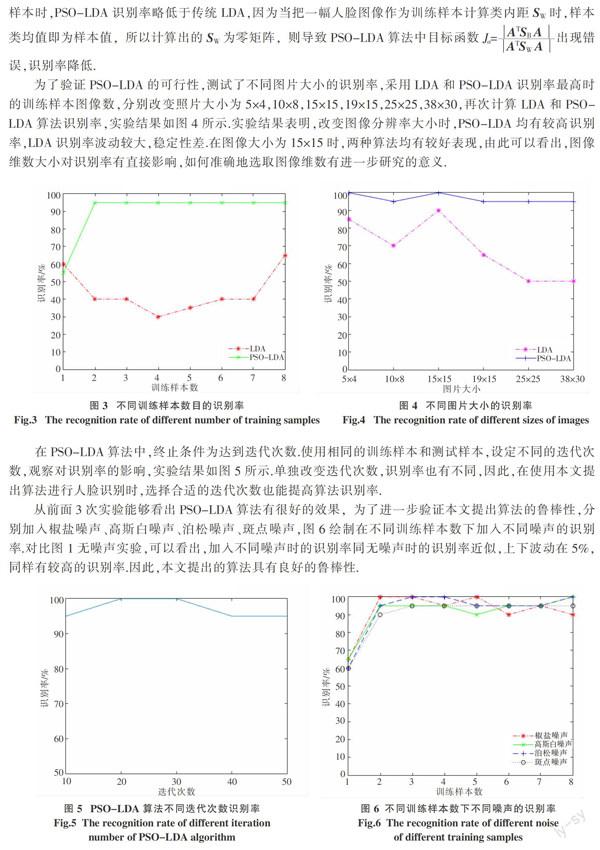
本文使用ORL数据库进行实验，该库中共有40个不同性别、不同年龄的对象，每个对象10幅人脸图像，共计400幅图像，大小為112×92，256个灰度级，其中，每个对象的人脸表情和姿态均有变化，包括笑、不笑，戴眼镜、不带眼镜等.图2选取了ORL数据库中部分人脸图像[20].实验时，为提高识别速度，图片大小压缩为19×15，将后2幅图像作为测试样本，其余8幅图像作为训练样本，计算传统LDA算法和PSO-LDA算法识别率.然后将训练样本逐次递减，测试样本不变，重新计算识别率.LDA和PSO-LDA识别率如图3所示.从图3可以看出不同训练样本数目下，PSO-LDA识别率均值远远大于LDA识别率，LDA平均识别率为36.25%，PSO-LDA平均识别率为94%.随着训练样本数目的增加PSO-LDA识别率基本稳定，而传统LDA算法识别率却波动较大，可以看出提出算法对小样本问题有所改善.但当只将一幅人脸图像作为训练样本时，PSO-LDA识别率略低于传统LDA，因为当把一幅人脸图像作为训练样本计算类内距SW时，样本类均值即为样本值，所以计算出的SW为零矩阵，则导致PSO-LDA算法中目标函数出现错误，识别率降低.

为了验证PSO-LDA的可行性，测试了不同图片大小的识别率，采用LDA和PSO-LDA识别率最高时的训练样本图像数，分别改变照片大小为5×4，10×8，15×15，19×15，25×25，38×30，再次计算LDA和PSO-LDA算法识别率，实验结果如图4所示.实验结果表明，改变图像分辨率大小时，PSO-LDA均有较高识别率，LDA识别率波动较大，稳定性差.在图像大小为15×15时，两种算法均有较好表现，由此可以看出，图像维数大小对识别率有直接影响，如何准确地选取图像维数有进一步研究的意义.

在PSO-LDA算法中，终止条件为达到迭代次数.使用相同的训练样本和测试样本，设定不同的迭代次数，观察对识别率的影响，实验结果如图5所示.单独改变迭代次数，识别率也有不同，因此，在使用本文提出算法进行人脸识别时，选择合适的迭代次数也能提高算法识别率.

从前面3次实验能够看出PSO-LDA算法有很好的效果，为了进一步验证本文提出算法的鲁棒性，分别加入椒盐噪声、高斯白噪声、泊松噪声、斑点噪声，图6绘制在不同训练样本数下加入不同噪声的识别率.对比图1无噪声实验，可以看出，加入不同噪声时的识别率同无噪声时的识别率近似，上下波动在5%，同样有较高的识别率.因此，本文提出的算法具有良好的鲁棒性.

从4次实验结果来看，本文提出的PSO-LDA算法在ORL数据库上的表现均优于传统LDA算法，不仅在识别率上有很大提高，而且有良好的鲁棒性.

4 结语

本文通过介绍传统LDA算法和PSO算法，并将两者结合提出PSO-LDA算法.通过PSO算法求解LDA中的投影矩阵，改善了LDA算法的小样本识别率，解决了传统LDA中复杂繁琐的协方差矩阵的求解问题，同时体现出PSO-LDA的方便、快捷，而且在识别效果上看识别率得到了明显提高，有良好的鲁棒性并且稳定.实验结果表明，这种算法在人脸识别方面表现优良，而且通过研究也提出更高的要求，如何选择合适的图像大小和迭代次数使识别率再提高成为今后研究的重点.

参考文献

[1] ZHOU C J，WANG L，ZHANG Q，et al. Face recognition based on PCA image reconstruction and LDA[J]. Optik-International Journal for Light and Electron Optics，2013，124（22） ： 5599-5603.

[2] MARVADI D，PAUNWALA C，JOSHI M，et al. Comparative analysis of 3D face recognition using 2D-PCA and 2D-LDA approaches[C]//Proceedings 2015 5th Nirma University International Conference on Engineering，NUiCONE 2015.US：Institute of Electrical and Electronics Inc，2015.

[3] 俞昊，林川，谭光兴，等. 视觉注意机制与Canny算子结合的目标轮廓检测方法[J].广西科技大学学报， 2016，27（2）：87-92.

[4] 周德龙，高文，赵德斌. 基于奇异值分解和判别式KL投影的人脸识别[J].软件学报，2003，14（4）：783-789.

[5] 周柏清，任勇军. LDE融合光谱回归分类的光照变化人脸识别[J]. 计算机工程与应用，2014，50（11）：154-158.

[6] PASAD M M. 1D-LDA verses 2D-LDA in online hadwriting recognition[C]//2014 International Conference on Circuits，Communication，Control and Computing，IEEE ICC 2014.US：Institute of Electrical and Electronics Inc，2014.

[7] 董晓庆，陈洪财. 基于子模式行列方向二维线性判别分析特征融合的特征提取[J].计算机应用，2014，34（12）：3593-3598.

[8] BANSAL A，MEHTA K，ARORA S. Face recognition using PCA and LDA algorithm[C]//International Conference on Advanced

Computing &Communication Technologies.US：Institute of Electrical and Electronics Inc，2012.

[9] CLEMMENSEN L，HASTIE T，WITTEN D，et al. Sparse discriminant analysis[J]. Technometrics，2011，53 （4）：406-413.

[10] HASTIE T，BUJA A，TIBSHIRANI R. Penalized discriminant analysis[J].Annals of Statistics，1995，23（1）：73-102.

[11] LU G F，ZOU J，WANG Y. Incremental complete LDA for face recognition[J]. Pattern Recognition，2012，45 （7）：2510–2521.

[12] KENNEDY J，EBERHART R.Particle swarm optimization[C]//IEEE International Conference on Neural Networks，ICNN 1995.

US：Institute of Electrical and Electronics Inc，1995.

[13] AOKI T，ARANHA C，KANOH H.PSO algorithm with transition probability based on hamming distance for graph coloring problem[C]//2015 IEEE International Conference on Systems.US：Institute of Electrical and Electronics Inc.2015.

[14] 唐俊. PSO 算法原理及应用[J]. 计算机技术与发展，2010，20（2）：213-216.

[15] 张利凤.粒子群优化算法及其应用[D].重庆：重庆大学，2012.

[16] MARINI F，WALCZAK B. Particle swarm optimization（PSO）. A tutorial[J]. Chemometrics and Intelligent Laboratory Systems.

2015，149：153-165.

[17]皮倩瑛，叶洪涛.一种动态调节惯性权重的粒子群算法[J].广西科技大学学报，2016，27（3）：26-32.

[18] DADGAR M，JAFARI S，HAMZEH A. A PSO-based multi-robot cooperation method for target searching in unknown environments[J]. Neurocomputing，2016，177（C）：62-74.

[19] YAN W.Improved discrete particle swarm optimization and application in attribute reduction[D].Harbin：Harbin Engineering University，2011.

[20] ATT Laboratories Cambridge.The ORL Database of Faces[DS/OL].（2015）[2015-07-12].http：//www.cam-orl.co.uk/ facedatabase.html.

Abstract：The method of linear discriminant analysis （LDA） is widely used in feature extraction of face recognition. In view of its defects in application， a LDA face recognition algorithm based on particle swarm optimization （PSO） is proposed in this paper. The eigenvalues and eigenvectors of matrix are avoided to calculate directly by using particle swarm optimization algorithm to find the best projection vectors of matrix， and the overlapping problem of similar samples of the edge class in the projection space is solved through several iterations. Experiments are conducted using ORL face database， the results show that the proposed method has good anti-noise performance and can significantly improve the rate of face recognition. The proposed method have a better stability， and easy to realize.

Key words： linear discriminant analysis； particle swarm optimization algorithm； best projection vectors； PSO-LDA

（學科编辑：黎 娅）