从三次备课谈对“学程导航”教学理念的感悟

洪劲松

【摘要】“互动课堂，学程导航”的教学理念是现代知识教学思想改革的必然趋势。它要求教育者转变知识教学观，重新反省、审视以知识积累与储存为中心的“传授知识——接受知识”的教学模式，树立以知识的经验、能力、智慧和方法为中心的“再现知识——探索知识”的教学模式。

【关键词】建构 互动课堂 学程导航 探索

建构主义学习理论认为：学习不应被看成是对于教师所授知识的被动接受，而应是学习者以自身已有的知识和经验为基础的主动建构活动。对知识的真正理解只能是由学习者基于自己的经验背景而建构起来的，取决于特定情景下的学习过程。如此说来，“互动课堂，学程导航”的教学模式与建构主义理论有着“异曲同工”之妙。笔者以《能被3整除的数的特征》为背景，通过三次备课阐述自己对“学程导航”教学理念的感悟。

一

[教学片段]

师：上节课，我们学习了能被2、5整除的数的特征，主要是根据这个数的个位数字来加以判断，这节课我们来研究能被3整除的数的特征。首先，我们来做一个游戏，同学们任意报一个数，老师能猜出它是否能被3整除。

（学生报数，教师把能被3整除与不能被3整除的数分别写在黑板上）

6 12 135 300 471 20 55 98 460 1000

…… ……

师：两边的数，一类能被3整除，另一类不能被3整除，这其中有什么规律呢？请同学们把这些数各位上的数字加起来。（学生进行运算）

师：现在，你们有什么发现吗？

学生通过讨论、交流，发现左边各数的数字和都能被3整除，右边各数的数字和都不能被3整除，由此得出能被3整除的数的特征。

[教学反思]显然，在教学过程中，教师把着眼点放在了“能被3整除的数”的特征的获得上。一开始通过猜数活动，充分调动和激发学生的好奇心，并得到“能被3整除的”和“不能被3整除的”两组数，这样既能通过再现或再认等方式，激活学生头脑中已有的相关知识，同时又为新授知识做铺垫或者分散新课的难点。但是，由于教师铺垫或暗示过度，人为地设置了狭窄的思维通道，学生常常无需探究或稍加尝试，结论就出来了，这样的设计只关注了知识的层面，却没有深入到方法的层面。学生通过这个内容的学习，记忆和掌握的仅仅是“能被3整除的数”的特征，尽管这个特征是数学知识的组成部分，但只是边缘的、外围的或表面的。

二

[教学片段]

师：能被3整除的数的特征是什么？它与什么有关呢？今天，我们就来研究这个问题。

1. 演示。

拿出几个小圆片，在数位顺序表上各摆几个数，看看能否被3整除，并记录。

[图片个数＼&摆成的数＼&能否被3整除＼&5＼&5、23、14、41、32、50＼&不能＼&6＼&123、321、132、1014 …… ＼&能＼&]

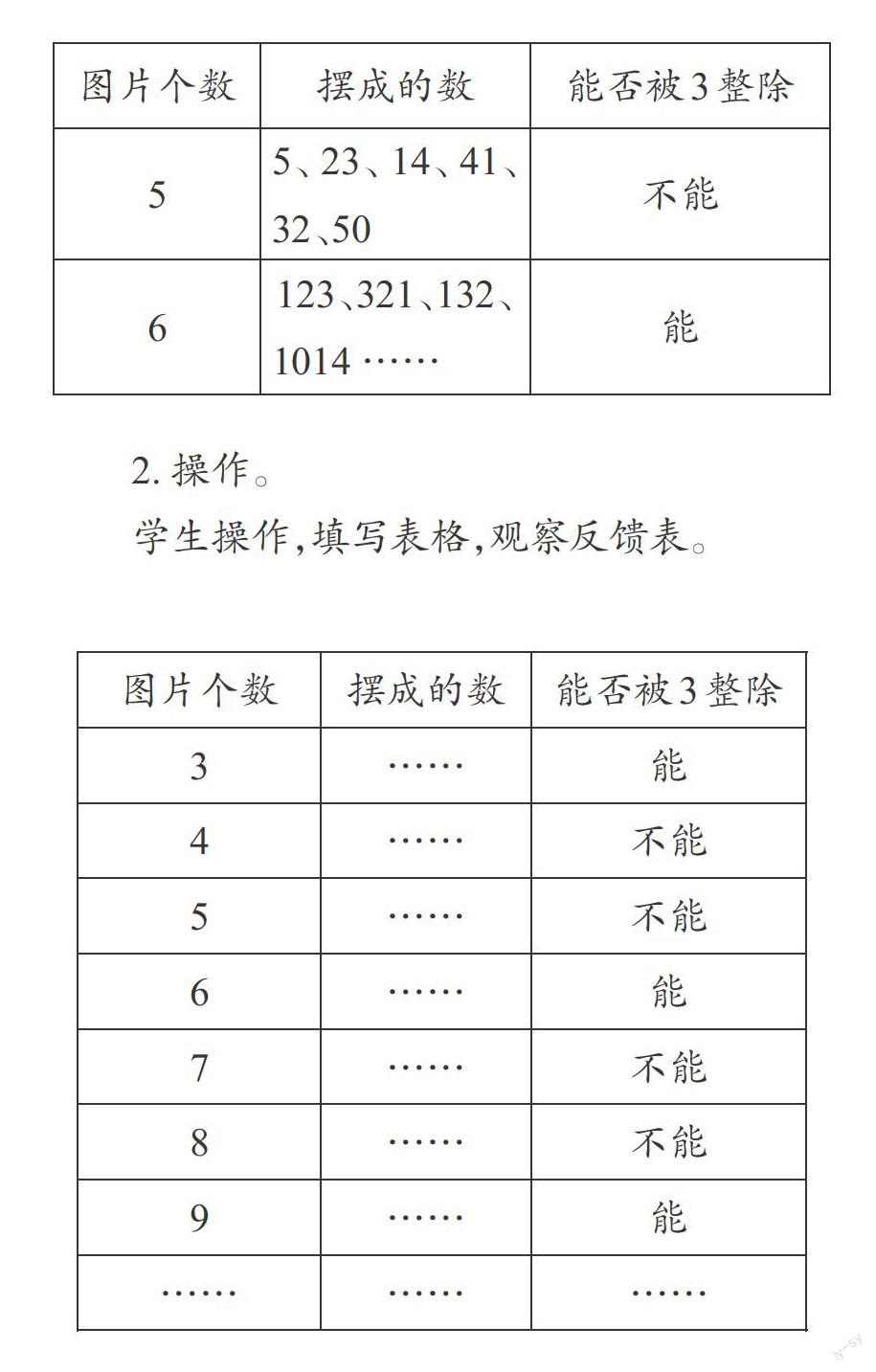
2. 操作。

学生操作，填写表格，观察反馈表。

[图片个数＼&摆成的数＼&能否被3整除＼&3＼&……＼&能＼&4＼&……＼&不能＼&5＼&……＼&不能＼&6＼&……＼&能＼&7＼&……＼&不能＼&8＼&……＼&不能＼&9＼&……＼&能＼&……＼&……＼&……＼&]

（学生发现拿4个、5个、7个、8个……圆片摆的数都不能被3整除，拿3个、6个、9个……圆片摆的数都能被3整除）

3. 思考。

能被3整除的数与什么有关？（圆片的个数还是数位顺序？）

学生发现：与圆片个数有关，与顺序无关。

4. 猜想。

用多少个圆片组成的数一定能被3整除？用多少个圆片组成的数一定不能被3整除？

5. 归纳。

能被3整除的数的特征是什么？

小结：一个数各位上数字的和能被3整除，这个数就能被3整除。

[教学反思]从某种程度上来说，这一次教学体现了思维的开放性和指向性。我开始注重知识规律的探索，试图在传授知识的同时，引导学生经历知识探究的过程。学习一种方法，感受一种思想，通过学生动手操作，体验“能被3整除”的数与每个数字所在的位置无关，只是跟组成的数字和有关，这就给学生指明了一个探究的方向，顺利得出“能被3整除”的数的特征。但是，纵观整个教学过程，学生的探究还是被教师牵引着，教师没能再现学生自主探究的过程，而是给学生指明了获得知識的捷径，学生只是机械地执行了教师的一个指令，他们根本不知道为什么要用小圆片去摆数，糊里糊涂地做了一回“操作工”。这样的动手操作缺少了应有的探究味，降低了思维的含金量，充其量只是为了得出某个数学结论而附加的一个摆设，因此，课堂教学常常落入教师精心预设的轨道。

很显然，以上两次教学强调知识教学的“外显”、“灌输”、“注入”，将学生的大脑视为被动的知识容器，而忽视传授掌握知识的方法，忽视培养获取知识和运用知识的能力。这样的教学是一种复制式的或记忆式的活动。从短期看，知识掌握的效率比较高，但从长远看，学生不会自我拓展，大脑中的知识取决于教师灌输的信息和学生记忆储存的程度，久而久之，便降低了学生学习的效率。

三

[教学片段]

[学程＼&导航＼&1.第一次猜想。

生：我认为3的倍数的个位上的数是3、6、9，因为2和5的倍数都是看个位的。

2.否定第一次猜想。

生：我还有补充，我认为3的倍数的个位上的数还可以是1，比如21就是3的倍数。

学生分别举出了个位上数字不是3、6、9的3的倍数：15、84、57……

3.制定新的研究方案。

生：我们以前在学习2和5的倍数的时候，先找出一些2和5的倍数，再找出它们的规律，我想研究3的倍数也应该采用这样的方法。

4.第二次猜想与验证。

学生小组合作，纷纷举出一些3的倍数。

如：30、21、12、33、24、15、36、27、18、9。

学生在观察中，直觉发现3的倍数是个位上数字和十位上数字的和是3、6、9的数。

学生纷纷举例验证，如57、78、99等，发现两个数位上的数字之和是3的倍数，这个数就是3的倍数。

学生纷纷举出三位数、四位数、五位数是3的倍数的例子来验证这个猜想。

学生又列举出几个数的数字和不是3的倍数的数进行验证。

如：100、110……

结果发现：各个数位上的数字之和不是3的倍数，这个数就不是3的倍数，从中发现3的倍数的特征。

＼&师：我们学习了2和5的倍数的特征，那么3的倍数有什么特征呢？你能进行一个大胆地猜想吗？

师：刚才，大家根据2和5的倍数的特征，大胆地猜想3的倍数的特征是不是也是看个位？

师：从大家的举例中，我们马上就推翻了这个猜想。看来要否定一个猜想，只要举出一个反例就可以了。那么，我们该怎样去研究3的倍数呢？

师：这是我们研究数学的一个好方法，通过举例子去发现规律。大家可以先找一些3的倍数，然后再去发现3的倍数的特征。

师：一个两位数十位上的数字和个位上的数字的和是3、6、9，这个数就是3的倍数，那么，数字和是12、15、18的数是不是3的倍数呢？＼&]

[教学反思]这个教学设计遵循的是“学程导航”理论，是基于学生经验的建构。教师先让学生由2和5的倍数，类比推理产生3的倍数特征的猜想；再通过举例推翻这个猜想，从而产生研究问题的方法——举例子；通過观察学生举出的例子，得出又一个新的猜想，学生在教师点拨下，通过正反例子的验证，得出结论；最后从数形结合的角度，验证这个结论，从而确信这个结论的正确性。整个教学过程中，学生积累了丰富的“数理——逻辑经验”，在这个基础上认识数学知识的本质内涵，完成了数学知识的意义建构。学生从“知识仓库”中解放了出来，由一个知识的容器变为一个能动的认知体和生命体。教师从“机械传递知识的搬运工”中解放出来，由一个供学生利用的“资料库”变为一名“向导”和一名“顾问”。

在这节课中，我作了几点有益的探索：1. 培养学生类比推理的能力。学生由2和5的倍数的特征类比推理出3的倍数特征；由3的倍数的两位数的特征联想到3的倍数的三位数和四位数等特征。虽然类比推理使得出的结论不一定正确，还有待于验证，但它往往点燃了学生发现新知的火花。2.培养学生演绎推理的能力。对3的倍数为什么跟各个数位上数字的和有关，进行说理，虽然学生很难说清其中的道理，但是通过直观演示，还是发现了3的倍数的特征，而且将类比推理和演绎推理结合在一起，使学生受到了数学思想方法的熏陶。3. 经历探究的过程。在知识获得的过程中，感受了“观察——猜想——推翻猜想——再通过举例观察——再猜想——验证”的科学探究方法。4.学习探究的策略。举例验证，以退为进，以小见大，从位数少的两位数开始到多位数等等，这些都是留给学生终生有用的学习方式。5.感受科学的证明方法。要证明一个结论是否正确，需要大量的举例验证，而要否定一个错误的结论，只要举出一个反例就可以了。

总而言之，教学方式根植于教学观念，外显于教学行为，取决于教学设计，来源于数学教材。教师的教学观念应随着课程改革的深入而变。课程改革，观念为先，因此，“互动课堂，学程导航” 教学理念的实施与推广，不应仅仅停留在教材文本的处理上，更应体现在教师的教学行为、教学观念上。

（作者单位：江苏省海门市实验小学）