Bers型空间上加权复合微分前置算子
2017-05-30余建
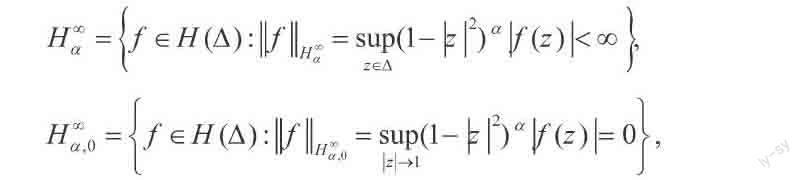
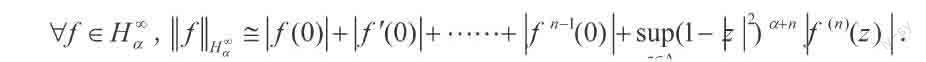
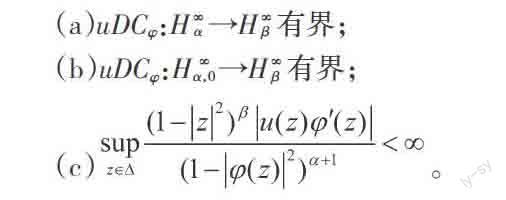
摘 要:从算子的性质出发,研究Bers型空间上的复合微分前置算子的有界性和紧性,得到了算子有界性和紧性的充分必要条件。
关键词:Bers型空间;复合微分前置算子;有界性;紧性
记Δ为复平面上的单位开圆盘,H(Δ)为Δ上解析函数的全体,对u,φ∈H(Δ)且u(Δ)?Δ,文献[1]给出了u,φ为符号的复合微分前置算子的定义:uDCφ f=uφ′f ′(φ),其中f∈H(Δ),Δ上的Bers型空间和小Bers空间分别定义为:
其中0<α<∞,显然,H
α是Banach空间,H∞
α,0是H∞
α的闭子空间。
国内很多学者研究了复合算子、微分算子以及复合微分算子在各类空间上的性质,取得了一系列成果。
文献[1]讨论了Qk(p,q)到α-Bloch 的加权复合微分前置的有界性和紧性,在Bers空间上的加权复合算子、加权复合微分算子也有比较多的研究(参看文献[3][4][5])。
本文主要研究Bers空间上的加权复合微分前置算子的性质。
本文还将用到函数I m(z)=zm,A?B是指存在常数C,使得?B?CB。文中每次出现C并不同一。
主要结果及其证明
在这个部分,将给出主要结果和证明以及证明所要用到的引理。
引理1[ 2 ] 设n?1为正整数,0<α<∞,则:
引理2[ 7 ] 假设φ是Δ上的解析自映射,则T:X→Y紧的充要条件是T:X→Y是有界,对所有X的有界序列(fk)在Δ的紧子集上一致收敛于0,则||Tfk||Y=0。
引理2的證明相仿文献[7]的定理3.11的证明,故此处省去。
定理1 设u∈H(Δ),u(Δ)?Δ,0<α,β<∞,φ是Δ上的解析自映射,则以下结论等价:
定理2 设u∈H(Δ),u(Δ)?Δ,0<α,β<∞,φ是Δ上的解析自映射。则以下结论等价:
另一方面,
参考文献:
[1] 龙见仁.Qk(p,q)空间到加权α-Bloch空间的复合微分后置和复合微分前置算子(英文)[J].贵州师范大学学报:自然科学版,2011(02):64-71.
[2] Zhu K.BLOCH TYPE SPACES OF ANALYTIC-FUNCTIONS[J].Rocky Mountain Journal of Mathematics,1993,23(3):1143-1177.
[3] 吴莹颖,张若静,唐笑敏.Bers型空间之间的加权微分复合算子[J].江西师范大学学报(自然科学版),2011,(06):610-613.
[4] 王茂发,刘云.不同Bers型空间之间的加权复合算子[J].数学物理学报,2007,(04):665-671.
[5] Zhu X.Generalized weighted composition operators from Bloch spaces into Bers-type spaces[J].Filomat,2012,26(6):1163-1169.
[6] 钟巧红.不同Bers-型空间之间的加权复合算子[J].广州大学学报(自然科学版),2006,(03):15-17.
[7] C.C.Cowen and B.D.MacCluer,Composition Operators on Spaces of Analytic Functions, Studies in Advanced Mathematics, CRC Press, Boca Raton,1995.
作者简介:余建(1990-),男,汉族,贵州瓮安人,贵州师范大学研究生,研究方向:函数论。
