高速永磁电机碳纤维护套转子综合特性研究
2017-05-30陈进华崔志琴
刘 威,陈进华,崔志琴,张 驰
(1.中北大学,太原 030051;2.中国科学院宁波材料技术与工程研究所,宁波 315201)
0 引 言
高速永磁电机由于体积小、转速高,可与工作机或负载直接相连,而被广泛应用于轻工业、制造业、航空航天等领域。高速永磁电机转子作为电机的传动装置,其设计和动力学分析已经成为国内外学者研究的热点[1]。
为了避免转子在起动过程和工作时产生共振,需要对电机转子的临界转速和振型进行相关的预测。转子上的磁性材料一般为稀土永磁材料,而其抗拉极限十分有限。当转子高速旋转时会产生巨大的离心力,必须对转子永磁体进行保护和强度校核。目前保护永磁体的主要措施是采用高强度的复合材料护套(如碳纤维)和高强度的非导磁金属护套(如钛合金)。与采用金属护套相比,高强度的复合材料具有质量轻、涡流损耗小的优点,因此碳纤维护套广泛应用于高速永磁电机永磁体的保护。但是碳纤维护套的散热能力差,极易导致永磁体局部高温最终永久性退磁。因此对电机进行整体的温升仿真计算是十分必要的。
HongDK等[2-3]通过有限元计算对120000 r/min高速电机转子进行了模态分析,并考虑了陀螺效应和不同刚度对临界转速的影响。随后,基于设计好的电机在考虑高速高温的情况下对多种工况下的护套进行强度分析。孙岩桦等[4]对滚动轴承和电磁轴承的转子进行了临界转速仿真,并通过实验法验证了仿真的正确性。黄梓嫄[5]对接触刚度因子进行优化,增加了磁悬浮转子的模态精度,并通过相关实验进行了证实。程文杰等[6]利用有限元法对多层过盈配合转子护套进行了转子应力的理论推导并进行了相关的验证。Wen S B等[7]对各向异性的复合材料转子进行了应力的理论推导,并作了相关的有限元仿真进行验证。张涛等[8]对高速永磁电机转子在高温高速时的情况下进行了转子应力推导和仿真计算,并提出了减少碳纤维应力的措施。王保俊等[9]对分块永磁体的转子强度进行了解析推导,并与有限元法的计算结果进行了比较。Kolondzovski Z等[10]对3种不同结构的转子护套通过有限元方法进行了分析和比较,结果表明钛合金材料相对性能较好。丁树业[11-12]对双馈风力发电机提出多种冷却方法,进行了相关的流体力学仿真。Dong J N[13]采用流固耦合的方法对油冷的高速永磁电机进行温度场分析。张凤阁[14]基于电磁场、转子强度、转子动力学、流体场和温度场等多物理场对一台兆瓦级、18 000 r/min的高速永磁电机进行了综合的分析,并进行了实验验证。
国内外学者对高速电机转子的研究往往从单一学科考虑,缺少从多方面去综合研究高速电机转子的方法。本文分别从临界转速、转子强度、温度场3个方面对一台20 kW,20 000 r/min的高速永磁电机转子进行综合分析。
1 高速永磁电机转子模型
本文研究的2极,20 kW,20 000 r/min高速永磁电机转子如图1所示。表贴式电机转子结构简单,主要由转轴、永磁体、护套3部分组成,其基本尺寸和参数如表1所示。

图1 表贴式电机转子模型
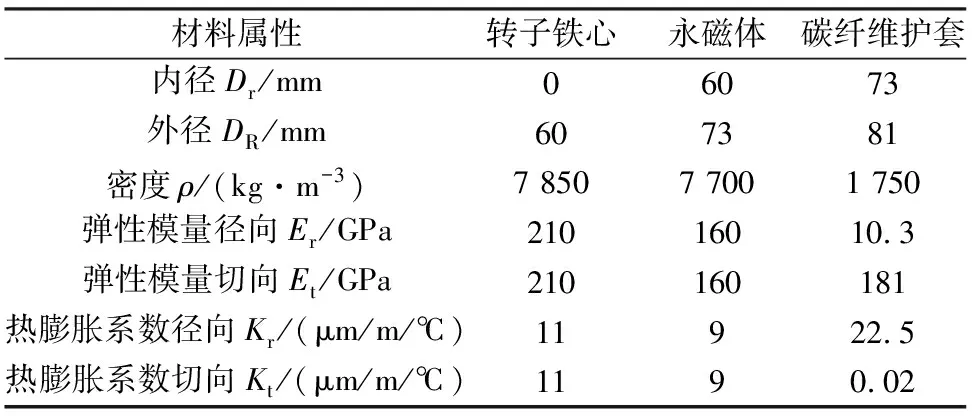
材料属性转子铁心永磁体碳纤维护套内径Dr/mm06073外径DR/mm607381密度ρ/(kg·m-3)7 8507 7001 750弹性模量径向Er/GPa21016010.3弹性模量切向Et/GPa210160181热膨胀系数径向Kr/(μm/m/℃)11922.5热膨胀系数切向Kt/(μm/m/℃)1190.02
2 转子动力学分析
2.1 模态分析理论
根据弹性力学理论,高速永磁电机转子动力学微分方程可以用下式表示:
kx(t)=Fx
(1)
ky(t)=Fy
(2)
式中:Ω是电机转子的角速度;m是电机转子的质量;k是转子轴承的刚度;Cn是电机转子系统的外部阻尼;Cr为电机转子系统的内部阻尼;x(t),y(t)分别为X,Y方向的位移向量;Fx,Fy分别为x,y方向的结构激振力。
电机转子位移同时可以用下式表示:
r(t)=x(t)+jy(t)=r0est
(3)
式中:r0为常数。
电机转子在自由转动时,Fx=Fy=0,将式(3)代入式(2)和式(1),可以推出:
ms2+(Cr+Cn)s+k-jΩCr=0
(4)
求解得:
(5)
从式(5)可以得出,S存在两个解,其中S的虚部代表自由转动时的固有频率。在考虑自由模态时,一般可以忽略阻尼,得到无阻尼的模态频率:
(6)
式中:ω1为转子正进动时的固有频率;ω2为转子反进动时的固有频率。
2.2 电机转子模态分析
对20 kW高速永磁电机转子进行模态分析,自由状态下的前2阶模态分析云图如图2所示,自由模态的第1阶振型和第2阶振型均为弯曲变形。在考虑轴承刚度的转子前2阶模态分析云图如图3所示,其前2阶振型也均为弯曲变形。两种状态下具体的固有频率和临界转速数值如表2所示。自由模态下的固有频率均大于同阶的轴承状态下的固有频率。电机转子自由模态第一阶临界转速为39 411 r/min,轴承状态下电机转子第1阶临界转速为23 311 r/min,均大于电机的额定转速20 000 r/min。

(a) 1阶模态

(b) 2阶模态
图2自由模态云图

(a) 1阶模态

(b) 2阶模态
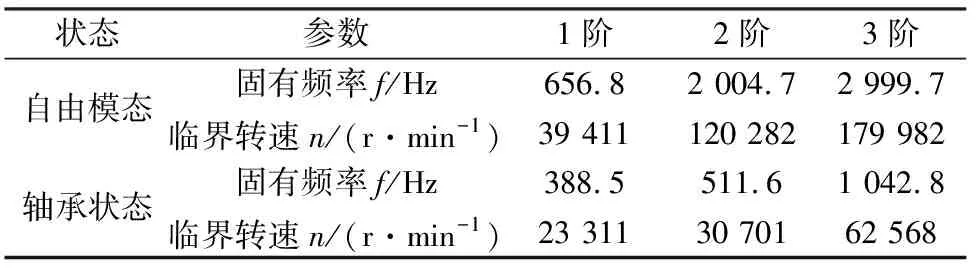
状态参数1阶2阶3阶自由模态固有频率f/Hz656.82 004.72 999.7临界转速n/(r·min-1)39 411120 282179 982轴承状态固有频率f/Hz388.5511.61 042.8临界转速n/(r·min-1)23 31130 70162 568
2.3 考虑实际工作情况的模态分析
从电机转子自由模态分析看出,电机转子在最右端的振幅最大。而电机转子的实际工作情况是连接负载进行高速旋转,在连接处(转子最右端)安装了轴承支撑。对电机转子最右端添加轴承约束进行模态分析,图4为在最右端添加轴承支撑约束之后的第1阶模态分析云图,第1阶振型为弯曲振动。

图4 实际工作情况下第一阶模态云图
转子右端加上轴承约束后抑制了右端的振动,第一阶振动区域变为中间部位。其固有频率和临界转速具体数值如表3所示。每一阶临界转速均大于轴承状态未考虑实际工作情况时的同阶临界转速。第1阶临界转速为29 877 r/min,相比未考虑实际工作情况时第1阶临界转速增大了28.2%,工作状态下的临界转速远大于额定转速,所设计的转子在考虑实际工作情况时符合设计要求。

表3 实际工作情况下电机转子模态分析结果
2.4 考虑陀螺效应电机转子模态分析
高速电机转子在高速旋转时具有像陀螺一样的现象,不会因为外力的加入而发生巨大的变化,会缓慢地绕着某一个轴发生小角度进动,陀螺效应会让电机转子继续保持旋转的惯性。因此在分析高速永磁电机转子动力学特性时必须考虑其陀螺效应。如图5所示,基于陀螺效应,可以画出电机转子相应的Campbell图。

图5 电机转子Campbell图
图5中Ratio=1的线段与各阶固有频率的红色三角形交点即为考虑陀螺效应下不同转速下的临界转速。在考虑陀螺效应后,电机转子模态分为正向进动与反向进动两个部分。
随着转速的增大,正向进动的频率随之增大,反向进动的频率随之下降。如表4所示,随着转速的增加,正向进动和反向进动的变化幅度很小,几乎可以忽略。

表4 高速永磁电机转子模态分析结果
2.5 刚度对临界转速的影响
电机转子两端安装轴承固定转子,轴承类型和轴承刚度的合理选择对电机的正常运转影响巨大,因此选取合适的轴承刚度,避免共振对电机转子设计有重要的意义。图6为不同轴承刚度下电机转子前4阶临界转速变化曲线。随着轴承刚度的增加,各阶临界转速逐渐增大。第1阶临界转速是转子设计最为关心的部分,随着刚度的增加,第1阶临界转速的增幅逐渐变缓,趋于一条直线,可见刚度对临界转速的影响在低刚度下效果显著,在高刚度下没有较大的影响。

图6 轴承刚度对弯曲模态临界转速的影响
2.6 转子系统起动瞬态分析
对电机转子进行瞬态分析,在5 s内将电机转子转速从0逐渐升至30 000 r/min,取电机转子系统的最大不平衡响应,如图7所示。随着转速的增大,最大变形量随之增大,在30 000 r/min时,转子最大变形量为0.15 μm,符合设计要求。

图7 转子系统的最大不平衡响应
3 转子强度研究
目前,转子护套一般采用碳纤维护套。由于永磁体在高速旋转下会产生巨大的离心力,而永磁体一般采用烧结钕铁硼材料,其抗拉极限仅为80 MPa,在装配过程中永磁体和碳纤维护套过盈配合,会使永磁体产生一定的预紧力,从而减小正常运转时的拉应力。
如图8所示,在高速温升下的情况下,永磁体最大切向力为17.2 MPa,出现在永磁体内表面,最小切向力出现在永磁体外表面为3.8 MPa,均为正值,为拉应力。切向力从外表面逐渐增大至内表面,在允许的80 MPa的范围内。同样情况下的永磁体径向力如图9所示,最大值出现在内表面,58.4 MPa,为压应力,最小值出现在外表面53.0 MPa,同样为负值,为压应力,永磁体径向抗压极限为1 050 MPa,仿真结果在允许范围内。

图8 永磁体切向力
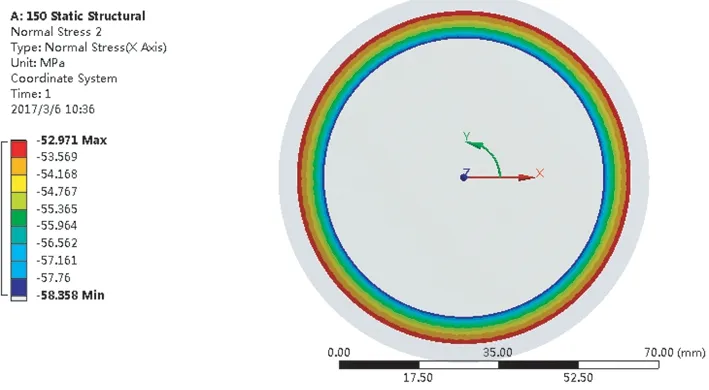
图9 永磁体径向应力
4 转子温度场研究
由于转子护套为碳纤维材料,其散热能力差,极易导致永磁体高温,使永磁体产生不可逆退磁。如图10所示,对已设计好的1/18电机模型进行温度场仿真。应用CFD流体力学软件,设置其计算边界条件:
1) 外壳采用直槽水道,内风道采用强迫风冷。直槽水道入口速度为3 m/s,内风道入口速度为15 m/s,入口温度均设置为20℃。
2) 电机护套和转轴部分由于和内风道相接处,其接触面设置转速为20 000 r/min,模拟转子旋转。
3) 电机模型由于是1/18电机模型,电机两侧采用旋转周期对称边界条件。
4) 电机整体的前后两端采用绝热面。
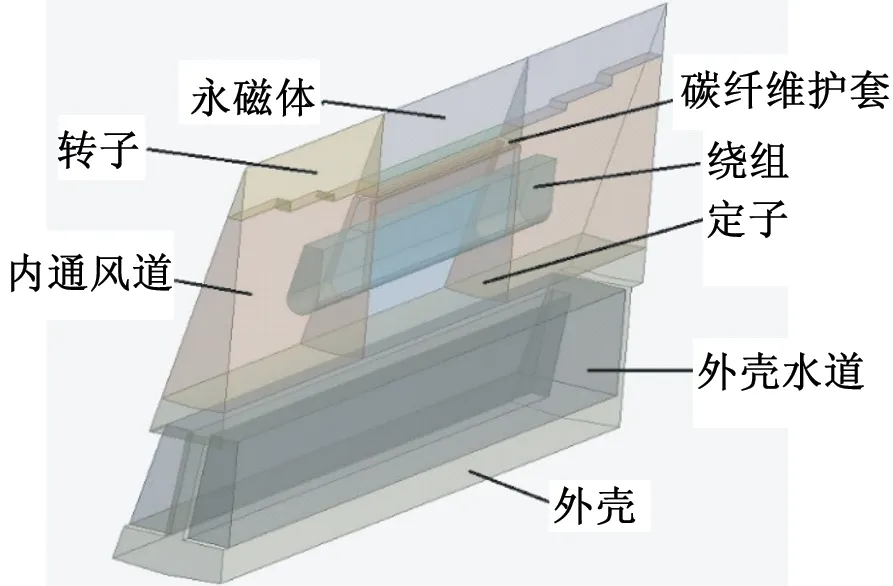
图10 CFD电机模型
仿真结果如图11所示,电机的最高温度为108.3 ℃,出现在转轴永磁体部位,这是由于碳纤维护套散热性差所导致,碳纤维护套的传热系数仅为0.7 w/(m·k),其他材料的传热能力远大于为碳纤维。钕铁硼永磁体的工作温度一般在150 ℃以下,仿真结果显示在允许范围内。
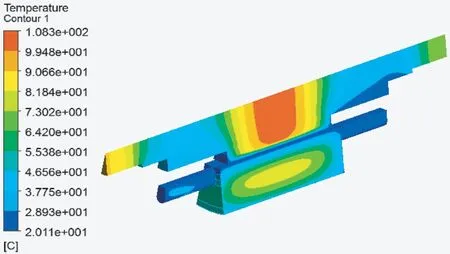
图11 电机温升图
5 结 语
本文对一台20 kW,20 000 r/min高速永磁电机进行了电机转子的临界转速、转子强度、温度场地分析,提出了一套基于多学科考虑的电机转子结构分析方法,得出以下结论:
1) 分别从自由模态、轴承支撑状态、考虑实际工作3种情况对电机转子临界转速进行了分析,并研究了陀螺效应和轴承刚度对临界转速的影响,并做了瞬态分析研究。
2) 钕铁硼永磁体抗拉极限有限,对碳纤维护套的电机转子进行了应力分析,表明应力满足设计要求。
3) 对电机进行了整体温升仿真,发现最大温度出现在转子中部靠近永磁体部位,这是碳纤维护套散热性差所导致的,温升结果在允许范围内。
[1] 闫阿儒,张驰.新型稀土永磁材料与永磁电机[M].北京:科学出版社,2014.
[2] HONG D K,WOO B C,JEONG Y H,et al.Development of an ultra high speed permanent magnet synchronous motor[J].Internationl Journal of precision engineering and manufacturing,2013,14(3):493-499.
[3] HONG D K,JOO D,WOO B C,et al.Performance verification of a high speed motor-generator for a microturbine generator[J].Internationl Journal of precision engineering and manufacturing,2013,14(7):1237-1244.
[4] 田野,孙岩桦,丁成伟,等.不同支撑和转子装配方式的高速电机临界转速分析[J].振动与冲击,2013,32(8):24-30.
[5] 黄梓嫄,韩邦成,周银锋.非线性接触下磁悬浮电机柔性转子系统模态分析[J].中国电机工程学报,2014,34(15):2438-2444.
[6] 程文杰,耿海鹏,冯圣,等.高速永磁同步电机转子强度分析[J].中国电机工程学报,2012,32(27):87-94.
[7] WEN S B,JIANG S Y.Optimum design of hybrid composite multi-ring flywheel rotor based on displacement method[J].Composites Science and Technology,2012(72):982-988.
[8] 张涛,朱熀秋,孙晓东,等.基于有限元法的高速永磁转子强度分析[J].电机与控制学报,2012,16(6):63-68.
[9] 王保俊,毕刘新,陈亮亮,等.碳纤维绑扎表贴式高速永磁电机转子强度分析[J].浙江大学学报:工学版,2014,47(12):2101-2110.
[10] KOLONDZOVSKi Z,SALLINEN P,BELAHCEN A,et al.Rotordynamic analysis of different rotor structures for high-speed per-
manent magnet electrical machines[J].IET Electric Power Applications,2010,4(7):516-524.
[11] 丁树业,葛云中,徐殿国,等.1.5MW 双馈风力发电机内流体场分析[J].中国电机工程学报,2012,32(21):93-97.
[12] 丁树业,孙兆琼,徐殿国,等.3MW 双馈风力发电机传热特性数值研究[J].中国电机工程学报,2012,32(3):137-143.
[13] DONG J N,HUANG Y K,JIN L,et al.Thermal optimization of a high-speed permanent magnet motor[J].IEEE Transactions on Magnetics,2014,50(2):749-752.
[14] 张凤阁, 杜光辉, 王天煜, 等. 1.12 MW高速永磁电机多物理场综合设计[J] .电工技术学报,2015,30(12):171-180.
