基于滑模控制的SRM直接瞬时转矩控制研究

於天浩，吴国庆,2，茅靖峰，谭 阳

(1.南通大学,南通 226019 2.江苏省风能应用技术工程中心，南通 226019)

0 引 言

开关磁阻电机(以下简称SRM)结构简单、变速运行范围宽、低速运行性能好、可靠性高、运行效率高，与其他电动机相比有自身优势，未来有望成为主流调速电动机[1]。但由于SRM的定子凸极结构和非线性电磁特性，其转矩波动较大限制了发展[2-3]。

本文引入直接瞬时转矩控制(以下简称DITC)方法，在SRM DITC转速外环引入动态滑模控制，以提高系统的动、静性能[7]，如图1所示。传统抑制转矩波动的方法一般都是通过控制点电流、电压和角度间接控制转矩，因此很难精确控制转矩。DITC方法直接控制任意时刻的瞬时转矩，避免了优化电流等变量时需要的复杂算法[4-6]；同时鉴于SRM具有四象限运行的特点，常规PID难以获得理想的性能。

图1 基于DITC的SRM系统框图

1 滑模控制速度调节器设计

1.1 滑模控制原理

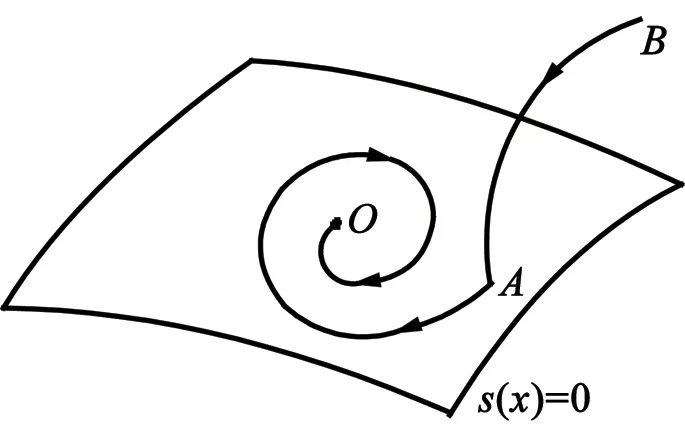
图2 滑模变结构动态图

图2为滑模控制的基本原理图。假设系统滑模变量x是给定值与反馈值之间的偏差量。图2中原点O是滑模变量的终点。滑模面s取：

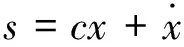
(1)

滑模控制量定义：

(2)

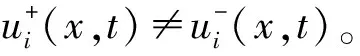
图2中的AO段为滑模控制下状态变量的轨迹。BA段是趋近运动，系统状态变量从B点运行到滑模面的A点。控制律ui+(x,t)或ui-(x,t)，系统结构能够保持。

由滑模控制理论可知，对于任何一个无扰动非线性系统，有：

(3)

式中:x为状态量；u为输入量。

取滑模面：

s=cx

(4)

式中:c为滑模面参数，满足赫尔维茨多项式。那么把式(3)代入式(4)得：

(5)

ueq1=-(cb)-1cf(x)

(6)

而对于一个不确定非线性系统，往往满足如下方程:

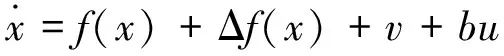
(7)

式中:Δf(x)为系统自身变量；v为系统外部扰动。现将内外干扰综合考虑得d=Δf(x)+v，则式(7)可写为：

(8)

同理得到系统式(8)的等效控制:

ueq=-(cb)-1cf(x)-(cb)-1cd

(9)

(10)

为了加速系统收敛速率，本文采取指数收敛率：

(11)

这里，ε是任一大于0的常数；α是指数系数，且0<α<1。ε|s|α具有负反馈的特点，其绝对值大小决定了滑模函数运动过程中收敛速率。然后，选取雅普诺夫函数V=s2/2，可以得到：

(12)

因此，证明式(9)中的控制量能保证运动在滑模面上，并且能在有限的时间内收敛[8-10]。

1.2 滑模控制器设计

(13)

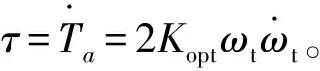
s(t,x)=cx1+x2

(14)

将式(14)两边同时求导得：

(15)

根据式(15)选择指数收敛率，可以计算推出控制量Tref的表达式：

(16)

2 DITC设计

2.1 不对称桥式功率变换器的相开关状态

本文采用不对称桥式功率变化电路，由相开关管VT1D,VT1U和续流二极管VD1D,VD1U组成，图3给出了一相绕组上的开关状态。

(a) S=1 (b) S=0 (c) S=-1

图3中，S表示开关状态。各相之间独立控制，简单可靠。同时，根据功率变换器工作过程，可以把开关动作分为3个状态：

(17)

2.2 转矩计算单元

在SRM的DITC中，瞬时转矩的计算非常重要，瞬时转矩估算公式：

(18)

式中：Tj为第j相瞬时转矩；θ为转子位置角；ij为第j相电流；W′(θ,ij)为磁共能。

由式(18)可知，W′(θ,ij)由θ和ij共同决定，当电磁路饱和时，磁化曲线呈严重非线性，很难实时解析磁共能，所以在忽略磁饱和的情况下，式(18)可简化：

(19)

以一相转矩特性为例，如图4所示,已知一相电流和角度则可得相瞬时转矩，其余6相依此计算，最终六相相加即为发电机瞬时转矩Ttotal。将Ttotal和Tref偏差值送入DITC单元，输出理想开关信号，系统转矩波动得以抑制。

图4 转矩特性仿真模型

2.3 DITC单元

在SRM运行时，相电感根据角度位置的不同，可分为单相导通和换相导通区域，示意图如图5所示。

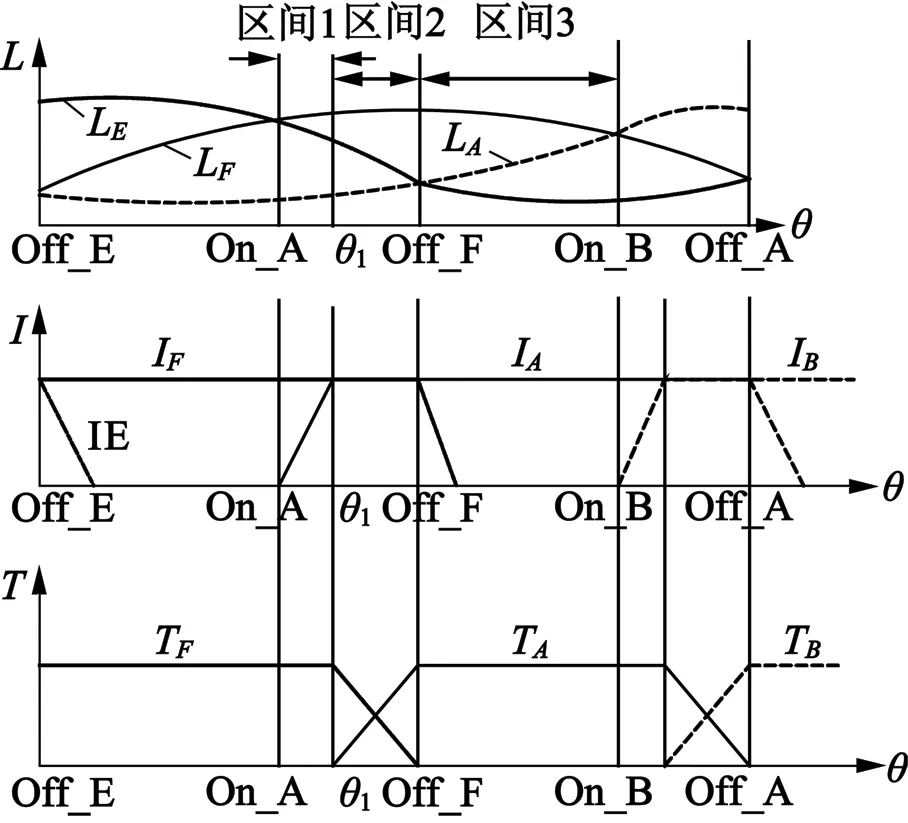
图5 转矩分配示意图

在不同的SRM运行模式下，需要采用不同的开关状态。电动模式下，不采用负电压，而在制动模式下，则需要采用负电压。图6为DITC电动运行转矩滞环示意图，令ΔT=|Tref|-|Tcst|，ΔT表示转矩偏差，相应的开关状态依据以下原则确定。

(a) 单相运行

(b) 两相即将关断切换

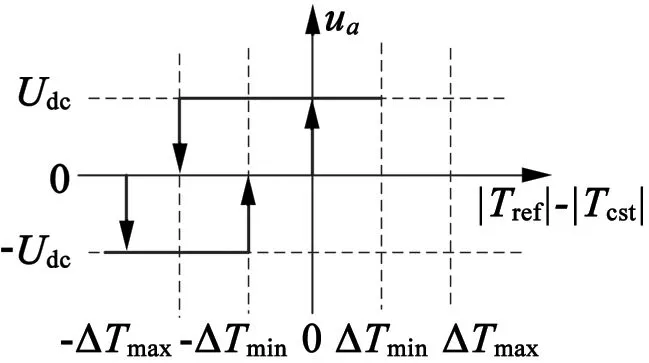
(c) 两相即将运行切换

在单相导通区域，开关状态如表1所示，转矩偏差进入DITC单元，控制单相导通区域Ttotal跟随Tref。

表1 单相区开关状态表

两相邻相同时运行的区域称为换相区，在换相区域，即将运行相具有增加转矩的优先权，所以其转矩滞环阈值小于即将关断相的阈值。表2显示了换

表2 换相区开关状态表

相区开关状态,假设初期两相(A,B)开关状态都是S=1。这样，通过DITC的开关调节，换相区的瞬时转矩也实现了控制。

3 仿真实验及分析

在MATLAB/Simulink环境下搭建了基于DITC的SRM控制系统，如图7所示。其参数设置： 开关磁阻发电机：六相(12/10)，额定功率Pn=3 kW，额定电压Un=110 V，额定转速nN=500 r/min，相绕组电阻R=0.14 Ω，最大电感Lmax=30 mH，最小电感Lmin=4 mH，转动惯量J=0.008 1 kg/m2，摩擦系数μ=0.000 1；空气密度ρ=1.205 kg/m3。

在常规PI控制中，选定参数为Kp=8，Ki=5;采样时间Ts=1×10-6s。图8是ω=50 rad/s时常规PI控制器的转速和转矩，图9则是ω=50 rad/s时SMC控制器的转速和转矩。

图7 滑模控制SRM DITC系统仿真模型

图8 DITC系统下，ω=50 rad/s常规PI输出转速和转矩

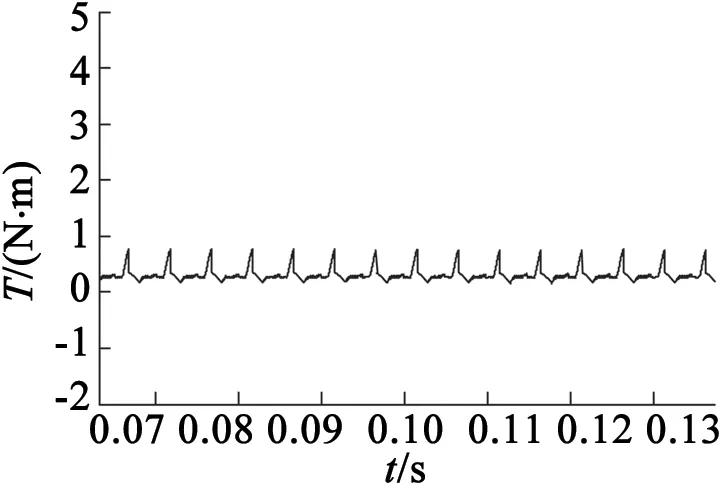
图9 DITC系统下，ω=50 rad/s SMC输出转速和转矩

由图8、图9可以看出，常规PI控制器参数固定，无法在较宽的调速范围内保持优良的控制性能。而常规PI的SRM DITC系统，给定角速度50 rad/s时转速略有波动，但转矩波动较大。SMC是一种智能控制算法，适应性强。从图10可以看出，转速调节器采用SMC的SRM DITC系统给定角速度50 rad/s时，转速波动小、超调小，同时转矩脉动仍然较小。

当ω=40 rad/s时，在电机运行稳定时加上一个负载扰动，图10为SMC控制器加了扰动后输出转速与转矩变化情况。可以看出，其转速在加入负载扰动瞬间，变化平缓，而且电机能够再次稳定运行转速恢复到40 rad/s，说明SMC的抗负载扰动能力强。

图10 ω=40 rad/s加入干扰SMC输出转速和转矩

4 结 语

本文在SRM转矩控制中采用DITC控制方法，同时在转速外环引入滑模控制器取代常规PI控制器，仿真表明，和常规PI比较，速度调节器采用滑模控制器的SRM DITC系统在较高速度时具有较好的动、静态性能及抗负载能力。

[1] 王宏华.开关磁阻电动机调速控制技术[M].北京：机械工业出版社，2014.

[2] NARLA S，SOZER Y，HUSAIN I．Switched reluctance generator controls for optimal power generation and battery charging[J].IEEE Transactions on Industry Applications,2012,48(5):1452-1459.

[3] ZHOU Suying，LIN Hui．Modeling and simuimion of switched reluctance motor double closed loop control system[C]//proeeding of the 6th World Congresson Intelligent Control and Automation,June 21.Dalian,2006:6151-6155.

[4] 吴红星.开关磁阻电机系统理论与控制技术[M].北京:中国电力出版社，2010.

[5] Robert B. Inderka，Rik W. De Doncker．Direct instantaneous torque control of switched reluctance drives[C]//IEEE 37th IAS Annual meeting,USA,2002:1605-1609.

[6] LIN Zhengyu,REAY D S,BARRY W.Ripple Reduction in switched reluctance motor drives using B-spline neural networks[J].IEEE Industry Applications Society,200,42(6):1445-1453.

[7] 茅靖峰,吴爱华,吴国庆,等.基于扩张状态观测的永磁直驱风力发电系统MPPT自适应滑模控制[J].电力系统保护与控制，2014,42(18):58-64.

[8] 李墨翰,李玉忍.基于滑模变结构的开关磁阻电机控制仿真[J].计算机仿真,2009,26(12):351-354.

[9] LI Yan,TANG Yi,CHANG Jibin et al.Continuous sliding mode control and simulation of SRM[C]//IEEE International conference on Cognitive Informatics & Cognitive Computing,2011:314-317.

[10] 邓君,詹琼华,孙剑波.开关磁阻电机滑模变结构速度控制[J].微电机,2006,39(7):1-4.