一类奇摄动双曲型非线性积分-微分系统

冯依虎,莫嘉琪

(1.亳州学院电子与信息工程系，安徽亳州236800; 2.安徽师范大学数学系,安徽芜湖241003)

一类奇摄动双曲型非线性积分-微分系统

冯依虎1,莫嘉琪2

(1.亳州学院电子与信息工程系，安徽亳州236800; 2.安徽师范大学数学系,安徽芜湖241003)

本文研究了一类两参数双曲型非线性积分-微分奇摄动系统.首先利用Fredholm型积分方程,得到了系统的外部解;然后用多重尺度变量方法得到了系统的边界层校正项,再利用伸长变量方法得到了系统的初始层校正项;最后由不动点理论证明了奇摄动解的合成渐近展开式的一致有效性.

积分-微分方程;奇摄动;双曲型方程

0 引言

非线性双曲型积分-微分系统在应用数学、工程数学、连续介质力学、量子力学、建筑学、物理化学等学科中有许多应用.奇摄动理论和方法,已被广泛地应用在数学物理、弹性力学、流体力学和生物化学等自然科学中,许多学者已经做了研究[1-10].作者等在这方面也做了一些工作[11-17].本文是利用奇摄动理论来讨论一类双曲型积分-微分系统的模型.

考虑如下一类双曲型积分-微分系统模型

其中ε、µ是小的正参数,

x≡(x1,x2,···,xn)∈Ω,Ω是Rn中的有界区域,∂Ω为Ω的C1+α类的边界(α∈(0,1)为H¨older指数),L为一致椭圆型算子,T0为正常数,T为积分算子,ψ(x)和K(x,y)＞0为连续函数.

系统模型(1)—(4)是具有两参数的积分-微分方程初始边值问题.我们来研究它的奇摄动解.首先作如下假设.

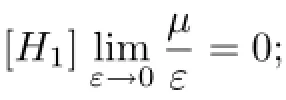
[H2]aij,ψ,fi,gi和hji(i=1,2,···,m,j=1,2)关于它们的变元在对应的区域内为光滑的函数,且gi(0,x)=h1i(x),x∈∂Ω,i=1,2,···,m;

[H3]fi(t,x,ui,0,0)=0,fiui(t,x,ui,ε,µ)≤-c1＜0,其中c1为正常数.

1 Fredholm型积分方程

模型(1)—(4)的退化系统为

再假设

[H4]非线性积分方程(5)有解Ui00(x),i=0,1,···,m.

构造模型(1)—(4)的外部解U=(U1,Un,···,Un).设

将(6)式代入双曲型积分-微分方程(1),按ε和µ的幂展开非线性扰动函数项fi,合并εrµs同次幂的系数并分别令其为零.关于ε0µ0的系数为零,就是积分方程(5).它的解为Ui00(x)(i=0,1,···,m).关于εrµs(r,s=0,1,···,r+s/=0)的系数为零,得Fredholm型积分方程

其中

由积分方程(7),可以得到解.再由(5)、(7)式得到的解Uirs(r,s=0,1,···,i=1,2,···,m)代入(6)式,便得到了模型(1)—(4)的外部解U=(U1,U2,···,Um).但它未必满足边界条件(2)和初始条件(3)、(4).因此我们尚需构造边界层校正项V=(V1,V2,···,Vm)和初始层校正项W=(W1,W2,···,Wm).

2 多重尺度变量与边界层校正

首先在区域Ω的边界∂Ω的邻域上建立局部坐标系(ρ,φ)∶规定在区域Ω的边界∂Ω的邻域内的每一点P的坐标ρ(≤ρ0)为点P到∂Ω的距离,其中ρ0为足够小的正常数,使得在边界∂Ω上的每一点的内法线在∂Ω的邻域0≤ρ≤ρ0内相互不相交.而坐标φ=(φ1,φ2,···,φn-1)是在n-1维流形∂Ω上的一个非奇坐标系,并设点P的坐标φ就是通过点P的内法线和边界∂Ω的交点Q的坐标φ.故在∂Ω的邻域0≤ρ≤ρ0中的算子L为

在∂Ω的邻域0≤ρ≤ρ0上引入多重尺度变量[1-2]

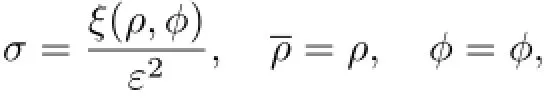
其中ξ(ρ,φ)为待定函数,它将在下文中决定.为了方便,以下我们仍以ρ来表示这时由(8)式有

其中

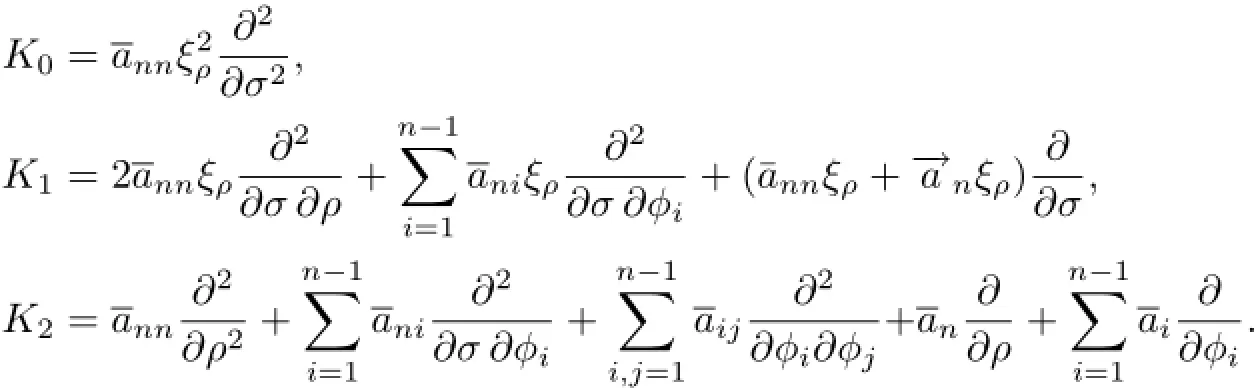
设双曲型积分-微分系统(1)—(4)的解为u=(u1,u2,···,um),其中

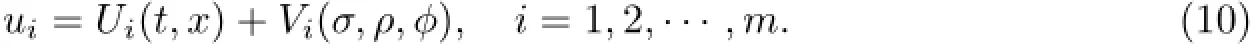
将(10)式代入(1)、(2)式,得到

将(10)、(13)式代入(11)、(12)式,按ε和µ的幂展开非线性函数的项,合并εrµs的同次幂项的系数,有

其中Girs为逐次已知的函数,它们的结构从略.

由积分-微分系统(14)—(17)式,可依次得到virs(r,s=1,2,···,i=1,2,···,m).并由假设知virs具有如下边界层性态

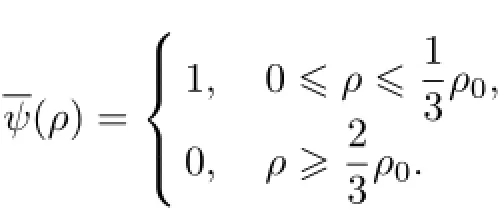
为了方便,以下仍然以virs将得到的virs(i=1,2,···,m)代入(13)式,我们便得到了双曲型积分-微分系统初始边值问题(1)—(4)的边界层校正函数V= (V1,V2,···,Vm).

3 伸长变量与初始层校正

设

和

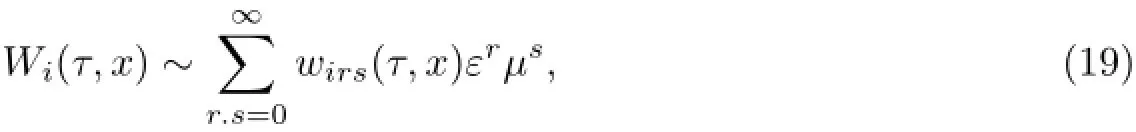
将(18)、(19)式代入(1)、(3)、(4)式,按ε,µ展开非线性项,再由εrµs同次幂的系数,得到

由此我们便能构造两参数非线性双曲型积分-微分系统初始边值问题(1)—(4)的解(u1,u2,···,um)有如下形式的渐近展开式

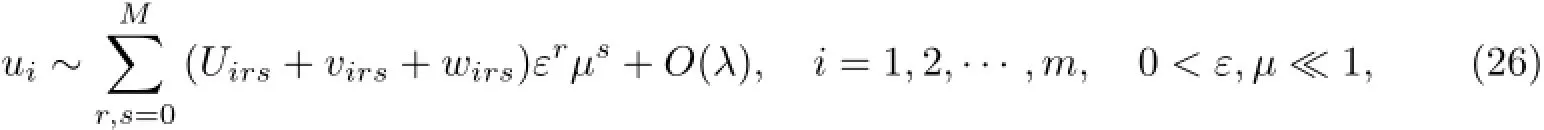
其中λ=max(εM+1µM,εMµM+1).

4 举例

考虑如下一类波动方程积分-微分初始边值问题

其中t,x分别为时间、空间变量,u(t,x)为波的振动位移函数,ε,µ是小的正参数,扰动项函数f(u,ε,µ)=(ε+µ)exp(-u),而积分算子Tu为

问题(27)—(30)是具有两参数的波动积分-微分方程初始边值问题.我们利用本文的方法来求得其奇摄动渐近解.

显然,Fredholm型积分方程(32)的解为U00(t,x)=0.

再由(7)式,U01,U10分别满足

由U00(t,x)=0和(31)式,可分别得到积分方程(33)、(34)的解为

于是波动方程积分-微分初始边值问题(27)—(30)的外部解U的展开式为

其次,在x=0的邻域设利用多重尺度方法,由(14)—(17)式可依次得到

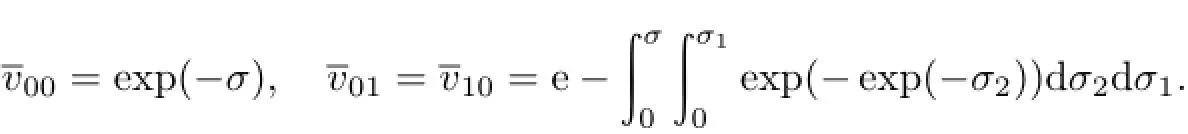
于是,在x=0的邻域的边界层校正项的渐近表示式

同样,在x=1的邻域设

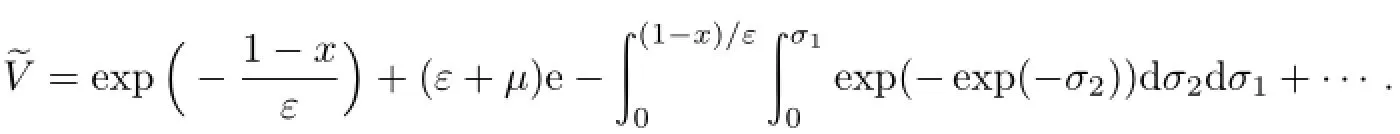
由此,便得到波动方程积分-微分初始边值问题(27)—(30)在区域[0,1]的“边界”(端点)x= 0,x=1邻域的合成边界层校正项V为

其中S0为x=0的邻域,S1为x=1的邻域.

再在t=0的邻域设利用伸长变量变换法,由问题(21)—(23)和(24)—(26)可得

于是波动方程积分-微分初始边值问题(27)—(30)的初始层校正项W的渐近展开式为

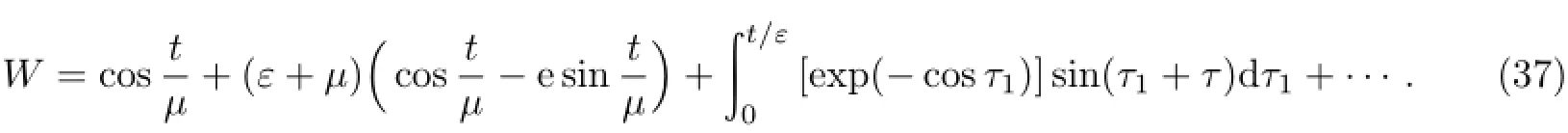
最后由(35)—(36)式,便得到波动方程积分-微分初始边值问题(27)—(30)波的振动位移函数u(t,x)的形式渐近展开式

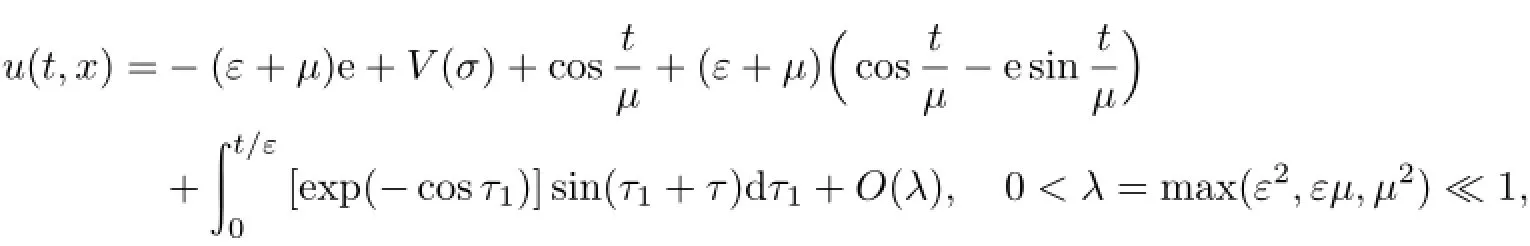
其中边界层校正项V(σ)由(37)式表示.

5 不动点原理和解的一致有效性

现证明渐近式(26)为双曲型积分-微分系统(1)—(4)解的一致有效的渐近展开式.

首先,设N是个线性赋范空间,B是Banach空间.设F为由N到B的非线性映射,且F[0]=0.并设F[p]可分解为F[p]=L[p]+Ψ[p],其中L为在p=0时F的线性化算子.算子L和Ψ满足如下条件∶

(I)L-1为L的连续逆映射,且

其中l为不依赖于q的正常数.

(II)KN(r)表示球{p|p∈N,‖p‖≤r},存在正数满足Lipschitz条件∶‖Ψ[p2]-Ψ[p1]‖≤m(r)‖p2-p1‖,∀p1,p2∈KN(r),0≤r≤并且当r→0时m(r)单调下降为零.现有如下泛函分析不动点定理.

定理1[1-2]在上述条件(I)、(II)下,设r0=sup{r|0≤r的任何f∈B,存在p∈N,使得F[p]=f,且||p||≤2l-1||f||≤r0.

现用上述不动点原理来估计双曲型积分-微分系统(1)—(4)渐近解(26)的余项R.设

利用(38)式和性态(18)、(26)式,有

固定ε,µ,选择线性赋范空间N为

由不动点假设,成立

其中l是不依赖于ε,µ的正数,的连续逆算子.Lipschitz条件为

其中C1,C2和C为独立于ε,µ的常数,并对任意的p1,p2,在球KN(r)(‖r‖≤1)中成立.再由定理1,奇摄动非线性双曲型积分-微分系统(1)—(4)的解的渐近展开式(38)的余项R满足

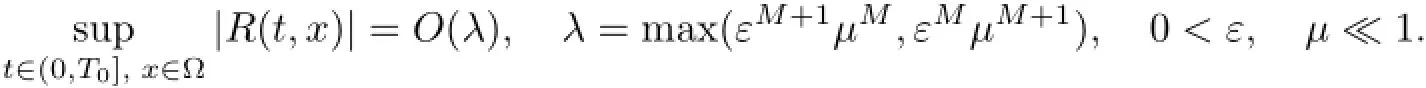
于是有如下定理.

定理2在假设[H1]—[H4]下,奇摄动非线性双曲型积分-微分系统(1)—(4)存在一个解上关于ε,µ成立一致有效的渐近展开式(38).

[1]DE JAGER E M,JIANG F R.The Theory of Singular Perturbation[M].Amsterdam:North-Holland Publishing Co,1996.

[2]BARBU L,MOROSANU G.Singularly Perturbed Boundary-Value Problems[M].Basel:Birkhauser,2007.

[3]CHANG K W,HOWES F A.Nonlinear Singular Perturbation Phenomena:Theory and Applications[M].Applied Mathematical Science,56,New York:Springer-Verlag,1984.

[4]SAMUSENKO P F.Asymptotic integration of degenerate singularly perturbed systems of parabolic partial differential equations[J].J Math Sci,2013,189(5):834-847.

[5]MARTINEZ S,WOLANSKI N.A singular perturbation problem for a quasi-linear operator satisfying the natural condition of Lieberman[J].SIAM J Math Anal,2009,41(1):318-359.

[6]KELLOGG R B,KOPTEVA N A.Singularly perturbed semilinear reaction-dif f usion problem in a polygonal domain[J].J Dif f er Equations,2010,248(1):184-208.

[7]TIAN C R,ZHU P.Existence and asymptotic behavior of solutions for quasilinear parabolic systems[J].Acta Appl Math,2012,121(1):157-173.

[8]SKRYNNIKOV Y.Solving initial value problem by matching asymptotic expansions[J].SIAM J Appl Math, 2012,72(1):405-416.

[9]KELLY W G.A singular perturbation problem of Carrier and Pearson[J].J Math Anal Appl,2001,255:678-697.

[10]MIZOGUCHI N,YANAGIDA E.Life span of solutions for a semilinear parabolic problem with small dif f usion [J].J Math Anal Appl,2001,261:350-368.

[11]MO J Q.Singular perturbation for a boundary value problem of fourth order nonlinear differential equation[J]. Chin Ann Math B,1987(1):80-88.

[12]MO J Q.Singular perturbation for a class of nonlinear reaction dif f usion systems[J].Science in China,1989,32: 1306-1315.

[13]MO J Q.A singularly perturbed nonlinear boundary value problem[J].J Math Ana1 Appl,1993,178:289-293.

[14]MO J Q.Homotopic mapping solving method for gain f l uency of a laser pulse amplif i er[J].Science in China G, 2009,52(7):1007-1010.

[15]FENG Y H,LIU S D.Spike layer solutions of some quadratic singular perturbation problems with high-order turning points[J].Math Appl,2014,27(1):50-55.

[16]冯依虎,石兰芳,汪维刚,等.一类广义非线性强阻尼扰动发展方程的行波解[J].应用数学和力学,2015,36(3):315-324.

[17]冯依虎,石兰芳,汪维刚,等.一类大气尘埃等离子体扩散模型研究[J].应用数学和力学,2015,36(6):639-650.

(责任编辑：林磊)

A class of singularly perturbed hyperbolic nonlinear integral-differential system

FENG Yi-hu1,MO Jia-qi2
(1.Department of Electronics and Information Engineering,Bozhou College, Bozhou Anhui236800,China; 2.Department of Mathematics,Anhui Normal University,Wuhu Anhui241003,China)

A class of singularly perturbed system for the hyperbolic nonlinear integraldifferential system is considered.Firstly,the outer solution to system is obtained by employing the Fredholm type integral equation.Then the boundary layer corrective term is constructed using the variables of multiple scales method.And the initial layer corrective term is found via the stretched variable method.Finally,from the f i xed point theory,the uniformly valid behavior for the composed asymptotic expansion of singular perturbation solution is proved.

integral-differential equation;singular perturbation;hyperbolic type equation

O175.29

A

10.3969/j.issn.1000-5641.2017.03.004

1000-5641(2017)03-0039-09

2016-03-17

国家自然科学基金(11202106);安徽省教育厅自然科学重点基金(KJ2015A347,KJ2017A702);安徽省高校优秀青年人才支持计划重点项目(gxyqZD2016520);亳州学院科学研究项目(BSKY201431)

冯依虎,男,硕士,副教授,研究方向为应用数学.E-mail：fengyihubzsz@163.com.