未知杂波状态下基于箱粒子滤波的PHD算法

魏 帅，冯新喜，王 泉

(空军工程大学信息与导航学院，陕西 西安710077)

未知杂波状态下基于箱粒子滤波的PHD算法

魏 帅，冯新喜，王 泉

(空军工程大学信息与导航学院，陕西 西安710077)

针对未知杂波环境中，传统的多目标概率假设密度(PHD)滤波器跟踪精度无法保证，所需粒子支撑集过大导致效率低下的问题，引入了区间分析技术，提出了未知杂波状态下基于箱粒子滤波的PHD算法。该算法首先完成对雷达目标和杂波的混合空间随机有限集模型的构建，然后基于箱粒子滤波技术，利用量测数据建立未知杂波模型，推导出目标状态更新方程，并用多目标箱粒子PHD滤波递推地估计目标状态。仿真实验表明，当杂波环境与先验模型不匹配时，相较于多目标粒子滤波算法，该算法在保证目标跟踪性能的同时，有效减少了算法的计算时间。

多目标跟踪；概率假设密度；区间分析；箱粒子；未知杂波

0 引言

传统的多目标跟踪算法多需要对数据进行关联[1-2]，工作量较大，实时性较低。基于此，Mahler提出随机有限集统计学(Random Finite Set, RFS)的多目标跟踪算法，解决了目标数未知且可变的问题。为便于实现，Mahler继而提出概率假设密度(Probability Hypothesis Density, PHD)滤波算法[3]，将复杂的多目标状态空间的运算转换为单目标状态空间的运算，降低了计算复杂度，保证了目标跟踪的精度，因而有很高的理论意义与研究价值[4]。

传统的PHD滤波将杂波建立为已知的泊松分布过程，用κk(z)完全概括表示，表示k时刻杂波有限集Kk的强度[5]。但实际中，因存在复杂环境、人为电子以及目标不可见性的干扰等影响，导致目标信号较弱甚至消失在杂波或干扰信号中，从而增加了杂波虚警，使得目标信噪比下降，同时，对于杂波的估计与分析又会增加耗时。文献[6]假设杂波具有时变的非结构参数,在执行每一步时均要估计时变参数。文献[7-8]分别利用瑞利分布和κ分布对杂波进行建模，而这些算法仅仅只是假设杂波参数未知，其模型结构仍然已知，且无法直接应用于随机集滤波中。文献[9]提出利用有限混合模型来描述杂波的密度函数,利用马尔科夫链蒙特卡罗算法[10]估计该混合模型参数，但仅适用于杂波数远大于目标数的情况，并通常假设杂波数已知。文献[11]利用目标和杂波联合状态空间模型估计杂波模型,但假设空间分布概率密度函数已知，只完成对杂波数的估计。文献[12]着眼于泊松点过程理论，假设多目标跟踪模型服从泊松点过程，并进行泊松过程强度的贝叶斯递归，得到概率密度函数递推公式，但因仿真实验设置参数较为复杂，实现结果并不理想。文献[13-14]提出了一种未知杂波环境下的PHD滤波器，通过量测对杂波模型进行估计，并用序贯蒙特卡罗(Sequential Monte Carlo, SMC)方法实现，因杂波的先验知识未知，对杂波的估计致使运算量较大，耗时较多。

分析可知，未知杂波环境中，传统的多目标PHD滤波器跟踪精度无法保证，所需粒子支撑集过大导致效率低下。本文针对此问题，引入了区间分析技术，提出了未知杂波状态下基于箱粒子滤波的PHD算法。

1 未知杂波环境下跟踪问题描述

未知杂波环境的跟踪问题主要考虑的是该环境下的随机集滤波问题。基于混合空间模型，分别给出雷达目标和杂波的强度表达式。

1.1 空间模型建立

考虑建立混合空间模型进行算法实现。定义如下：

χ=x⊕λ

其中，χ表示混合空间，x为目标状态空间，λ为杂波空间，且两者在统计意义上独立，⊕表示两个集合的并集。

实质上，PHD滤波器是已知杂波与新生目标强度的滤波器，通过传播后验强度函数完成对目标数的估计[14]，从而估计出各个目标的状态。但实际中，并不能保证目标的量测值与状态估计完全对应。因此在基于未知杂波的环境下，考虑将PHD的相关计算从原本标准的目标状态空间拓展到混合空间中，反映雷达目标和杂波两部分信息。

1.2 未知杂波环境下的PHD滤波

在所建立的混合空间模型中，对未知杂波环境下的PHD滤波进行算法递推运算。算法可分为两大部分，预测部分和更新部分，每一部分均需要考虑目标和杂波两种递推过程。

在预测部分中，假设给定k-1时刻的后验强度vk-1，则k时刻目标和杂波所预测的强度分别为：

(1)

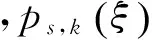
在更新部分中，假定给定k时刻的目标预测强度vk|k-1和量测集Zk，则目标和杂波的更新强度分别为：

(2)

其中，

(3)

显然，该模型是基于未知杂波环境中，利用量测数据建立杂波模型，覆盖状态空间的粒子数目越多，越能精确地拟合目标量测值，获得更准确的目标状态估计。因此考虑寻找一种高效的实现算法来代替原有的粒子滤波算法。

2 未知杂波环境下基于区间分析的PHD滤波算法实现

传统的SMC-PHD[15]和文献[13]中的SMC-NPHD是在未知杂波环境采用粒子滤波算法，用带权值的样本点来近似逼近后验概率密度从而进行实现。而过大的粒子支撑集势必会引起计算量的大幅增加，因此导致算法运行时间较长。针对该问题，本文提出将箱粒子滤波算法引入未知杂波的环境中，形成基于区间分析的PHD滤波算法(Box-SMC-NPHD)，以此来代替原本的粒子滤波算法，从而提高在未知杂波环境下的PHD算法运行效率。

1)初始化

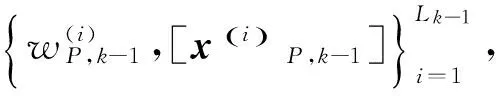
(4)

一般假设衍生目标通常出现在量测位置，因此可根据先前时刻的量测衍生出当前时刻的新生目标状态粒子，并用一组均匀分布的概率密度函数和表示，如式(5)所示：

(5)

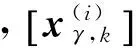
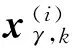
(6)

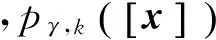
(7)

其中，总体箱粒子数目表达式为：

Lk=Lk-1+Lγ,k

2)预测目标PHD

设k-1时刻的后验强度为vk-1，即

(8)

预测强度的总表达式如下：

(9)

(10)

(11)

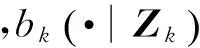
3)预测杂波强度

(12)

4)更新目标

设k时刻的预测强度vk|k-1，即

(13)

更新后的强度为：

(14)

(15)

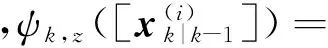
5)更新杂波强度

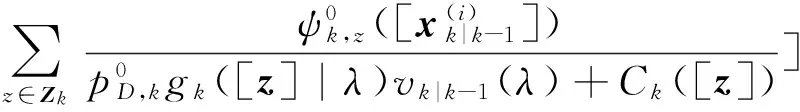
(16)

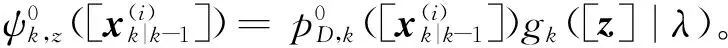
6)约束箱粒子

(17)

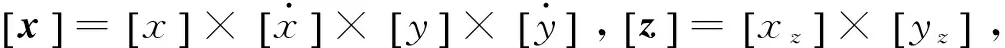
7)估计目标数目

期望的目标数目表达式为：

8)重采样

假定Lk为重采样的粒子数，根据箱粒子在重采样过程中的复制次数，划分箱粒子，并对权值进行归一化运算，重采样后的箱粒子集为：

9)目标状态提取

将箱粒子最终转化为点粒子，依据所估目标数目将重采样后的粒子用K-means算法进行聚类，由聚类中心得到目标状态。选取权值大于某一门限的粒子，从而得到目标状态估计的表达式，即：

3 仿真实验与算法结果分析

为验证算法的效性和可行性，将SMC-PHD，SMC-NPHD和Box-SMC-NPHD算法进行比较。

3.1 实验参数设定

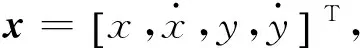
xk=Fxk-1+Γwk

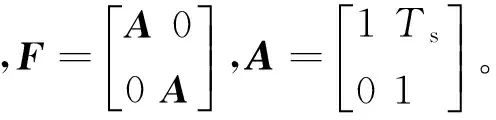
目标1持续时间为1～8 s；目标2持续时间为7～20 s；目标3持续时间为12～35 s；目标4持续时间为28～40 s。

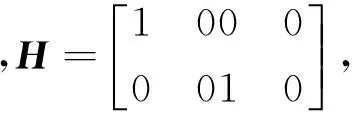
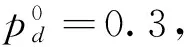
3.2 实验结果与分析

基于多目标跟踪的框架下，在考虑估计目标数目的同时，也需要估计目标的各自状态，因此选用最优子模式分配(OSPA)距离作为评价准则指标，OSPA包括位置和集合势两部分距离，其中距离敏感性参数p表征距离误差，水平调节数c表征集合势误差，考虑距离误差比势误差更为重要[16]，选取参数c=50，p=2。对每个区间量测，取滤波持续粒子数为2 000，新生粒子数50，箱粒子滤波的持续粒子数为40，新生粒子数为1。分别对不同算法在100次蒙特卡洛实验条件下进行仿真比较，并分析运行时间结果。区间分析工具采用Intlab工具箱。

图1给出了四个目标在杂波环境下的运动轨迹。考虑基于未知杂波环境的仿真环境，分别取较低、中等和较高杂波密度进行比较实验，对应取值分别为3×10-5，1.5×10-4，3×10-4，并假设杂波密度在实行跟踪的时间区间内基本保持不变。

图2表示SMC-PHD，SMC-NPHD与Box-SMC-NPHD滤波算法在三种不同杂波环境下的目标数估计与OSPA距离。由图2(b)可以看出，在中等杂波密度下，三种算法均可较好估计目标数目，这是因为中等杂波密度与传统PHD滤波先验杂波模型较为匹配。由图2(a)，(c)可以看出，在较低或较高的杂波密度下，即杂波密度与先验模型不匹配的情况下，Box-SMC-NPHD较SMC-PHD与SMC-NPHD可以更精准地估计目标数目。

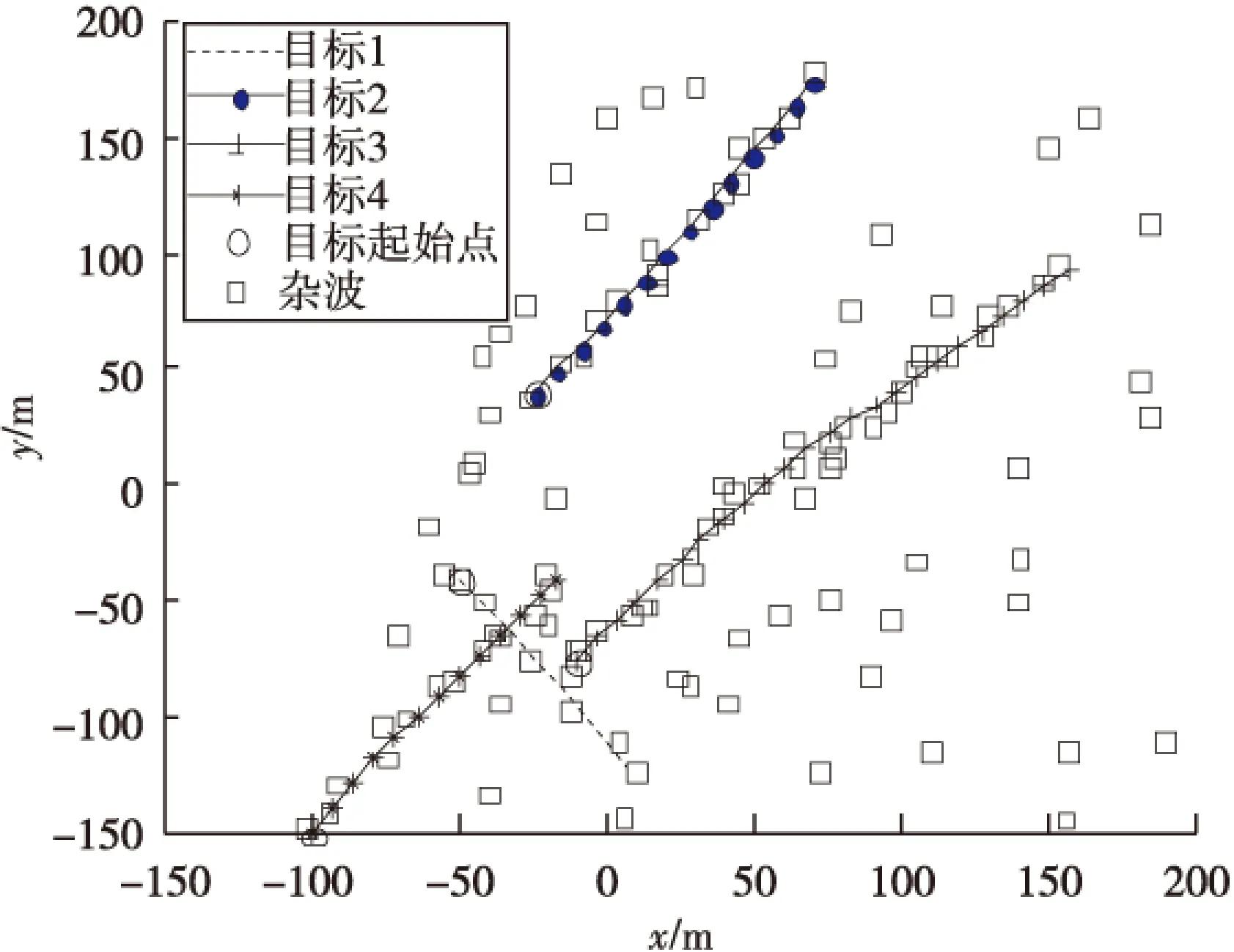
图1 目标运动轨迹和带杂波的区间量测Fig.1 Target trajectory and interval measurement with clutters

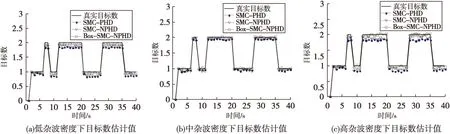
图2 三种滤波算法在不同杂波环境下目标数估计Fig.2 Three filter simulation comparison on target number estimation in different clutter situations

比较分析图3(a)，(b)，(c)可知，在三种杂波密度下，基于粒子滤波的SMC-NPHD和基于箱粒子滤波的Box-SMC-NPHD的OSPA值均小于SMC-PHD，即前两者比传统PHD粒子滤波算法更能稳健地跟踪目标状态。在低、中密度杂波情况下，前两者的OSPA均值基本相当，但是在高密度杂波下，前者则比后者低5.81%。这是因为高密度的杂波环境是一种更加明显的不精确测量环境，该环境下对杂波估计的要求更高，而基于区间分析的滤波方法利用区间量测变量代替点变量进行运算，降低了计算的复杂性，使得测量更加精准，在进行杂波估计的过程中表现出更好的鲁棒性。实验结果表明，所提算法可以更为有效地适应未知杂波密度尤其是高杂波密度跟踪环境，更准确地反映雷达目标运动状态。

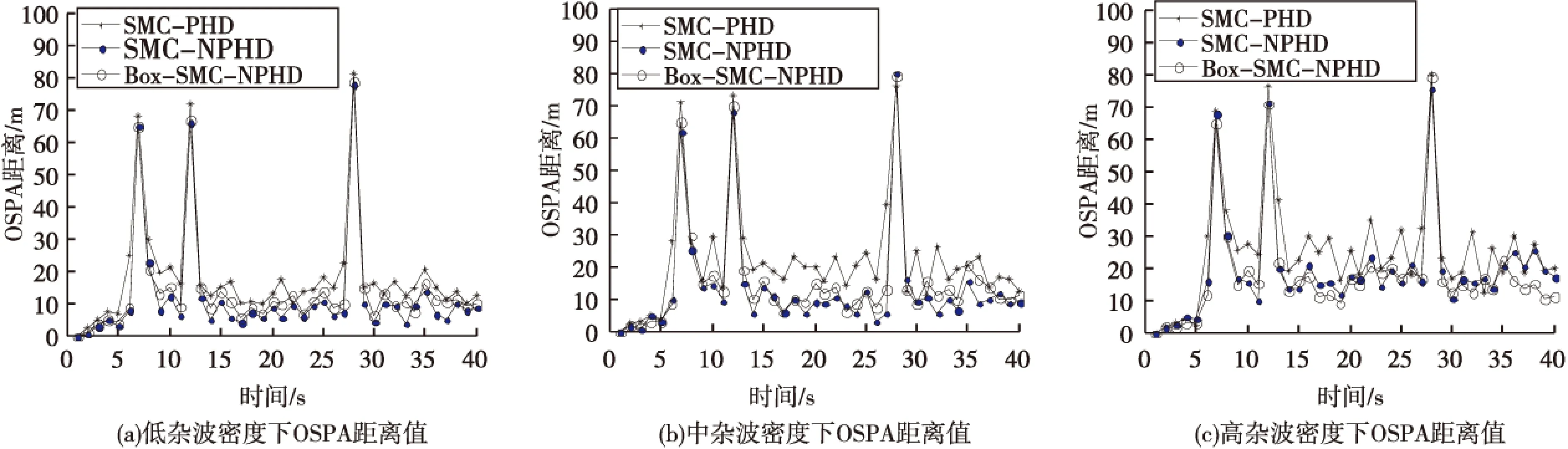
图3 三种滤波算法在不同杂波环境下OSPA值比较Fig.3 Three filter simulation comparison on OSPA distance in different clutter situations

表1给出三种滤波算法的运行时间，可看出SMC-NPHD比SMC-PHD多耗时约20%，而基于区间分析的Box-SMC-NPHD却是SMC-NPHD运行时间的1/6左右。这是因为本文的改进算法所需的箱粒子数要远远小于其余两种粒子滤波算法。后两者基于粒子滤波的算法需要2 050个粒子，由于用较多的新生粒子数来捕获新生目标，因而导致时间的大量消耗。前者基于箱粒子滤波的改进算法虽然在区间分析上会花费一部分时间，但只需要41个箱粒子就可达到与粒子滤波算法相似的精度，粒子数目的大量减少使得算法在整体上实现了运行时间的大幅度降低，从而提高了时效性和应用性。

表1 三种算法的运行时间比较

Tab.1 Three filters comparison on time running in different clutter situations

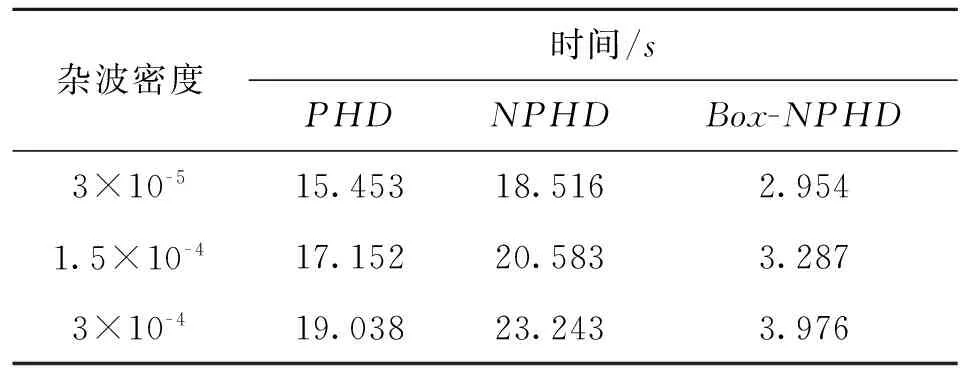
杂波密度时间/sPHDNPHDBox-NPHD3×10-515.45318.5162.9541.5×10-417.15220.5833.2873×10-419.03823.2433.976

4 结论

本文提出了未知杂波环境下基于箱粒子滤波的PHD算法。该算法采用箱式粒子加权的方法，利用量测数据建立未知杂波模型，推导出目标状态更新方程，并用多目标箱粒子PHD滤波递推地估计目标状态，大大降低了所需粒子数。仿真实验表明，当杂波环境与先验模型不匹配时，相较于多目标粒子滤波算法，该算法在保证目标跟踪性能的同时，有效减少了算法的计算时间。一方面保证了跟踪精度与鲁棒性，尤其在较低与较高杂波密度下表现出较好的性能；另一方面大幅度节省了运行时间，具有较高的时效性和工程应用性。但作为一种较新的滤波算法，箱粒子滤波发展时间较短，具体的理论细化还有待完善。如箱粒子滤波算法的收敛性问题仍需解决；重采样采用随机子划分重采样，方法较为单一，因此找到多样的采样方法有利于更好地适用于更多实际情况。

[1]Hue C, Cadre J L, Perez P.Sequential Monte Carlo methods for multiple target tracking and data fusion[J].IEEE Transactions on Signal Processing, 2002, 50(2): 309-325.

[2]李志鹏，赵捍东，李元.基于粒子群改进粒子滤波的机动目标跟踪方法[J].探测与控制学报，2014，36(3)：31-35.

[3]王晓，韩崇昭，连峰.基于随机有限集的目标跟踪方法研究及最新进展[J].工程数学学报，2012,29(4): 567-578.

[4]欧阳成.基于随机集理论的被动多传感器多目标跟踪[D].西安：西安电子科技大学, 2011．

[5]Mahler R.Statistical Multi-source multi-target Information Fusion[M].Boston: Artech House Publishers,2007.

[6]Vo B T, Vo B N, Cantoni A.Analytic implementations of the cardinalized probability hypothesis density filter[J].IEEE Transactions on Signal Processing.2007,55(7): 3553-3567.

[7]Musicki D, Morelande M, Scala B L.No parametric target tracking in non uniform clutter[C]// The 8th International Conference on Information Fusion.Philadelphia, USA，2005:1-6.

[8]GRuttenM,GordonNJ,MaskellS.Recursivetrack-before-detectwithtargetamplitudefluctuations[J].IEEEProceedings:Radar,SonarandNavigation，2005,152:345-352.

[9]LianFeng,HanChongzhao,LiuWeifeng.EstimatingUnknownClutterIntensityforPHDFilter[J].IEEETransactionsonAerospaceandElectronicSystems, 2010,46(4):2066-2078.

[10]WatanabeR,OkamuraH,DohiT.AnEfficientMCMCAlgorithmforContinuousPHDistributions[C]//ProceedingsoftheWinterSimulationConference.NewYork:IEEE,2012:1-12.

[11]MahlerR,VoBT，VoBN.CPHDFilteringwithUnknownClutterRateandDetectionProfile[J].IEEETransactionsonSignalProcessing，2011,59(8):3497-3513.

[12]StreitR.PoissonPointProcesses:Imaging,Tracking,andSensing[M].Heidelberg:Springer, 2010.

[13]SchikoraM,GningA,MihaylovaL,etal.Box-particleIntensityFilter[C]//9thIETDataFusionandTargetTrackingConference.Stevenage:IET, 2012: 1-6.

[14]李翠芸,江舟,姬红兵.一种新的未知杂波环境下的PHD滤波器[J].西安电子科技大学学报, 2014,41(5):18-23.

[15]VoBN,SinghS,DoucetA.SequentialMonteCarlomethodsformulti-targetfilteringwithrandomfinitesets[J].IEEETransactionsonAerospaceandElectronicSystems, 2005,41(4): 1224-1245.

[16]刘伟峰，文成林.随机集多目标跟踪性能评价指标比较与分析[J].光电工程, 2010, 37(9):14-26.

A PHD Algorithm Based on Box Particle in Unknown Clutter Environment

WEI Shuai， FENG Xinxi， WANG Quan

(Information and Navigation College of Air Force Engineering University, Xi’an 710077, China)

In unknown clutter environment, traditional Probability Hypothesis Density(PHD) filter in multi-target tracking cannot guarantee a good performance, and multitude number of particles leads to time consuming and low efficiency. Aiming at the problems, a new PHD filter tracking algorithm in unknown clutter environment based on interval analysis was proposed. Firstly, radar targets and clutter disjoint union state space modeled were established in random finite set. Next, Using measurement model to set up clutter model and derived to multi-target updated state function based on box particles. Additionally, the state of multi-target was recursively estimated in utilization of PHD filter box particles. Simulation revealed that the proposed algorithm was able to dramatically lower computational time with better tracking performance compared with traditional box particle filter.

multi-target tracking; probability hypothesis density; interval analysis; box particle; unknown clutter

2016-12-20 基金项目:国家自然科学基金项目资助(61571458)；陕西省自然科学基金项目资助(2011JM8023)

魏帅(1993—),女，北京人，硕士研究生，研究方向：多目标跟踪。E-mail: tear0419@qq.com。

TN953

A

1008-1194(2017)02-0094-06