基于节点撕裂和化学反应优化算法的接地网故障诊断

周 斌 ，彭敏放 ，黄清秀 ，荆 晶 ，沈美娥

（1.湖南大学 电气与信息工程学院，湖南 长沙 410082；2.北京信息科技大学 计算机学院，北京 100101）

0 引言

接地网对于电力系统的运行安全可靠性、工作人员和电气设备的安全起着至关重要的作用。我国发生过多次接地网事故，对它们的调查表明，接地网腐蚀严重影响地网的完整性和散流特性，是导致交流接地网损坏故障最突出的技术问题之一［1-3］。目前在工程上发现接地电阻不合格、地网故障引发事故或运行到一定年限时，往往通过大面积的开挖来检查，这种方法具有一定的盲目性，并且工作量大、速度缓慢，影响电力系统的正常运行。因此，在不停电和不对地网大面积开挖的情况下，实现对接地网的故障诊断具有重要的意义。

目前关于接地网腐蚀故障诊断的方法主要分为3类：采用电磁场的方法实现故障诊断，基于电化学的方法实现故障诊断和以电网络理论为基础并结合优化算法实现故障诊断。其中，文献［4］通过量测地面附近磁场分布的方法来判断接地网断裂部位，很好地探测出了导体的断裂情况。文献［5］利用电化学的方法，较好地检测出了直接与接地引下线相连的接地网导体故障，且实现较容易。文献［6］采用准稳态测量来得到表征接地导体腐蚀状态的极化电阻值，以诊断接地导体的腐蚀速率和腐蚀程度，在检测接地导体的局部腐蚀状态时获得了较好的结果。文献［7］利用电网络分析方法，建立了诊断方程，并采用优化算法求解，由于该方法建立起的故障诊断方程一般有多个解，研究人员进一步采用了遗传算法［8］、最小二乘法［9］、禁忌搜索算法［10］等优化算法对其唯一求解。上述方法都有一定的优势，但对初值的要求高，且容易陷入局部最优。

本文在已有的应用电网络理论和智能优化算法进行接地网故障诊断的方法的基础上，通过融合节点撕裂、虚拟分子理论和化学反应优化CRO（Chemical Reaction Optimization）算法建立接地网故障诊断数学模型，然后采用改进后的化学反应优化算法进行求解。通过仿真计算与分析，验证了本文方法的准确性和有效性。

1 接地网故障诊断模型的建立

1.1 基本原理

对于一个有n个节点、b条支路的接地网，忽略其每条支路的电感和电容，可以将其等效成一个纯电阻网络，且该网络为线性时不变网络［7］。将已知的接地网撕裂成Ns个子网络和1个自由支路集，且每个子网络都为连通图［11］。设有ks个撕裂的可及节点，未撕裂部分由us个可及节点和Vs个不可及节点组成。则该子网络的节点电压方程为：

其中，Yn为节点导纳矩阵；Un为节点电压列向量；In为节点注入电流列向量。原网络电流源的电流和等效注入电流共同组成撕裂节点的电流。

消去式（1）中未撕裂的不可及节点可得：

其中，Usv为撕裂不可及节点的电压向量；Usu、Is1分别为未撕裂可及节点的电压向量和电流向量；Usk、Is2、Isk分别为撕裂可及节点的电压向量、电流源向量和撕裂节点等效注入电流向量。

对式（2）应用初等行变换［12］消去其不可及节点电压向量 Usv，得到子网络的等效模型［13］为：

其中，系数矩阵]为子网络的等效不定节点导纳矩阵，其具体数值由子网络拓扑结构和支路电阻值决定。

整理式（3）可以得到：

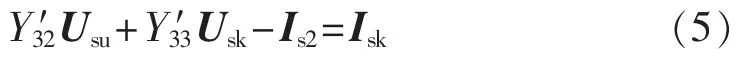
其中，式（4）描述了等效不定节点导纳与可及节点电压之间的非线性关系，而式（5）等式右端列向量相加之和为撕裂节点处广义节点的电流代数和。

1.2 模型建立

通过上述分析，根据广义节点电流相容性理论建立等效子网络［13］的多目标优化函数模型为：

其中，Iski为撕裂可及节点的等效注入电流；Rj为第j条支路的电阻参数；R为对应支路电阻的标称值；bm为子网络Sm所含的支路个数。

在实际应用中，多目标求解问题的最终目标是求解一个适合该实际应用的折衷解，为得到这个多目标最优的解，现有方法一般是先形成一个帕累托最优解集，然后在这个最优解集中选择需要的解。为了简化多目标的求解步骤，本文利用虚拟分子理论［14］来改进接地网多目标故障诊断模型，其中心思想是以距离理想解的远近来判断分子结构的优劣，其基本原理如图1所示。

图1 虚拟分子理论基本原理Fig.1 Basic principle of virtual molecular theory

图1中，点 P 的坐标为（F1min，F2min，F3min），（F1，F2，F3）为3个目标函数同时取得最优的点，点P是只考虑一个目标函数时取得的3个最优解组成的点，由于3个目标函数相互制约，一般不能够得到绝对理想的点。图1分为A、B、C、D 4个区域，事实上区域A是多目标问题中不可能优化到的区域，剩余区域是能够被优化到的区域。通过对比可以发现，图1的点1—5中点1最接近点P，利用虚拟分子理论可以得出点1为最优点。点P虽然是实际中不能达到的一个理想点，但它对算法中的分子结构起到指引的作用，即指引新的分子无限接近理想点P，从而达到优化的目的。利用此理论可将其数学模型改进为：

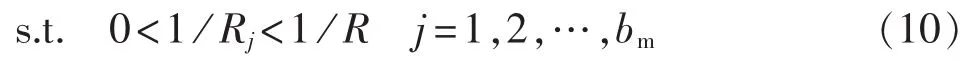
其中，（F1min，F2min，F3min）为目标函数的一个理想化的点，由于本文是由2个目标函数构成的多目标问题，故设定 F3、F3min为 0。

2 模型的求解

2.1 化学反应优化算法

化学反应优化算法是基于化学反应过程中分子碰撞和能量转化过程的群体智能算法［15-16］，具有群规模动态变化、个体之间信息交换方式丰富等特征［17］。

化学反应优化算法通过分子的结构来表征所求解的问题，其势能表示对应的目标函数值，最优解是尽可能地找到势能最低点。首先采用分子与容器壁之间及分子之间的无效碰撞构成的强度策略搜索其紧邻区域，当不能在邻域内继续找到更低的能量状态时，采用分子的分解和合成构成的多样化策略跳到一个相对较远的区域继续搜索，在搜索过程中，通过多种交换方式，能量会在分子间不断地重新分配。

算法初始值的选择对计算结果有较大的影响，为了使本文算法有较好的收敛速度、搜索精度和寻优能力，采用随机方式生成初始分子种群。相关参数主要包括：分子种群规模（PopSize），即初始阶段定义的分子个数；中央能量缓冲器（Buffer），它在分子反应过程中存储和补充分子能量，一般将其初始值设置为0；分子的初始动能（initialKE），它是改变分子结构的一个测量值，能使分子在转变过程中获得更有利的分子结构；分子动能损失率（KelossRate），它用来限制分子动能损失的百分比；分子反应类型的决定因子（MoleColl），它用来判定分子将发生哪种反应。

算法初始阶段参数设置的具体步骤如下：

a.在分子各属性的取值范围内采用随机的方式形成一个随机的分子；

b.判断随机产生的分子是否满足约束条件，若满足则进入步骤c，否则返回步骤a；

c.计算分子的势能，设定分子的初始动能，并将分子保存到反应容器中，同时校验容器中初始分子种群是否达到设定的初始规模，若达到则结束初始化过程，否则返回步骤a。

2.2 算法的改进

化学反应优化算法存在着收敛速度慢、易早熟等缺点。针对化学反应优化算法易陷入早熟的缺点，本文结合混沌策略无序、随机的特点，提出一种改进措施。

令Bu为可行域的上界，Bd为可行域的下界，xbest=（x1，x2，…，xn）为当前最优状态位置，则先按式（11）所示映射规则进行映射：

显然，映射后的区间为［0，1］，所以可以利用Logistic 映射产生混沌变量［18-19］如式（12）所示。

其中，μ为控制参数，取值μ=4时，系统处于完全混沌状态，有利于跳出局部最优。

最后，通过式（13）将混沌变量逆映射到所求的解域，重复此过程，直到函数值不再改变。

利用上述Logistic映射对化学反应优化算法进行改进，即当化学反应优化算法得到的解不变时，考虑采用混沌策略产生新的解，比较其与原解的适应度函数大小，并保留更优者。

改进化学反应优化算法流程如图2所示。

图2 改进化学反应优化算法流程Fig.2 Flowchart of improved CRO algorithm

2.3 基于改进化学反应优化算法的接地网诊断

基于改进化学反应优化算法的接地网故障诊断步骤为：

a.依据电网络基本理论，采用节点撕裂法的思想将待诊断的接地网拓扑图进行撕裂分块；

b.根据待诊断接地网拓扑结构，利用MATLAB/Simulink搭建出仿真电路模型；

c.采用轮换直流激励的方法，测试出每次测量的可及节点电压；

d.利用优化理论并结合虚拟分子理论建立接地网故障诊断数学模型；

e.在MATLAB中调用改进化学反应优化算法程序求解诊断模型；

f.计算诊断结果与支路标称值的倍数，判断接地网腐蚀故障的位置及腐蚀程度。

3 算例及其分析

某变电站接地网拓扑结构如图3所示，其共有66条支路、40个节点，节点40为参考节点，节点2、3、6、8、10、11、13、14、16、18、21、23、27、29、30、33、37 为可及节点。为了减少诊断方程的病态程度，根据接地网的拓扑结构，从节点13、21、29、37处将网络撕裂成2个子网络和3条自由支路集合，如图4所示。

接地网是埋在地下的，只能通过引下线进行激励和测量。而在引下线施加直流电流源激励时，由于接地网自身的原因，会对接地网的故障诊断产生一定的影响。因此，为了减小直流电流源激励对故障诊断的影响，本文采用轮换激励的方法，即通过改变激励的位置，测量出更多的数据。在节点激励电流源注入位置的选择上，本文选择在可及节点之间施加激励电流源，这样可以有效地提高接地网诊断的准确性，同时能够更好地诊断出发生故障的位置。

图3 接地网拓扑结构图Fig.3 Topology of grounding grid

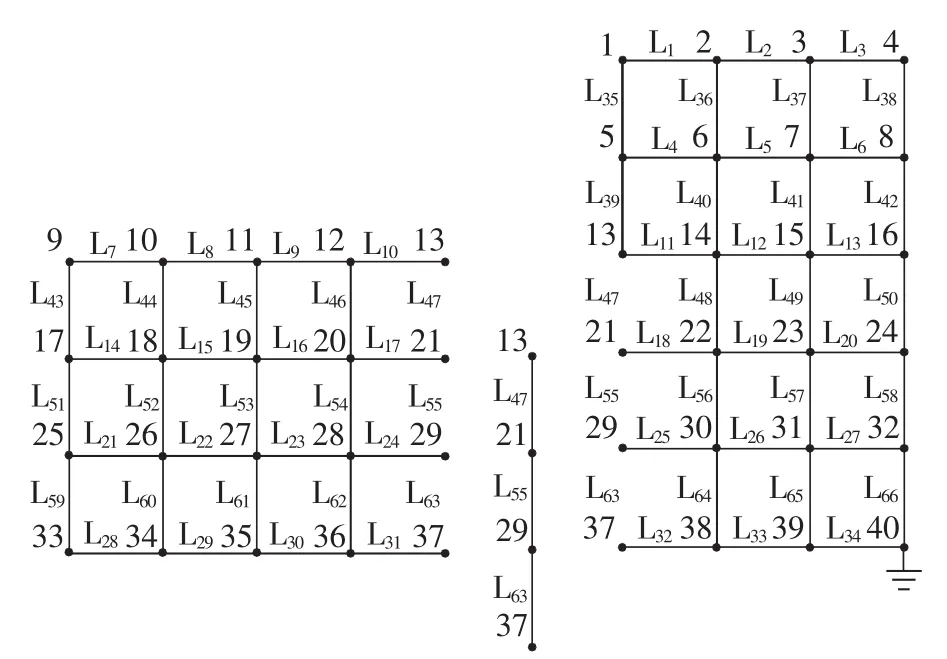
图4 子网络集和自由支路集Fig.4 Sub-grids and independent branches

按照图3在MATLAB中搭建仿真电路模型，将测量使用的电源模块参数设置为20 A的直流激励。首先分别在节点11与21间、11与29间、10与27间、18与33间、33与37间施加激励，测试节点10、11、13、18、21、27、33、37 的电压，得到第一个子网络的测试数据；然后在节点2与8间、8与21间、14与37间、16与21间、16与37间施加激励，测试得到节点2、3、6、8、13、14、16、21、23、29、30、39 的电压得到第二个子网络的数据；最后在节点13与29间、21与37间、8与18间、10与16间施加激励，得到自由支路集的测试数据。将测试得到的数据利用本文方法重复进行3次故障诊断，诊断结果基本一致。

接地网各个支路电阻的标称值、实际值、诊断值，以及实际值相对标称值的倍数p1、诊断值相对标称值的倍数p2如表1所示。

利用仿真得到可及节点电压值，通过改进化学反应优化算法求解，即可得到接地网电阻参数值。为了更加直观地表达本文的诊断结果，诊断结果采用如图5、图6所示的柱状图表示，图中横坐标为电路支路的编号，纵坐标为诊断结果电阻相对实际值增大的倍数。通过分析，改进化学反应优化算法得到的p2大部分在±0.45之间，但在支路L8、L23和L45处得到的倍数与实际故障倍数偏差稍大，分别是0.85、0.74、2.12。上述3条支路的诊断结果与实际值比较虽然相差较大，但也能基本反映接地网的实际情况，本文所提改进化学反应优化算法比较适合于大型接地网的故障诊断。

为了验证本文算法的准确性和有效性，仿真实验采用同样的仿真电压数据，同时运用禁忌搜索算法以及化学反应优化算法和本文算法进行故障诊断，仿真实验中禁忌搜索算法参数设置具体见文献［10］，化学反应优化算法参数设置见文献［15］。

表1 接地网支路实际状态和诊断结果Table1 Actual and diagnostic values of grounding grid branches

图5 接地网实际腐蚀情况Fig.5 Actual corrosion condition of grounding grid

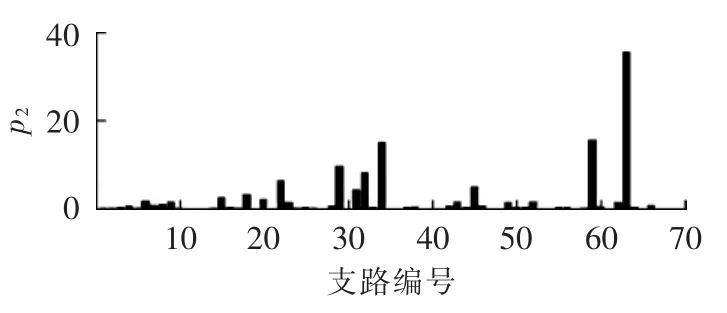
图6 改进化学反应优化算法诊断结果Fig.6 Diagnostic results by improved CRO algorithm

对比图7—9可以发现，在同样的实验条件和电压测试数据下，采用禁忌搜索算法和化学反应优化算法进行诊断的准确率不理想且误差偏大，而采用改进化学反应优化算法进行诊断的准确率高且误差较小。

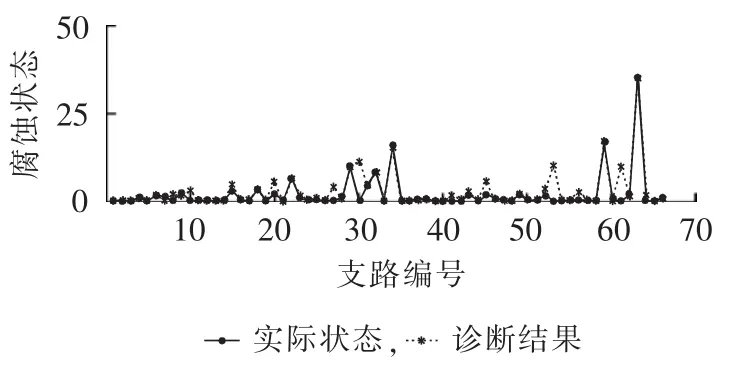
图7 禁忌搜索算法的诊断结果与接地网实际状态的比较Fig.7 Comparison between diagnostic result by tabu search algorithm and actual states of grounding grid

图8 化学反应优化算法的诊断结果与接地网实际状态的比较Fig.8 Comparison between diagnostic results by CRO algorithm and actual states of grounding grid

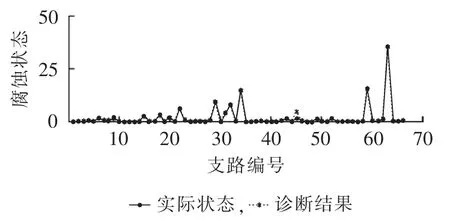
图9 改进化学反应优化算法的诊断结果与接地网实际状态的比较Fig.9 Comparison between diagnostic results by improved CRO algorithm and actual states of grounding grid

为了测试本文所提改进化学反应优化算法的性能表现，利用算例比较上述3种算法。连续运行3种算法各50次后，诊断结果对比如表2所示。

表2 3种算法的诊断结果对比Table2 Comparison of diagnostic results among three algorithms

考虑到实际接地网中可能存在支路导体缺失的情况，为了提升算法的实际应用价值，本文研究了接地网导体缺失对算法准确性的影响。

某支路导体缺失，理论上可以认为其支路电阻值为无穷大。仿真实验采用相同的接地网拓扑结构和激励测试方法。假设支路L7、L19、L29导体缺失，在其他条件不变的情况下，设定这3条支路的导体电阻值为无穷大。采用本文所提改进化学反应优化算法对有导体缺失和无导体缺失2种情况进行算例仿真，分别连续运行50次，结果如表3所示。

表3 有无导体缺失情况下的诊断结果对比Table3 Comparison of diagnostic results between with and without conductor loss

由表3可以看出，接地网导体的缺失虽然在一定程度上降低了本文所提改进化学反应优化算法的准确率，但准确率相对而言依旧较高，能够满足工程要求。需要指出的是，接地网导体缺失情况具有随机性，本文只模拟仿真了接地网导体缺失的一种情况，而对导体缺失的其他情况，以及其对接地网腐蚀故障诊断带来的影响、影响的原因和如何减小影响，有待进一步研究。

4 结论

本文将虚拟分子理论、化学反应优化算法和混沌插值算法有机结合，提出了基于节点撕裂和改进化学反应优化算法的接地网故障诊断方法。运用MATLAB对实际算例进行仿真比较，并得出如下结论：

a.利用虚拟分子理论优化接地网多目标故障诊断模型，将多目标求解问题转换成单目标求解问题，能有效降低全网络优化求解的计算量，进一步提高计算效率；

b.优化求解时，综合化学反应优化算法与Logistic映射的优点，并引入混沌策略，提出了改进化学反应优化算法，实现了较准确的全局寻优；

c.通过实例计算与仿真分析发现，本文算法较基于禁忌搜索算法、基本化学反应优化算法的接地网故障诊断方法而言具有更高的准确性和有效性。

［1］蔡崇积.电力交流接地网损坏原因调研与分析［J］.电力设备，2005，6（4）：20-22.CAI Chongji.Investigation and analysis on damage reasons of AC electric power grounding network［J］.Electrical Equipment，2005，6（4）：20-22.

［2］雷将锋，彭敏放，沈美娥，等.基于云遗传算法的接地网优化设计［J］.电力自动化设备，2012，32（7）：119-123.LEI Jiangfeng，PENG Minfang，SHEN Meie，et al.Optimal design of grounding grid based on cloud genetic algorithm［J］.Electric Power Automation Equipment，2012，32（7）：119-123.

［3］罗隆福，向博，许加柱，等.10 kV小电阻接地系统单相接地故障时的跨步电压仿真与实验研究 ［J］.电力自动化设备，2013，33（6）：22-26.LUO Longfu，XIANG Bo，XU Jiazhu，et al.Simulation and test of step voltage caused by single-phase grounding fault of 10 kV system earthed with low resistance［J］.Electric Power Automation Equipment，2013，33（6）：22-26.

［4］刘洋，崔翔，赵志斌，等.基于电磁感应原理的变电站接地网腐蚀诊断方法［J］.中国电机工程学报，2009，29（4）：97-103.LIU Yang，CUI Xiang，ZHAO Zhibin，et al.Method of corrosion diagnosis of substations’grounding grids based on electromagnetic induction theory［J］.Proceedings of the CSEE，2009，29（4）：97-103.

［5］张秀丽，骆平，莫逆，等.接地网腐蚀状态电化学检测系统的开发与应用［J］.中国电机工程学报，2008，28（19）：152-156.ZHANG Xiuli，LUO Ping，MO Ni，et al.Development and application of electrochemical detection system for grounding grid corrosion state［J］.Proceedings of the CSEE，2008，28（19）：152-156.

［6］杨滔，彭敏放，沈美娥，等.应用准稳态测量及小波变换的接地网腐蚀检测［J］.仪器仪表学报，2011，32（9）：2132-2138.YANG Tao，PENG Minfang，SHEN Meie，et al.Corrosion detection of grounding grids using quasi-steady-state measurement and wavelet transform ［J］.Chinese Journal of Scientific Instrument，2011，32（9）：152-156.

［7］许磊，李琳.基于电网络理论的变电站接地网腐蚀及断点诊断［J］.电工技术学报，2012，27（10）：270-276.XU Lei，LI Lin.Fault diagnosis for grounding grids based on electric network theory［J］.Transactions of China Electrotechnical Society，2012，27（10）：270-276.

［8］刘渝根，骆仁意，尚龙龙，等.基于遗传算法的电压法和电阻法在地网导体缺失诊断中的性能对比［J］.电力自动化设备，2014，34（10）：121-127.LIU Yugen，LUO Renyi，SHANG Longlong，et al.Comparison of performance between voltage and resistance methods in GA-based diagnosis for conductor loss in grounding grid［J］.Electric Power Automation Equipment，2014，34（10）：121-127.

［9］张英娇，罗先觉，牛涛，等.基于约束总体最小二乘算法的接地网故障诊断新模型［J］.西安交通大学学报，2010，44（10）：110-115.ZHANG Yingjiao，LUO Xianjue，NIU Tao，et al.New model of corrosion diagnosis for grounding grids based on constrained total least square algorithm［J］.Journal of Xi’an Jiaotong University，2010，44（10）：110-115.

［10］程红丽，刘健，王森，等.基于禁忌搜索的接地网故障诊断［J］.高电压技术，2007，33（5）：139-142.CHENG Hongli，LIU Jian，WANG Sen，et al.Fault diagnosis for grounding grids based on tabu search ［J］.High Voltage Engineering，2007，33（5）：139-142.

［11］刘渝根，腾永禧，陈先禄，等.接地网腐蚀的诊断方法研究［J］.高电压技术，2004，30（6）：9-21.LIU Yugen，TENG Yongxi，CHEN Xianlu，et al.A method for corrosion diagnosis of grounding grid［J］.High Voltage Engineering，2004，30（6）：19-21.

［12］罗先觉，范丽娟.模拟电路子网络级的故障定位［J］.西安交大学学报，1989，23（2）：1-8.LUO Xianjue，FAN Lijuan.Fault location of analog circuits at sub-network level［J］.Journal of Xi’an Jiaotong University，1989，23（2）：1-8.

［13］刘利强，罗先觉，王森，等.接地网腐蚀分块诊断的混合优化算法［J］.中国电机工程学报，2009，29（7）：33-38.LIU Liqiang，LUO Xianjue，WANG Sen，et al.Hybrid optimal algorithm for corrosion diagnosis for grounding grids ［J］.Proceedings of the CSEE，2009，29（7）：33-38.

［14］张智晟，温令云，李国，等.基于改进化学反应优化算法的电动汽车与可再生能源多目标协同调度［J］.电网技术，2014，38（3）：633-637.ZHANG Zhisheng，WEN Lingyun，LI Guo，et al.Multi-objective coordinated scheduling of electric vehicles and renewable generation based on improved chemical reaction optimization algorithm［J］.Power System Technology，2014，38（3）：633-637.

［15］LAM A Y S，LI V O K.Chemical-reaction-inspired metaheuristic for optimization［J］.IEEE Transactions on Evolutionary Computation，2010，14（3）：381-399.

［16］LAM A Y S，LI V O K.Real-coded chemical reaction optimization［J］.IEEE Transactions on Evolutionary Computation，2012，16（3）：339-353.

［17］王淳.基于化学反应算法的配电网重构［J］.电网技术，2012，36（5）：209-214.WANG Chun.Distribution network reconfiguration based on chemical reaction optimization ［J］.Power System Technology，2012，36（5）：209-214.

［18］ALATAS B，AKIN E，OZER A B.Chaos embedded particle swarm optimization algorithms［J］.Chaos，Solitons ＆ Fractals，2009，40（4）：1715-1734.

［19］柴秀丽，李伟，史春晓，等.基于超混沌系统的彩色图像加密新算法［J］.传感器与微系统，2013，32（8）：131-138.CHAIXiuli，LIWei，SHIChunxiao，etal.Novelencryption algorithm for color image based on hyperchaotic systems ［J］.Transducer and Microsystem Technologies，2013，32（8）：131-138.