双回并行直流输电谐波不稳定判据研究及改进

丁媛媛 ，刘天琪 ，周胜军 ，乔光尧 ，李兴源 ，王文慧

（1.四川大学 电气信息学院，四川 成都 610065；2.国网智能电网研究院，北京 102211）

0 引言

由于高压直流输电（HVDC）系统具有传输容量大、损耗低、快速、控制灵活等优点，在我国“西电东送”中得到了广泛的应用，随着区域间电网联系的紧密，电网将出现交直流并联系统和多馈入交直流系统的格局［1-5］。其中，同塔双回高压直流输电系统具有提高单位走廊的输送容量、提高通道利用率、节约土地资源等优点，已在我国投入运行［6］。

随着高压直流输电系统投入越来越多，对高压直流输电系统的分析和研究也愈发重要。当直流系统与弱交流系统相连接时，会带来电压不稳定、暂态不稳定、动态过电压、谐波不稳定等问题［7］。现代高压直流输电系统普遍采用等间隔脉冲触发方式，在换流变压器的参数和交流电压三相对称的情况下，引起谐波不稳定的因素主要为铁芯饱和与互补谐振，两者往往同时出现，互相影响。目前已发现4个系统发生过此类型的不稳定，分别是Kristiansand、Nelson River、New England 和 Chateauguay 直流系统［8］。

文献［9］基于矢量表达形式的换流器产生的负序直流电流，根据其表达形式中饱和稳定判定因子这一参数来判断系统是否会发生谐波不稳定；文献［10］基于特征值方法对高压直流输电中谐波不稳定进行分析；文献［11］提出了基于交流正负序阻抗和直流阻抗来判断系统是否会发生铁芯饱和谐波不稳定；文献［6］在文献［11］的基础上提出了基于交流正负序阻抗和直流阻抗的工程判据来判断双回并行高压直流输电系统是否发生谐波不稳定。

本文将直流偏磁效应系数加入谐波不稳定工程判据中，同时考虑双回直流线路阻抗的矢量值不同，提出新的双回直流线路的谐波不稳定工程判据，并在PSCAD进行中仿真验证，同时对比分析双回并行直流线路的谐波不稳定工程判据，仿真结果表明本文所提判据具有一定的参考价值。

1 谐波不稳定简介

直流输电引起的谐波不稳定是指在换流站附近有扰动时，谐波振荡不易衰减甚至放大的现象，主要表现为换流站交流母线电压严重畸变［7］。谐波不稳定发生时，谐波电流将会被放大几倍甚至几十倍，这对电力系统的危害是极其严重的，特别是对换流变压器、电抗器、电容器等元件造成很大威胁。谐波电流过大会造成电压的畸变，而电压畸变严重会引起换相失败，使直流输电系统运行困难甚至闭锁。

谐波不稳定主要由换流变压器铁芯饱和的直流偏磁效应和交直流侧频率互补谐振共同作用，谐波在传递过程中形成一个正反馈，造成谐波不断放大，导致换流站交流母线电压严重畸变。

1.1 开关函数理论

文献［11］中采用开关函数法分析了谐波在换流器之间的传递规律，即交流侧的正序二次谐波经过换流器作用后，在直流侧调制成一个基频谐波；直流侧的基频谐波经过换流器的调制作用后，可以分解成一个正序二次谐波和负序零次谐波，其中直流侧谐波传递到交流侧的关系如式（1）所示，交流侧谐波传递到直流侧的关系如式（2）所示。

1.2 直流偏磁效应

换流变压器铁芯饱和造成的直流偏磁效应［12］主要由变压器绕组的磁化特性曲线的饱和特性决定。如图1所示，当通过变压器的电流突然叠加一个直流电流后，在左侧上图中实线的基础上叠加了一个直流电流，得到点划线部分，即新的磁通变化曲线，此时，对应变压器的磁化曲线，变压器可能工作在它的磁饱和区域，引起感应电流的畸变，产生谐波电流，如右侧下图中点划线所示。换流变压器在直流偏磁的影响下，成为一个谐波源，从而加剧了谐波的放大。

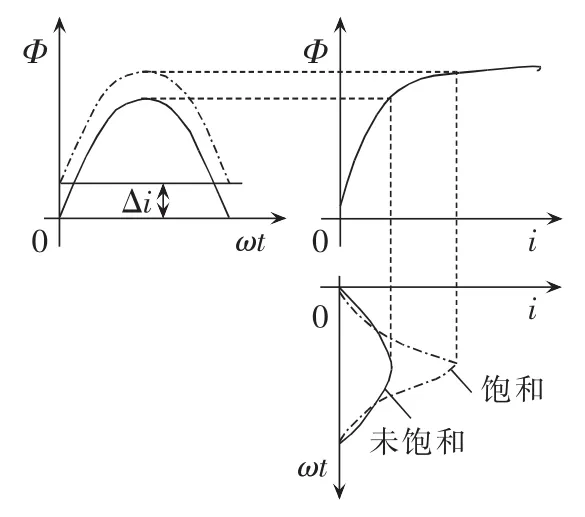
图1 换流变压器饱和直流偏磁原理图Fig.1 Schematic diagrams of saturated DC magnetic bias of converter transformer

1.3 谐波不稳定机理

Yacamini和 Oliveria［13］提出互补谐振理论，即交流侧和直流侧的互补谐振是指当交流侧的并联谐振频率fac与直流侧的串联谐振频率fdc满足式（3）所示关系时，就有可能会发生谐波不稳定现象。

其中，f1为交流侧系统基波频率；p为换流器的脉动数；K为自然数。

谐波不稳定主要表现为低次谐波的不稳定［14］，如图2所示，假设交流侧存在由一个很小的二次谐波分量引起的二次谐波谐振，这种谐波放大可能会导致在换流器的直流侧产生一个基频电压分量，该基频分量会反过来在换流变压器的阀绕组侧产生直流分量和二次分量，该直流分量会导致换流变压器铁芯饱和，进一步产生二次谐波（当然也会产生其他频率的谐波），这样就形成了一个正反馈，加剧了谐波的放大，并最终导致系统失稳。

图2 铁芯饱和不稳定形成原理Fig.2 Mechanism of harmonic instability due to core saturation

2 基于阻抗矢量性的双回并行线路谐波不稳定判据

在双回直流线路分析中，本文不考虑直流线路之间的相互作用，其谐波在双回直流线路中的传递过程如图3所示。

图3 双回并行HVDC系统中谐波传递的过程Fig.3 Process of harmonic transfer in parallel double-circuit HVDC transmission system

在t时刻，谐波从直流线路1侧变换到交流侧系统，经过Δt后，在t+Δt时刻，谐波从交流侧变换回直流线路1侧和直流线路2侧，此时，谐波经过一次传递；再经过Δt后，在t+2Δt时刻，直流线路1侧和直流线路2侧的谐波传递到交流侧系统；和谐波经过一次传递时类似，再经过Δt后，在t+3Δt时刻，交流侧谐波再次经过换流器传递到直流线路1侧和直流线路2侧。如图3所示，再根据t+3Δt时刻，直流线路1侧和直流线路2侧的谐波情况来分别判断2条线路是否可能发生谐波不稳定。

假设初始t时刻，直流线路1中的初始基频谐波电流为 Idc1（1）（t），由电路原理出发，根据式（1）所示谐波从直流侧传递到交流侧的关系，考虑换流变压器直流偏磁效应，并假设变压器所产生的二次谐波电流分量和流入变压器直流电流之比为k，所以交流侧二次谐波电压分量可以表示为：

其中，（t）为t时刻交流侧负序零次谐波电压；为交流侧正序二次谐波阻抗；为交流系统侧负序零次谐波阻抗。

根据式（2），在t+Δt时刻谐波再从交流侧调制回直流线路1，有：

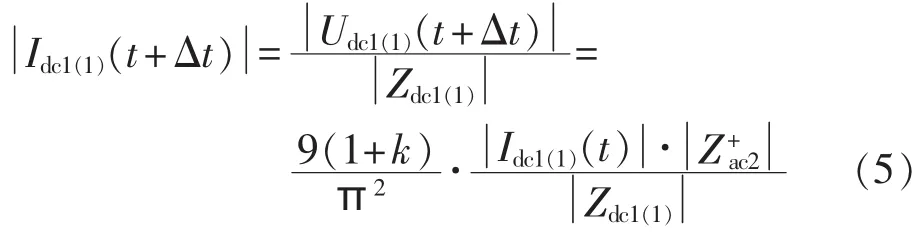
其中，Idc1（1）（t+Δt）为在 t+Δt时刻直流线路 1 中基频谐波电流值（下标中的前一个1代表直流线路1，后一个（1）代表基频谐波）；Zdc1（1）为直流线路 1 的基频谐波阻抗值；Idc1（1）（t）为初始 t时刻直流线路 1 中的基频谐波电流值。

同理，谐波从交流侧调制到直流线路2侧，有：

其中，Idc2（1）（t+Δt）为在 t+Δt时刻直流线路 2 中基频谐波电流值；Zdc2（1）为直流线路2的基频谐波阻抗值。

在t+2Δt时刻，交流侧谐波为直流线路1和2谐波调制到交流侧之和。此时考虑2条直流线路之间的电流值不同（幅值、相角），其等效原理如图3所示，同时考虑铁芯饱和问题，根据电路原理得：

其中，φ1、φ2分别为直流线路 1、2 的阻抗相位；Zdc1（1）、Zdc2（1）分别为直流线路1、2的基频谐波阻抗矢量值。

在t+3Δt时刻，谐波从交流侧传递到直流线路1，此时谐波电流为：

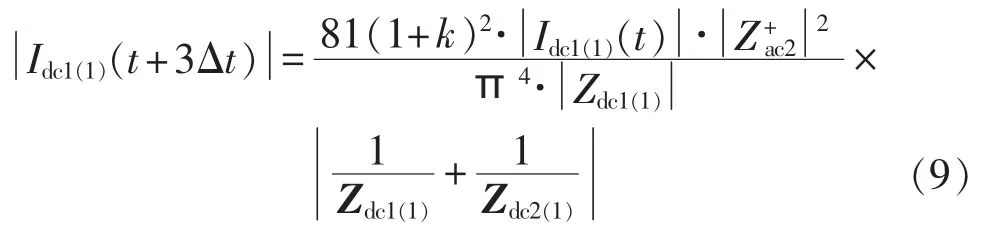
即使在最恶劣的情况下，式（9）的值也小于 1［15］，所以在此考虑最严重的情况，取 k=1［16］，当 t+3Δt时刻的电流和t时刻的电流之比大于等于1时，即说明谐波电流经过传递后被放大，系统不稳定，因此得出双回并行直流线路谐波不稳定的工程判据为：

因为是最保守估计，实际情况可能更为乐观，所以对于评估结果将通过故障时域仿真来校核。

3 算例分析

1994 年，Burton［17］率先提出了只含整流器的研究模型，1996 年，S.Chen［18］对该模型进行了改进，将直流侧电流源改成了电压源，换流站由定触发角控制改成了定电流控制。本文根据S.Chen改进模型，采用PSCAD/EMTDC建立双回并行直流线路系统的电磁暂态仿真模型，如图4所示。

图4 含整流器的双回直流线路模型Fig.4 Model of double-circuit HVDC transmission lines，containing rectifier

交流侧电压设定为100 kV，直流侧电压设定为100 kV，换流器控制采用CIGRE标准模型中的定电流控制，变压器参数如表1所示，系统参数设置如表2所示。

表1 变压器参数设置Table1 Parameter settings of transformer

表2 算例参数设置Table2 Parameter settings for study cases

在系统稳定的前提下，进行动态的频率扫描［19］分析，以获得送端系统的交/直流阻抗-频率特性。以算例1为例，得到交流侧和直流线路1和直流线路2的阻抗-频率扫描结果，如图5所示，取交流侧二次谐波阻抗值和直流侧基频谐波阻抗值代入判据可得谐波不稳定风险评估结果，同理可得算例2谐波不稳定的风险评估结果，如表3所示。

图5 算例1阻抗-频率扫描结果Fig.5 Impedance-frequency curves of Case 1

表3 双回直流线路谐波不稳定风险评估表Table3 Results of harmonic instability risk assessment for double-circuit HVDC transmission lines

由表3可知，算例1中直流线路1、2得到的风险评估值均为负，不满足发生谐波不稳定的判断条件；算例2中直流线路1、2的风险评估值均为正，有发生谐波不稳定的风险。因为是最保守估计，因此对于评估的结果，将通过电磁暂态故障仿真来校核。根据上述参数，对算例1、算例2进行电磁暂态仿真，结果分别如图6、图7所示（电流为标幺值）。

从图6中可以看出，算例1中直流线路1、2的直流侧电流在2 s故障后轻微振荡了一段时间，然后趋于稳定，这说明直流线路1、2都没有发生谐波不稳定，与判据得到的结论一致。

图6 算例1时域仿真结果Fig.6 Results of time-domain simulation for Case 1

图7 算例2时域仿真结果Fig.7 Results of time-domain simulation for Case 2

从图7中可以看出，算例2中直流线路1、2的直流侧电流在2 s时刻故障后维持大幅振荡，这说明直流线路1、2都发生谐波不稳定，与判据得到的结论一致。

4 判据对比分析

根据文献［6］所提出的判据为了统一它和本文所提的判据1的表达形式，做相应的数学变换，得到判据3；考虑正序二次谐波的主要作用，并加入双回并行直流线路的阻抗矢量不同这个因素，得到判据4；为了表现阻抗矢量和与数值和的差异，将本文所提出的判据1中的阻抗矢量和改成数值和，得到判据2。这4种判据形式如表4所示。

表4 4种双回直流线路谐波不稳定判据Table4 Four expressions of harmonic instability criterion for double-circuit HVDC transmission lines

在如表5所示的不同网络参数下，通过上述4种判据对是否发生谐波不稳定进行判断，并在PSCAD中进行电磁暂态仿真校核，当判断结果与仿真校验结果一致时说明判断正确，当判断结果与仿真校验结果不一致时说明判断错误。

4种判据的判断效果如表6所示。因为判据是最保守估计，因此电磁暂态仿真和评估结果可能会出现不一致，当仿真结果和判据结论不一致时，说明出现错误的判断。

根据表6可以看出，4种判据在本文模型中均有一定的准确性，在双回线路阻抗矢量存在相角差异时，本文所提出的判据更具有实用性。

同样由于判据是最保守估计，因此对于评估的结果需要通过电磁暂态故障仿真来校核。

5 结语

由于现有的一些利用阻抗-频率特性判断是否发生谐波不稳定的方法并没有充分利用阻抗-频率特性信息，所以在双回并行直流输电系统中，其工程判据还可以得到进一步提升。本文在现有双回并行直流输电线路谐波不稳定的基础上，引入了直流偏磁系数和双回直流线路的阻抗矢量差异，提出新的双回并行直流系统谐波不稳定的工程判据，并基于PSCAD仿真验证了本文提出的判据评估结论与电磁暂态故障仿真的结果吻合，表明该判据能较为准确地评估双回并行直流系统送端发生谐波不稳定的风险。并对比验证4种双回并行线路谐波不稳定判据，证明了本文所提出的判据具有一定参考价值。

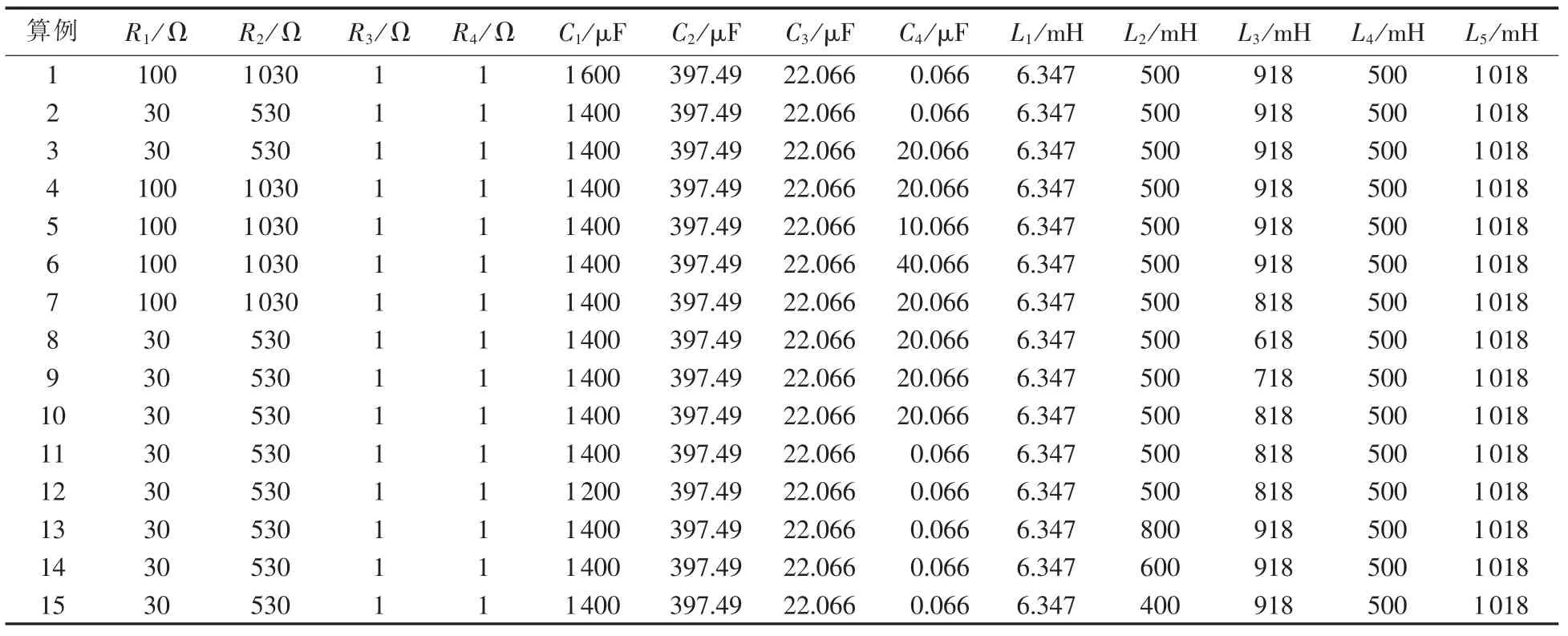
表5 算例参数设置Table5 Parameter settings for study cases

表6 4种判据评估比较Table6 Comparison of judgment among four criterions

［1］魏亮，王渝红，李兴源，等.高压直流输电送端孤岛运行附加频率控制器设计［J］.电力自动化设备，2016，36（1）：143-148.WEI Liang，WANG Yuhong，LI Xingyuan，et al.Design of additional frequency controller for islanded sending-end operation of HVDC system［J］.Electric Power Automation Equipment，2016，36（1）：143-148.

［2］李保宏，刘天琪，许韦华，等.直流参与受端弱交流系统黑启动的技术条件［J］.电力自动化设备，2016，36（5）：23-29.LI Baohong，LIU Tianqi，XU Weihua，et al.Technical conditions of HVDC for involving in black-start of weak receiving AC system［J］.Electric Power Automation Equipment，2016，36（5）：23-29.

［3］李妮，李兴源，冯明，等.改善多馈入直流系统电压无功特性的直流控制策略［J］.电力自动化设备，2016，36（2）：25-31.LI Ni，LI Xingyuan，FENG Ming，et al.DC control for improving voltage and reactive power characteristics of multi-infeed HVDC system［J］.Electric Power Automation Equipment，2016，36（2）：25-31.

［4］汤广福，罗湘，魏晓光.多端直流输电与直流电网技术［J］.中国电机工程学报，2013，33（10）：8-17.TANG Guangfu，LUO Xiang，WEI Xiaoguang.Multi-terminal HVDC and DC-grid technology［J］.Proceedings of the CSEE，2013，33（10）：8-17.

［5］徐政.含多个直流换流站的电力系统中交直流相互作用特性综述［J］.电网技术，1998，22（2）：18-21.XU Zheng.AC/DC and DC/DC interactions of multiple HVDC links terminating in the same AC system［J］.Power System Technology，1998，22（2）：18-21.

［6］穆子龙，李兴源，王渝红.两回HVDC并行输电系统送端谐波不稳定问题的判据研究［J］.电网技术，2012，36（11）：153-158.MU Zilong，LI Xingyuan，WANG Yuhong.Research on criterion for harmonic instability at sending end of HVDC transmission system composed of parallel double-circuit lines［J］.Power System Technology，2012，36（11）：153-158.

［7］李兴源.高压直流输电系统［M］.北京：科学出版社，2010：1-9，126-133.

［8］晏小彬.交直流互联系统铁心饱和谐波不稳定研究［D］.成都：四川大学，2013.YAN Xiaobin.Iron core saturation harmonic instability in AC/DC interconnected system［D］.Chengdu：Sichuan University，2013.

［9］陈浩，李琳，许正梅.换流变压器铁心饱和型不稳定性预测［J］.电工技术学报，2013，28（6）：108-113.CHEN Hao，LI Lin，XU Zhengmei.Prediction of core saturation instability at converter transformer［J］.Transactions of China Electrotechnical Society，2013，28（6）：108-113.

［10］陈宝亮，李兴源，穆子龙，等.基于特征值方法的高压直流输电中谐波不稳定分析［J］.华东电力，2012，40（6）：1022-1026.CHEN Baoliang，LI Xingyuan，MU Zilong，et al.Harmonic instability analysis for HVDC transmission system based on eigenvalue method［J］.East China Electric Power，2012，40（6）：1022-1026.

［11］樊丽娟，穆子龙，金小明，等.高压直流输电系统送端谐波不稳定问题的判据［J］.电力系统自动化，2012，36（4）：62-68.FAN Lijuan，MU Zilong，JIN Xiaoming，et al.Criterion of harmonic instability at sending end of HVDC power transmission system［J］.Automation of Electric Power Systems，2012，36（4）：62-68.

［12］董霞.变压器直流偏磁研究［D］.济南：山东大学，2013.DONG Xia.Study on the transformers under DC bias［D］.Ji’nan：Shandong University，2013.

［13］YACAMINI R，OLIVERIA J C.Instability in HVDC schemes at low-order integer harmonics［J］.IEE Proceedings-Generation，Transmission and Distribution，1980，127（3）：179-188.

［14］杨小兵，李兴源，金小明，等.基于调制理论的换流变压器铁心饱和不稳定分析［J］.电网技术，2009，33（20）：49-53.YANG Xiaobing，LI Xingyuan，JIN Xiaoming，et al.Modulation theory based analysis on converter transformer core saturation instability［J］.Power System Technology，2009，33（20）：49-53.

［15］桂重.高压直流输电系统铁芯饱和型谐波不稳定性研究［D］.武汉：华中科技大学，2007.GUI Zhong.Study on core saturation harmonic instability in an HVDC transmission system［D］.Wuhan：Huazhong University of Science&Technology，2007.

［16］魏玥，刘天琪，晏小彬，等.高压直流输电系统直流偏磁下的谐波不稳定判据研究［J］.电力系统保护与控制，2014，42（17）：139-144.WEI Yue，LIU Tianqi，YAN Xiaobin，et al.Study of harmonic instability criterion under DC magnetic bias in HVDC system［J］.Power System Protection and Control，2014，42 （17）：139-144.

［17］BURTON R S，FUCHSHUBER C F，WOODFORD D A，et al.Prediction of core saturation instability at an HVDC converter［J］.IEEE Transactions on Power Delivery，1996，11（4）：1961-1969.

［18］CHEN S，WOOD A R，ARRILLAGA J.HVDC converter transformer core saturation instability：a frequency domain analysis［J］.IEE Proceedings-Generation，Transmission and Distribution，1996，143（1）：75-81.

［19］周双亚，肖湘宁，郝君伟，等.频率扫描法在次同步振荡分析中的应用［J］.现代电力，2011，28（5）：1-5.ZHOU Shuangya，XIAO Xiangning，HAO Junwei，et al.Application of frequency scanning method in analyzing sub-synchronous oscillation［J］.Modern Electric Power，2011，28（5）：1-5.