基于节点状态优化的配电网故障恢复混合整数线性规划方法

刘宗歧，石道桂，陈 启，刘文霞

（华北电力大学 电气与电子工程学院，北京 102206）

0 引言

随着配电网结构的日趋复杂［1］和用户对电能依赖程度的不断提高，配电网故障恢复作为智能电网自愈控制的重要环节，是电网建设亟待完善的一项重要课题［2］。配电网故障恢复往往被认为是一个非线性、多约束的组合优化且NP（Non-deterministic Polynomial）难问题，在数学上还没有完美的解决方法［3］。 从计算方法上可分为数学优化法［4］、启发式搜索方法［5］、人工智能方法［6］及其组合方法［7］4 类。

传统研究认为，故障恢复就是通过对配电网的联络开关及分段开关进行操作，将断电负荷转移到其他馈线进行供电［8］，即开关状态决定了节点恢复情况（节点-电源连通状态，本文称为节点状态）。开关状态关联节点状态取决于配电网网络拓扑［9］特征，具有高度非线性，另外潮流本身的非线性特点，制约了故障恢复在线性规划方法上的突破。

本文转变研究思路，以节点状态为研究对象，分析节点状态参与故障恢复的应用条件，并建立基于节点状态的开关状态线性模型。运用线性化方法对节点注入电流进行等效，以此建立计及节点状态的故障恢复混合整数线性规划模型。算例围绕计算精度和计算效率进行仿真分析。

1 基于节点状态的配电网络拓扑建模

1.1 节点状态变量概念

类似于开关的闭合和断开两状态，节点状态在故障恢复问题中也可大致分为供电状态和失负荷状态，以图1进行描述。

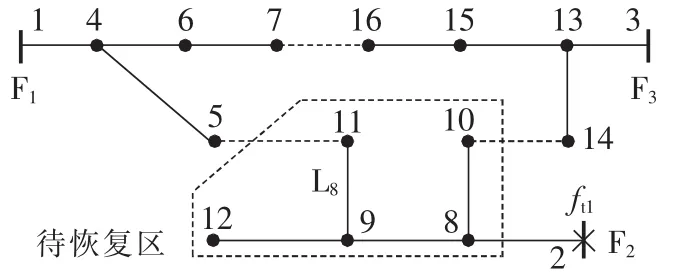
图1 典型三馈线配电系统Fig.1 Typical distribution system with three feeders

图1为简化的网络模型，只包含等值后的节点、母线及带可操作开关［10］的支路。正常运行时图1中电源各自带负荷；当电源F2发生永久性故障时，通过故障隔离形成包含节点 8、9、10、11、12 的待恢复区域，其他配电部分可定义为故障关联区域，即与待恢复区域有联络、并提供备用支持的区域。

节点状态变量，表示节点连通不同电源的情况，即节点可能的供电路径选项，为0-1整数变量，用ei，b表示，i为节点编号，b为电源编号。节点状态变量的个数与系统联络水平有关，比如节点11与3个电源都有关联路径，则其节点状态变量分别为 e11，1、e11，2、e11，3，正常运行状态下 e11，2=1，e11，1=e11，3=0；电源 F2发生故障时 e11，2=0，e11，1、e11，3为待优化的变量。

节点状态变量ei，b包含2个属性，其一为节点属性，对应编号i；其二为电源属性，对应编号b。

（1）节点属性。

节点属性具体是指节点与电源之间的电气距离，用于建立具有相同电源属性的节点状态变量之间的大小关系。图1中，节点11比节点9距离电源F1近，则 e11，1≥ e9，1。 节点属性描述为：

其中，di，b和 dj，b分别为节点 i、j与电源 b 的电气距离。

（2）电源属性。

首先定义表征节点是否恢复的变量ei：

其中，PS为电源集合。

电源属性是指节点至多只能由1个电源供电的属性，用于满足配电系统单辐射运行条件，即：

在故障恢复模型中支路电流取决于开关状态，并且故障恢复的开关操作次数也是优化目标，所以需建立基于节点状态的开关状态模型。

1.2 开关状态模型

以图1支路L8为例，其两端节点分别为节点11和9，而节点11侧电源为F1，节点9侧电源为F3（故障条件下），支路L8闭合的情况包括：

（1）节点9由节点11侧的电源F1转带；

（2）节点11由节点9侧的电源F3转带；

（3）节点9和节点11均未恢复供电，支路L8闭合使两端节点同时孤岛，即节点状态变量均为0。

由节点状态变量属性可知，以上3种开关闭合情况为互斥事件。为保证开关状态模型的通用性，作简图进行分析，如图2所示。

图2 支路简化图Fig.2 Simplified diagram of branch

图2中，xij为支路状态变量，取值0和1，分别表示开关断开和闭合；PSi和PSj分别表示i-j支路两端电源集合，两集合的并集为集合PS；b1和b2分别为集合 PSi和 PSj中的电源编号，则 ei，b1和 ei，b2分别为节点i关联 PSi和 PSj中电源的节点状态变量，ej，b1和 ej，b2类似。

概括3类互斥的开关闭合情况：

式（4）中（1-ei）（1-ej）展开的 eiej为非线性，考虑到变量ei和ej只能取值0和1的特点，可引入辅助变量wij=eiej，满足线性约束：

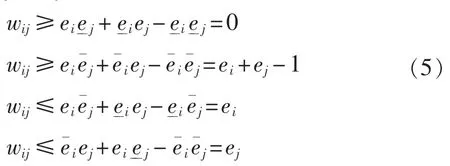
其中和分别为 ei的上、下限。

2 基于节点状态优化的故障恢复线性规划模型

典型线性规划数学模型［11］包含控制变量u、状态变量s、等式约束条件h、不等式约束条件g及目标函数f，如下式所示：

本文控制变量为节点状态变量ei，b，节点电压实部Ure和虚部Uim、支路电流实部Ire和虚部Iim等系统状态变量跟随节点状态变量。等式约束主要是指基尔霍夫电流及电压等式。

基尔霍夫电流等式为：

其中，i为待恢复区域及故障关联区域内节点编号；OT和IN均为与节点i相连的节点集合，分别表示关联节点i支路的电流流出节点和流入节点；和分别为支路k-i的支路电流实部和虚部；和分别为支路i-h的支路电流实部和虚部；和分别为节点i注入电流的实部和虚部。

基尔霍夫电压等式为：

其中，和分别为节点i电压的实部和虚部；Rik和Xik分别为支路i-k的电阻和电抗。

电流及电压等式均为线性，但是对于恒功率负荷，其节点注入电流是节点电压的非线性函数［12］：

其中，Pi和Qi分别为负荷注入节点i的有功和无功，对于恒功率负荷，Pi和Qi均为常数。

为满足线性规划建模要求，需对式（9）线性化。

2.1 节点注入电流线性化表达

采用分段线性化方法进行拟合，对于二元函数，可理解为分块线性化。以z=x/（x2+y2）为例，如图3所示。

图3 三维空间分块线性化Fig.3 Block linearization of 3D space

由图3可以看出，空间可行区域内任意一点都可由所在线性分块内的确定点来表达：

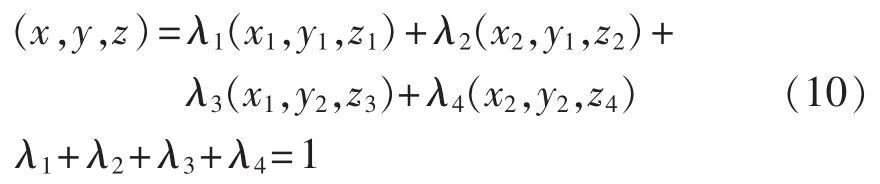
式（10）与文献［13］采用的第二类特殊序列集合SOS2（Special Ordered Sets of type 2）是一致的。 基于 SOS2，式（9）中的系数 ξi和 ζi线性化得到：

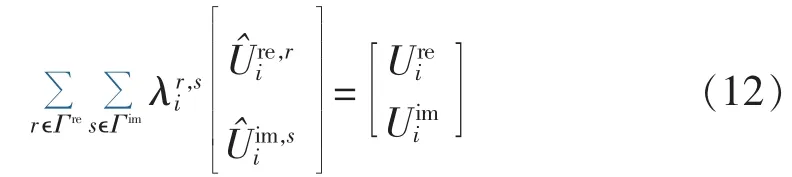
其中和分别为SOS2评估点集合，即空间线性分块确定的电压实部和虚部分段集合；为评估点的评估值。评估点的选择详见文献［13］，本文不再赘述。

2.2 计及节点状态的故障恢复潮流线性约束

由上述分析得到，节点注入电流由节点电压决定，考虑到待恢复区域节点状态的不确定性，对待恢复区域的节点电压约束进行松弛。

其中，和分别为节点i电压实部取值的上、下限；和分别为虚部的上、下限。

若采用式（11）—（13）线性化方法，式（13）修正为：

式（15）表示，ei=0 时，均为 0，那么线性拟合的节点注入电流为0。

同样，待恢复区域支路电流的松弛约束为：

其中，和分别为支路i-k的支路电流实部上、下限；和分别为虚部上、下限。

基尔霍夫电压等式需考虑支路断开的情况，以实部量为例，引入修正量Δre满足：

式（17）表示，当 xik=0，即支路 i-k 断开时，Δre的最小值为节点i失压时节点k电压上限的负数-Umax，最大值为节点k失压时节点i电压上限Umax；当xik=1 时，与式（8）一致。

待恢复区域、故障关联区域的节点电压约束为：

其中，Uimax和Uimin分别为节点i电压幅值的上、下限。

待恢复区域、故障关联区域支路的电流约束为：

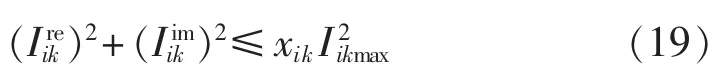
其中，Iikmax为支路i-k的支路电流幅值上限。

节点电压、支路电流越限约束中均包含二次非线性函数，且为可分离函数，方便运用分段线性化方法进行处理，以节点电压为例，可得：

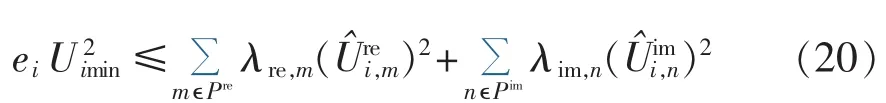
其中，Рre和Рim为分段线性化的评估点集合；和分别为评估点m和n的评估值。

2.3 基于节点状态优化的故障恢复目标

上述建立了故障恢复模型的等式约束及不等式约束线性模型，本节主要分析和建立故障恢复线性目标函数。

首先，最大限度地恢复受故障影响的负荷是故障恢复最主要的优化目标：

其中，FT为待恢复区域内节点集合。

其次，开关操作次数最少为另一目标：

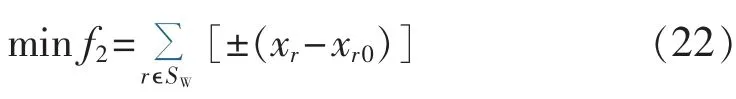
其中，SW为待恢复区域内开关集合；r为SW内开关；“±”对应开关初始状态，如果初始开关状态断开，即xr0=0，为体现xr0=1时开关操作，“±”取正，相反xr0=1 时，“±”取负。

配电网故障恢复的目标是最大限度恢复供电，而恢复后运行是否经济则是次要的［10］，开关操作次数目标只是在保证尽可能多的负荷恢复前提下其值尽可能小，所以目标f1应起到绝对支配作用，转化成单目标，如式（23）所示。

其中，系数λ为单目标权重，取较大值。

3 算例仿真分析

总结本文配电网故障恢复整数规划模型控制变量集合状态变量集合设置节点电压 SOS2 评估点：

线性规划不仅具有全局收敛的优点，并且易于通过商业化求解器仿真实现。本文算例在MATLAB仿真环境下运用整数规划工具箱进行建模求解。

3.1 算例1

首先，以图1典型三馈线配电系统作为测试系统，具体网络参数见文献［11］。其计算结果如表1所示。

由表1可以看出，节点电压及支路电流均被限制在安全范围内；潮流量计算结果相比于常规潮流方法偏差非常小，且每次计算结果一致，耗时较短。

表1 算例1计算结果Table1 Calculative result of Case 1

3.2 算例2

算例1测试系统为实际常见的不同电源馈线间联络的系统。本文模型同样适用于单馈线分支联络的系统，如图4所示的33节点系统［12］。

图4 33节点网络结构示意图Fig.4 Schematic diagram of 33-bus system

其计算结果如表2所示。

表2 算例2计算结果Table2 Calculative result of Case 2

同样，由表2可以看出，潮流量均在安全范围内，误差非常小，并且多次仿真实验显示不会出现误差堆积的情况；计算时间能够保证故障恢复的实时性，并且由于线性规划本身特性随着系统规模的增大，不存在维数灾的问题。优化结果即是最终故障恢复策略，不需要再进行潮流安全校验。

4 结论

本文从故障恢复线性规划建模角度，提出了节点状态变量概念，将配电网故障恢复问题转化为节点状态优化问题；基于节点状态的节点属性和电源属性，建立了开关状态线性模型，模型不受网络拓扑的限制；通过对节点注入电流线性等效建立了故障恢复混合整数线性规划模型，该模型具有最优潮流特点，并且易于计及分布式电源。最后，算例验证了开关状态线性模型及故障恢复线性规划模型的合理性及有效性。

［1］王守相，张一帆，葛磊蛟.新型城镇配电网影响因素解释结构模型［J］.电力自动化设备，2015，35（11）：75-81.WANG Shouxiang，ZHANG Yifan，GE Leijiao.Interpretative structural model of influencing factors for distribution network of new-type town［J］.Electric Power Automation Equipment，2015，35（11）：75-81.

［2］臧天磊，钟佳辰，何正友，等.基于启发式规则与熵权理论的配电网故障恢复［J］.电网技术，2012，36（5）：251-257.ZANG Tianlei，ZHONG Jiachen，HE Zhengyou，et al.Service restoration of distribution network based on heuristic rules and entropy weight［J］.Power System Technology，2012，36（5）：251-257.

［3］吴文传，张伯明.基于待恢复树切割的配电网故障恢复实时算法［J］.电力系统自动化，2003，27（12）：50-54.WU Wenchuan，ZHANG Boming.A candidate restoring tree cutting based algorithm for real-time distribution system restoration［J］.Automation of Electric Power Systems，2003，27（12）：50-54.

［4］张浩，和敬涵，薄志谦，等.基于动态规划算法的故障恢复重构［J］.电工技术学报，2011，26（12）：162-167.ZHANG Hao，HE Jinghan，BO Zhiqian，et al.Service restoration based on dynamic programming［J］.Transactions of China Electrotechnical Society，2011，26（12）：162-167.

［5］张海波，张晓云，陶文伟.基于广度优先搜索的配电网故障恢复算法［J］.电网技术，2010，34（7）：103-108.ZHANG Haibo，ZHANG Xiaoyun，TAO Wenwei.A breadth-first search based service restoration algorithm for distribution network［J］.Power System Technology，2010，34（7）：103-108.

［6］卢志刚，董玉香.基于改进二进制粒子群算法的配电网故障恢复［J］.电力系统自动化，2006，30（24）：39-43.LU Zhigang，DONG Yuxiang.Distribution system restoration based on improved binary particle swarm optimization［J］.Automation of Electric Power Systems，2006，30（24）：39-43.

［7］巩伟峥，房鑫炎.基于混合编码方式的配电网故障恢复算法研究［J］.电力系统保护与控制，2012，40（6）：104-108.GONG Weizheng，FANG Xinyan.Research of distribution system service restoration algorithm based on hybrid encoding［J］.Power System Protection and Control，2012，40（6）：104-108.

［8］刘莉，陈学锋，翟登辉.智能配电网故障恢复的现状与展望［J］.电力系统保护与控制，2011，9（13）：148-154.LIU Li，CHEN Xuefeng，ZHAI Denghui.Status and prospect of service restoration in smart distribution network［J］.Power System Protection and Control，2011，9（13）：148-154.

［9］兰剑，王东旭，叶曦，等.故障线路单端跳闸条件下节点电压暂降幅值计算方法［J］.电力自动化设备，2014，34（8）：78-82.LAN Jian，WANG Dongxu，YE Xi，et al.Calculation of voltage sag amplitude for single-terminal trip of faulty line［J］.Electric Power Automation Equipment，2014，34（8）：78-82.

［10］张锋，江道灼，张怡.基于变结构耗散网络的特殊配电网接线故障恢复的改进算法［J］.电网技术，2003，27（4）：49-53.ZHANG Feng，JIANG Daozhuo，ZHANG Yi.A improved algorithm special distribution network connection service restoration based on variable structure dissipated net theory ［J］.Power System Technology，2003，27（4）：49-53.

［11］吕蓬，潘志.运筹学·数学规划篇［M］.北京：清华大学出版社/北京交通大学出版社，2011：9.

［12］BORGHETTI A.A mixed-integer linear programming approach for the computation of the minimum-losses radial configuration of electrical distribution networks［J］.IEEE Transactions on Power Systems，2012，27（3）：1264-1273.

［13］RAFAEL S F，CARMEN L T B，MARIO V F P.A flexible mixed-integer linear programming approach to the AC optimal power flow in distribution systems［J］.IEEE Transactions on Power Systems，2014，29（4）：2447-2459.

［14］刘健，董新洲，陈星莺.配电网故障定位与供电恢复［M］.北京：中国电力出版社，2012：9-23.

［15］CIVANLAR S，GRAINGER J J，YIN H，et al.Distribution feeder reconfiguration for loss reduction［J］.IEEE Transactions on Power Delivery，1988，3（3）：1217-1223.

[16］BARAN M E，WU F F.Network reconfiguration in distribution systems for loss reduction and load balancing［J］.IEEE Power Engineering Review，1989，9（4）：101-102.