基于KPCA-KMPMR的短期风电功率概率预测

李 军，常燕芝

（兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070）

0 引言

随着风电场风电装机容量的不断攀升，风电在电力系统中高度渗透。然而由于风能的随机性和间歇性，风电场的发电输出功率往往很难控制。因此，大规模风电并网给电网计划和调度、电网的稳定性以及电能供应的可靠性等方面带来挑战。精确、可靠的风电功率预测对于优化电网运行的成本和提高电力系统的可靠性极其重要［1-2］。短期风电功率预测能够规避由于风电机组装机容量的增大而带来的风电功率波动性的影响，是能源领域非常重要的研究方向之一。

风电功率的预测方法通常分为物理方法、统计方法、基于计算智能的学习方法等［3-4］。借助计算智能的方法，如小波分析、神经网络、支持向量机（SVM）等，能从风电功率的历史时间序列中描述输入与输出的非线性关系，在风电功率超短期与短期预测中能取得较好的预测效果［5-10］。但就现有的短期风电功率预测方法而言，前馈神经网络方法存在网络结构难以确定、易陷入局部极小、“过拟合”等不足，且其基于梯度下降的训练也使得算法的复杂度较高。

SVM方法具有很好的泛化能力，解决了“过拟合”问题，但在算法实现上需求解复杂的全局二次凸优化问题。其他如小波分析与神经网络结合的方法在数据的特征提取上有所改进，但也存在算法的实现复杂、计算量较大的问题。另外，目前的大多数研究仅聚焦于给出预测期望值的点预测技术，由于风电功率预测的不确定性误差是不可避免且有意义的。因而，在提高预测精度的同时，若能给出预测不确定性误差的范围，则有助于评估依赖预测结果的决策风险。文献［11］尝试通过对风电功率预测误差分布特性的研究，实现了一定置信水平下风电功率的波动区间估计。

核最小最大概率分类机（KMPMC）［12］作为一种概率核学习方法，能最小化分类器的最大误判概率。核最小最大概率回归机（KMPMR）［13］建立在其基础上，将回归建模问题看作概率建模的一种形式，对模型的分布不作具体假设，仅需给定模型数据分布的均值与协方差矩阵，能够最大化模型的预测输出位于其真实值边界内的最小概率。与前馈神经网络、SVM等方法的求解不同，KMPMR方法仅涉及矩阵运算，基于KMPMC求解回归建模问题，计算效率高，尤其是在预测输出的同时，还能够给出预测误差分布的范围。文献［14］给出KMPMR结合遗传进化的方法成功应用于地震超声衰减预测的实例。因此，为解决现有风电功率预测方法的不足，可考虑将KMPMR方法用于短期风电功率概率预测中。另一方面，非监督的学习方法——核主成分分析（KPCA）［15-16］可在高维核特征空间进行数据的特征提取，与主成分分析（PCA）不同，它能有效地提取数据的非线性特征，同样可考虑将其用于短期风电功率预测的数据预处理中，以进一步提高预测精度。

由以上分析可知，结合KPCA和KMPMR各自的优点，针对短期风电功率预测，提出基于KPCA-KMPMR的概率预测方法，并给出相应的算法实现。将所提出方法应用于不同地区的风电功率预测实例中，在同等条件下，还与单一的KMPMR、SVM等预测方法进行比较，以验证所提出方法的有效性。

1 KPCA-KMPMR方法

PCA是一种广泛采用的特征提取方法，它仅涉及在数据的原始空间上进行线性化处理的技术。KPCA作为一种非监督技术，它是原始输入数据经变换后在高维非线性特征空间上执行线性PCA的方法。本文将KPCA方法用于短期风电功率时间序列预测模型的输入预处理中，按照相关度选取非线性特征作为预测模型的输入。

1.1 KPCA方法

KPCA与其他类型的非线性PCA方法不同，它是利用核技术将低维空间的数据映射到高维特征空间后，通过线性代数在特征空间执行主元的提取。

将训练数据 xi（i=1，2，…，l；xi∈Rn）通过非线性映射映射到 N 维特征空间中，构成 l×N 维的矩阵 X=［φ（x1） φ（x2） … φ（xl）］T。

数据预先经过中心化处理或具有零均值，则其协方差矩阵∑可表示为：l∑=XTX，其元素为：

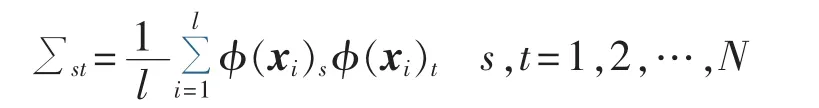
类似地，定义核矩阵K=XXT，则其元素为Ki，j=k（xi，xj）=φT（xi）φ（xj）。首先对核矩阵 K 与协方差矩阵∑分别进行特征值分解，则有：

其中，正交矩阵V的列vi为K的特征向量；正交矩阵U的各列形成的向量ui为l∑的特征向量。

利用K与l∑的对称性，能将l∑的任意特征向量u与特征值λ，变换为K所对应的特征向量Xu与特征值 λ。令 t=rank（XXT）=rank（XTX）≤min（N，l），则U的前t列特征向量构成的矩阵Ut可表示为：

其中，假定K与l∑的前t个非零特征值是按降序排列的。

由式（2）可知，l∑ 的第j个特征向量 uj具有一种相应的对偶表示，即可由核矩阵K的相应特征向量 vj乘以尺度化因子系数，如式（3）所示。

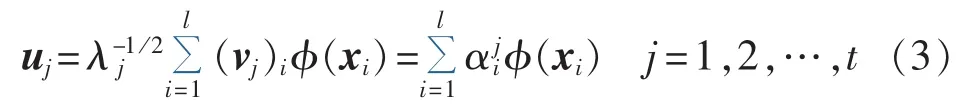
其中，向量 uj的对偶变量分别为 K的第j个特征向量及对应的特征值；为 αj的第i个元素。

考虑式（3），若定义Ud是特征空间中由前d个特征向量ud所张成的子空间，训练数据φ（x）在该子空间上的d维向量投影为：

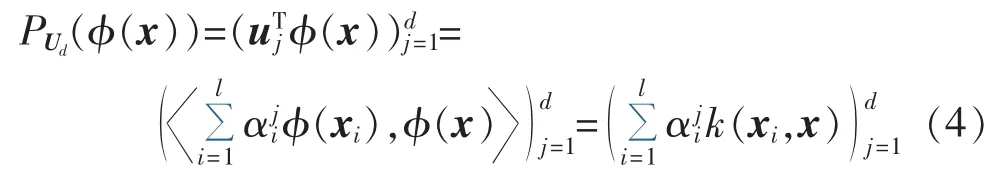
其中，〈·，·〉为内积符号。

式（4）即KPCA方法的核心。本文中，将使用最常见的高斯核函数，其形式为：

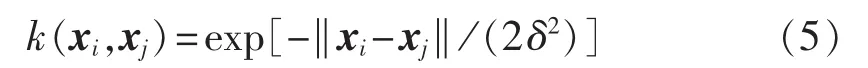
其中，δ为高斯核函数的宽度。

具体的KPCA算法实现步骤如下。

a.计算 X=［φ（x1） φ（x2） … φ（xl）］T所形成的核矩阵 K，其元素 Kij=k（xi，xj）（i，j=1，2，…，l）。

b.对核矩阵K进行中心化处理：

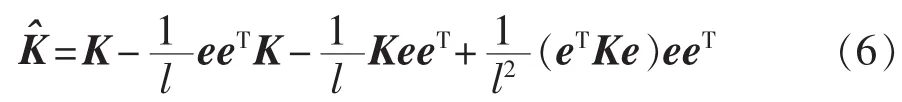
其中，e为所有元素均为1的列向量。

c.由式（1）对核矩阵进行特征值分解：

其中，eig（）为MATLAB函数，表示对矩阵进行特征值分解。

d.由式（3）计算前d个特征向量v的相应对偶向量表示，即计算前d个对偶向量α：

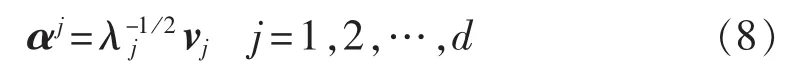
e.在核空间上，计算训练数据φ（x）在前d个对偶特征向量上的投影，即计算非线性主元如下：

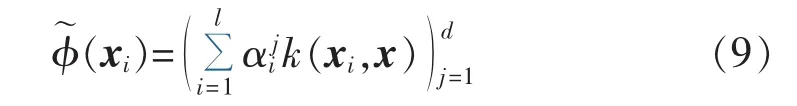
由式（9）可知，KPCA方法最多可提取的非线性主元数目为训练样本的数目l。将特征值按照降序排列，可选取前 d 个主元（d≤l），即（xi）⊆Rd，因此，KPCA方法的算法复杂度为O（dl2）。

1.2 KMPMR方法

KMPMR回归方法是非线性核空间下KMPMC分类方法用于回归问题的延伸。若给定的训练样本集分别服从于均值为、协方差为∑x以及均值为的某种有界分布Λ，且由如下的理想回归模型产生：

其中，噪声项 ρ的均值 E［ρ］＝＝0，方差 Var［ρ］＜∞为有限数。将xi映射到高维非线性特征空间后，用f（x）逼近式（10）的 f*（x），由表示定理［17］可知：

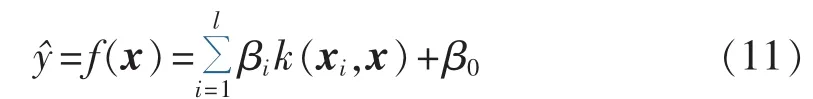
其中，βi，β0∈R；k（xi，x）=Φi（x）为满足 Mercer条件的核函数。

式（11）逼近式（10）的目标是最大化其模型输出位于真实输出值 y±ε（ε∈R，ε＞0）管道内的最小概率下界，即。该误差界的计算需要考虑由核函数构成的向量 Φ=（Φ1，Φ2，…，Φl）作为随机变量所形成的分布，即：

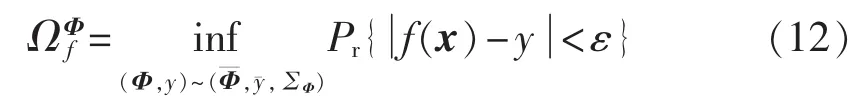
其中，、∑Φ＝cov（y，Φ1，Φ2，…，Φl）分别为由核函数与模型输出联合构成的随机向量所形成均值与协方差矩阵；Pr｛·｝表示求概率。KMPMR回归方法的求解将基于KMPMC的框架进行。为此，需将训练样本集转换为特定的二分类问题，即：

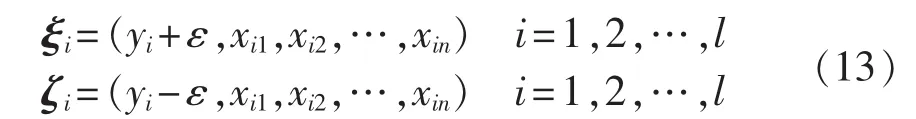
其中，ξi，ζi∈Rn+1。将 2 类样本通过非线性映射函数映射至高维特征空间，即：

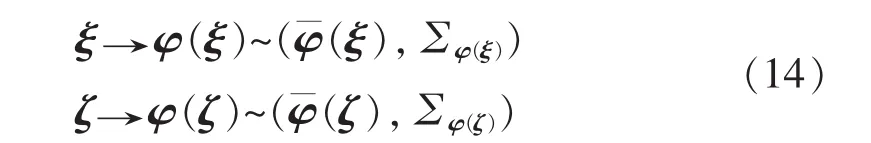
其中，（（ξ），∑φ（ξ））与（（ζ），∑φ（ζ））分别为特征空间中2类样本的均值与协方差矩阵。针对式（14），求解所获取的分类器边界即可直接转换为待估计的回归表面。

由文献［13］的结论，可以证明存在一个在高维特征空间中能以最大的概率正确分开2类的最优超平面 H（w，w0）=｛φ（g）｜wTφ（g）=w0｝，w，φ（g）∈RN，其中，g=［，x1，x2，…，xn］T，w0∈R。

将预测回归模型表面看作分类超平面H（w，w0），进一步考虑将核映射 Φ（·）＝k（·，x）作为特征空间的非线性基函数，此时有 w，φ（g）∈Rl+1，φ（g）=（，Φ1（x），Φ2（x），…，Φl（x））T，即每个 n 维输入向量被映射为具有l个特征的新的输入向量。因此，应用KMPMC，对于给定的输入x，为了预测其输出，有如下表示：wTφ（g）=w0。将 wTφ（g）=w0展开为：

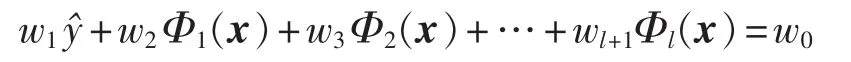
因此有：

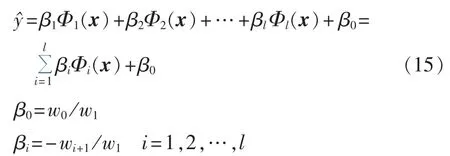
显然，由式（15）的推导看出，求解KMPMC的参数w、w0即可获取式（11）所示的KMPMR模型。

为获取参数w、w0的解，在KMPMC框架下，需考虑如下凸优化问题的解：

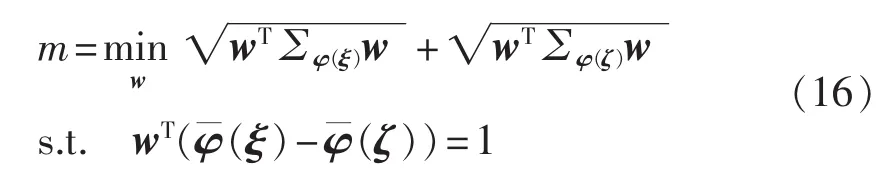
超平面的偏移量w0可由任意w唯一确定，即：

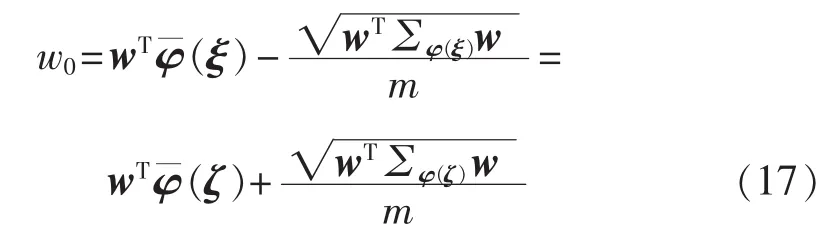
由式（17）得到 m，根据文献［12］的结论可知，分类正确的概率边界α为：

另一方面，由式（13）可知，对于由KMPMR回归模型构成的特定二分类问题，存在：

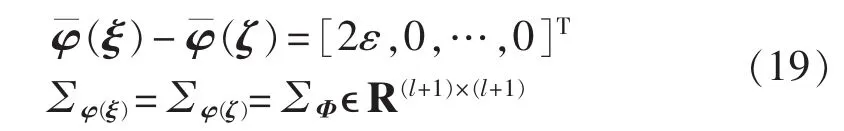
式（16）的优化问题等价于：

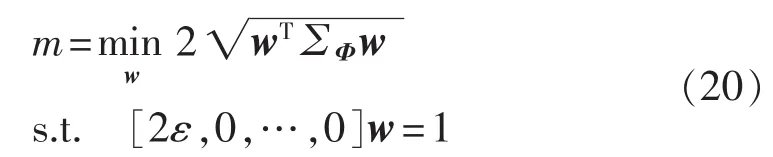
为求解方便，将式（20）等价于：

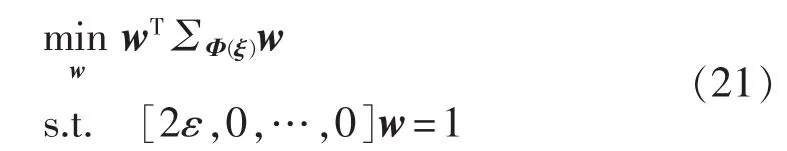
其中，∑Φ即为式（12）中协方差矩阵，为符号便利起见，可简记 zij=k（xi，xj），zi=Φi（x）=k（·，xi），则∑Φ具体可表示为：

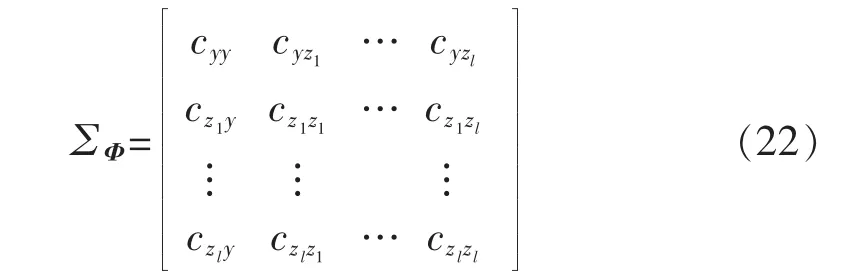
其相应元素的无偏估计为：

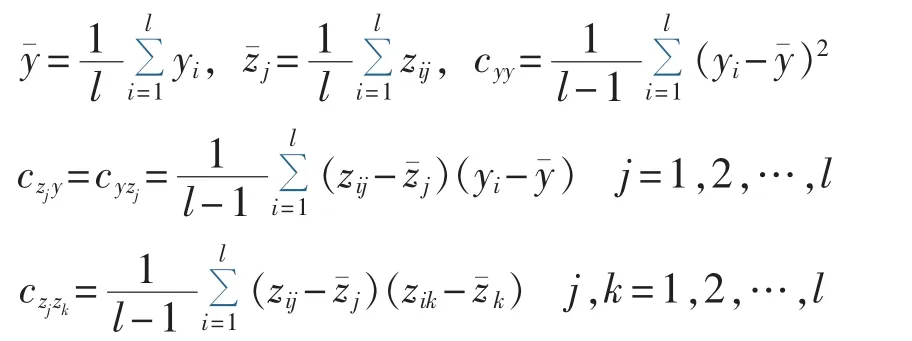
为求解式（21），可将其转化为无约束优化问题，首先构造拉格朗日函数如下：

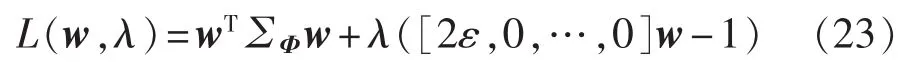
分别对w和λ求导得到：

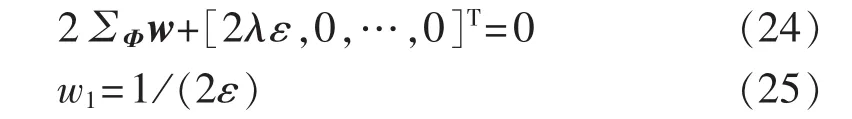
由式（24）可知，该式包含l+2个方程以及l+2个未知量：w1、w2、…、wl＋1与 λ。

然后，令拉格朗日系数自由变量λ为：

其中，（∑Φw）1表示向量∑Φw的第一个元素。将式（26）、（22）代入式（24），可约简矩阵∑Φ的第一行，因此，有：

利用，对式（27）进行变换，显然可得：

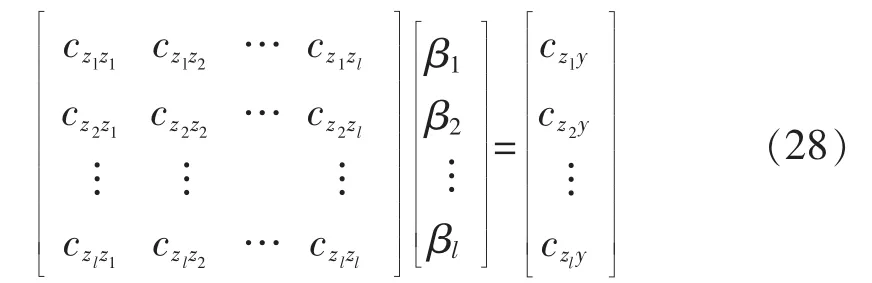
因此，实质上KMPMR模型的求解最终转换为核空间下由式（28）所示的阶次为l×l的线性方程问题求解。为避免由于矩阵的奇异性所引起解的不稳定性的缺点，定义 β=［β1，β2，…，βl］T，考虑使用奇异值分解算法求取式（28）中β的最小二乘解。

令，矩阵A的奇异值为非负矩阵 AAT的特征值的平方根，。矩阵A可以分解为：

其中，L 和 M 为正交矩阵；A1＝diag（σ1，…，σl）为对角矩阵。为保证解的稳定性，求解β时，可令阈值为χeps，满足即可。

另外，为求取 β0，利用式（17），并考虑及式（19），可得：

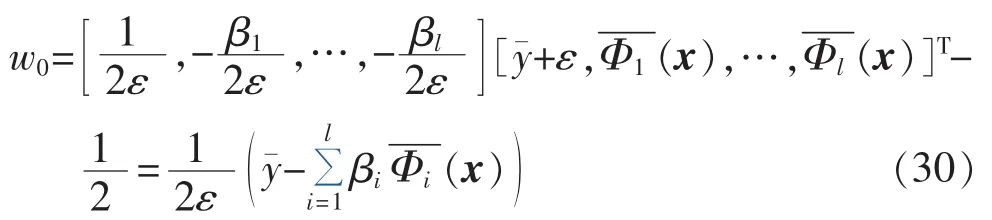
则结合式（24）有：

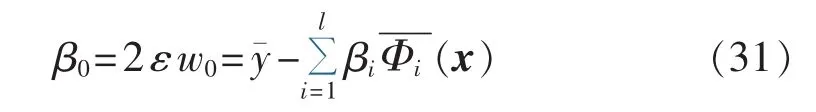
其中，。由此可见，KMPMR 方法的算法复杂度为 O（l2）。

最后，为了求取KMPMR的预测输出位于含噪声的真实输出y±ε（ε＞0）管道内的最小概率边界可以先求取分类概率边界 α，根据式（18），并结合式（20）、（25）以及利用可以推出：

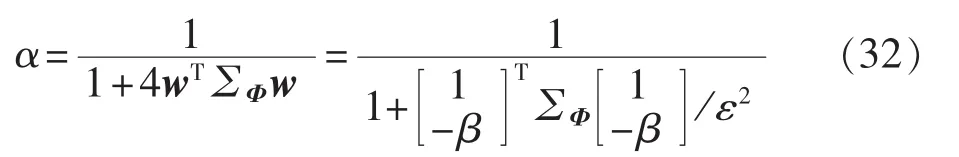
进一步，由式（13）可知，若 KMPMR的预测输出位于真实值±ε管道的内侧，则无样本被错分，当存在一个样本被误分（misclassified）时，则其预测输出位于真实值±ε管道的外侧。由于α即为样本被正确分类的下界，则被错误分类的上界为1-α，因此可得：

其中，“∨”表示“并”。所以有：

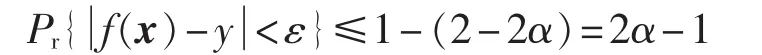
结合概率的定义，最小概率边界应满足：

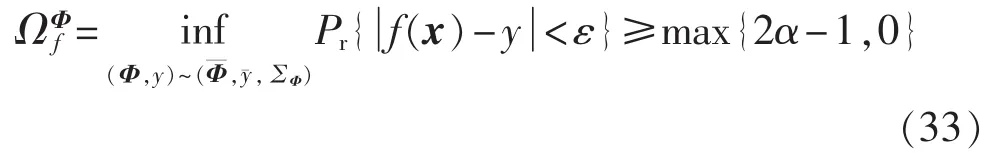
1.3 KPCA-KMPMR方法

将KPCA作为预处理过程，与KMPMR结合，可形成多层KMPMR，即有：

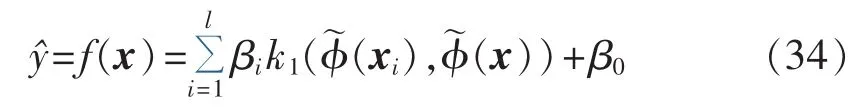
其中，主元（x）由式（9）定义。具体应用时，可考虑选择线性的核函数 k1，即 k1（x，x）=xxT。这样，在由非线性主元张成的d维子空间中，可以执行线性KMPMR模型的计算。

概言之，KPCA-KMPMR方法的实现步骤如下。

a.归一化样本数据。给定训练样本集xi∈Rn，yi∈R，归一化为均值为 0、方差为 1 的数据。

b.选择式（5）的RBF核函数形式及核参数，通过式（6）—（9）的计算，实现KPCA的特征提取，选取前 d（d≤l）个主元（x）。

c.选取不同的 ε 及线性的核 k1（x，x），并计算式（22）所示的协方差矩阵。

d.选取适宜的阈值 χeps，由式（28）利用奇异值分解算法计算 βi、β0。

e.由计算出的 β0、βi，根据式（11）计算模型的输出，再根据式（32）、（33）计算模型的最小概率边界

结合KPCA-KMPMR的算法描述可知，其算法复杂度为O（（1+d）l2）。具体预测程序流程图见图1。

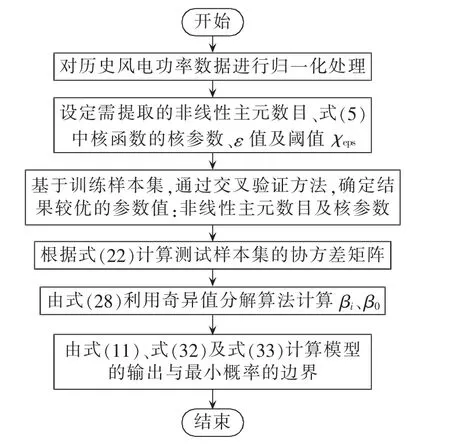
图1 基于KPCA-KMPMR方法的预测程序流程图Fig.1 Flowchart of forecasting method based on KPCA-KMPMR

2 短期风电功率预测实例

将KPCA-MPMR方法应用于不同地区的短期风电功率预测实例中。本文按照时间序列建模的方式，仅考虑历史的风电功率值，可建立形如式（34）的多层KMPMR预测模型，即：

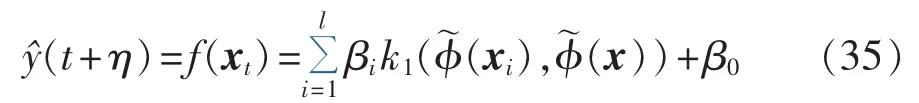
其中，t=M，M+1，…，l；η 为预测步长；xt为由历史风电功率值（yt-1，yt-2，…，yt-M）构成的向量；M 为嵌入维数；（xi）为由 KPCA 方法提取的非线性主元；f（·）由KMPMR方法构建。

具体应用实例中，KPCA-KMPMR方法的KPCA预处理时，选取形如式（5）的高斯核函数，其KMPMR方法则选取线性核函数k1。对比的单一KMPMR、SVM方法中，均选取形如式（5）的高斯核函数。

评价指标采用平均绝对百分比误差MAPE（Mean Absolute Percentage Error）、正则化均方误差NMSE（Normalized Mean Square Error）以及具有 ε精度的测试数据百分比MPTD（Measured Percentage of Test Data within ε），即：

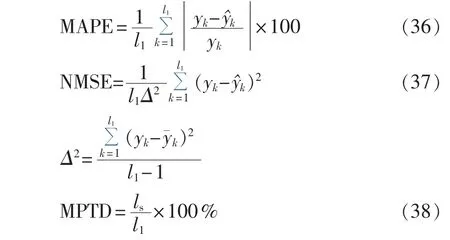
其中，yk为待预测时段第k点实际功率值；k为相应实际功率平均值；k为模型预测值；l1为预测样本点数；ls为落在y±ε管道内的样本数目。可见，MAPE、NMSE越小，MPTD越大，表明预测模型精度越高。

需要说明的是，ε任意取值（ε＞0）时，就本文方法的实现而言，其预测精度与ε无关，但MPTD与的取值会随之变化，即在一定范围内，随着ε的增大，MPTD 与均会增大。

2.1 风电功率单步预测实例

实验采用加拿大亚伯达省风电场的实测风电功率数据［18］，亚伯达省在加拿大具有最高的风电装机容量，该省的风电装机容量在逐年增加，2011年已达到800 MW左右。取亚伯达省的某一风电场在2010年12月1日到26日之间的实测风电功率数据，原始数据集的采样间隔为10 min。为构建提前0.5 h的直接预测模型，取η=1，将原始数据集的连续3个样本进行平均即可，即采样间隔为30 min。取前1000组数据作为训练，其余200组数据作为测试，预测模型的嵌入维M取48。

实验中，可通过交叉验证方法选取一组参数以获取较优的实验结果。在KPCA-KMPMR方法中，选取KPCA的高斯核函数超参数δ=7，选取的非线性主元数目为d=35，KMPMR算法实现中，χeps取为10-10，可获得较优的实验结果。

为了衡量KPCA-KMPMR方法的预测效果，在相同条件下，还将该方法与单一的KMPMR方法、SVM方法进行对比，不同方法的预测结果评价由表1列出。其中，单一的KMPMR、SVM方法中，超参数δ=7。

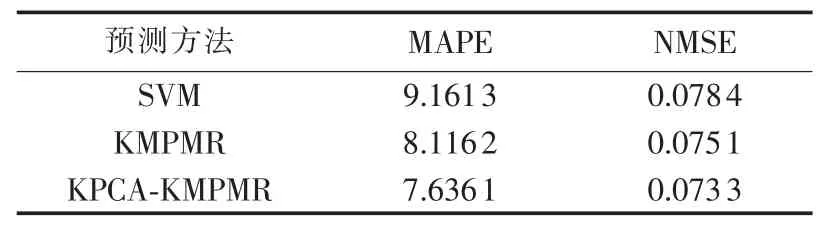
表1 KPCA-KMPMR与其他方法的预测结果对比Table 1 Comparison of forecasting results between KPCA-KMPMR and other methods

由表1可见，KPCA-KMPMR方法的MAPE值、NMSE值均最低，显示出较好的预测效果。与单一的KMPMR、SVM方法相比，经KPCA进行非线性特征提取后，KPCA-KMPMR方法的预测精度有所提高。待预测时段的实际风电功率值与本文方法的预测结果比较由图2给出，由图2看出，本文方法的预测性能较好，它能较准确地预测实际风电功率。待预测时段部分时段的不同预测方法提前0.5 h预测的各点绝对误差由图3给出，可见本文方法的预测误差波动较小，预测效果较为满意。为进一步度量预测误差概率分布情况，图4给出了ε=50时，在待预测时段本文方法的预测模型输出位于真实值±ε管道内外的分布情况。由图4可见，本文预测模型的输出绝大多数位于管道内侧，且预测值的变化趋势大致与真实值接近。同时，考虑式（32）、式（33）及式（38），可计算出：MPTD=79.50%，=32.68%，满足 MPTD＞，这进一步表明了本文概率预测方法的有效性。

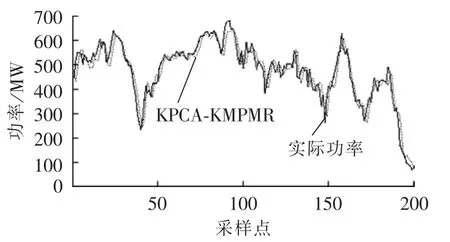
图2 基于KPCA-KMPMR的提前0.5 h的风电功率预测Fig.2 0.5 h-ahead wind power forecasting based on KPCA-KMPMR

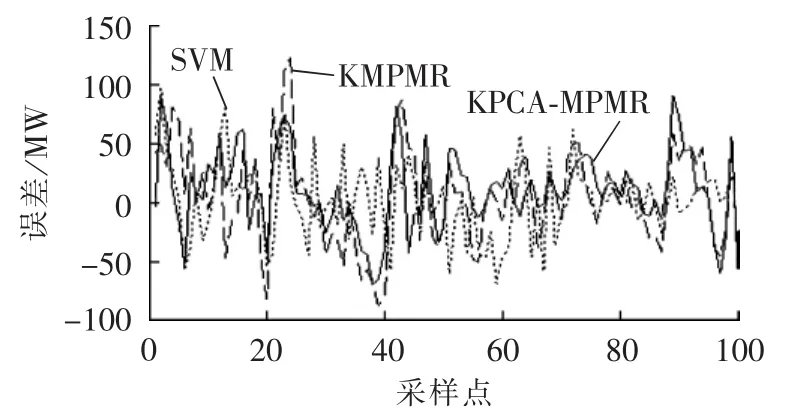
图3 不同方法提前0.5 h预测的绝对误差比较Fig.3 Comparison of absolute error among different methods for 0.5 h-ahead forecasting

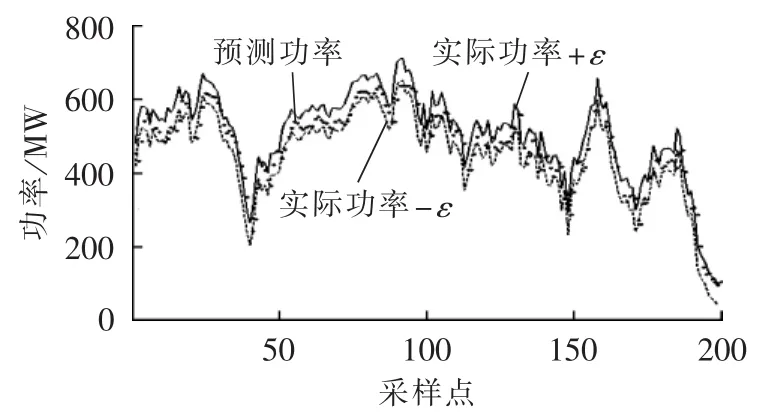
图4 基于KPCA-KMPMR的提前0.5 h的概率预测分布图Fig.4 Distribution of 0.5 h-ahead probabilistic forecasting based on KPCA-KMPMR

2.2 NREL实验室的风电功率多步预测实例

本实验选取美国国家可再生能源实验室（NREL）提供的 Western 数据集［19］。该数据集通过使用SCORE技术模拟各网格点距地面以上约100 m的10台风机的功率输出，同时还模拟了风电功率输出的随机性。原始数据集的时间采样间隔为10min，空间采样间隔为2 km。在位于科罗拉多州丹佛市以西10英里的风电场，选取68个网格点，即680组风机提供的风电功率实测数据平均值作为实验数据集，数据的采样间隔仍为10 min。取2006年6月1日至10日间共1440组数据，前1200组数据用于训练，剩余的240组数据用于测试，构建式（35）提前2 h的多步预测模型，即η=12，嵌入维数M=14。

实验中，通过交叉验证方法选取一组参数以获取较优的实验结果。在KPCA-KMPMR方法中，KPCA进行特征提取时，选取高斯核函数超参数δ=4，非线性主元数目为d=16，KMPMR的 χeps取为 10-9，可获得较优的实验结果。

为了衡量KPCA-KMPMR方法的预测效果，在相同条件下，还与单一的KMPMR、SVM方法进行了对比实验，不同方法的预测数值比较结果的评价由表2列出。其中，单一KMPMR、SVM方法的高斯核函数，选取其超参数δ=4。由表2可看出，与单一的KMPMR、SVM方法相比，本文方法的MAPE值、NMSE值均最低，显示出本文方法经KPCA进行非线性特征提取后，预测精度有所提高。

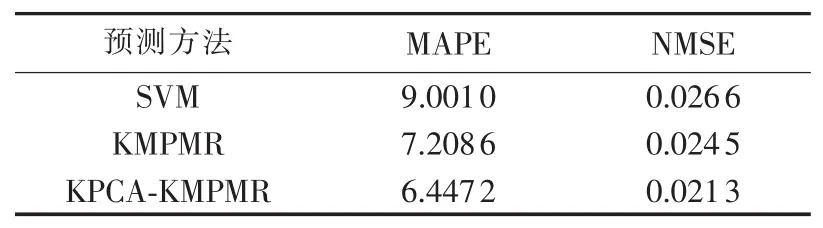
表2 KPCA-KMPMR与其他方法的预测结果对比Table 2 Comparison of forecasting results between KPCA-KMPMR and other methods

图5也给出了待预测时段的实际风电功率值与本文方法的预测结果比较。可见，KPCA-KMPMR方法的预测效果最好，它能较准确地预测实际风电功率。图6给出了待预测部分时段的不同预测方法提前2 h预测的各点绝对误差。由图6可看出，本文方法的预测误差波动较小，能取得较好的预测效果。

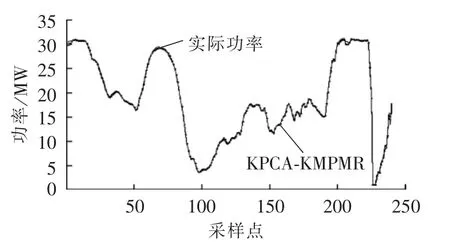
图5 基于KPCA-KMPMR的提前2 h的风电功率预测Fig.5 2 h-ahead wind power forecasting based on KPCA-KMPMR

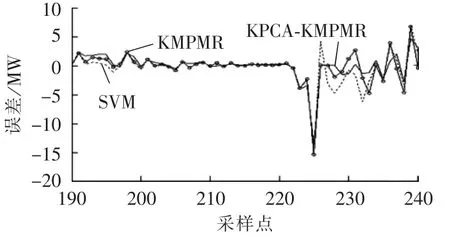
图6 不同方法提前2 h预测的绝对误差比较Fig.6 Comparison of absolute error among different methods for 2 h-ahead forecasting

为进一步分析预测误差的概率分布情况，图7给出了ε=1时，模型在待预测时段预测输出位于真实值±ε管道内外的分布情况。由图7可看出，本文预测模型的预测输出绝大多数位于管道内侧，且预测值的变化趋势大致与真实值接近。另外，由式（32）、式（33）及式（38）计算得到：MPTD=90.10%，=39.11%，满足 MPTD＞，这进一步表明利用本文方法进行短期风电功率概率预测是可行的。

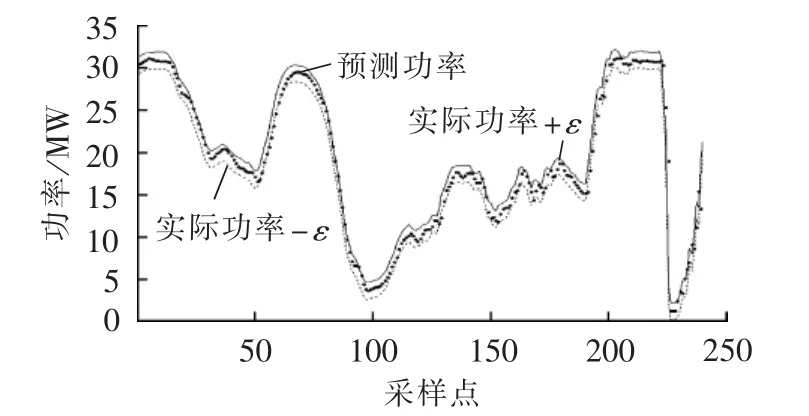
图7 基于KPCA-KMPMR的提前2 h的概率预测分布图Fig.7 Distribution of 2 h-ahead probabilistic forecasting based on KPCA-KMPMR

3 结论

针对风电功率短期预测，本文提出一种新颖的基于KPCA-KMPMR的概率预测方法。利用KPCA方法对风电功率实测数据进行非线性特征信息的提取，再应用KMPMR方法进行概率预测。通过提前0.5 h的单步预测与提前2 h的多步预测实例，对所提出方法的预测效果进行了检验，可得如下结论。

a.KPCA方法可有效地对历史风电功率时间序列数据进行预处理，提取非线性主元，具有较好的特征提取能力；KMPMR方法能在给出预测输出的同时提供预测误差分布范围。因此，结合二者优点的 KPCA-KMPMR方法保持了SVM、KMPMR原有的泛化能力，能进一步提高短期风电功率预测的精度。

b.KPCA方法的算法实现仅涉及矩阵计算，KMPMR的算法实现也相对容易，仅需求解最小二乘线性方程组问题，其阶次大小为训练数据数目。因此，本文方法的算法复杂度较低。

c.以MAPE、NMSE等指标作为评价，衡量本文方法的预测效果，与单一的KMPMR以及SVM方法相比，预测精度得到明显提升，验证了本文方法的有效性。

d.本文的模型适用于解决短期风电功率概率预测问题，具有很好的应用潜力。进一步的研究内容是考虑核独立成分分析（KICA）等其他独立成分特征提取与KMPMR相结合的预测方法。

［1］WANG X C，GUO P，HUANG X B.A review of wind power forecasting model［J］.Energy Procedia，2011，12（39）：770-778.

［2］JUNG J，BROADWATER R P.Current status and future advances forwind speed and power forecasting ［J］.Renewable and Sustainable Energy Reviews，2014，31（2）：762-777.

［3］CHOUDHARY A K，UPADHYAY K G，TRIPATHI M M.Estimation of wind power using different soft computing methods［J］.International Journal of Electrical Systems，2011，1（1）：1-7.

［4］FOLEY A M，LEAHY PG，MARVUGLIA A，etal.Current methods and advances in forecasting of wind power generation［J］.Renewable Energy，2012，37（1）：1-8.

［5］陈道君，龚庆武，金朝意，等.基于自适应扰动量子粒子群算法参数优化的支持向量回归机短期风电功率预测 ［J］.电网技术，2013，37（4）：974-980.CHEN Daojun，GONG Qingwu，JIN Zhaoyi，et al.Short-term wind power prediction based on support vector regression machine optimized by adaptive disturbance quantum-behaved particle swarm optimization［J］.Power System Technology，2013，37（4）：974-980.

［6］王丽婕，冬雷，廖晓钟，等.基于小波分析的风电场短期发电功率预测［J］.中国电机工程学报，2009，29（28）：30-33.WANG Lijie，DONG Lei，LIAO Xiaozhong，etal.Short-term power prediction of a wind farm based on wavelet analysis［J］.Proceedings of the CSEE，2009，29（28）：30-33.

［7］范高锋，王伟胜，刘纯，等.基于人工神经网络的风电功率预测［J］.中国电机工程学报，2008，28（34）：118-123.FAN Gaofeng，WANG Weisheng，LIU Chun，et al.Wind power prediction based on artificial neural network［J］.Proceedings of the CSEE，2008，28（34）：118-123.

［8］凌武能，杭乃善，李如琦.基于云支持向量机模型的短期风电功率预测［J］.电力自动化设备，2013，33（7）：34-38.LING Wuneng，HANG Naishan，LI Ruqi.Short-term wind power forecasting based on cloud SVM model［J］.Electric Power Automation Equipment，2013，33（7）：34-38.

［9］ZENG J W，QIAO W.Short-term wind power prediction using a wavelet support vector machine ［J］.IEEE Transactions on Sustainable Energy，2012，3（2）：255-264.

［10］张露，卢继平，梅亦蕾，等.基于不同优化准则的风电功率预测［J］.电力自动化设备，2015，35（5）：139-145.ZHANG Lu，LU Jiping，MEI Yilei，et al.Wind power forecasting based on different optimization criterions［J］.Electric Power Automation Equipment，2015，35（5）：139-145.

［11］刘兴杰，谢春雨.基于贝塔分布的风电功率波动区间估计［J］.电力自动化设备，2014，34（12）：26-30.LIU Xingjie，XIE Chunyu.Wind powerfluctuation interval estimation based on beta distribution［J］.Electric Power Automation Equipment，2014，34（12）：26-30.

［12］LANCKRIET G R G，GHAOUI L E，BHATTACHARYYA C，et al.Minimax probability machine［C］∥Advances in Neural Information Processing Systems 14.Cambridge，UK：MIT Press，2002：801-807.

［13］STROHMANN T R，GRUDIC G Z.Robust minimax probability machine regression［R］.Boulder，CO，USA：Department of Computer Science CU-CS-952-03，University of Colorado，2003.

［14］KUMAR M，MITTAL M，SAMUI P.Performance assessment of Genetic Programming（GP） and Minimax Probability Machine Regression（MPMR） for prediction of seismic ultrasonic attenuation［J］.Earthquake Science，2013，26（2）：147-150.

［15］ELATTAR E E，TAHA I，SHOUSH K A.Improved short term wind powerprediction using a combined locally weighted GMDH and KPCA ［J］.International Journal of Scientific&Engineering Research，2013，4（8）：1216-1224.

［16］CHEN F，HAN C.Time series forecasting based on wavelet KPCA and support vector machine［C］∥2007 IEEE International Conference on Automation and Logistics.Ji’nan，China：IEEE，2007：1487-1491.

［17］SMOLA A，SCHÖLKOPF B.A tutorial on support vector regression［J］.Statistics and Computing，2004，14（3）：199-222.

［18］Alberta Electric System Operator （AESO）.Wind power integration［EB/OL］.［2015-04-01］.http：∥www.aeso.ca/gridoperations/13902.html.

［19］POTTER C，LEW D，MCCAA J，et al.Creating the dataset for the western wind and solar integration study （USA）［J］.Wind Engineering，2008，32（4）：325-338.