基于MCKD-EMD的风电机组轴承早期故障诊断方法
2017-05-24赵洪山
赵洪山,李 浪
(华北电力大学 电气与电子工程学院,河北 保定 071003)
0 引言
风力发电作为一种清洁、高效、可再生的新型能源,近年来发展十分迅速,据中国风能协会的数据统计,截止到2015年6月底,我国风电并网总装机容量已经高达126 GW。近年来随着风力发电的大规模发展,风电机组的故障问题变得越来越突出[1-3]。轴承作为风电机组的关键部件,由于其承受复杂的载荷和处于特殊的工作环境中,极易发生故障,是导致风电机组故障停机时间最长的部件之一[4]。因此,本文对风电机组轴承的故障诊断方法进行研究,以便能够及时准确地发现轴承的早期故障,并通过采取有效措施来避免可能发生的重大事故,降低维修成本,增强机组的运行可靠性。
工程实际中,当风电机组轴承处于早期故障阶段时,由故障产生的冲击成分比较微弱,并且由环境噪声引起的干扰比较严重,使得轴承早期故障特征的提取一直面临着困难[5-6]。针对此问题已经有不少学者进行了深入研究。文献[7]提出了一种基于包络谱和循环维纳滤波的故障诊断方法,利用循环维纳滤波器对滚动轴承全寿命周期振动信号进行处理,然后通过对滤波后的信号做包络谱分析来提取微弱故障特征。文献[8]提出了一种结合小波包分解系数熵阈值和共振解调的综合算法,该方法通过提取轴承早期故障时引起的共振调制边频带,并对其进行准确研究分析,获得了较好的效果。文献[9]提出了小波相关滤波-包络分析法,利用小波相关滤波方法求得信噪比相对较高的小波系数,为了准确获取早期故障特征频率,对高频段尺度域的小波系数进行Hilbert细化包络谱分析,该方法已经在滚动轴承的早期故障诊断的应用中取得了不错的效果。
经验模态分解EMD(Empirical Mode Decomposition)是一种信号自适应分解的现代时频分析方法,通过其可得到不同尺度的波动或趋势,即本征模态函数 IMF(Intrinsic Mode Function),与其他时频分析方法相比,EMD在处理和分析非线性、非平稳信号的应用中有更好的效果。因此,EMD在故障诊断领域得到了比较广泛的应用,如文献[10]提出一种基于EMD和散度指标的风力发电机组滚动轴承故障诊断方法,取得了较好效果;文献[11]将EMD与支持向量机相结合对滚动轴承的故障类型、故障位置及故障程度进行分类;文献[12]将EMD方法应用到齿轮的故障提取和诊断中,并取得了较好的效果;文献[13]将EMD与神经网络相结合成功识别了内燃机气门间隙的故障;文献[14]采用一种改进的EMD方法,并将其成功应用到高压断路器机械故障诊断中。但在实际的强噪声环境下,IMF常常受到噪声的影响,导致微弱故障特征信号淹没在含噪声的IMF中[15]。因此研究如何有效抑制噪声对EMD的干扰,凸显出故障特征成分显得尤为重要。
最大相关峭度解卷积MCKD(Maximum Correlated Kurtosis Deconvolution)算法[16]的目的是通过解卷积运算凸出被噪声淹没的连续脉冲,提高原始信号的相关峭度值。算法的这一特性非常适用于轴承早期故障信号的降噪处理。本文针对EMD在轴承早期微弱故障特征提取的不足,提出先用MCKD对强噪声轴承信号进行降噪处理,然后对降噪后的信号进行EMD,最后选取峭度值最大的IMF作为敏感IMF并做包络谱分析,从而提取轴承的微弱故障特征。仿真和试验分析结果表明该方法能够有效应用于轴承早期故障诊断。
1 基本理论
1.1 EMD方法
EMD方法[17]是由美国国家宇航局的Huang博士于1998年首次提出的,其基本思想是所有信号均可分解为多个基本模态,各基本模态表示不同的固有简单振动,既可以是线性的,也可以是非线性的,并且各基本模态包含的极值点和零交叉点个数相同,在任意的2个相邻零交叉点之间仅有1个极值点,各模态相互独立、并无重叠。
EMD算法的流程见图1,以任意信号x(t)为例,分解步骤如下所示。
a.提取信号x(t)所有的局部极大值与极小值点。
b.利用三次样条插值法分别连接局部极大值与局部极小值点,构造信号x(t)的上包络线u(t)与下包络线 v(t)。
c.计算上、下包络线的平均值。
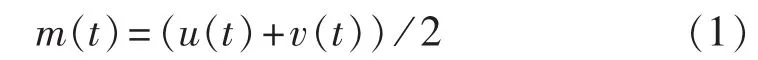
d.将信号 x(t) 减去 m(t) 得到 h(t)。
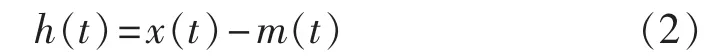
e.如果h(t) 满足 IMF 条件,则h(t)为信号x(t)IMF 的一阶分量 c1(t);如果 h(t) 不满足 IMF 条件,将h(t)作为新的信号,重复步骤a至步骤d,直到其满足IMF条件为止。
f.将 c1(t) 从原始信号 x(t) 中分离出来,得到残余项 r(t),判断残余项 r(t)能否继续分解,若能则将r(t)作为新的信号重复以上步骤,若不能则循环结束。
至此,信号的EMD结束,最终得到信号x(t)的若干个IMF分量和一个残余量r(t),即:
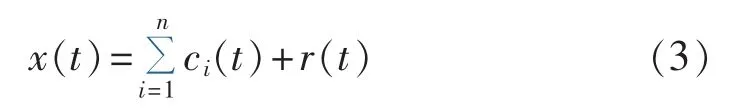
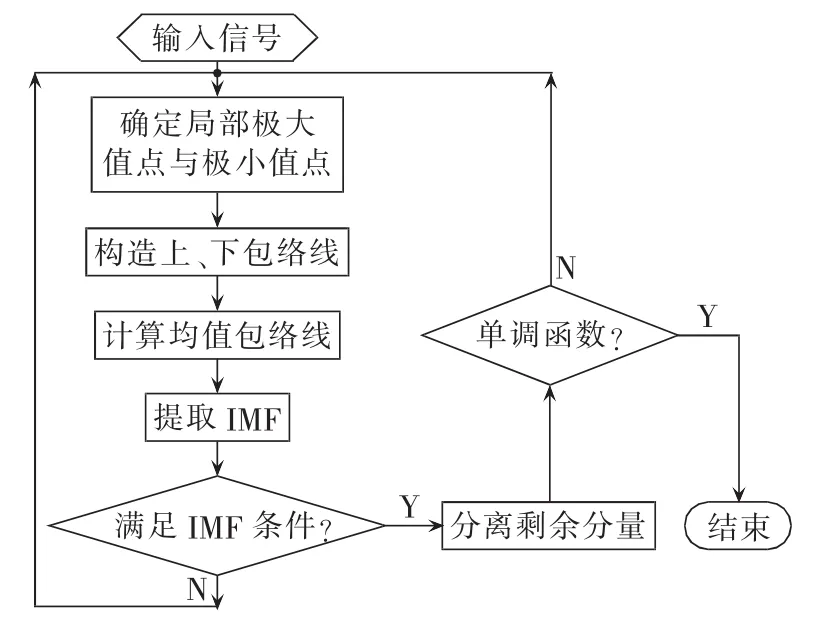
图1 经验模态分解算法流程图Fig.1 Flowchart of EMD algorithm
1.2 MCKD算法
MCKD 算法中信号 xn(n=1,2,…,N)的相关峭度定义公式如式(4)所示。
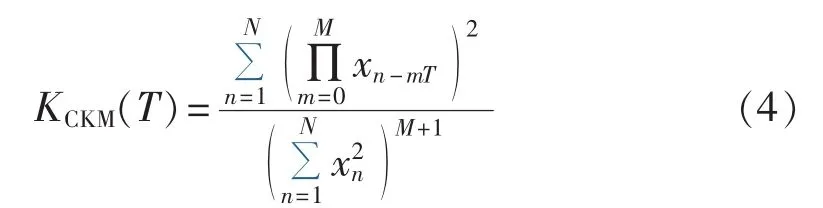
其中,T为冲击信号的周期;M为位移数。相关峭度充分考虑了冲击成分的连续性,是衡量信号中故障脉冲序列所占比重的关键指标。
在轴承出现故障时,传感器采集到的振动信号 为[18]:

为了便于分析,在此先不考虑噪声en的影响。假定输入xn为轴承故障产生的冲击信号,hn为xn经过周围环境及传输过程中受到的干扰,yn为传感器采集到的振动信号。冲击序列xn经hn作用后,信号yn中反映故障特征的脉冲序列被掩盖,从而使相关峭度变小。MCKD算法的本质是寻找一个有限长单位冲激响应 FIR(Finite Impulse Response)滤波器 wl,由输出序列yn恢复输入序列xn,即:

MCKD算法的目的是利用解卷积将被掩盖的故障脉冲信号凸显出来,因此该算法的目标函数为最大化相关峭度,即:
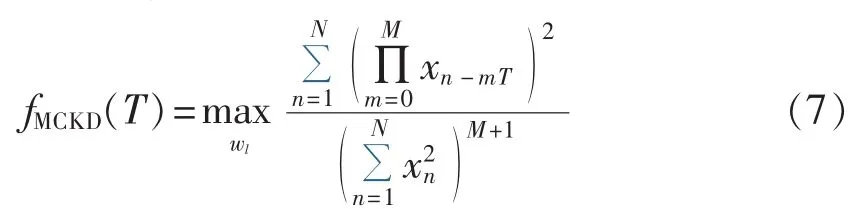
其中,l=1,2,…,L。
寻找最优滤波器 wl,使 KCKM(T)最大,即:
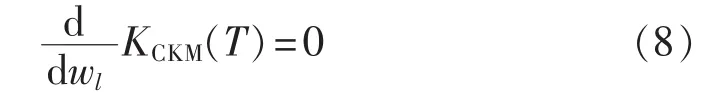
通过下式计算可得到滤波器的各项系数:

综上所述,将MCKD算法步骤归纳如下:
a.初始化解卷积周期T、位移数M及滤波器长度L等参数;
b.计算信号yn的与YmT;
c.计算滤波后的输出信号xn;
d.根据xn计算Am与B;
e.更新滤波器的系数wl;
f.如果滤波前与滤波后信号的相关峭度差值ΔKCKM(T)小于阈值,结束迭代,否则重复步骤c—e。
2 基于MCKD-EMD轴承早期故障诊断方法
当风电机组轴承发生早期故障时,与故障有关的冲击特征非常微弱。为了有效地提取早期故障特征,本文提出了基于MCKD结合EMD的轴承早期故障诊断方法,即MCKD-EMD方法,其算法流程见图2,具体的步骤如下。
a.采集振动信号x(t)。确定轴承测点,设置传感器采样率为fs,实时采集轴承振动数据。
b.利用MCKD对x(t)降噪。初始化MCKD算法的各项参数,并利用MCKD算法对传感器现场采集的振动信号x(t)进行降噪,凸显出冲击成分。
c.对降噪信号进行EMD。利用EMD方法对降噪后的信号做进一步处理,得到一组IMF分量。
d.提取敏感IMF。在EMD分解得到的一组IMF分量中,峭度值最大的IMF所包含的冲击信号最为丰富,其反映轴承故障的特征信息也更为集中。因此,选取峭度值最大的IMF作为敏感IMF。
e.Hilbert包络谱分析。利用Hilbert变换对敏感IMF进行包络解调,提取出包络信号并利用傅里叶变换做频谱分析,从而获得敏感IMF的包络谱图。
f.故障诊断。将包络谱中幅值凸出的频率成分与风电机组轴承的故障特征频率理论值进行对比,实现故障最终判别。
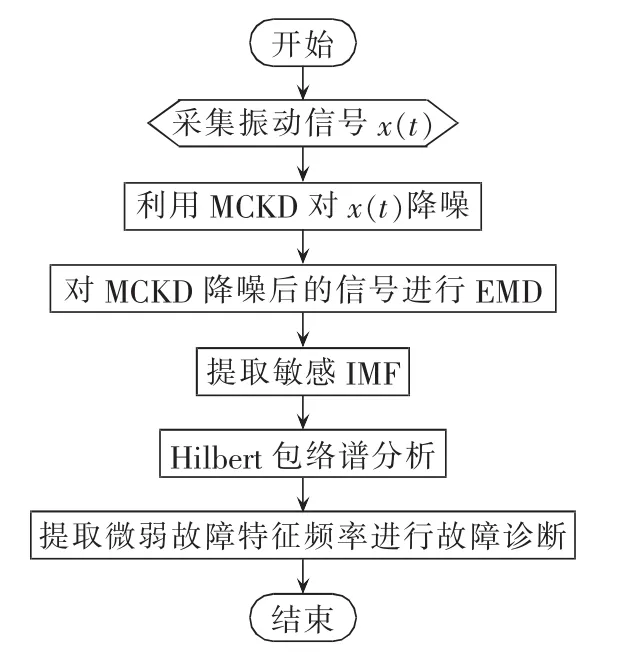
图2 轴承早期故障诊断流程图Fig.2 Flowchart of incipient bearing fault diagnosis
3 仿真分析
为了验证本文方法的有效性,利用Randall的滚动轴承模型[19]对轴承内圈点蚀故障进行模拟。该轴承模型综合考虑了轴承结构、滚珠滑动干扰、调幅、公差、磨损损伤等多个因素的影响,其数学模型如式(10)所示。
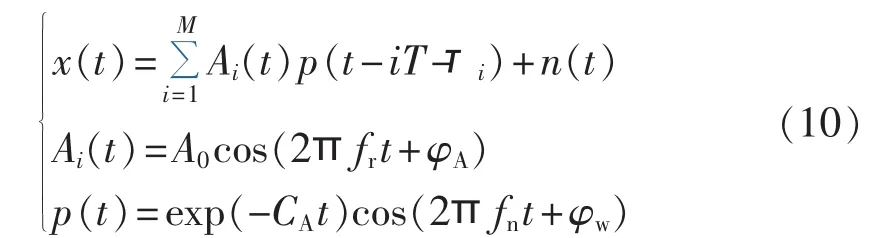
其中,Ai(t)为第i次冲击调节幅值的函数因子;T为冲击产生的周期;转频 fr为 12 Hz;p(t) 为故障产生的某次冲击振荡;Ti为第i次冲击对于平均周期T的微小波动,假定其服从均值为0、标准差为转频0.5%的正态分布;滚动轴承的系统共振频率fn为4000Hz;轴承内圈故障特征频率fi=1/T=57 Hz;A0为常数2;衰减系数CA为800,大小的选取与轴承型号有关;加入噪声n(t)后信号的信噪比为-12 dB,采样频率fs为 23 kHz。
根据上述模型生成轴承内圈故障的仿真信号,其中未加噪声的仿真信号波形如图3(a)所示,加强噪声的仿真信号波形如图3(b)所示,对比图3(a)、(b)可明显看出,当背景噪声较强时,仿真信号中反映故障信息的冲击脉冲几乎完全被掩盖。对加入强噪声后的仿真信号进行Hilbert变换,得到其包络谱如图3(c)所示,可见包络谱中并无幅值凸出的频率成分,无法对轴承内圈故障特征进行有效提取。
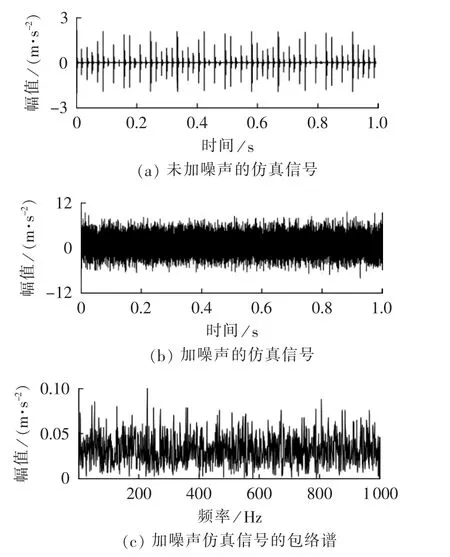
图3 轴承内圈故障仿真Fig.3 Simulative fault signals of inner-ring fault
利用EMD方法对图3(b)所示信号进行分解得到IMF,图4为IMF前8阶分量c1—c8的时域波形。分别计算IMF前8阶分量c1—c8的峭度值见表1,从表1所示的结果中可发现第4阶IMF分量c4的峭度值K最大。选取c4作为敏感IMF并进一步地对其做包络谱分析,结果见图5,在图5(b)所示的包络谱中很难分辨出轴承内圈模拟故障的特征频率为57 Hz。
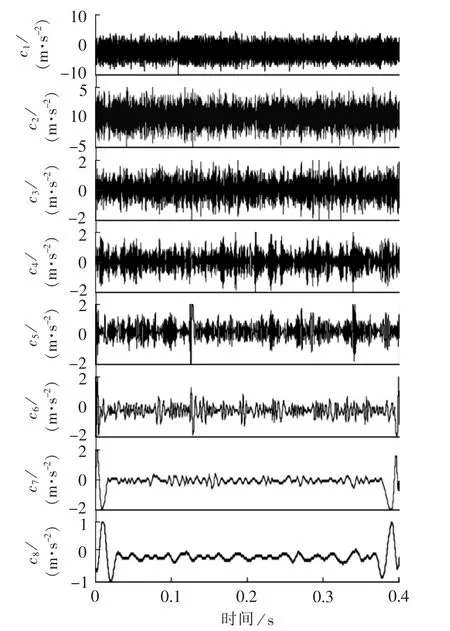
图4 对仿真故障信号进行直接EMD的结果c1—c8Fig.4 c1-c8,results of EMD for simulative fault signals
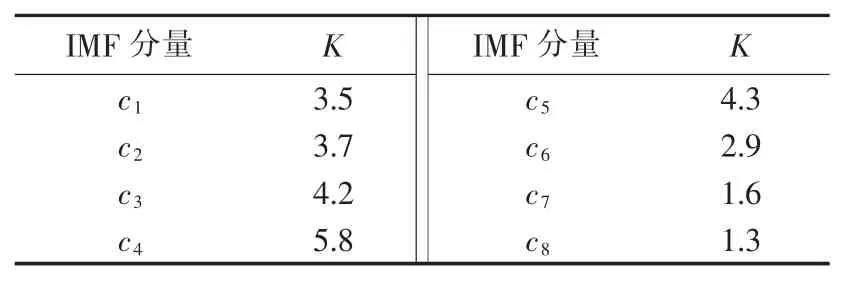
表1 直接EMD分解的IMF峭度值Table 1 Kurtosis of IMFs by EMD
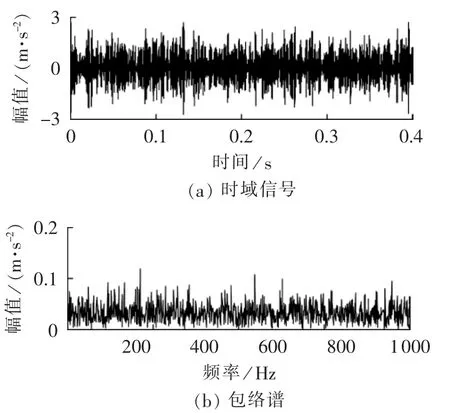
图5 c4时域波形及包络谱Fig.5 Time-domain waveform and envelope spectrum of c4
为了消除噪声的影响,用MCKD算法对图3(b)所示仿真信号降噪处理,并对降噪后的信号进行EMD得到一组本征模态函数,其前8阶分量c1—c8的时域波形如图6所示。分别计算IMF前8阶分量的峭度值,结果见表2,可发现第2阶IMF分量c2的峭度值最大。因此,选取c2作为敏感IMF并计算其包络谱,结果如图7所示,其中图7(a)显示的是c2的时域信号波形,图7(b)为其包络谱,可以看出在包络谱中轴承内圈故障频率fi及其2倍频、3倍频处的幅值明显凸出,故障特征被很好地提取。
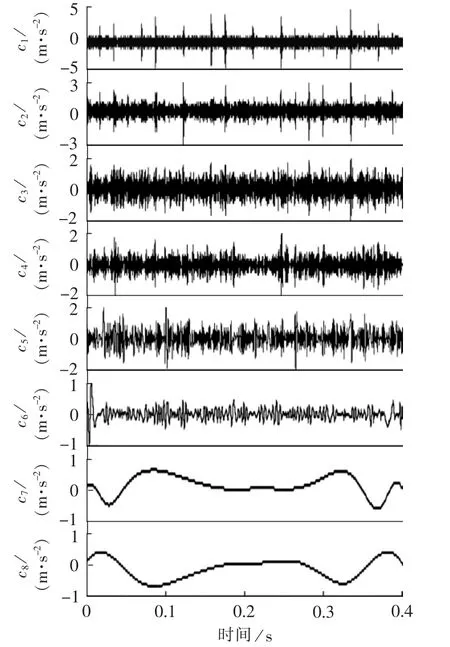
图6 仿真故障信号经MCKD处理后的EMD结果,c1—c8Fig.6 c1-c8,results of MCKD-EMD for simulative fault signals
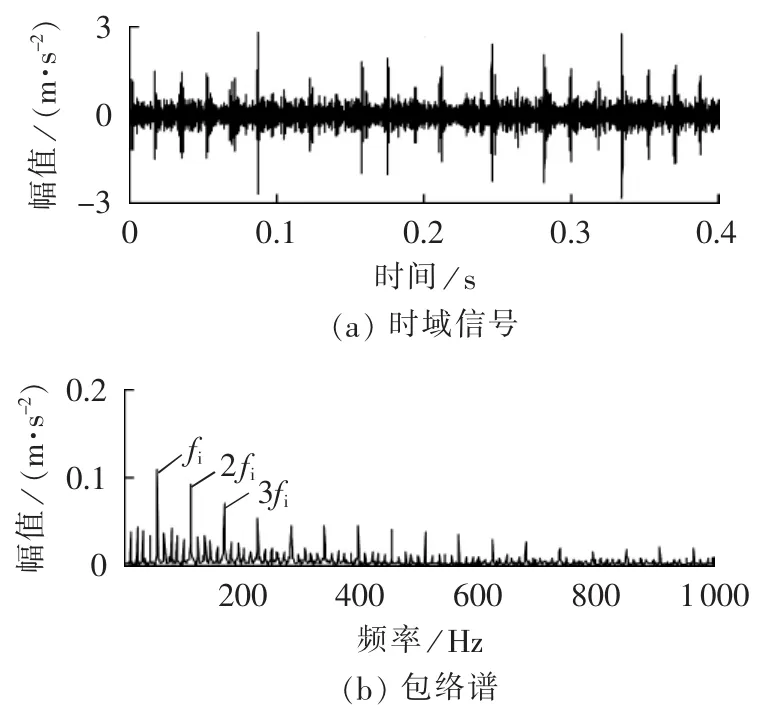
图7 c2时域波形及包络谱Fig.7 Time-domain waveform and envelope spectrum of c2
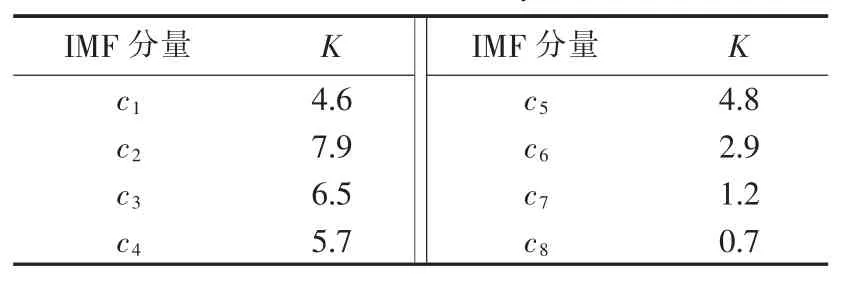
表2 MCKD降噪后由EMD得到的IMF峭度值Table 2 Kurtosis of IMFs by MCKD-EMD
仿真分析结果表明,当信号中反映故障信息的冲击信号淹没在强背景噪声中时,如果直接对其进行EMD并进行包络解调,无法有效地提取出故障特征频率,而利用本文提出的MCKD-EMD方法对原信号进行处理后,从包络谱中可准确地提取故障特征频率,实现轴承故障的有效诊断。
4 试验分析
本文在风力发电机组试验台上进行了轴承损伤类故障试验,并通过自行研发的高精度信号采集模块DR-4001测取轴承故障的振动数据。试验台主要由叶片、主轴承、齿轮箱以及发电机组成,结构示意图如图8所示。主轴承为滚动轴承,主要承受径向载荷,同时也可承受由于风对风轮作用产生的部分轴向载荷[20-21]。试验过程中主轴的转速恒定不变,传感器采样率fs为10 kHz,采样点数为5000。考虑到滚动轴承的局部损伤可能发生在外圈和内圈上,分别在轴承的内、外圈上切割沟槽来模拟轴承的局部损伤,如图9所示。
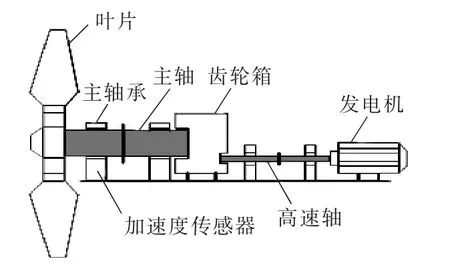
图8 试验台示意图Fig.8 Schematic diagram of test platform

图9 轴承局部损伤图Fig.9 Partial damages of bearing
轴承内、外圈故障的特征频率计算公式分别如式(11)、(12)所示:
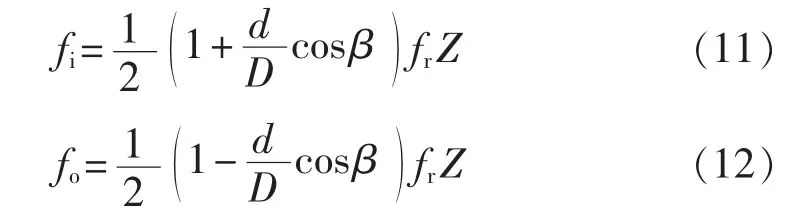
其中,fi为轴承内圈故障特征频率;fo为轴承外圈故障特征频率;fr为轴的转频;D为轴承节径;d为滚动体直径;β为轴承的接触角;Z为滚动体数量。当主轴的转速为 280 r/min 时,根据式(11)、(12)可计算得到轴承内圈故障频率fi为155.8 Hz,外圈故障频率fo为 105.4 Hz。
4.1 轴承内圈故障分析
试验采集的风电机组主轴承内圈故障振动信号时域波形如图10(a)所示,在图中隐约可见少量冲击成分,但并无任何规律。对内圈故障信号进行傅里叶变换,得到其幅值谱如图10(b)所示,可以看出信号的能量基本均匀分布在宽频范围内。图10(c)为内圈故障信号的包络谱,在图中没有发现幅值凸出的频率成分,由此可见传统的傅里叶变换和包络谱分析均无法有效地提取该故障信号的特征。

图10 风电机组轴承内圈故障信号Fig.10 Inner-ring fault signals of wind-power unit
对内圈故障信号进行EMD并选取峭度值最大的c1作为敏感IMF,其时域波形如图11(a)所示。图11(b)是敏感IMF的包络谱分析结果,可见仍无法提取风电机组轴承内圈故障的特征频率。
利用MCKD算法对图10(a)所示的内圈故障信号进行降噪处理,并进一步对降噪信号进行EMD。选取峭度值最大的c3作为敏感IMF,其时域波形如图12(a)所示,可发现其中反映故障信息的冲击脉冲信号明显凸出。图12(b)是敏感IMF的包络分析结果,可以清楚地看到包络谱中主要频率成分为内圈故障特征频率(156 Hz)及其 2 倍频(312 Hz),并且几乎没有其他幅值明显的频率成分,表明风电机组轴承内圈存在局部损伤。
4.2 轴承外圈故障分析
图13中,从上到下依次为风电机组轴承外圈故障振动信号的时域波形、幅值谱及其包络谱图。图14为直接对外圈故障信号进行EMD得到的敏感IMF时域波形及其包络谱。利用本文所提MCKD-EMD方法对外圈故障信号进行分析得到敏感IMF,其时域波形及包络谱分别如图15(a)、(b)所示。与内圈故障试验结果类似,仅从利用MCKD-EMD方法分析得到的包络谱中才可以准确得到外圈故障特征频率(105 Hz)及其 2 倍频(209 Hz),根据分析结果可判断风电机组轴承外圈存在局部损伤。通过分析内、外圈故障试验结果可发现,本文提出的MCKD-EMD方法能很好地诊断出轴承早期故障。
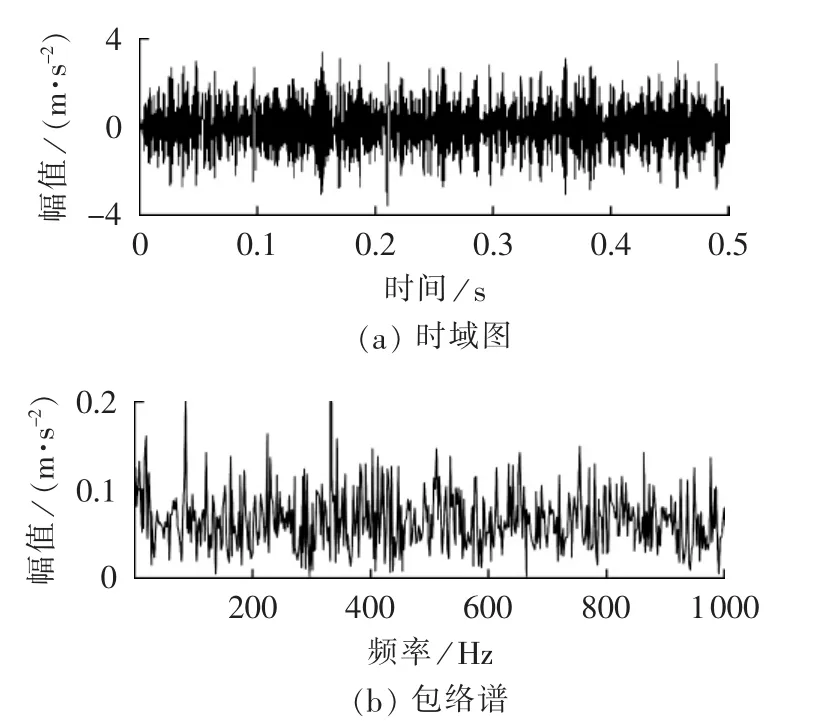
图11 轴承内圈故障EMD结果c1Fig.11 c1,result of EMD for inner-ring fault
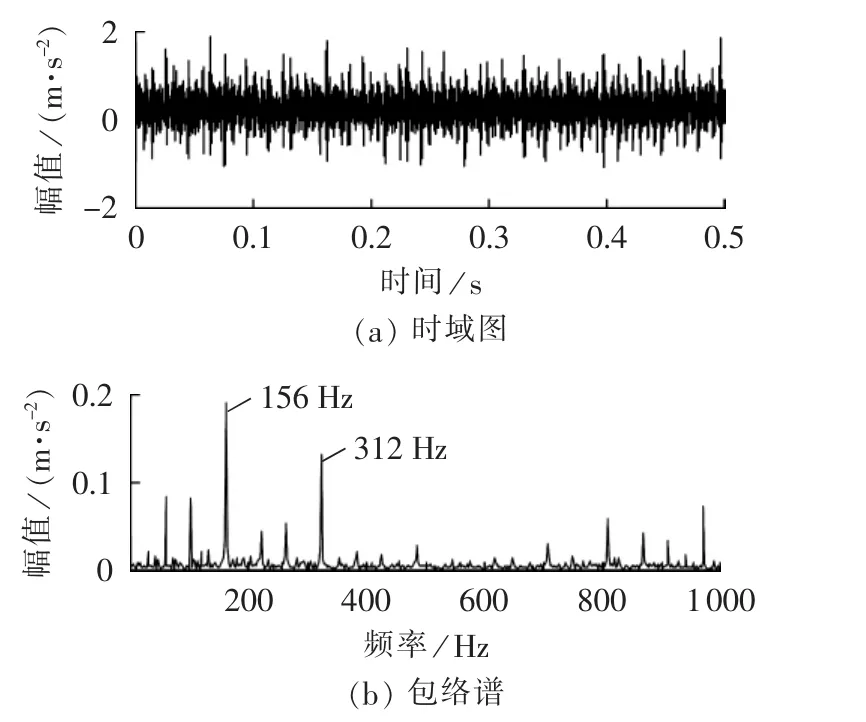
图12 轴承内圈故障MCKD降噪后的EMD结果c3Fig.12 c3,result of MCKD-EMD for inner-ring fault
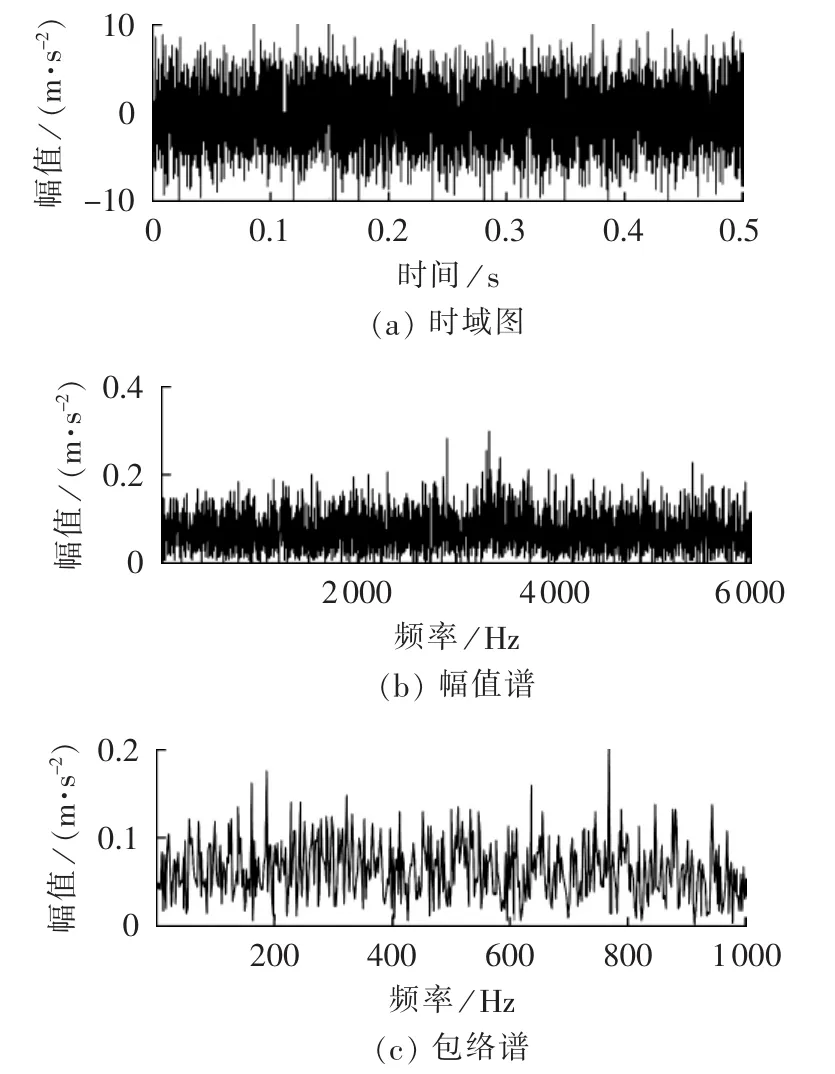
图13 风电机组轴承外圈故障信号Fig.13 Outer-ring fault signals of wind-power unit
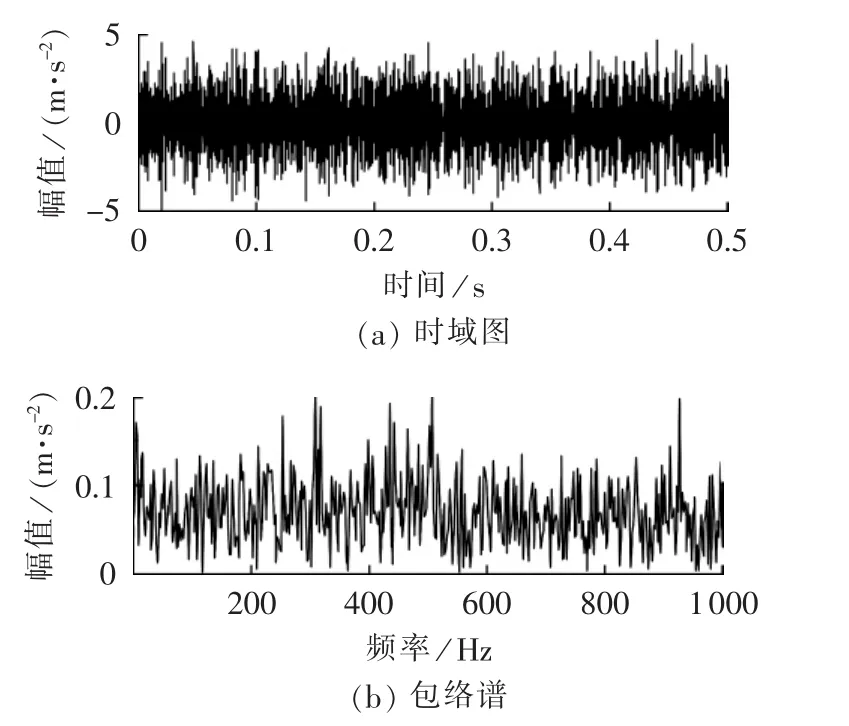
图14 轴承外圈故障EMD结果c3Fig.14 c3,result of EMD for outer-ring fault
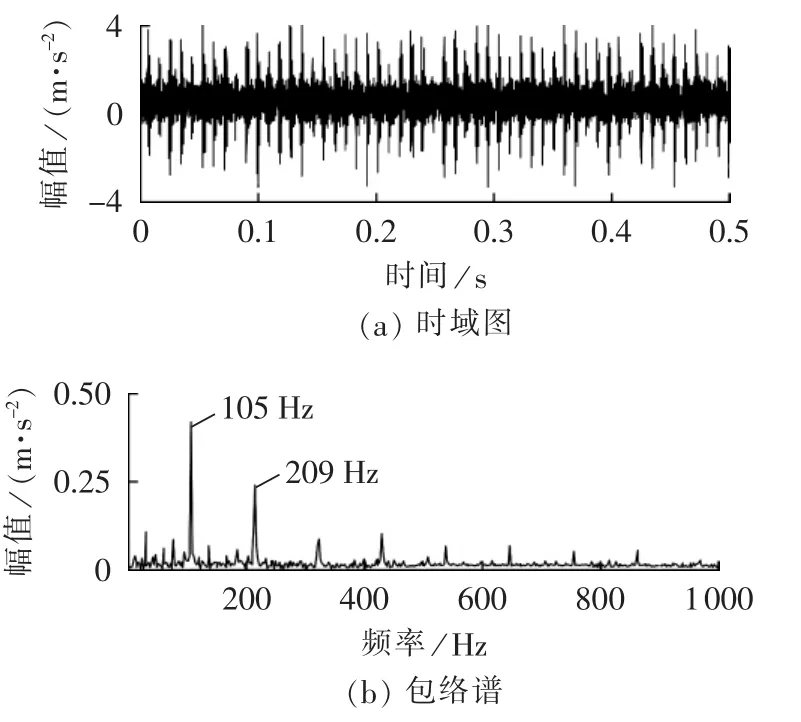
图15 轴承外圈故障MCKD降噪后的EMD结果c2Fig.15 c2,result of MCKD-EMD for outer-ring fault
5 结语
针对EMD在风电机组轴承早期故障特征提取方面的不足,本文提出了基于MCKD与EMD相结合的故障诊断方法,利用MCKD算法的滤波作用减弱了噪声对EMD的影响,以便更有效地提取轴承的故障特征。通过分析仿真和试验结果,证明MCKDEMD方法可以有效地消除轴承故障信号中混有的强背景噪声,准确地诊断轴承的早期故障。总体而言,MCKD-EMD方法为风电机组故障诊断提供了一种新的思路,对风电机组状态监测与故障诊断技术的开发,具有一定的参考价值。
[1]赵洪山,郭伟,邵玲,等.基于子空间方法的风机齿轮箱故障预测算法[J].电力自动化设备,2015,35(3):27-32.ZHAO Hongshan,GUO Wei,SHAO Ling,et al.Gearbox fault prediction algorithm based on subspace method for wind turbine[J].Electric Power Automation Equipment,2015,35(3):27-32.
[2]赵洪山,连莎莎,邵玲.基于模型的风电机组变桨距系统故障检测[J].电网技术,2015,39(2):440-444.ZHAO Hongshan,LIAN Shasha,SHAO Ling.A model-based faultdetection forvariable-pitch system ofwind turbines[J].Power System Technology,2015,39(2):440-444.
[3]安学利,蒋东翔,陈杰,等.基于ITD和LS-SVM的风力发电机组轴承故障诊断[J].电力自动化设备,2011,31(9):10-13.AN Xueli,JIANG Dongxiang,CHEN Jie,etal.Bearing fault diagnosisbased on ITD and LS-SVM forwind turbine[J].Electric Power Automation Equipment,2011,31(9):10-13.
[4]赵洪山,邵玲,连莎莎.基于最大信噪比的风电机组主轴承故障特征提取[J].可再生能源,2015,33(3):410-415.ZHAO Hongshan,SHAO Ling,LIAN Shasha.Method for extracting fault feature of wind turbine main bearing based on maximum signal to noise ratio[J].Renewable Energy Resources,2015,33(3):410-415.
[5]雷亚国,韩冬,林京,等.自适应随机共振新方法及其在故障诊断过中的应用[J].机械工程学报,2012,48(7):62-67.LEI Yaguo,HAN Dong,LIN Jing,et al.New adaptive stochastic resonance method and its application to fault diagnosis[J].Chinese Journal of Mechanical Engineering,2012,48(7):62-67.
[6]罗忠辉,薛晓宁,王筱珍,等.小波变换及经验模式分解方法在电机轴承早期故障诊断中的应用[J].中国电机工程学报,2005,25(14):125-129.LUO Zhonghui,XUE Xiaoning,WANG Xiaozhen,et al.Study on the method of incipient motor bearing fault diagnosis based on wavelet transform and EMD[J].Proceedings of the CSEE,2005,25(14):125-129.
[7]MING Y,CHEN J,DONG G.Weak fault feature extraction of rollingbearingbased on cyclicWienerfilterand envelope spectrum[J].Mechanical System and Signal Processing,2011,25(5):1773-1785.
[8]崔玲丽,康晨晖,胥永刚,等.滚动轴承早期冲击性故障特征提取的综合算法研究 [J].仪器仪表学报,2010,31(11):2422-2427.CUI Lingli,KANG Chenhui,XU Yonggang,etal.Integrated algorithm research on early impactive fault feature extraction of rolling beraring[J].Chinese Journal of Scientific Instrument,2010,31(11):2422-2427.
[9]曾庆虎,邱静,刘冠军,等.基于小波相关滤波-包络分析的早期故障特征提取方法[J].仪器仪表学报,2008,29(4):729-733.ZENG Qinghu,QIU Jing,LIU Guanjun,et al.Approach to extraction of incipient fault features based on wavelet correlation filter and envelope analysis[J].Chinese Journal of Scientific Instrument,2008,29(4):729-733.
[10]郭燕平,颜文俊,包哲静,等.基于经验模态分解和散度指标的风力发电机滚动轴承故障诊断方法[J].电力系统保护与控制,2012,40(17):83-87.GUO Yanping,YAN Wenjun,BAO Zhejing,et al.Fault diagnosis of bearing in wind turbine based on empirical mode decomposition and divergence index[J].Power System Protection and Control,2012,40(17):83-87.
[11]康守强,王玉静,杨广学,等.基于经验模态分解和超球多类支持向量机的滚动轴承故障诊断方法[J].中国电机工程学报,2011,31(14):96-102.KANG Shouqiang,WANG Yujing,YANG Guangxue,et al.Rolling bearing fault diagnosis method using empirical mode decomposition and hypersphere multiclass support vector machine[J].Proceedings of the CSEE,2011,31(14):96-102.
[12]程军圣,于德介,杨宇,等.基于EMD的齿轮故障识别研究[J].电子与信息学报,2004,26(5):825-829.CHENG Junsheng,YU Dejie,YANG Yu,etal.Researchon gear fault diagnosis based on EMD[J].Journal of Electronics and Information Technology,2004,26(5):825-829.
[13]王祝平,王为,李小昱,等.基于EMD与神经网络的内燃机气门间隙故障诊断[J].农业机械学报,2007,38(12):133-136.WANG Zhuping,WANG Wei,LI Xiaoyu,et al.Fault diagnosis of engine valve based on EMD and artificial neural network[J].Transactions ofthe Chinese Society for Agricultural Machinery,2007,38(12):133-136.
[14]黄建,胡晓光,巩玉楠.基于经验模态分解的高压断路器机械故障诊断方法[J].中国电机工程学报,2011,31(12):108-113.HUANG Jian,HU Xiaoguang,GONG Yunan.Machinery fault diagnosis of high voltage circuit breaker based on empirical mode decomposition [J].Proceedings of the CSEE,2011,31(12):108-113.
[15]王玉静,康守强,张云,等.基于集合经验模态分解敏感本征模态函数选择算法的滚动轴承状态识别方法[J].电子与信息学报,2014,36(3):595-600.WANG Yujing,KANG Shouqiang,ZHANG Yun,et al.Condition recognition method ofrolling bearing based on ensemble empirical mode decomposition sensitive intrinsic mode function selection algorithm[J].Chinese JournalofElectronics and Information Technology,2014,36(3):595-600.
[16]MCDONALD G L,ZHAO Qing,ZUO M J.Maximum correlated kurtosis deconvolution and application on gear tooth chip fault detection[J].Mechanical System and Signal Processing,2012,33(1):237-255.
[17]钟佑明,秦树人,唐宝平.一种振动信号新变换法的研究[J].振动工程学报,2002,15(2):233-237.ZHONG Youming,QIN Shuren,TANG Baoping.Study on a new transform method for vibration signal[J].Chinese Journal of Vibration Signal,2002,15(2):233-237.
[18]王宏超,陈进,董广明.基于最小熵解卷积与稀疏分解的滚动轴承微弱故障特征提取[J].机械工程学报,2013,49(1):88-94.WANG Hongchao,CHEN Jin,DONG Guangming.Fault diagnosis method for rolling bearing’s weak fault based on minimum entropydeconvolution and sparse decomposition[J].Chinese Journal of Mechanical Engineering,2013,49(1):88-94.
[19]RANDALL R B,ANTONI J,CHOBSAARD S.The relationship between spectralcorrelation and envelope analysisin the diagnostics of bearing faults and other cyclostationary machine signals[J].Mechanical Systems and Signal Processing,2001,15(5):945-962.
[20]朱云国,张兴,刘淳,等.无刷双馈风力发电机的无速度传感器矢量控制技术[J].电力自动化设备,2013,33(8):125-130.ZHU Yunguo,ZHANG Xing,LIU Chun,et al.Sensorless vector control technology for brushless doubly-fed wind power generator[J].Electric Power Automation Equipment,2013,33(8):125-130.
[21]李辉,胡姚刚,李洋,等.大功率并网风电机组状态监测与故障诊断研究综述[J].电力自动化设备,2016,36(1):6-16.LI Hui,HU Yaogang,LI Yang,et al.Overview ofcondition monitoring and fault diagnosis for grid-connected high-power wind turbine unit[J].Electric Power Automation Equipment,2016,36(1):6-16.
