考虑风电机无功调节能力的配电网有功/无功联合调度
2017-05-24黄松柏
黄松柏
(湖北理工学院 电气与电子信息工程学院,湖北 黄石 435003)
0 引言
随着全球性的能源危机及国家对减排降耗的强制规定,以风电为代表的新能源渗透率不断提高。而新能源普遍具有的间歇性和随机性,给电网的安全稳定运行带来较大的影响。
新能源的随机性会直接导致节点注入功率的随机性,使得网络损耗、电压稳定裕度等运行指标均具有随机性。为控制随机性对系统的影响,一般可采用新能源集群接入[1]或者针对随机场景进行预防控制[2-3]。目前在输电网中,风电主要是以集群的形式接入。而在配电网中,风电通常采用分布式接入,间歇性和随机性更加明显,因此有必要在随机场景下对配电网进行优化。
目前,大多数随机调度模型均基于期望值的目标函数[3-5],无法计及随机性所带来的运行风险。文献[6]和文献[7]分别提出基于分位数和超分位数的目标函数定义方式,可计及方案的运行风险,但这2种方法目前均只能依赖模拟法[8-9]或点估计法[2]求解,增加了计算复杂度和求解难度。因此有必要对目标函数进行改进,使得在计算复杂度可接受的条件下获得具有运行风险较小的调度方案。
传统配电网是辐射形电网,潮流沿传输线向系统末端节点流动,运行中只需将电压控制在合理的范围内就可以保证系统的安全运行。而大量分布式风电接入后,配电网成为多电源网络,潮流分布的方式变化较大,容易由于无功分布的不平衡导致电压问题。另外在配网中一般R较大(不满足R≪X),这使得配电网中有功分布也对节点电压稳定性具有一定影响。为保障配电网的安全稳定运行,文献[10]应用多场景方法对分布式风电出力进行建模,以网损和雅可比矩阵最小奇异值作为目标函数,将风电出力分为额定运行、欠额定、停机3个场景对风电接入的配电网无功进行优化,但仅设置3个出力场景会带来一定误差,而雅可比矩阵奇异值作为电压稳定指标不直观且具有较强非线性,在系统重载情况下,矩阵奇异值微小的变化就会导致电压失去稳定。文献[2]以网损为目标,电压稳定裕度为约束,通过投切电容器保障配电网的安全稳定运行。但该方法对风电机的处理较为粗糙,仅作为负的负荷纳入节点,运行中一直保持不变的功率因数,未考虑风电机的调节能力。文献[11]提出应当在配电网优化调度中考虑分布式风电机的调节作用,但对风电机的输出功率仅采用恒定上限模型,实际上会乐观估计风电机的调节能力。
目前广泛采用的双馈风电机组DFIG(Doubly-Fed Induction Generator)可通过控制输出功率的功率因数角调整输出有功/无功的大小。文献[12-13]通过功率极限曲线建立较详细的双馈电机输出功率模型,但针对分布式风电机,风速的波动性使得风电机不可能一直工作在额定功率,因此需针对随机风速,建立更完善的双馈风电机功率输出模型。
针对以上问题,本文模型同时考虑目标函数的最优性和鲁棒性,在本文建立的双馈风电机输出功率模型基础上,提出一种考虑风电机无功调节能力的配电网有功/无功联合调度方法。算例分析的结果表明,本文方法可以在保证系统安全稳定性的前提下减少额外无功设备的投入,且所得方案具有一定鲁棒性。
1 双馈风电机功率输出模型
基于目前的研究,本文所提出的考虑风速不确定性的双馈电风机的功率输出模型如图1所示。
图1中,线路热极限和励磁绕组热极限的表达式见文献[12-13],交点代表发电机的最大视在功率,在不考虑随机风速的情况下,发电机的输出功率必须位于点线以内。PE和PL分别代表由励磁绕组热极限和线路热极限决定的发电机可发出的最大有功功率;QE和QL分别代表对应的发电机可发出的最大无功功率。
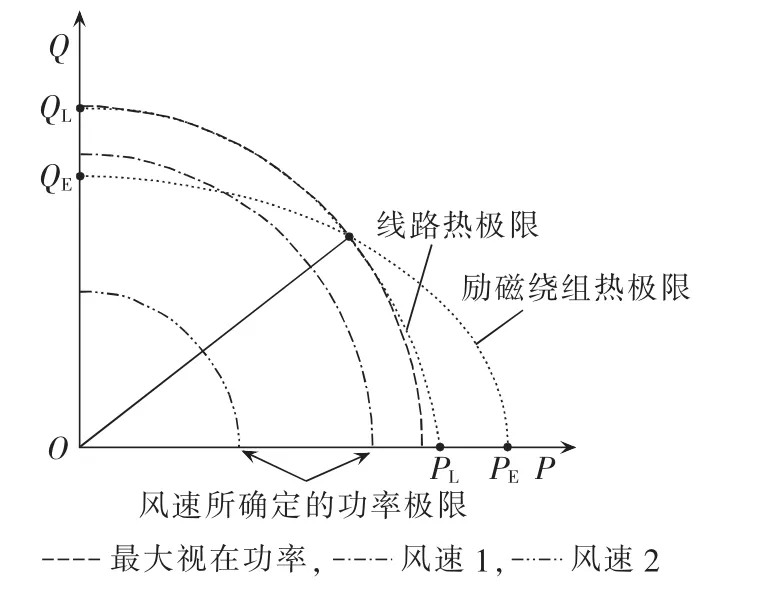
图1 双馈风电机输出功率模型Fig.1 Power output model of DFIG
对于普通发电机,由线路热极限和励磁绕组热极限所决定的区域已足以准确地描述发电机的输出功率空间。但风速的随机性可能导致风电机无法运行在最大视在功率。随着风速减小(风速1大于风速2),风电机的功率调节范围逐渐变小。本文将线路热极限、励磁绕组热极限及风速功率极限所决定的功率调整域作为风电机的运行域,风电机的输出有功/无功均必须位于该区域内。
下文为表述方便,将线路热极限、励磁绕组热极限共同决定的功率调整域定义为SH,而由风速决定的调整域定义为SF。同时,本文定义风电机最大视在功率随风速变化的规律为:
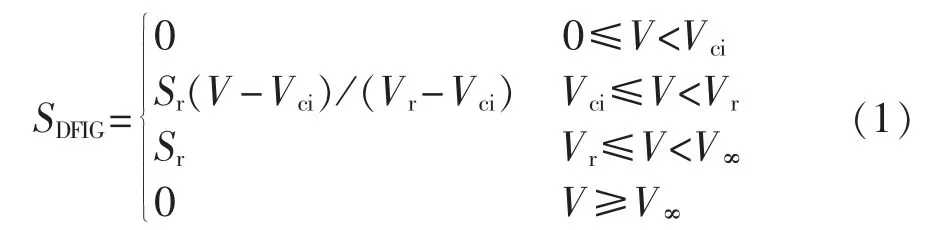
其中,SDFIG为风速V时风电机的最大视在功率;Sr为风电机的额定视在功率;Vci为切入风速;Vr为额定风速;V∞为切出风速。而有功/无功功率与视在功率满足下列关系:

其中,PDFIG和QDFIG分别为双馈风电机的输出有功功率及无功功率。通过本文模型,有功和无功功率可以在调整域内进行任意调整。
2 模型的建立
通过对风电机输出有功/无功的调整,本文以电压稳定裕度为目标,建立联合调度模型,如下所示。
a.目标函数:
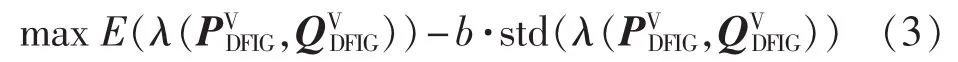
其中,E(λ)和 std(λ)分别为随机场景下电压稳定裕度的期望值及标准差;b为权重系数,为大于0的常数。E(λ)表征方法的最优性,而std(λ)代表方法的鲁棒性。通过优化如式(3)所示的目标函数,能够获得既具有较高电压稳定裕度,又具有较高鲁棒性的方案。
b.约束条件:
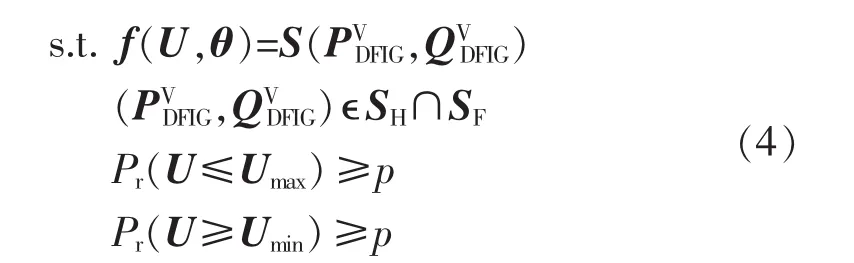
其中,f(U,θ)为系统潮流方程;为节点注入功率;U和θ分别为节点电压幅值和相角;Umax和Umin分别为节点电压约束的上、下限;p为特定概率,本文一般取为95%;Pr(·)表示求概率。第2个约束代表各风电机的输出功率向量必须处于第1节定义的功率调整域当中;第3、4个约束代表节点电压幅值的约束。
通过对风电输出有功/无功功率的调整,本文模型希望能获得电压稳定裕度更高的运行方案,从而保障系统的安全稳定运行。
3 模型的求解
根据前文,模型求解的难点主要在于功率调整域的判断和机会约束的转化。对于前者,伴随着风速的变化,发电机功率调整域会发生较大变化,在不同的风速区间,调整域由不同的部分组成,因此该调整域的判断过程对整个优化问题的求解效率具有较大影响,在第3.1节中,本文提出一种调整域判断方法。对于后者,机会约束的求解一直都是随机最优潮流的难点,在第3.2节中,本文提出一种极限松弛方法,将随机最优潮流问题解耦为普通潮流和随机潮流的迭代问题。
3.1 风电机输出功率约束判断
设任一风电机的输出有功/无功功率为(PDFIG,QDFIG),观察图1 可得,的最大值为,而当减小时,若满足大于等于或时,,此时发电机调整域为 SH∩SF;而当继续减小,使得小于和时,此时SF⊂SH,发电机调整域为SF。风电机输出功率约束判断流程可表示为如图2所示。
3.2 极限松弛方法
设节点电压幅值累积分布函数定义为 FH(z)=Pr{U<zEU},EU表示与 U 同维度的全 1 向量,则 U 的p-分位数集合为:
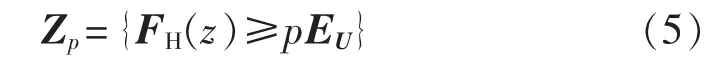
则式(6)的优化问题与含机会约束的最优潮流问题等价:

图2 风电机功率约束判断流程图Fig.2 Flowchart of wind turbine poweroutput constraint judgement
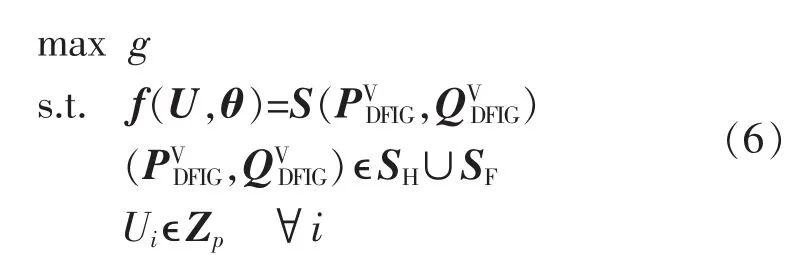
其中,g表示式(3)中目标函数。
因此确定Zp就是需要寻找累积分布函数的松弛因子a,使得U≤aEU与U∈Zp等价。但由于U的概率特性未知,确定a的准确数值十分困难,本文采用启发式的方法,给定松弛因子的初值a0将式(6)转化为确定型优化问题并求解,然后采用随机潮流获得最优运行点处的概率特性,利用该特性对松弛因子进行修正。利用两者的不断迭代生成序列an以逼近a,进而得到随机无功优化问题的松弛因子向量,使得U≤aEU、Pr(U≤zEU)≥p 和 Ui∈Zp(∀i)三者等价。
设第k次得到的p-松弛向量为ak(由ak1和ak2组合而成),则确定型优化的求解模型如式(7)所示。
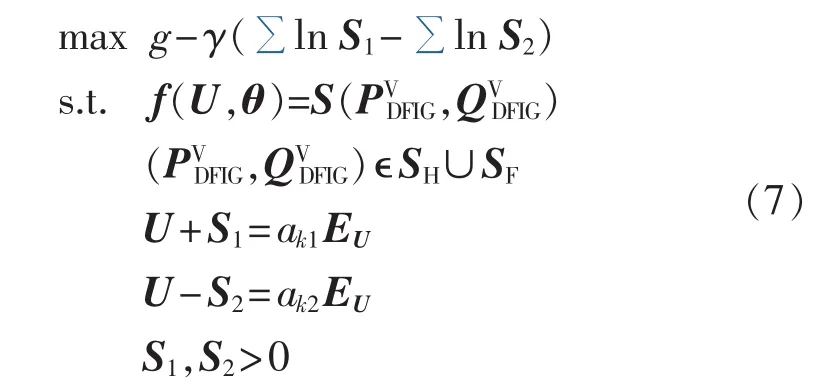
其中,S1、S2为松弛变量。式(7)可方便地采用内点法求解,其求解过程如图3所示。
ak的更新方法如下:

其中,ω为给定的系数。通过如式(8)所示的更新方式,可使得其逐渐逼近机会约束的可行域边界,从而将随机最优潮流问题转化为最优潮流和随机潮流的迭代过程,保证算法的收敛性和局部最优性。
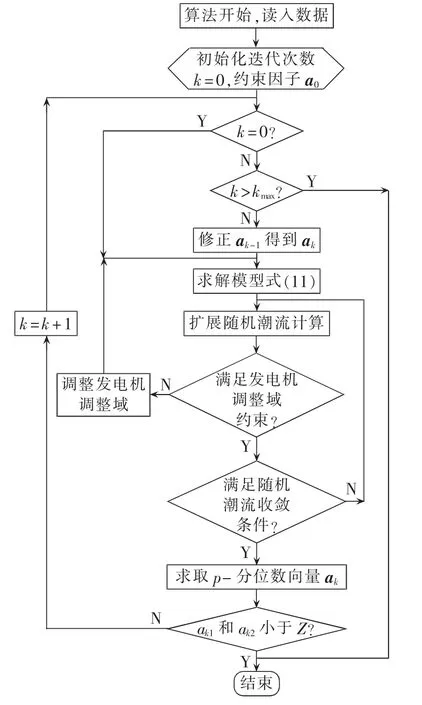
图3 算法流程图Fig.3 Flowchart of algorithm
4 算例分析
4.1 算例分析基础
本文利用IEEE 33节点系统作为测试算例,系统结构见图4。图4系统电压等级为12.66 kV,有功负荷为3715 kW,无功负荷为2300 kvar。假设各节点负荷均服从独立正态分布,期望等于负荷初始值,标准差为期望值的15%。切入风速为5 m/s,额定风速和切出风速分别为 8 m/s和 20 m/s,Weibull分布参数分别为2.0和8.5。系数b设为1。假设风电机安装在节点 21、11、14、17、24、32,单台风电机容量600 kW,kmax=20。
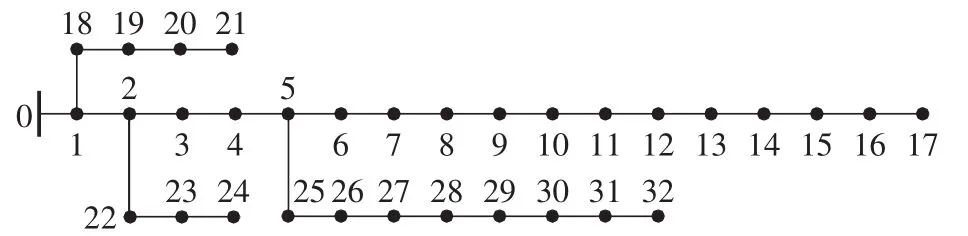
图4 33节点配电系统Fig.4 33-bus distribution network
4.2 有功/无功联合调度结果分析
4.2.1 优化结果
a.基态运行场景。
在基态运行中,负荷保持原始负荷不变,优化前后各节点95%和5%分位数曲线如图5所示(图中节点电压为标幺值)。为进一步分析本文所得方案的鲁棒性,优化前后所得电压稳定裕度概率密度函数如图6所示。
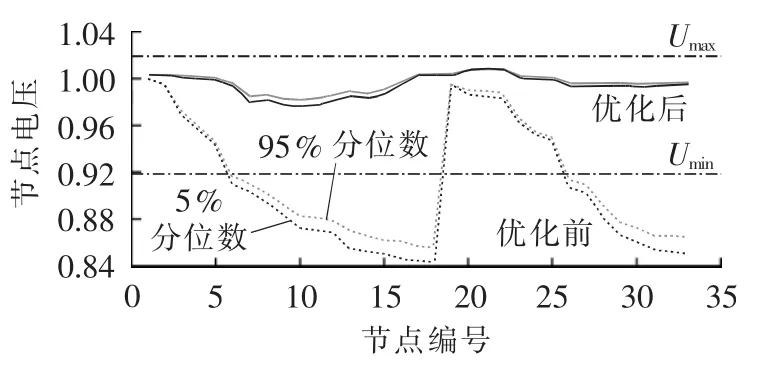
图5 优化前后节点电压分位数Fig.5 Quantiles of nodal voltage,before and after optimization
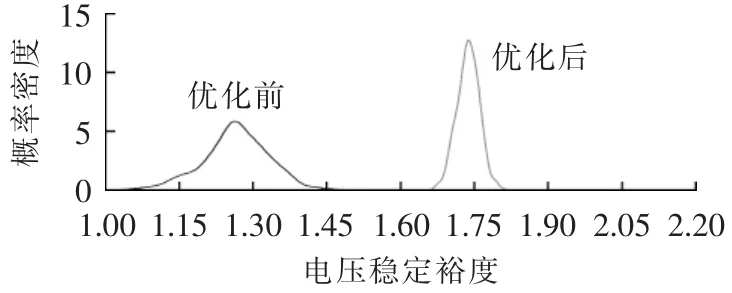
图6 优化前后电压稳定裕度概率密度函数Fig.6 Probability density functions of voltage stability margin,before and after optimization
对比图5中优化前后的曲线,可得如下结论:第一,优化后节点电压幅值的机会约束得到满足,这证明了本文极限松弛方法的有效性;第二,优化后各节点的电压均得到提高,系统的安全稳定水平得到保证;第三,节点电压的波动区间长度明显减小,这体现了本文方法所得方案具有一定的鲁棒性。
从图6可见,优化后系统的电压稳定裕度不仅提高,其方差也减小,这表明经过本文方法优化后,系统的运行风险减小,针对风电机出力随机性亦表现出更强的鲁棒性。
b.负荷增长场景。
为分析本文方法应对负荷增长的能力,分别对负荷因子为1.00、1.05、1.10的负荷场景进行计算,公共连接点(PCC)有功和无功交换的变化分别如表1所示。
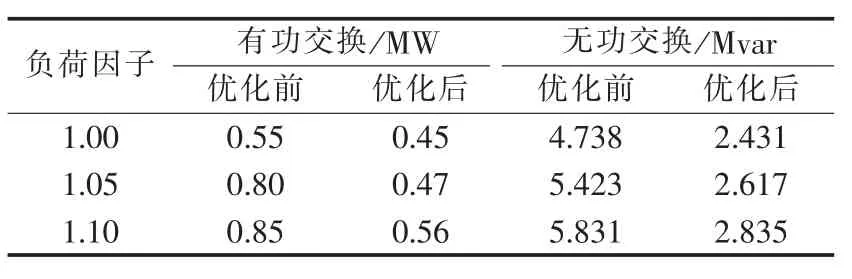
表1 各场景下PCC有功/无功交换Table 1 Active and reactive power exchanges of PCC for different scenarios
表1中,优化后PCC交换的有功/无功功率均减小。其中,有功交换减少主要原因是网络损耗减少,而无功交换减少主要因为风电机的无功输出,优化前该功率随着负荷增长不断增大,这非常不利于配电网的无功管理,无功的远距离传输也会增加系统的网络损耗。而经过本文方法优化后,交换无功功率随着负荷的增长变化不大,这说明通过合理利用风电机的无功调节能力,可以构建起更合理的配电网无功管理体系,同时也可减少投入系统的无功补偿设备。
4.2.2 风电机接入位置对系统影响
本节重点分析各台风电机接入位置不同时对系统的影响。第4.1节中设定的6台风电机接入位置较分散,在本文中称为分散式接入。本节设定风电机接入位置为节点 12、13、14、15、16、17,称为集中式接入,2种模式在基态时电压稳定裕度的概率密度函数如图7所示。
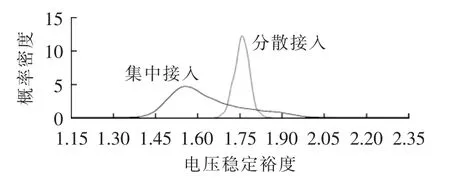
图7 2种模式下电压稳定裕度概率密度函数Fig.7 Probability density function of voltage stability margin for two modes
图7中,集中式接入下系统的电压稳定裕度期望值较低,且标准差大,系统运行的安全风险高。这主要是由于风电场过于集中,在局部区域内大量有功功率缺乏无功支撑,为保持系统稳定,大量无功功率被迫从远处传送至风电场区域内,这会导致系统其他区域缺乏无功支撑,直接导致系统的电压稳定裕度大幅度下降。因此在实际配电网运行中,风电机应该适当地分散接入以减小系统的运行风险,保障系统安全稳定地运行。
4.2.3 计算效率分析
本文所建立模型输入含机会约束的非线性优化问题,采用通常办法难以求解,目前主要的求解办法包括转化法[3]、模拟法[6]、近似法[2]。转化法首先利用随机潮流获得电力系统各状态变量的概率分布,并根据状态变量是否违反机会约束作为惩罚项,由于该转化过程没有解析表达式,因此转化法通常只有利用智能算法求解。近似法的思想是通过少量的确定型优化获得近似的随机最优潮流问题的解。其与转化法的区别在于:转化法在计算过程中将机会约束转化为确定型,整个计算过程中仅包含一次确定型优化;而近似法则需计算多次确定型优化,最终得到的是目标函数的矩信息。模拟法是采用蒙特卡洛法的思路,利用采样方法生成输入变量的样本,进行重复的确定型优化从而获得较精确的解。其过程与近似法相似,不同点在于样本点数目较多,即N较大,且直接通过计算所得序列的矩获得最优解的各阶矩而无需计算各点权重。
为体现本文方法的优势,本文所提出的机会约束极限松弛方法与转化法、模拟法和近似法进行比较。转化法采用混合蛙跳算法[14-15]SFLA(Shuffled Frog Leaping Algorithm),具体参数为SFLA参数:全局迭代次数100,局部搜索次数10,种群数200。模拟法采用扩展拟蒙特卡洛模拟法,初始模拟次数50次,步长增加50,收敛判据为方差系数小于5%。近似法采用常见的三点估计法。4种方法所得结果如表2所示,包括所得方案电压稳定裕度期望E(λ)、标准差 std(λ)、迭代次数 Tok及计算耗时 t。
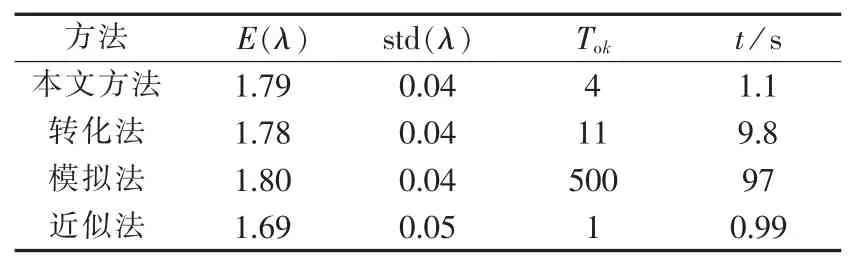
表2 4种方法所得结果Table 2 Results by four methods
从表2中数据可得,模拟法所得结果最准确,但计算效率较低,一般仅作为参考值提供;近似法计算效率最高,但容易陷入局部最优;本文方法与转化法所得结果类似,但计算效率远高于转化法。因此综合比较,本文方法既可保持较高的计算效率,又可以获得较优的结果,从而证明本文方法的有效性。
5 结论
针对目前风电机无功调节能力考虑不足的缺陷,本文建立考虑风电机无功调节能力的配电网有功无功2个调度模型,对IEEE 33节点系统的仿真证明了本文方法的有效性,得到结论如下:
a.本文方法可同时提高系统的电压稳定裕度,并减小电压稳定裕度的方差,这表明本文可同时提升系统的安全性并降低系统的运行风险;
b.通过本文方法优化后,PCC的无功交换大幅降低,这说明利用风电机的无功能力可以构建起合理的配电网无功管理方法;
c.对风电机集中式接入和分散式接入的研究表明,配电网中的风电机适合分散式接入,这样可以降低运行风险;
d.优化后节点电压幅值均满足约束,这说明本文提出的解耦法可以有效转化机会约束;
e.与其他求解含机会约束问题的方法相比,本文方法具有收敛速度快、计算效率高的特点。
[1]THOMAS A.Wind power in power systems[M].New York,USA:Wiley,2012:310-371.
[2]FANG Sidun,CHENG Haozhong,SONG Yue.Stochastic optimal reactive power dispatch method based on point estimation considering load margin[C]∥Proceedings of 2014 IEEE Power Engineering Society Genera l Meeting.Washington DC,USA:IEEE,2014:2231-2236.
[3]罗毅,多靖赟.基于量子免疫克隆算法的多目标无功优化[J].电力自动化设备,2013,33(9):31-35.LUO Yi,DUO Jingyun.Multi-objective reactive power optimization based on quantum immune colonial algorithm[J].Electric Power Automation Equipment,2013,33(9):31-35.
[4]孙伟伟,付蓉,陈永华.计及无功裕度的双馈风电场无功电压协调控制[J].电力自动化设备,2014,34(10):81-85.SUN Weiwei,FU Rong,CHEN Yonghua.Coordinated var and voltage controlofdoubly-fed wind farm considering reactive power margin[J].Electric Power Automation Equipment,2014,34(10):81-85.
[5]段建东,杨杉.基于改进差分进化法的含双馈型风电场的配电网无功优化[J].电力自动化设备,2013,33(10):123-127.DUAN Jiandong,YANG Shan.Reactive power optimization based on modified differential evolution algorithm for power distribution system with DFIG wind farms[J].Electric Power Automation Equipment,2013,33(10):123-127.
[6]ZOU Bin,XIAO Qing.Solving probabilistic optimal power flow problem using quasi Monte Carlo method and ninth-order polynomial normal transformation[J].IEEE Trans on Power Systems,2014,29(1):300-307.
[7]ROCKAFELLAR R T,ROYSET J O.On buffered failure probability in design and optimization of structures[J].Reliability Engineering and System Safety,2010,95(5):499-510.
[8]NIEDERREITER H.Quasi-Monte Carlo methods and pseudorandom numbers[J].Bull Am Math Soc,1978,84(6):957-1041.
[9]方斯顿,程浩忠,徐国栋,等.基于非参数核密度估计的扩展准蒙特卡洛随机潮流方法[J].电力系统自动化,2015,39(7):21-28.FANG Sidun,CHENG Haozhong,XU Guodong,et al.An extended quasiMonte-Carlo probabilistic load flow method based on non-parametric kernel density estimation[J].Automation of Electric Power Systems,2015,39(7):21-28.
[10]陈海焱,段献忠,陈金富.分布式发电对配网静态电压稳定性的影响[J].电网技术,2006,30(19):27-30.CHEN Haiyan,DUAN Xianzhong,CHEN Jinfu.Impacts of distributed generation on steady state voltage stability of distribution system[J].Power System Technology,2006,30(19):27-30.
[11]CHRISTOPHER S S.Point estimate method addressing correlated wind power for probabilistic optimal power flow[J].IEEE Trans on Power Systems,2014,29(3):1045-1055.
[12]EL-SAMAHY I,BHATTACHARYA K.A procurement market model for reactive power services considering system security[J].IEEE Trans on Power Systems,2008,30(1):137-149.
[13]FLORIN C.Assessing reactive power reserves with respect to operating constraints and voltage stability[J].IEEE Trans on Power Systems,2011,26(4):2224-2234.
[14]陈功贵,李智欢,陈金富.含风电场电力系统动态优化潮流的蛙跳算法[J].电力系统自动化,2009,33(4):25-30.CHEN Gonggui,LI Zhihuan,CHEN Jinfu.SFL algorithm based dynamic optimal power flow in wind power integrated system[J].Automation of Electric Power Systems,2009,33(4):25-30.
[15]方斯顿,程浩忠,宋越.考虑风电相关性的电力系统随机无功备用优化[J].电力自动化设备,2015,35(11):1-7.FANG Sidun,CHENG Haozhong,SONG Yue.Stochastic reactive powerreserve dispatch method considering correlated wind power[J].Electric Power Automation Equipment,2015,35(11):1-7.
