带弹性放大器的双稳态压电振动能量采集器*
2017-05-24杨斌强徐文潭王学保李秀玲王光庆
杨斌强,徐文潭,王学保,李秀玲,王光庆
(浙江工商大学信息与电子工程学院,杭州 310018)
带弹性放大器的双稳态压电振动能量采集器*
杨斌强,徐文潭,王学保,李秀玲,王光庆*
(浙江工商大学信息与电子工程学院,杭州 310018)
针对带弹性放大器的双稳态压电振动能量采集器,利用Hamilton原理和 Raleigh-Ritz方法建立了压电振动能量采集器的机电耦合分布参数模型。重点分析了激励频率Ω≥1时系统质量比、刚度比、磁铁对间距等参数对系统输出性能的影响。研制了压电振动能量采集器原理样机,搭建了实验测试平台,实验测试了压电振动能量采集器的输出性能。研究结果表明带弹性放大器的压电振动能量采集器是一个非线性双自由度系统,具有两个双稳态运动区域;在激励频率Ω≥1时压电振动能量采集器需要较大的激励能量才能进入大幅值周期振动状态。
双稳态压电振动能量采集器;弹性放大器;分布参数模型;仿真与实验
振动能量采集器是一种能将环境中的振动能转化为电能的机电转换器件,在微能源和自供电系统中有广泛的应用前景。譬如,它可以解决无线传感网络和MEMS器件中使用电池供电的诸多弊端,如生命周期短,环境污染等。压电振动能量采集器PEH(Piezoelectric Energy Harvester,)结构简单,制造容易,能量转换密度高,成为研究热点[1]。然而传统的压电能量采集器一般被设计成线性系统,工作频带窄,谐振频率难以和环境振动频率完全匹配,致使能量采集与转换效率大大降低[4]。
为了克服线性压电振动能量采集器的缺陷,在宽频带内产生足够能量,双稳态压电能量采集器BPEH(Bistable Piezoelectric Energy Harvester,)[5]被提出。大部分现有的双稳态能量采集器都是通过两块永磁体之间的排斥力来实现,基本结构如图1(a)所示。双稳态系统具有独特的双陷回复力势能特性,即势能函数具有两个势阱和一个势垒,当外界振动能量小于势垒值时,系统将在其中一个势阱附近振动;当外界振动能量大于势垒值时,系统将跨越势垒,在两个势阱之间作大幅值的周期振动,这时系统的输出响应得到显著提升[8]。例如,Lihua Tang[11]等设计了一种自由端磁铁块带有磁力振荡器的双稳态能量采集器,实验表明改进的双稳态能量采集器工作频带扩宽了近一倍,输出性能也提高了41%。高毓璣[12]等提出外部磁铁弹性支撑的结构,实验指出,对于强度变化的随机激励,弹性支撑非线性能量采集系统不需要实时调整磁铁间距,就能实现高效的机电能量转换。Pilkee Kim[13]等提出了一种三稳态能量采集器,具有更浅和宽的势能阱,能在低能激励下有效采集能量。Noha[14]等在双稳态采集器基础上通过微控制器监测振源频率,通过步进电机用控制算法来查表优化调整原固定端的磁铁位置,从而自动调整系统谐振频率来提高输出性能。然而,双稳态压电振动能量采集器严重依赖外部振动源激励幅值的特点,并不能使它的输出性能得到极大地提高。通常,环境中的振动往往是比较微弱的,输入到双稳态能量采集器的激振能量无法使它跨越势垒的阻碍作用,只能在某个势能阱内做小幅值的低能轨道振动,此时,双稳态能量采集器与线性采集器的输出特性相似。
为克服此现象,文献[15]利用磁场增强与弹性放大技术构建了一种带弹性放大器的双稳态压电振动能量采集器(BPEH+EM),考虑采集器一阶谐振特性,建立了能量采集器的集总参数模型,分析了频率范围Ω<1时系统参数对能量采集器输出特性的影响,研究表明通过弹性放大器对基础激励的放大作用,可以使双稳态压电振动能量采集器在低幅值激励条件下轻松作大幅值周期振动,达到改善其输出性能的目的。但集总参数模型忽略了压电悬臂梁的分布参数和动态振型对输出性能的影响,且文献主要研究了采集器在频率范围Ω<1时的输出特性,而Ω≥1时的情况未有考虑。本文考虑振型和分布参数的影响,在文献[15]的基础上利用Hamilton原理建立了机电耦合分布参数模型,重点研究了采集器在频率范围Ω≥1时,系统质量比、刚度比、磁铁对间距等参数对系统输出性能的影响,实验验证了理论分析结果的正确性。
1 系统结构
图1(b)是BPEH+EM的结构原理示意图,它由双稳态压电悬臂梁振动能量采集器和一个弹性放大器组成,弹性放大器置于双稳态压电能量采集器与基座之间,且它们之间为理想粘结。一对永磁铁分别相对固定于悬臂梁末端和支架上,两个永磁体磁场相反,相互产生排斥力。图1(b)所示BPEH+EM结构可以简化成图2所示的物理模型,两压电陶瓷(PZT1和PZT2)分别对称粘结在金属基板的上下表面,且在z轴方向的极化方向相反。RL为输出负载电阻。Mb、Kb、Cb是分别是弹性放大器的质量、弹簧刚度和阻尼系数。L是悬臂梁的长度,b是悬臂梁宽度。hp和hs分别为PZT厚度和基板厚度。两永磁体磁铁块的间距为d,且两者质量都为Mt。
假定压电片与金属基板是完好粘结的,且压电悬臂梁为Euler-Bernoulli梁。则此模型中金属基板满足本构关系
σs=csεs
(1)
压电片PZT满足本构关系
(2)


图1 BPEH与BPEH+EM结构原理示意图

图2 简化的BPEH+EM物理模型
2 机电耦合分布参数模型
根据Hamilton原理,该模型的运动方程为
(3)
式中:t为时间;T为系统动能;U为系统势能;We为电势能;W为外力做功。
2.1 系统动能T
系统动能T由弹性放大器动能Tb、金属基板动能Tks和压电片动能Tkp以及悬臂梁末端磁铁块动能Tt组成。根据Raleigh-Ritz方法,压电梁的相对横向弯曲位移可以写成[16]:
(4)
式中:φri(x)为悬臂梁弯曲振型函数;ri(t)为与时间相关的i阶坐标;nr为振型个数。
假定悬臂梁振动只表现为一阶振型,且一阶振型函数为
φ(x)=C[cosγx-coshγx+σ(sinγx-sinhγx)]
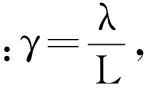
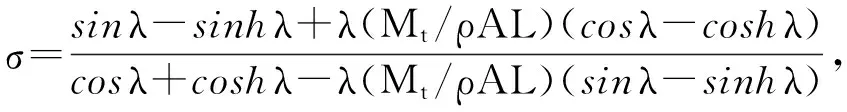
(5)
式中:It为悬臂梁末端磁铁块绕其质心的转动惯量。
假设ZM(t)为弹性放大器输出位移,则压电梁位移为y(x,t)=w(x,t)+ZM(t)。因此,系统动能可表示为:
(6)
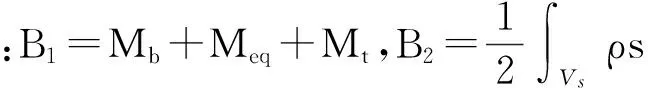
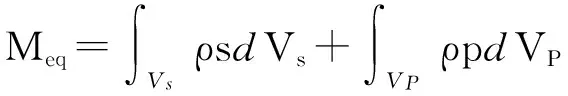
2.2 电势能We
根据Raleigh-Ritz方法,压电悬臂梁的电势为
(7)
式中:ψVj(x)为第j对电极沿z向的电势分布函数;vj(t)为与时间相关的第j对电极电压。
(8)
式中:z是沿压电梁厚度方向坐标。
两个压电片的两端电势差分别为
(9)
式中:V1为PZT1输出电压;V2为PZT2输出电压,且V1=V2。
(10)
压电梁轴向应变为
S(x,t)=-zφ″(r)r(t)
电势能为
(11)

2.3 外力做功δW
外力做功为
(12)
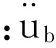
2.4 系统势能U
系统势能U由弹性放大器势能UZM和金属基板势能Us和压电片势能Up还有非线性势能Um组成。
非线性势能Um可以根据磁力模型得到,磁力模型具体见参考文献[17],根据悬臂梁末端扰度为w(L,t),可得到
(14)
将w(L,t)=φ(L)r(t)代入上式,可以得出磁力
Fm=k1r-k3r3式中:k1= [12φ2(L)+2d2φ′2(L)+6dφ(L)φ′(L)]k/d5
k3=[45φ4(L)+3d4φ′4(L)+12d2φ2(L)φ′2(L)+
6d3φ(L)φ′3(L)+30dφ5(L)φ′(L)]k/d7
将式(6)、式(11)~式(13)代入到Hamilton运动方程中,加入机械阻尼,由 Lagrange方程可得出其非线性运动微分方程为
(15)
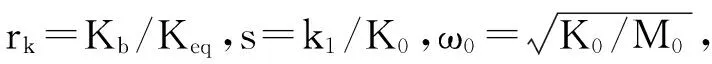
(16)
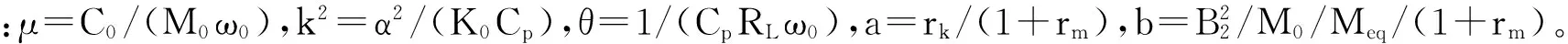
将式(16)转换成状态空间方程形式得:
(17)

3 系统解分析
3.1 频域解析
利用谐波平衡法对式(16)进行频域求解,忽略高次谐波信号,可以得到一个关于振动幅值A的六阶非线性多项式:
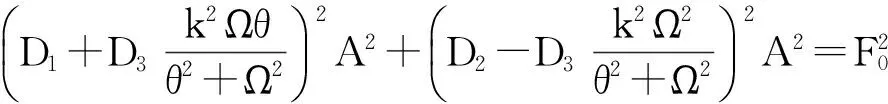
(18)

a0、a1和a2为采集器振动位移表达式R(τ)=a0(τ)+a1(τ)cosΩτ+a2(τ)sinΩτ的系数。解式(18)可得到3个关于振动幅值A的解,其中只有最大和最小的2个解是稳定的、且可实现的,这也意味着整个能量采集器系统在给定的激励频率和幅值下具有2个稳定的谐振运动。

图3 系统幅值响应随激振频率的变化
取仿真参数u=0.04,θ=1.095 1,k2=0.411,s=1.135 1,激励幅值F0=0.05,系统初始运动条件x1(0)=0.367 5,x2(0)=x3(0)=x4(0)=x5(0)=0。不同rm、rk下,悬臂梁末端位移随激励频率的变化情况如图3所示。可见,BPEH+EM是一个两自由度非线性系统,幅频响应曲线存在2个谐振峰值,在磁铁对非线性排斥力的作用下,这2个峰值均向右倾斜。随着rm、rk的增大,系统幅值也增大,且两个峰值间的频率间距缩小形成一个宽频窗口。另外,采集器存在两个区域可以使得系统做大幅值的高能轨道振动,一是激励频率在0.5<Ω≤1区域,二是激励频率在1<Ω≤1.2区域。
3.2 时域解析
根据系统的状态空间方程式(17)在MATLAB软件中利用4阶、5阶龙格库塔算法ODE45进行数值求解,得到系统在不同初始条件和不同参数下的时域解,如末端振动位移,输出电压和相图等。
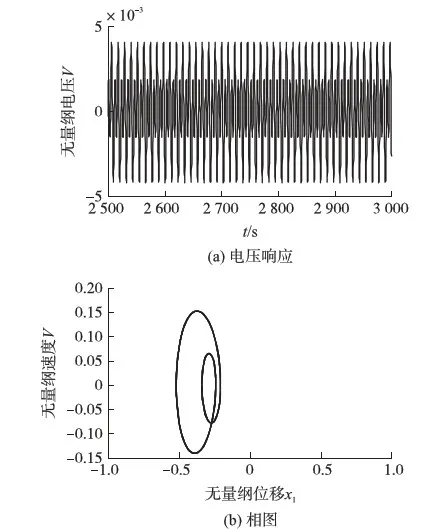
图4 F=0.01时系统的无量纲电压和相图
文献[15]研究了激励频率0.5<Ω≤1区域时,系统质量比、刚度比等对能量采集器输出特性的影响。在激励频率Ω=0.8时,当质量比和刚度比rm=rk=1时,由于弹性放大器的放大作用较小,系统末端绕平衡位置做小幅值的周期振动,因此系统振动位移,振动速度和输出电压均比较小。当质量比和刚度比rm=rk=3时,悬臂梁末端开始在2个势能陷之间作混沌运动,并产生混沌的电压响应。当继续增大rm=rk=[6,10]时,系统出现进入瞬时的混沌运动后,进入大幅值周期的高能轨道运动,此时系统振动位移,振动速度和输出电压大幅增加。当rm=rk=16时系统完全进入大幅值周期的高能轨道,输出性能大幅提升。本文重点研究激励频率1<Ω≤1.2时系统质量比、刚度比等对采集器输出特性的影响,取激励频率Ω=1.1,仿真参数u=0.04,θ=1.095 1,k2=0.411,s=1.135 1,系统初始运动条件x1(0)=0.367 5,x2(0)=x3(0)=x4(0)=x5(0)=0。为了节省篇幅,这里只研究rm=rk=16时不同激励幅值条件下压电能量采集器的振动特性和采集输出电压,如图4~图6所示。
当激励幅值F=0.01时,压电能量采集器绕着静平衡位置x1=-0.367 5作小幅值的倍周期振动,如图4所示,此时采集器末端振动位移、振动速度和采集输出电压都很小;当激励幅值增大到F=0.5时,压电能量采集器作大幅值的混沌运动,产生混沌的振动位移、振动速度和采集输出电压,如图5所示;继续增大激励幅值到F=0.9,此时,压电能量采集器开始做大幅值的双稳态周期振动,进入高能轨道运动状态,产生大幅值周期电压、振动位移和速度,如图6所示。

图5 F=0.5时系统的无量纲电压和相图

图6 F=0.9时系统的无量纲电压和相图
与激励频率Ω=0.8时的输出特性相比较,在相同的质量比和刚度比条件下,激励频率Ω=1.1时压电能量采集器作大幅值的双稳态周期振动所需的激励幅值大大增加。这主要是由于外部磁力作用在压电能量采集器末端,使得压电能量采集器的谐振频率Ωn降低至Ω0,激励频率Ω=0.8比较接近Ω0,在较小的外部激励作用下,更容易产生谐振进入大幅值振动状态,而激励频率Ω=1.1则远离Ω0,因此,需要较大的外部激励才能使其进入大幅值振动状态。
3.3 质量比、刚度比对位移幅值的影响
图7为系统末端振动位移幅值随质量比、刚度比的变化情况,由图7可知,质量比、刚度比rm、rk较小时,采集器悬臂梁末端绕着中心平衡位置做小幅值周期运动,末端位移幅值只有1个稳态解。当质量比、刚度比rm、rk逐渐增大到2.5时,末端位移曲线开始出现分叉现象,表明系统末端开始做混沌运动以及大幅值周期运动,这时采集器悬臂梁末端位移出现3个解,这与时域分析中结果是一致的。可见,增大rm、rk有利于系统作大幅值周期运动,提高系统能量采集输出性能。

图7 系统幅值响应随rm、rk的变化
3.4 磁铁对间距对位移幅值的影响
保持其他参数不变,当rm、rk确定时,分析磁铁对间距dr(定义dr=d/L)对末端振动位移的影响,结果如图8所示。

图8 系统幅值响应随磁铁对间距dr的变化
由图8可以看出,当磁铁对间距相对较小时,因为无法逃脱非线性势能的势垒,采集器悬臂梁统末端绕中心平衡位置做小幅值周期运动。当磁铁对间距增大到适当距离,图中曲线开始出现分叉,表明系统开始做双稳态大幅值周期运动。当磁铁对间距越来越大直至无穷远,此时,磁铁对的非线性势能对采集器悬臂梁的作用消失,系统只受到弹性放大器的线性放大作用,质量比与刚度比越大,系统末端振动位移幅值也越大。在rm=rk=1时,系统末端只在间距dr=[0.28,0.31]之间做大幅值周期运动;而rm=rk=16时,系统末端在间距dr=[0.30,0.39]之间做大幅值周期运动。可见,增大质量比和刚度比,系统作大幅值周期运动的磁铁间距范围也增大了,这说明能量采集器更容易地进入高能轨道振动状态,且具有更大的位移幅值。
3.5 分叉分析
图9是能量采集器静态分岔行为分析结果,当磁铁对间距d大于分叉点间距(d0=18 mm)时,磁铁对的非线性势能对采集器的作用较小,能量采集器变为一个单稳态系统,只存在一个稳定解;当d减小18 mm时,系统变为不稳定,开始分岔,出现两个稳定的非平凡解和一个不稳定的解,且两个稳定解的距离随d的减小先增大后减小,由此可知,从单稳态能量采集系统变成双稳态能量采集系统需要经过一个叉形分叉。
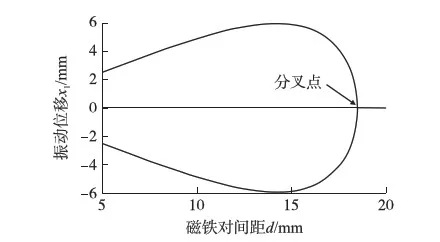
图9 分叉分析
4 实验与结果分析
图10是BPEH+EM能量采集器样机和实验测试装置。实验中,BPEH+EM能量采集器样机通过高强度胶粘结固定在激振器的安装台面上,信号发生器(Agilent 33120A)产生的正弦信号经功率放大器(B&K 2706)放大后,驱动激振器(B&K 4810)模拟基础做简谐振动,基础加速度由加速度计(B&K 4513-001)测量得到,采集器悬臂梁末端振动位移由激光测振传感器(PolyTec CFV303)测量得到,采集输出电压由双通道示波器测量显示。首先测得压电悬臂梁的谐振频率为20 Hz,加上磁铁对后压电悬臂梁的谐振频率为16.2 Hz。为了与理论分析一致,实验过程中取激励频率为22 Hz(Ω=1.1)。

图10 实验测试系统与BEPH+EM样机
文献[15]实验验证了激励频率为16 Hz(Ω=0.8)时,弹性放大器的引入,可以提高能量采集器的输入能量,克服势能阱的势垒,使得双稳态能量采集器在较小的基础加速度下也能顺利进入双稳态震荡状态,实现大幅值周期运动,且具有更宽的大幅值周期振动频带,如图11所示。
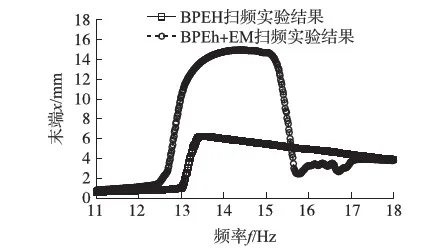
图11 BPEH+EM与BPEH扫频实验对比结果
本文重点测试了激励频率22 Hz(Ω=1.1)时,采集器在不同激励加速度作用下的输出电压、末端振动位移和速度的变化情况,如图12所示。由图12可以看出,当激励加速度小于30 m/s2时,能量采集器绕着中心平衡位置作小幅值周期振动,此时采集输出电压、振动位移和振动速度都比较小;逐渐增大激加速度到53.5 m/s2,压电能量采集器在经历混沌振动后,进入大幅值周期振动状态,作高能轨道的双稳态振动,此时系统的采集输出电压、振动位移和振动速度都大大提高,这一实验现象与理论分析结果是一致的。与文献[15]研究结果相比可以发现,激励频率22 Hz时采集器作大幅值周期运动所需的激励加速度大幅提高,这是由于此时的激励频率远离采集器的谐振频率16.2 Hz(考虑磁铁排斥力时)。

图12 激励频率22 Hz时能量采集的输出性能实验结果
5 结论
利用Hamilton原理和Raleigh-Ritz方法建立了带有弹性放大器的双稳态压电振动能量采集器分布参数机电耦合模型,通过仿真与实验研究,得到以下主要结论:①带用弹性放大器的双稳态压电振动能量采集器是一个非线性双自由度系统,存在两个双稳态运动区域,一是激励频率0.5<Ω≤1,此区域压电能量采集只需较小的外部激励加速度作用就可以作大幅值的双稳态运动;二是激励频率1<Ω≤1.2,此区域压电能量采集器需要较大的外部激励加速度才能作大幅值的双稳态运行。②增加BPEH+EM的质量比和刚度比,可以使能量采集器更容易地进入大幅值周期振动状态,且具有更大的位移幅值和更宽的工作频带。
致谢
本文在实验研究方面得到了香港中文大学智能材料与结构实验室廖维新教授团队的大力支持与帮助,在此表示衷心感谢。
[1] Roundy S,Leland E S,Baker J,et al. Improving Power Output for Vibration-Based Energy Scavengers[J]. IEEE Pervasive Computing,2005,4(1):28-36.
[2] Dutoit N,Wardle B L,Kim S G. Design Considerations for MEMS-Scale Piezoelectric Mechanical Vibration Energy Harvesters[J]. Integrated Ferroelectrics,2005,71(1):121-160.
[3] Sodano H A,Park G,Inman D J. Estimation of Electric Charge Output for Piezoelectric Energy Harvesters[J]. Strain,2004,40(2):49-58.
[4] 李萧均,王光庆,杨斌强. 基于弹性支撑与放大的宽频压电振动能量采集器模型与实验研究[J]. 传感技术学报,2016,29(5):693-699.
[5] Erturk A,Hoffmann J,Inman D J. A Piezomagnetoelastic Structure for Broadband Vibration Energy Harvesting[J]. Appl Phys Lett,2009,94:254102.
[6] Erturk A,Inman D J. Broadband Piezoelectric Power Generation on High-Energy Orbits of the Bistable Duffing Oscillator with Electromechanical Coupling[J]. Journal of Sound and Vibration,2011,330:2339-2353.
[7] 王光庆,张伟,刘创,等. 非线性压电振动能量采集器的振动特性与实验研究[J]. 传感技术学报,2015,28(10):1494-1501.
[8] 代显智,张章,刘小亚. 非线性宽频振动能量采集技术的研究进展[J]. 中国科学:技术科学,2016,46(8):791-807.
[9] Mann B P,Owens B A. Investigations of a Nonlinear Energy Harvester with a Bistable Potential Well[J]. Journal of Sound and Vibration,2010,32(9):1215-1226.
[10] Stanton S C,Owens B A,Mann B P. Harmonic Balance Analysis of the Bistable Piezoelectric Inertial Generator[J]. Journal of Sound and Vibration,2012,33(1):3617-3627.
[11] Lihua Tang,Yaowen Yang. A Nonlinear Piezoelectric Energy Harvester with Magnetic Oscillator[J]. Applied Physics Letters,2012,101:094102.
[12] 高毓璣,冷永刚,范胜波,等. 弹性支撑双稳压电悬臂梁振动响应及能量采集研究[J]物理学报2014,63(9):090501.
[13] Pilkee Kim,Jongwon Seok. Dynamic and Energetic Characteristics of a Tri-Stable Magnetpiezoelastic Energy Harvester[J]. Mechanism and Machine Theory,2015,94:41-63.
[14] Noha A Aboulfotoh,Mustafa H Arafa,Said M Megahed. A Self-Tuning Resonator for Vibration Energy Harvesting[J]. Sensors and Actuators A,2013,201:328-334.
[15] Wang G Q,Liao W X. A Bistable Piezoelectric Oscillator with an Elastic Magnifier for Energy Harvesting Enhancement[J]. Journal of Intelligent Material Systems and Structures,2016,28(3):392-407.
[16] Erturk A,Inman D J. A Distributed Parameter Electromechanical Model for Cantilevered Piezoelectric Energy Harvesters[J]. Journal of Vibration and Acoustics,2008,130:2-15.
[17] 唐炜,王小璞,曹景军. 非线性磁式压电振动能量采集系统建模与分析[J]. 物理学报,2014,63(24):240504.
A Bistable Piezoelectric Vibration Energy Harvester with an Elastic Magnifier*
YANG Binqiang,XU Wentang,WANG Xuebao,LI Xiuling,WANG Guangqing*
(School of Information and Electronic Zhejiang Gongshang University,Hangzhou 310018,China)
Focusing on the BPEH(Bistable Piezoelectric vibration Energy Harvester)with an EM(Elastic Magnifier),the coupling electromechanical distributed parameter model was established with Hamilton principle and Raleigh-Ritz method. The effects of the mass ratio,stiffness ratio,and the distance of magnets on the output performance were extensively analyzed when the exciting frequency isΩ≥1. The prototype of the new BPEH and the experiment setup were developed,some experiments were carried out to exhibit the output performance. The results show that the new BPEH is a two-degree-of-freedom nonlinear system,which has two bistable motion regions. In the region ofΩ≥1,it will oscillate in a large-amplitude high-energy orbit motion excited by large acceleration amplitude.
bistable piezoelectric vibration energy harvester;elastic magnifier;distributed parameter electromechanical model;simulation and experiments

杨斌强(1993-),男,硕士研究生,主要从事压电振动能量采集方面的研究工作,276203299@qq.com;

王光庆(1975-),男,博士,教授,主要从事传感检测与信号处理、压电超声驱动器、压电振动能量采集器的理论与应用研究,kele76@163.com。
项目来源:国家自然科学基金项目(51277165);浙江省自然科学基金项目(LY15F010001)
2016-10-19 修改日期:2017-02-09
TH825
A
1004-1699(2017)05-0684-08
C:7230
10.3969/j.issn.1004-1699.2017.05.009
