穿浪双体船迎浪纵向运动和阻力增值CFD不确定度分析
2017-05-24白伟宾刘浩然周立学
赵 帅,白伟宾,周 帅,刘浩然,周立学
穿浪双体船迎浪纵向运动和阻力增值CFD不确定度分析
赵 帅,白伟宾,周 帅,刘浩然,周立学
(海军工程大学,武汉430033)
基于RANS方法,对穿浪双体船浪(WPC)迎浪纵向运动和阻力增值进行了数值分析,并对计算数值进行了验证和确认,证明了静水和波浪中运动计算结果的可靠性。通过计算结果与模型试验数据的对比发现,RANS方法在各种波长中预报精度均较高,验证了该方法的有效性。
穿浪双体船 波浪中运动 阻力增值 RANS
0 引言
CFD方法考虑了粘性作用、非线性因素、波浪破碎及湍流的作用,还能够给出复杂流场信息,克服了势流方法的缺点。近年来,随着计算机的快速发展和CFD模拟技术的完善,RANS方法被越来越多地被应用于船舶研究领域。Castiglione等[1]利用CFDShip-Iowa求解器计算了DELFT372双体船以不同速度在波浪中的运动,并把计算结果与切片理论的计算结果进行了对比。Carrica等[2]使用上述求解器对KCS模型进行了静水及波浪中的自航模拟,与实验结果对比发现运动的计算精度远高于阻力的计算精度。Guo等[3]进行了不同波长中的验证与确认研究,结果表明所有波长中的运动和阻力增值的预报精度较高。Simonsen等[4]对带附体的KCS模型在静水和波浪中的运动、流场和阻力进行了模型试验及数值分析,主要研究了大幅度运动、响应峰和最大激励条件等。与势流理论的计算结果及实验结果的对比显示RANS方法具有更高的精度。Sadat- Hosseini等[5]使用RANS方法分别预报了释放和拘束纵荡时KVLCC2在短波和长波中的运动和阻力增值,并与实验数据进行了对比。Qian等[6]使用RANS方法对带有倾斜支柱的SWATH船进行分析,计算结果与试验数据较为吻合。Tezdogan等[7]使用RANS方法对全尺寸KCS模型在一系列规则波中处于设计航速和减速航行时的运动和阻力增值进行了预报,计算结果与试验数据较为吻合。
与传统计算方法相比,CFD在准确预报船舶的耐波性能方面体现出巨大优势,但该方法对于穿浪双体船耐波性的计算精度还未得到系统研究。为此,本文以某型穿浪双体船为研究对象,基于CFD技术,建立了其波浪中运动及阻力增值数值计算方法,并把计算结果与试验结果进行对比,对计算进行不确定度分析。同时,对不同波长中船体运动对阻力增值的贡献进行进一步分析。
1 试验模型与试验条件
本文试验和数值计算所用模型的主要船型参数为:2.667 m69.400 kgk=0.255m。三维图如图1所示。

图1 船体三维图
试验波高取50 mm,在3.2~11.2 m之间取11个波长进行迎浪航行试验,试验中用升沉位移仪测量升沉,用陀螺仪测量纵倾角,用电测阻力仪测量波浪中阻力增量。
2 控制方程及计算方法
2.1 船体粘性流场计算方程
RANS方程是粘性流体运动学和动力学的控制方程,文中以它作为求解船体粘性兴波流场的基本方程。其具体形式如下:
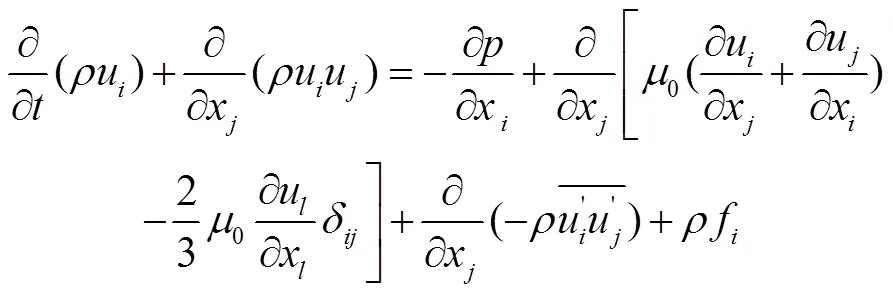
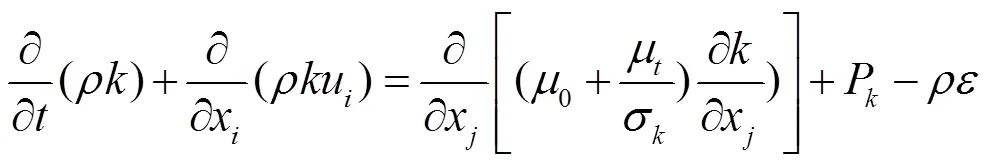
(3)
采用流体积法计算船体兴波。
2.2船体运动求解
波浪中船模所受力和力矩为
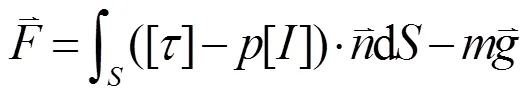
(5)
根据牛顿第二定律,船模运动的六自由度控制方程表达式如下:
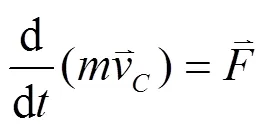
(7)
在数值模拟中,作用在船模上的力和力矩可由式(4)、(5)得到,其运动的速度、角速度及位置、姿态等可以通过式(6)、(7)求解、积分得到[8]。
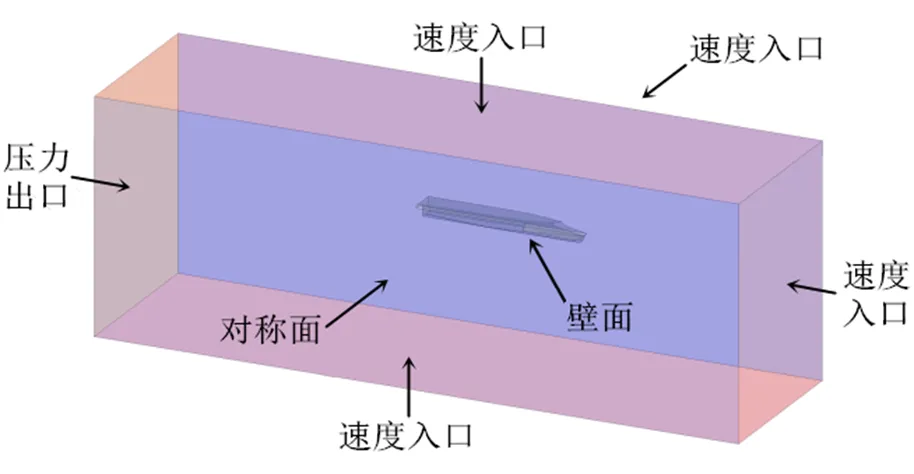
图2 边界条件
2.3 计算区域及网格划分
计算区域为-2<<2,0<<3.75,-<<0.4,中纵剖面位于=0,基线位于=0,尾封板位于=0。由于船体左右两舷对称,为减少计算量,只需计算一半船体。计算区域的边界条件为:入口、顶部、底部、远离船体的侧壁设定为速度入口,靠近船体的侧壁设定为对称面,出口设定为压力出口,船体设定为壁面,如图3所示。
网格划分采用非结构化网格,为捕捉自由面求解和船体附近复杂流动,对自由面及船体附近网格进行加密,网格划分如图4所示。
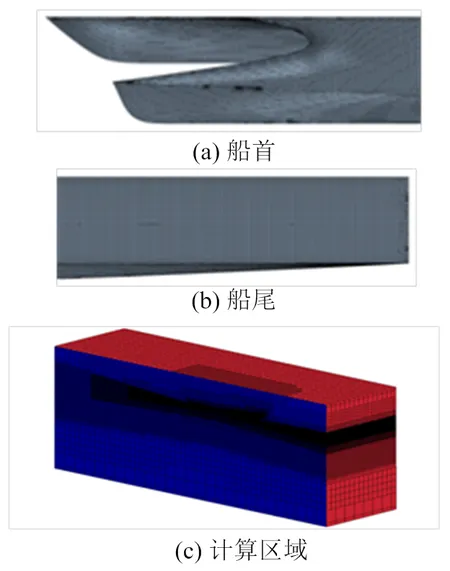
图3 计算网格
3 CFD不确定度分析
CFD中的不确定度分析由验证和确认两个过程组成。误差和不确定度的定义与试验不确定度分析一样。数值模拟结果与真值之差即为数值模拟误差,它由模型误差和数值误差两部分组成,即

(9)
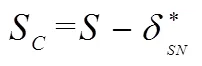
(11)
对于修正过的数值模拟方法,对解进行修正,可以得到数值基准。数值误差的估计值和修正值的不确定度可以由下式给出

(13)
确认的定义是利用基准试验数据评估数值模拟的建模不确定度U的过程,并且当条件允许时,还要估计模型误差δ自身的符号和大小。对比误差由试验数据和模拟值相减得到
通过比较和确认不确定度U来判定确认实现与否,其中
(15)
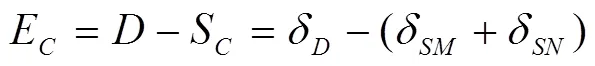
(17)
以上为不确定度分析的基本流程,具体步骤见文献[9]。
4 计算结果分析
4.1 静水中阻力与运动CFD不确定度分析
4.1.1 验证
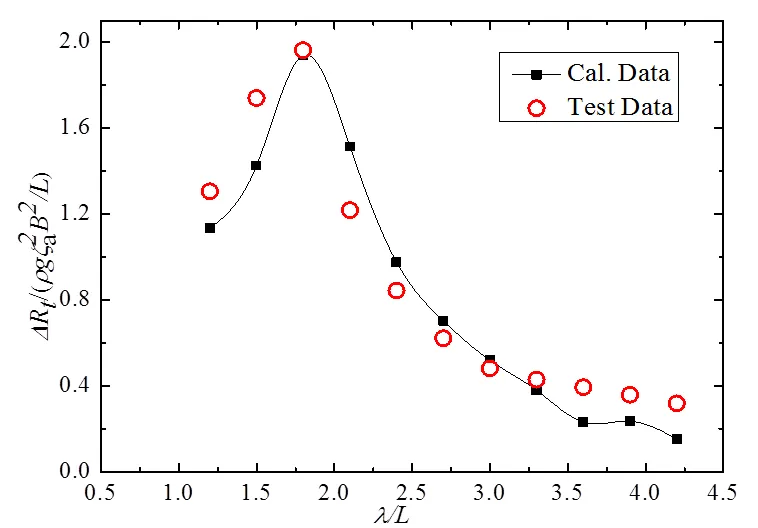
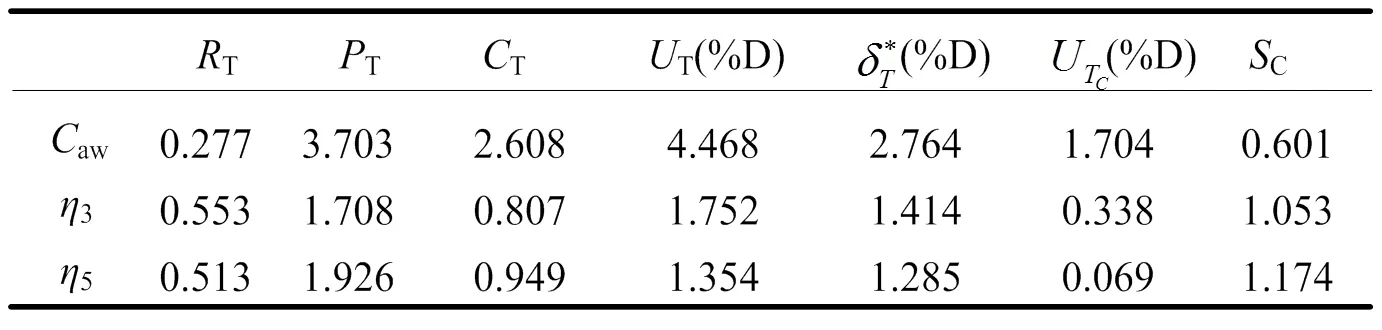
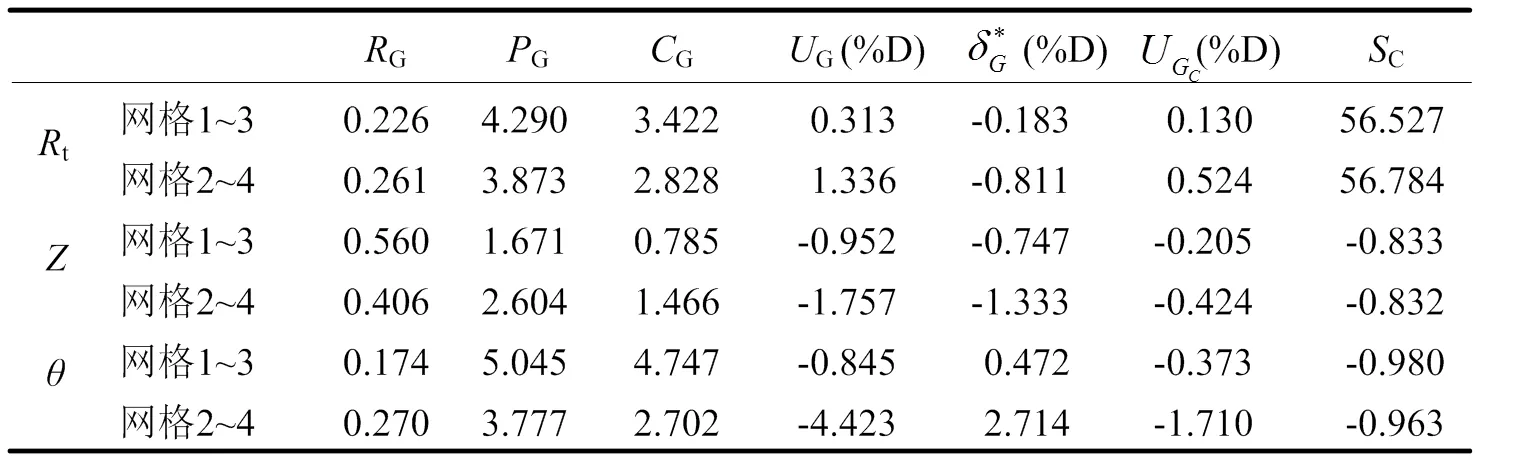
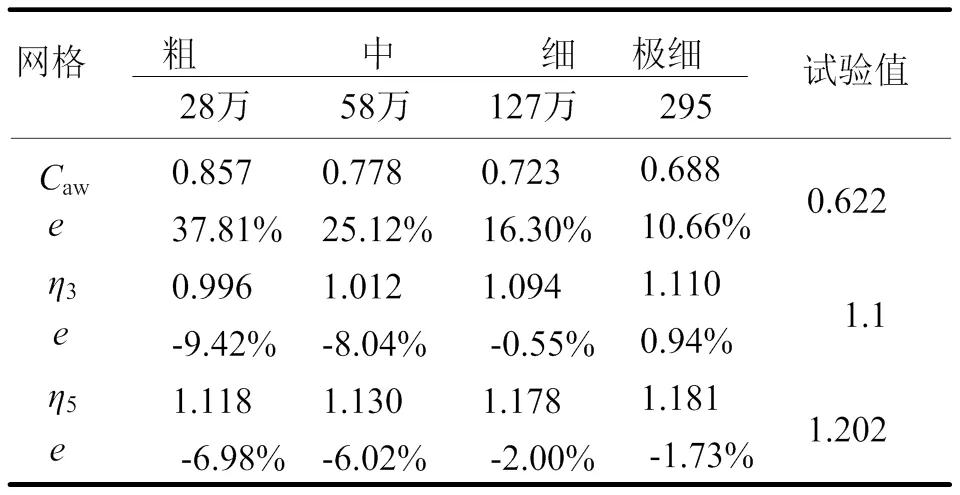
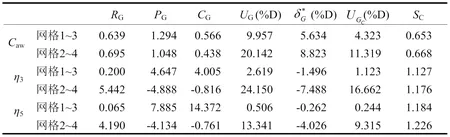
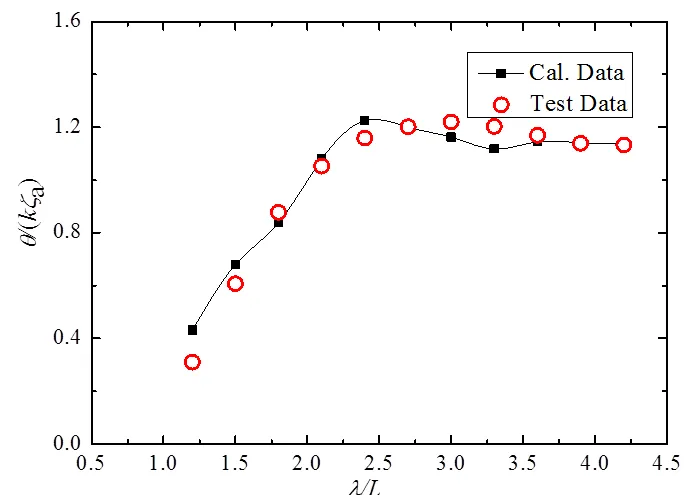
表2给出了静水中运动和阻力计算值的验证结果。表中下标G表示网格收敛性研究,G为收敛因子,计算结果单调收敛的条件为0 表1 静水中阻力与运动计算结果 4.1.2确认 表3给出了静水中运动和阻力计算值的确认结果,表中的确认不确定度。文中所用试验结果的实验不确定度D为2.5%。从表3中可以看出,阻力和纵倾的计算结果在修正和未修正的情况下均得到了确认。垂荡的相对误差较大,但绝对误差较小,其原因为垂荡值本身就较小,较小的相对误差就会对绝对误差造成较大影响。从阻力和纵倾来看,计算结果仍然是可靠的。 4.2 波浪中阻力增值与运动CFD不确定度分析 4.2.1 验证 4.2.1.1 网格收敛性研究 表2 静水中阻力与运动计算值的验证 表3 静水中阻力与运动计算值的确认 表4 波浪中阻力增值与运动计算结果 表5给出了波浪中阻力增值与运动计算值的验证结果。从表5中可以看出,波浪中计算结果的网格不确定度G明显大于静水,其原因为当网格加粗时,计算结果变化较大,采用该方法得到的计算结果仍然是可信的。垂荡和纵摇计算结果的精度阶数和收敛因子都较大,说明距离渐进区较远,在未修正时不确定度分析结果参考意义较大。另外,各修正结果的网格不确定度较未修正时均明显减小。 4.2.1.2 时间步长收敛性研究 表6给出了利用极细网格分别选取时间步长=e/320、e/240和e/180的数值模拟所得到的阻力增值与船体运动响应计算结果与试验值的对比。从表6中可以看出,随时间步长的减小,阻力增值、垂荡和纵摇计算结果均逐渐减小,向实验结果逼近,并在减小过程中跨越试验值。 表7给出了波浪中阻力增值与运动计算值时间不长收敛性的验证结果。表中下标T表示时间收敛性研究。从表7中可以看出,阻力增值、垂荡和纵摇计算结果均满足单调收敛条件,阻力增值计算结果的精度阶数和收敛因子都较大,说明阻力增值计算结果距离渐进区较远,在未修正时不确定度分析结果参考意义较大。 4.2.2确认 表8给出了波浪中阻力增值与运动计算值的确认结果,表中的确认不确定度。从表8中可以看出,阻力增值、垂荡和纵摇计算结果在修正和未修正的情况下均得到了确认。波浪中计算结果的不确定度大于静水,其原因为波浪中有更多的因素可能导致误差,如造波和消波、船体的的运动等。在未修正的情况下,计算结果的对比误差相对较小,其中垂荡和纵摇误差小于2%,但确认不确定度相对较大,阻力增值的确认不确定度在11%~21%之间,垂荡和纵摇网格2~4的确认不确定度分别大于20%和10%。较大确认不确定度来源于计算资源的限制,如网格数量、时间步长和计算时间等。从上文的分析来看,本文的数值计算方法仍然是可靠的。 4.3 船体运动分析 采用上文的计算方法,对该WPC的耐波性进行进一步预报,取3.2~11.2 m等11个波长,使用极细网格,选取时间步长为=e/430。计算得到的船体运动响应与试验结果的对比如图4和图5所示(F=0.73)。从图4和图5中可以看出,垂荡及纵摇运动响应的计算结果与试验结果总体规律一致,随着波长增加,船体运动响应先增大,达到峰值后逐渐减小。垂荡运动在/<2.0时计算值略低于试验值,在/≈2.2时垂荡运动响应出现峰值,比试验结果向短波方向偏移。纵摇运动响应在2.2 图4 垂荡运动响应曲线计算值与试验值的比较 表5 波浪中阻力增值与运动计算值的验证 表6 取不同时间步长时波浪中阻力增值与运动计算结果 4.4 阻力增值分析 阻力增值计算结果与试验结果的对比如图6所示。从图6中可以看出,阻力增值的数值计算结果与试验结果较为吻合,/<1.7及/3.3时计算值略低于试验值;共振区处的峰值误差小于5%,船体运动与阻力增值计算与实验结果的吻合也证明了本文计算方法的可靠性。 图5 纵摇运动响应曲线计算值与试验值的比较 本文采用RANS方程建立了穿浪双体船迎浪纵向运动响应和阻力增值数值计算方法,开展了垂荡、纵摇及阻力增值的不确定度分析和不同波长下的数值计算,得到如下结论。 1)对静水中的阻力及船体姿态及波浪中的阻力增值和船体运动分别进行了验证和确认,采用本文计算方法得到的结果均得到了确认。 2)随着波长增加,船体运动响应先增大,达到峰值后逐渐减小。各波长处船体运动及阻力增值的计算结果均与试验数据吻合较好,证明了本文建立计算方法的可靠性。 图6 阻力增值曲线计算值与试验值的比较 表7 波浪中阻力增值与运动计算值的时间步长收敛性验证 表8 波浪中阻力增值与运动计算值的确认 [1] Castiglione T, Stern F, Bova S, et al. Numerical investigation ofthe seakeeping behavior of a catamaran advancing in regular head waves[J]. Ocean Engineering, 2011, 38 (16): 1806–1822. [2] Carrica P M, Huiping F, Stern F. Computations of self-propulsion free to sink and trim and of motions in head waves of the KRISO container ship (KCS) model[J]. Applied Ocean Research, 2011, 33(4): 309-320. [3] Guo B J, Steen S, Deng GB. Sea-keeping Prediction of KVLCC2 in Head Waves with RANS[J]. Applied Ocean Research, 2012, 35:56-67. [4] Simonsen CD, Otzen J F, Joncquez S, et al. EFD and CFD for KCS heaving and pitching in regular headwaves[J]. Journal of Marine Science and Technology, 2013, 18: 435-359. [5] Hosseini H S,Wu P C, Carrica P M,et al. CFD verification and validation of added resistance and motions of KVLCC2 with fixed and free surge in short and long head waves[J].Ocean Engineering, 2012, 59: 240-273. [6] Qian P, Yi H, Li Y. Numerical and experimental studies on hydrodynamic performance of a small- water plane-area-twin-hull (SWATH) vehicle with inclined struts[J]. Ocean Engineering, 2015, 96: 181-191. [7] Tezdogan T, Demirel Y K, Kellett P, et al. Full Scale unsteady RANS CFD simulations of ship behaviour and performance in head seas due to slow steaming[J]. Ocean Engineering, 2015, 97: 186-206. [8] 吴乘胜, 陈雄, 孙立宪, 等.静水中自由船模拖曳CFD模拟方法研究[J].船舶力学, 2010, 14(8):823-833. [9] Wu Chengsheng, Chen Xiong, Sun Lixian, et al.Numerical simualtion of free ship model towed in still water[J]. Journal of Ship Mechanics, 2010, 14(8):823-833. Analysis on Uncertainty of CFD for Longitudinal Motion and Added Resistances of Wave Piercing Catamaran in Head Waves Zhao Shuai, Bai Weibin, Zhou Shuai, Liu Haoran, Zhou Lixue (Naval University of Engineering, Wuhan 430033, China) U661.32 A 1003-4862(2017)04-0061-06 2016-12-05 赵帅(1995-),男,在读大学生。专业方向:电气工程。E-mail: 314779878@qq.com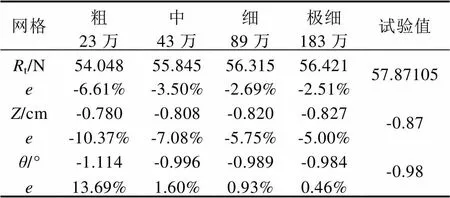

5 结论