基于时域微分的地铁直流供电系统故障定位仿真

金雪丰，李正茂，胡 振



基于时域微分的地铁直流供电系统故障定位仿真

金雪丰1,2，李正茂2，胡 振2

（1. 武汉船用电力推进装置研究所，武汉430064；2. 武汉长海电气科技开发有限公司，武汉 430200）

地铁运行过程中，金属性短路故障是最常见且最严重的故障类型之一，为了快速而准确地对地铁直流供电系统故障定位，提高城市轨道交通用直流牵引供电系统的工作可靠性，结合我国某地铁供电系统建立了直流供电系统短路故障电路拓扑结构模型。根据时域微分方程理论，计算了短路故障点与变电所的距离。运用最小二乘法对数据处理优化，提高了故障定位的准确性。研究结果表明：双端供电系统中，故障点位于两变电所中间区域时，定位准确度较高；短路点在两站中间位置的500 m范围内时，使用该方法定位误差小于6.15%。

直流供电系统 城市轨道交通 金属性短路故障 故障定位

0 引言

我国正大力发展城市轨道交通，用于解决国内日益拥堵的城市交通问题。地铁的迅速发展极大地方便了人们的出行，同时对供电系统的安全可靠运行提出了新的要求。为了加强地铁供电系统的可靠性，一方面通过研究新型的、分断性能更好的直流设备以适应地铁线路的不断增长和客运压力的增长，同时研究新的保护算法使保护装置动作可靠、灵敏；另一方面，研究一种能够快速定位故障点的装置，用于接触网故障精确定位，快速检修并排除故障，恢复供电系统的正常运行。

实际运行中城市轨道交通供电系统绝大多数故障是接触网故障，一旦接触网发生故障，将导致牵引供电的中断，影响城市轨道交通的正常运营[1]。直流牵引供电系统故障定位的研究是为了帮助检修员快速并准确的定位故障点，从而维护人员及时赶到现场对故障点进行抢修，及时恢复供电，保证供电系统的正常工作。

目前，国内地铁牵引供电系统中尚无成熟的故障定位装置投入实际应用，传统的方法耗费大量时间及人力，越来越不能满足地铁发展的需求。因此研究一种故障定位算法，快速、准确获取故障位置进而排除故障，保证地铁直流牵引供电系统的安全可靠运行，具有重要意义。

地铁牵引供电系统故障定位的研究主要参考电气化铁路中的故障定位方法以及高压直流输电系统故障定位方面的应用研究[2-4]。目前，地铁中最常用的故障测距算法主要借鉴已有的电力系统输电线路故障测距方法：故障分析法和行波法。故障分析法以阻抗法为主，测量误差较大；行波法虽然在直流输电系统的故障定位中得到广泛的应用，但是对于城市轨道交通直流供电系统供电而言，其供电距离短，一条1200 m的接触线发生近端短路时，传播到两端监测点的时间差仅为几十微秒，通信设备微小的误差以及延时就会导致较大的测距误差，对通信设备的要求高。同时在接触网或者第三轨参数没有完整获取时，行波法波速度无法确定，也会带来很大的误差，不利于故障的定位。

鉴于上述方法的优缺点，基于时域微分方程的故障定位法，在原理上不受非周期分量和各次谐波的影响，无需时域-频域转换，适用于从瞬时到稳态的故障全过程中任意一段数据，具有快速、简便和鲁棒性等特点，在工程应用方面具有研究价值[5]。基于时域微分方程理论，利用MATLB/ Simulink建立轨道交通供电系统模型，对地铁故障定位进行仿真分析。

1 基于时域微分方程的故障定位法原理

当地铁直流供电系统处于短路暂态过程中，对地铁直流牵引供电系统的故障暂态过程建立微分方程。由于该方法不受非周期分量和各次谐波的影响，故测量得到的电气量无需进行滤波处理。

1.1 典型直流牵引供电系统

地铁牵引供电系统主要由牵引变电所和牵引网组成，如图1所示。牵引变电所通过城市电网110 kV或者10 kV经降压、整流后，获得24脉波直流，经过进线柜到750 V/1500 V正母线，再经过馈线柜和上网柜至接触网或者接触轨向机车提供牵引动力，并经过钢轨（回流轨）、负母线、负极柜等回流至牵引变电所负极。

图1中所示为双边供电方式，当接触网发生短路故障时，短路电流来自于左右两侧牵引变电所。由于整流机组的外特性，导致非故障接触网上的电流也给短路点提供电流，因此，在故障分析时，需要考虑故障点两侧的牵引变电所、上下行接触网、以及整流机组的影响。

图1 直流牵引供电系统短路故障示意图

1.2 双端故障定位原理

当A、B供电区间内有一辆机车在距A站的距离占A、B之间线路长度的百分比为时，接触网与钢轨之间发生短路故障。根据图1中所示直流牵引供电系统短路故障，以及戴维南或诺顿定理建立等效电路模型，如图2所示。在戴维南等效电路中，牵引变电所用等效为内阻抗s、s与理想电压源s相串联。其中，理想电压源是牵引变电所直流母线的空载电压，该值主要由交流电源电压和整流电路拓扑结构决定；而等效内阻抗则由交流电源系统阻抗、整流元件的电压降、整流变压器阻抗以及整流电路的工作状态等决定[6]。

当左右两侧牵引变电所之间某处发生接地短路故障时，假设短路故障点与牵引变电所A之间的距离占A、B之间线路长度的百分比为。两侧牵引变电所的直流馈线电压分别为dA、dB，故障接触网两端电流分别为kz、ky，流过非故障接触网的电流为kc，短路点处过渡电阻为f，过渡电感为f，短路电流为f。接触网及走行轨采用集中式参数模型，接触网参数分别为c、c，走行轨参数分别为r、r。

根据基尔霍夫电流定理和基尔霍夫电压定理，图2的时域微分方程为：

(2)

由公式(1)减去公式(2)，整理后得：

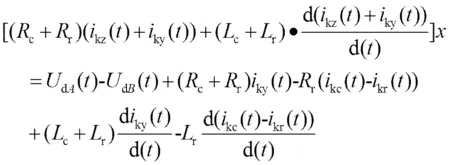
由于直流牵引供电系统中实际的馈线电压、馈线电流均为采样值，故此可以将微分方程(3)转换成差商方程，采用向后差商并整理后得：

(4)

式(4)为故障测距的差商方程，可以写成矩阵的形式=，其中，是m×m矩阵，是m×1矩阵，是m×1矩阵。故障定位方程为：-1。其中电压、电流采样值均已知，将采样值分别代入式(4)求解故障距离比例。由于每一采样时刻均能得到一个定位结果，故(=1,2,3…n)为一系列近似值，所以故障点与A站之间的距离(=1,2,3…n)为一系列近似值。为消除个别数据点不准确带来的测距误差，采用最小二乘法对测距方程(5）优化求解，获得故障点的位置。

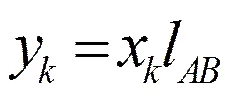
最小二乘法作为优化算法的目标函数为若干个函数的平方和，如式(6)所示，最小二乘法的目标就是寻求一个向量，使得目标函数在该向量处有最小值min(x)[7]。

(6)

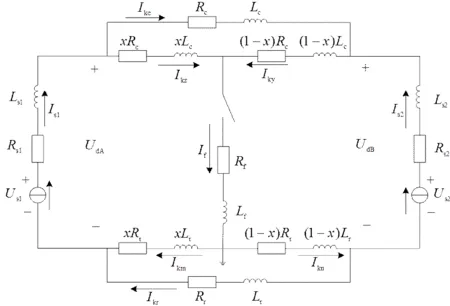
图2 牵引供电系统短路故障暂态模型

2 建模与仿真分析

根据地铁直流供电系统特性以及图2所示直流供电系统短路暂态模型，建立MATLAB/Simulink模型如图3所示。线路中参数分别为c=0.028 Ω/km，c=2.663e-3H，r=0.023 Ω/km，r=1.78e-3H，l=4 km；f=0.2e-3Ω。分别仿真了不同短路距离时的结果，如表1所示。

由表1可得，线路中短路点越趋近于两站中间时，计算误差越小，该故障定位法月准确。短路点在两站中间位置的500 m范围内时，可使用该方法。

3 误差分析

基于微分方程的双端故障定位算法优点是计算量小、所需参数值较少、数据窗短，适用于短路过程从暂态发展到稳态的任意一段数据且无需滤波。但双端测距法依赖于数据采集装置、时间同步装置、通讯技术装置等硬件，同步要求高、需要精确的牵引网参数。

基于双端数据的故障测距算法需使用故障区间两侧牵引变电所的数据，在代入测距方程进行计算时，需将双端数据严格对齐，但受现场设备及直流牵引供电系统负荷电流不断变化的特点的限制，双端数据很难对齐。

双端数据不同步的直观表现是，一端记录的短路发生时刻靠前，另一端记录的短路发生时刻靠后。

实际上，接触网及钢轨的阻抗参数在暂态过程中不断变化，对故障定位的准确度带来较大误差。

表1 短路点与A站不同距离时的仿真结果

4 结论

直流牵引供电系统中两变电所之间距离一般在1~5 km之间，对接触网与走行轨采用集中式参数模型，仿真结果证明该模型在故障测距时精度较高。

时域微分方程与最小二乘法相结合，对直流供电系统能够有效的故障定位。且在双端供电系统中，故障点越趋近于两变电所中间区域时，定位准确度越高。

虽然故障定位算法适用于短路暂态过程中的任意一段数据，为了降低数据不同步造成的误差，采用0.02 s至0.12 s的数据长度（短路时刻=0.02 s），有效的降低了因数据不对齐造成的误差。

双端供电系统中，该故障定位法在短路点越趋近两站中间，准确度越高。因此该故障定位法不适用于双端供电时近端短路工况。

双端供电系统中，故障定位计算时对采集装置的精度、数据同步要求较高，以及线路参数暂态变化是故障定位的主要误差来源。所以准确确定线路参数对测距误差的影响还需深入研究。

[1] 陈丹. 地铁牵引供电系统故障测距研究[D]. 西南交通大学, 2009.

[2] 宋国兵, 蔡新雷,高淑萍,等. 高压直流输电线路故障定位研究综述[J]. 电力系统保护与控制, 2012, 40(5): 133-137.

[3] 李强, 王银乐. 高压输电线路的故障测距方法[J]. 电力系统保护与控制, 2009, 37（23）: 192-197.

[4] 和敬涵, 孟鑫, 宋晓明. 基于时域微分的地铁直流牵引系统故障定位[J]. 电工技术学报, 2016, 31（3）.

[5] 全玉生, 李平, 张煌等. 基于微分方程的单端故障测距新算法[J]. 电网技术, 2004, 28(21): 47-50.

[6] 黄德胜,张巍. 地下铁道供电[M]. 北京: 中国电力出版社, 2010: 50-52.

[7] 张勋. DC1500V牵引供电系统故障测距研究[D]. 西南交通大学, 2011.

Simulation of Fault Location for Subway DC Power Supply System Based on Time Domain Differential

Jin Xuefeng1,2, Li Zhengmao2, Hu Zhen2

（1. Wuhan Institute of Marine Electric Propulsion, Wuhan 430064, China; 2. Wuhan Changhai Electric Technology Development Co., LTD, Wuhan 430200, China）

TM71

A

1003-4862（2017）04-0067-04

2016-11-01

金雪丰（1977-），男，工学硕士。研究方向：牵引供电系统、直流开关电器。

E-mail: jin_xuefeng79@qq.com