低轨四星时差定位技术研究

张义超,乔夏君,陆浩然,张镇琦

(北京宇航系统工程研究所，北京 100076)

低轨四星时差定位技术研究

张义超,乔夏君,陆浩然,张镇琦

(北京宇航系统工程研究所，北京 100076)

文章重点分析影响低轨四星时差定位系统精度的主要因素;首先，从四星时差定位的基本原理出发，对四星时差定位的模型和几何精度因子进行了详细的推导，并通过仿真分析了四星构型、时差测量精度、卫星位置误差、基线长度、星座投影面积等对四星时差定位系统精度的影响；通过比较可知，在相同参数条件下，采用Y形构形，减小时差测量误差、提高卫星定位精度、增加基线长度，增大星座投影面积均等均能够提高该系统的定位精度；在低轨四星定位系统应用场景中，四星构型、卫星绝对位置测量精度、基线长度以及星座投影面积对四星时差定位系统精度影响较大，时差测量精度和卫星相对位置测量精度对四星时差定位系统精度影响较小;而在实际任务中应权衡各因素的效费比，来保证定位精度。

低轨；四星；时差定位；几何精度因子

0 引言

在电子侦查领域中，精确的定位技术具有非常重要的意义[1]：在军事领域中，定位技术应用于精确打击武器，为最终摧毁敌方提供有力的信息保障。有源定位技术具有全天候、高精度等一些优点，但也容易暴露己方位置，从而遭受到敌方的软干扰或硬性武器的攻击。无源定位技术自身不发射信号，而是利用目标自身辐射信号或外辐射信号对目标进行定位，能够适应军事活动中对于隐蔽性的要求。

星载无源定位系统以卫星为平台，不受领土、领空、领海和天气条件的限制，可以对相对较大范围内的目标进行定位。一般来说，星载无源定位技术有单星测频 / 测向定位、双星时差联合定位、三星时差定位、四星时差定位和四星时差联合定位等[2-5]。其中，单星测频 / 测向、双星时频差、三星时差都需要通过地球方程约束对地面目标进行定位，或在已知高程信息的情况下对空中目标进行定位，而四星时差定位可以得到三个独立的时差值，无需额外信息即能对目标进行高精度的三维定位。本文主要给出基于四星时差定位的基本原理，通过仿真结果对影响四星时差定位的各个因素进行了对比分析。

1 四星时差定位基本原理

时差定位(TDOA，time difference of arrival)又称为双曲线定位，其原理是利用辐射源的信号到多个测量站的时间数据，从而对辐射源进行定位。四星时差定位的原理是通过测量地面辐射源的信号到达主星和副星的时间差，从而计算辐射源的位置[6]。设S0为主星，S1、S2、S3为副星，若在每颗卫星上安装上侦察接收机，地面上的辐射源发出的电磁波信号被 4部接收机接收，测量信号到达每颗卫星的时间，可得到3个独立时差方程：

(1)

式中,td0,td1,td2,td3分别为同步测量的信号到达卫星接收机的时间；d0,d1,d2,d3分别为辐射源到卫星的直线距离；c为光速。每一个时差方程确定一个以主星和副星为焦点的单叶双曲面，3个单叶双曲面相交于一点，该点的位置就是辐射源的位置。

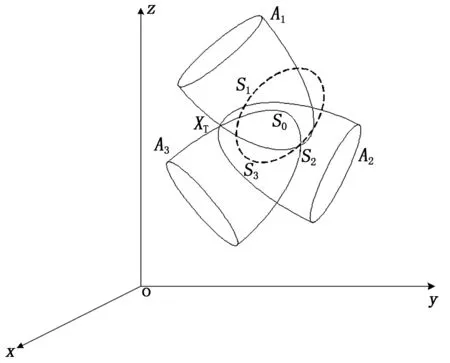
图1 四星时差定位原理

2 四星时差定位精度模型

为描述定位误差与几何位置的关系，定义了定位精度的几何稀度GDOP(geometric dilution of precision)[7]，它用于描述定位误差的三维几何分布，通常用下式表示，即：

(2)

式中，σx,σy,σz分别表示x,y,z方向上的定位标准差。

假定三维时差定位系统的示意图如图2所示，该系统由一个主星和3 个副星构成，其中假定S0为主星，S1、S2、S3为副星，待求解的目标辐射源的三维位置为pT。

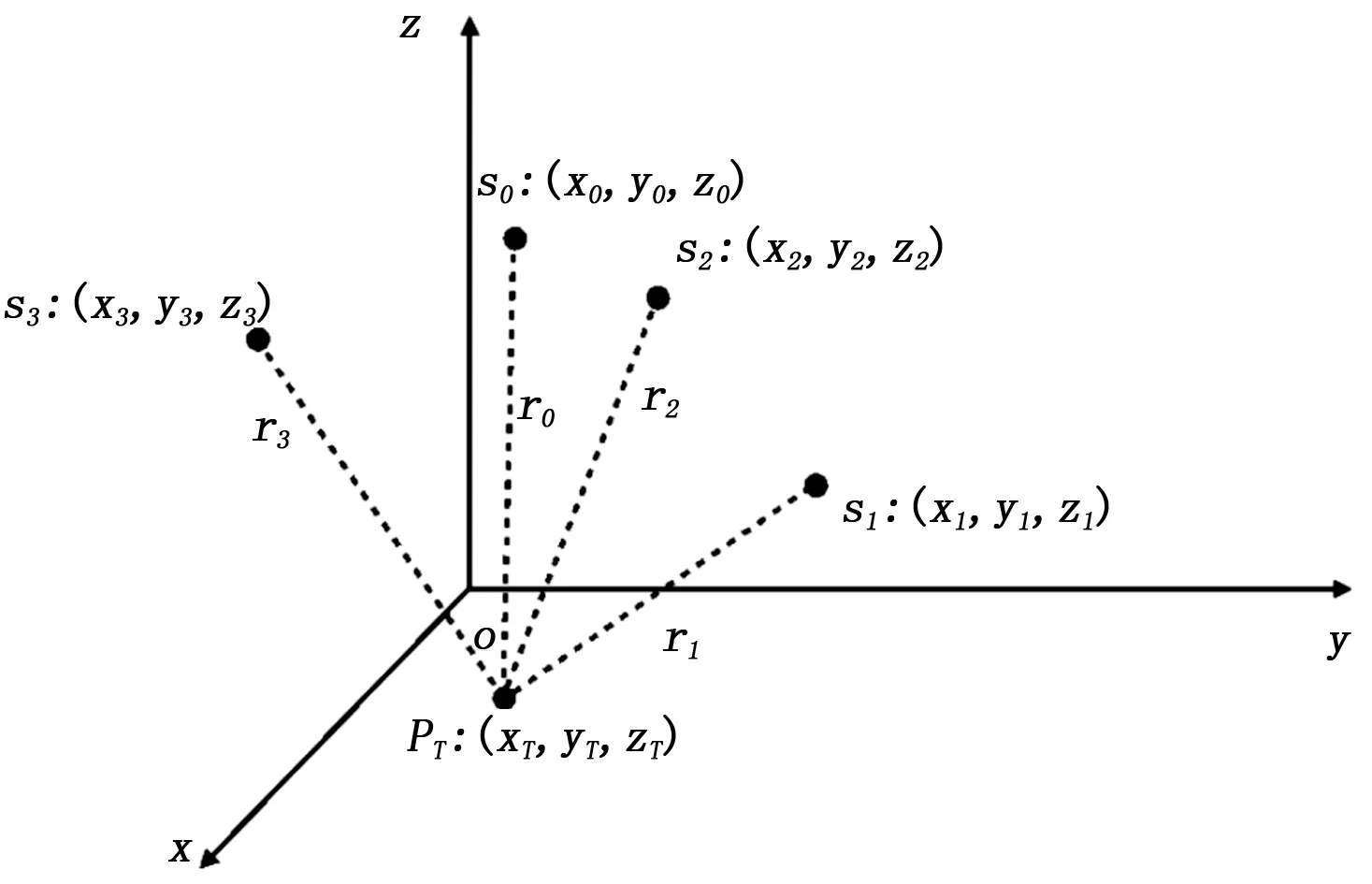
图2 时差定位几何示意图

由各个卫星的位置信息、目标辐射源的位置信息及辐射源与各星之间的距离，可得:

(3)

其中:c表示光速；ri表示各星同目标辐射源之间的径向距离；Δri表示目标辐射源与第i颗副星之间的径向距离和其与主星之间径向距离的差值。对距离差Δri求微分，可得:

C·dX=dY-U0ds0+U1ds1+U2ds2+U3ds3

(4)

其中:

令B=(CTC)-1·CT。由于主星在测量辐射源信号到达时间时存在误差，且该误差存在于每个时差量中，所以每个Δri的测量误差都是相关的。假设通过系统修正之后，测量误差的均值为零，而且卫星位置误差每个元素之间以及各卫星位置误差之间不相关，则目标辐射源定位误差的协方差矩阵为:

(5)

式中,

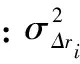
目标辐射源的位置误差协方差矩阵为:

(6)

依据GDOP的定义就能够获得三维空间时差系统定位的几何精度。

(7)

3 四星时差定位精度分析

3.1 影响定位精度的因素

采用四星时差定位技术开展无源电子侦察应用，影响定位精度的因素有四星构型、时差测量精度、卫星定位精度、基线长度、星座投影面积几个因素决定[8]，下面主要以低轨四星定位为应用场景分析各因素对定位精度的影响。

3.2 四星构型

卫星轨道高度200km，基线长度为60km，时差测量精度50ns，卫星绝对位置测量精度150m，卫星相对位置测量精度50m，四星采用不同的构形(Y形，T形，菱形)，进行仿真，以主星星下点为圆心建立直角坐标系，得到GDOP分布如图3所示。

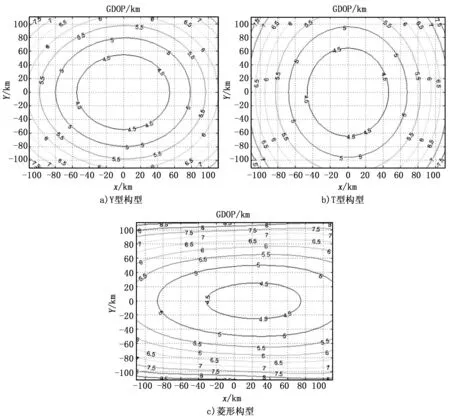
图3 不同构型GDOP分布

由上图可知，在相同参数条件下，Y构形分布在星下点半径58km范围内能达到4.5km定位精度，且分布均匀；T构形定位精度高，但分布略有不均，菱形构形定位精度和分布情况均最差。

3.3 时差测量精度

卫星轨道高度200km，基线长度为60km，采用Y形构形，频差测量精度10Hz，速度测量精度1m/s，卫星绝对位置测量精度150m，卫星相对位置测量精度50m，现取星下点100km圆周上的一个点，使时差测量精度取值0～200ns，仿真得到GDOP与时差测量精度的关系曲线如图4所示。

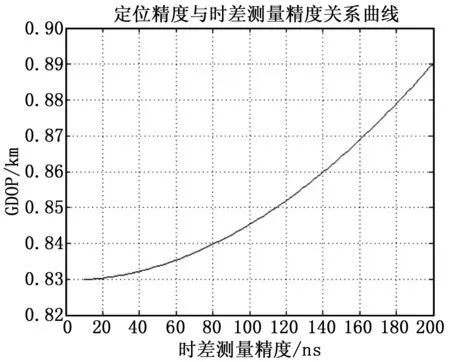
图4 GDOP随时差精度变化曲线

由上图可知，时差测量精度越高，四星定位精度越高。但时差测量精度对定位精度的影响较小。

3.4 卫星定位精度

3.4.1 绝对位置测量精度

卫星轨道高度200km，基线长度为60km，采用Y形构形，时差测量精度50ns，频差测量精度10Hz，速度测量精度1m/s，卫星相对位置测量精度50m，现取星下点100km圆周上的一个点，使绝对位置测量精度取值50～300m，仿真得到GDOP与绝对位置测量精度的关系曲线如图5所示。

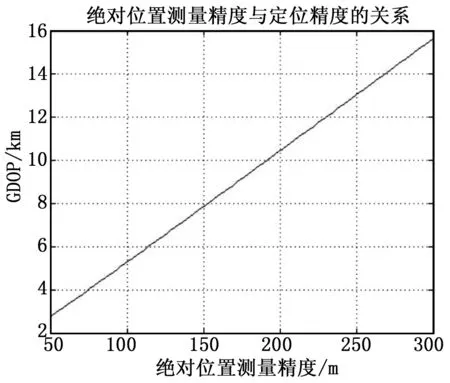
图5 GDOP随绝对位置测量精度变化曲线

3.4.2 相对位置测量精度

卫星轨道高度200km，基线长度为60km，采用Y形构形，时差测量精度50ns，频差测量精度10Hz，速度测量精度1m/s，卫星绝对位置测量精度150m，现取星下点100km圆周上的一个点，使相对位置测量精度取值20～60m，仿真得到GDOP与相对位置测量精度的关系曲线如图6所示。

图6 GDOP随相对位置测量精度变化曲线

3.4.3 小结

由图分析得出，定位精度随绝对位置测量精度和相对位置测量精度的提高而提高，其中与绝对位置测量精度近乎呈线性关系，但是当相对位置测量精度从20m变为160m时，定位精度仅下降600m，故相对位置测量精度对GDOP的影响较小。

3.5 基线长度

卫星轨道高度200km，采用Y形构形，时差测量精度50ns，频差测量精度10Hz，速度测量精度1m/s，卫星绝对位置测量精度150m，卫星相对位置测量精度50m，现取星下点100km圆周上的一个点，使基线长度取值20km～120km，仿真得到GDOP与基线长度的关系曲线如图7所示。

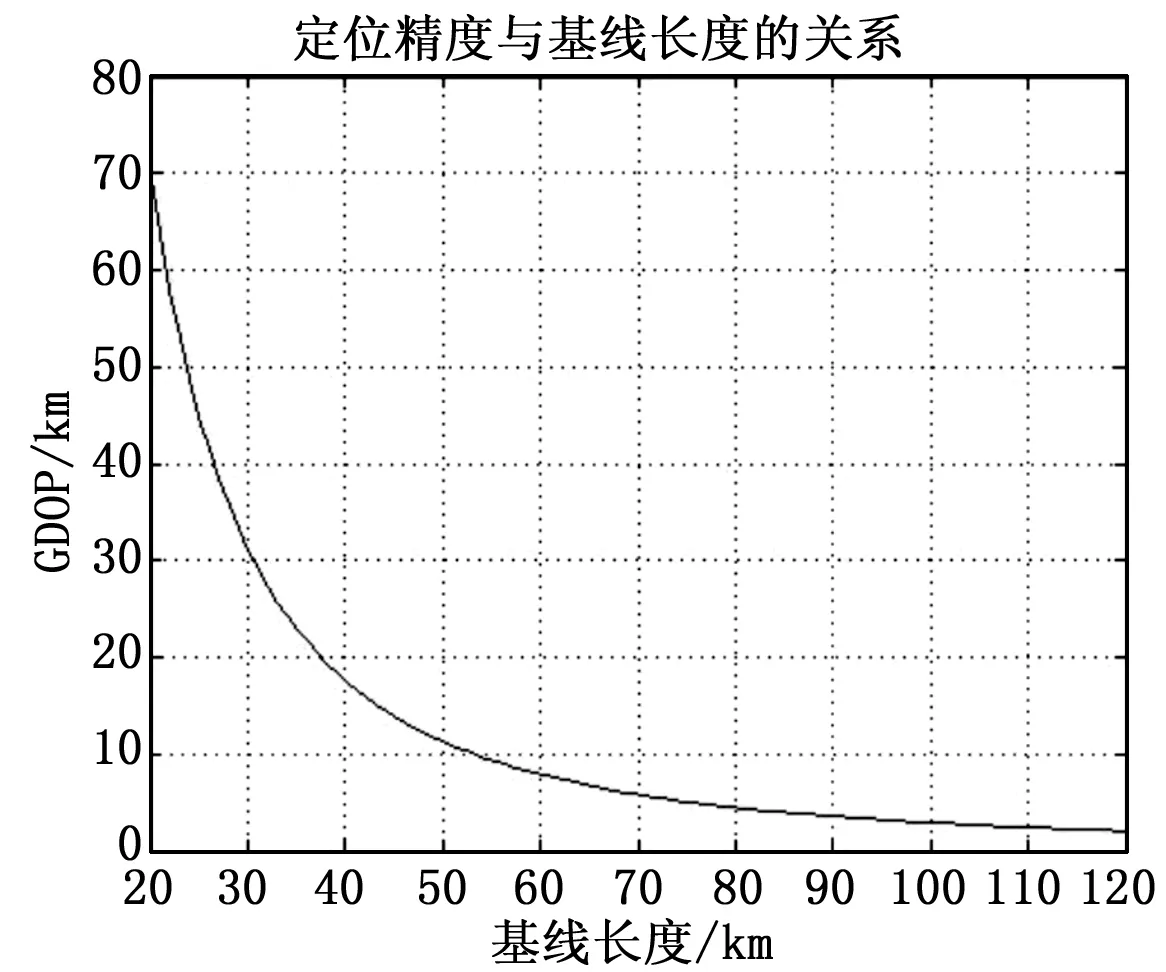
图7 GDOP随相对基线长度变化曲线

通过对基线长度因素的仿真分析，可得到结论：随着基线长度的增加，定位精度呈指数形式提高。

3.6 星座投影面积

卫星轨道高度200km，基线长度为60km，采用Y形构形，时差测量精度50ns，频差测量精度10Hz，速度测量精度1m/s，卫星绝对位置测量精度150m，卫星相对位置测量精度50m，现取星下点100km圆周上的一个点，分析其GDOP与星座投影面积的关系如图8所示。

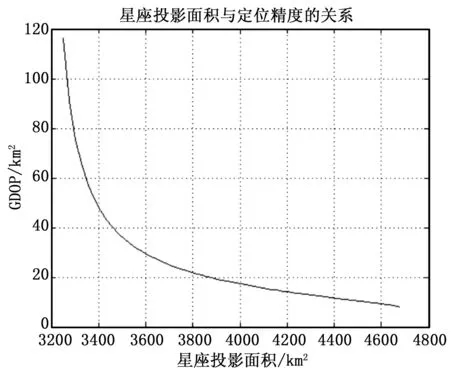
图8 GDOP随星座投影面积变化曲线

星座投影面积与定位精度有近乎指数增加的关系，随着星座投影面积的增大，定位精度将得到大幅提高。当卫星面与地球表面平行时，能达到最大定位精度。

4 结论

本文主要介绍了四星时差定位的基本原理，并从理论角度推导了基于四星时差定位的GDOP精度模型。针对低轨四星定位应用场景，通过仿真、对比分析了6个影响四星时差定位系统精度的因素。仿真结果表明四星构型、卫星绝对位置测量精度、基线长度和星座投影面积对四星时差定位精度影响较大，时差测量精度和卫星相对位置测量精度对定位精度影响精度较小。而在实际任务中应权衡各因素的效费比，来保证定位精度。

[1]WilsonJ.PrecisionLocationandIdentification:aRevolutioninThreatWaringandSituationalAwareness[J].JournalofElectronicDefense,1999,22(11)：43-48.

[2] 黄 振，陆建华. 天基无源定位与现代小卫星技术[J]. 装备指挥技术学院学报，2003，14(3)：24-29.

[3] 朱冯喆.多星时差频差定位技术研究[D].南京：南京理工大学，2009.

[4] 陆安南.对电子侦察卫星无源定位技术发展问题的思考[J].通信对抗，2008 (1):15-20.

[5] 杜亚平.星载定位体制及误差分析研究[D].成都：电子科技大学，2009.

[6] 李建军.四星时差定位算法研究[J]. 电子对抗技术，2004,19(4): 3-6.

[7] 张 勇，盛卫东，郭福成，等.低轨双星无源定位算法及定位精度分析[J].中国惯性技术学报, 2007,15(2):188-192.

Research of Location Technology on TODA with Four LEO Satellites

Zhang Yichao，Qiao Xiajun，Lu Haoran, Zhang Zhenqi

(Beijing Institute of Astronautical Systems Engineering，Beijing 100076，China)

This paper mainly discusses the factors which decides the localization accuracy of TDOA with LEO four satellites. Firstly, we derive the TDOA localization model and GDOP of LEO four satellite based on the principle of TDOA. Secondly, some simulation results about factors including locations of four satellites, the accuracy of TDOA measurements, geometry of four satellites, the length of baseline, the projection area of four satellites, are demonstrated. By comparison, it is seen that one can improve the accuracy of localization by decreasing TDOA measuring errors and base station errors, increasing the length of baseline and area of projection area when using the Y geometry of four satellites. For LEO satellite application, geometry, the precision of absolute locations of four satellites,the length of baseline affect the accuracy of localization importantly, while TDOA measurement error, the precision of relative locations of four satellites effects the localization accuracy of our system minor. Therefore, we should choose these factors based on the trade-off of their accuracies and obtaining costs.

LEO; four-satellite TDOA; GDOP

2016-10-26；

2017-01-05。

张义超(1986-)，男，河北省唐山市人，硕士研究生，主要从事空间电子信息系统方向的研究。

1671-4598(2017)05-0165-04DOI：10.16526/j.cnki.11-4762/tp

VP

A