虚拟阵列Khatri-Rao积与子空间联合稀疏表示的DOA估计方法

朱进勇，王立冬，孟亚峰

(军械工程学院 电子与光学工程系，石家庄 050003)

虚拟阵列Khatri-Rao积与子空间联合稀疏表示的DOA估计方法

朱进勇，王立冬，孟亚峰

(军械工程学院 电子与光学工程系，石家庄 050003)

利用目标信号在空域分布的稀疏性，该文提出了一种基于虚拟阵列Khatri-Rao(KR)积与信号子空间联合稀疏表示的单快拍DOA估计方法；该方法利用单次快拍的采样数据，构造出双向虚拟阵列数据，并对虚拟阵列数据的协方差矩阵进行KR积变换处理，然后对向量化后的数据进行顺序重构，利用重构矩阵的大奇异值对应的左奇异向量为估计信号子空间；最后，利用凸优化工具箱对稀疏模型进行二阶凸规划的优化求解，得到高精度的DOA估计值；仿真实验验证了算法的有效性，在低信噪比下比传统MUSIC和OMP算法具有更高的估计精度。

虚拟阵列；Khatri-Rao积；稀疏表示；单快拍；波达方向估计

0 引言

波达方向角(direction of arrival, DOA)估计[1-2]作为阵列信号处理领域研究的热点内容，被广泛应用于无线通信、测速、雷达、地质勘探等众多领域。但传统MUSIC算法和ESPRIT算法为代表的子空间类算法对空域存在的相关信源进行DOA估计时便失效。近年来，压缩感知理论的兴起，使得DOA估计有了质的飞跃性发展，与传统的子空间类算法不同，稀疏重构类DOA估计算法利用目标信号在空域的稀疏特性，可以高概率重构原始信号，从而不考虑子空间维数和秩的亏损问题[3-5]。

基于稀疏分解的DOA估计算法不需要关注目标信号的统计特性、是否相关以及在较小的快拍数下就能得到较好的估计精度和分辨精度，因此，国内外学者提出了很多基于稀疏分解的DOA 估计方法。文献[6]提出了L1SVD算法，采用奇异值分解降低算法复杂度和噪声的敏感性，结合凸优化进行稀疏重构目标，解决了压缩感知在理论在DOA 估计上的基本问题，但是该方法运算量较大；文献[7]提出了Khatri-Rao子空间分解方法，这种方法能够处理N≤2M-2个目标信源个数的情况，但该方法是建立在信源的数目N为已知条件的情况下才能准确的分离出信号子空间和噪声子空间；文献[8]提出了基于KR积变换和空域平滑理论的DOA 估计算法，利用空域平滑处理，使协方差恢复满秩，减少了运算量；文献[9]提出了基于信号子空间的迭代加权最小方差算法，利用奇异值分解得到低维的接收信号矩阵，采用迭代加权最小方差求解欠定的稀疏表示问题，能对任意相关信号进行处理，但是该方法需要已知信源个数；文献[10]提出了对多快拍接收信号的协方差矩阵进行l1 2混合范数联合稀疏表示，但由于需要对协方差矩阵求逆，因此在快拍数较少的情况下，导致算法的性能急剧下降。

本文提出一种建立在KR积理论变换的基础上，将虚拟阵列技术和信号子空间相结合进行联合稀疏表示的DOA 估计方法。该方法利用阵列接收信号的单次快拍数据，进行双向虚拟平移处理，以达到处理相干信号的目的；在此基础上，利用KR积变换理论对虚拟平移的数据矩阵进行处理，得到向量化空间矩阵；然后利用奇异值分解向量化空间矩阵提取信号子空间，得到低维的信号子空间，再采用二阶锥规划求解的方法以及结合l1范数凸优化[11]问题进行DOA求解。该方法从信号的本质上解决了相干问题，减少了运算量。通过仿真实验证明了本文算法在低信噪比情况下，比传统的MUSIC算法和压缩感知DOA 估计算法具有更高的估计精度。

1 信号模型

假设M个各向同性阵元组成的等距均匀线阵(Uniform linear array, ULA)，阵元间距为d=λ/2，λ为信号波长。空域存在N个远场窄带信号s1(t)，s2(t),…,sN(t),分别以方位角θ1,θ2,…，θN入射到ULA。阵列的接收信号可写为:

X(t)=A(θ)S(t)+N(t)

(1)

式中，X(t)=[x1(t),x2(t),…,xM(t)]T为阵列天线接收矢量，A(θ)=[α(θ1),α(θ2),…,α(θN)]为M×N维的阵列流行矩阵，其中，α(θi)=[1,e-j2πdsinθ1/λ,…,e-j2π(i-1)dsinθi/λ]T,1≤i≤N为目标信源入射角θi的导向矢量，N(t)为M×1维的阵列接收噪声矩阵。

2 本文算法

2.1 双向虚拟阵列

根据虚拟阵列技术，每次将M个阵元向右平移d，形成一个虚拟子阵，如此反复M-1次，与真实的天线阵列接收数据形成一个方阵接收数据。对于第p次右相平移得到的阵列输出信号表示为:

Xp(t)=ADrp-1S(t)+Np(t)

(2)

式中，Drp-1为N×N的对角阵的p-1次乘方，平移矩阵Dr表示为:

Dr=diag(e-j2πdsinθ1/λ,…,e-j2πdsinθN/λ)

(3)

利用M-1次的阵列虚拟数据构造如下接收阵列信号矩阵:

[X(t),X1(t),…,X(M-1)(t)]T

(4)

那么:

Xr=X(t)[1,Dr,…,Dr(M-1)]T

(5)

因此，获得阵列虚拟处理后的协方差矩阵为:

(6)

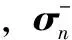
同理，左向虚拟阵列的协方差矩阵为:

Rl=E[XlXlH]=

(7)

式中，C2=[1,Dl,…，Dl(M-1)]T，Dl=diag(ej2πdsinθ1/λ,…,ej2πdsinθN/λ)。

2.2 协方差矩阵的KR积处理

假设矩阵A=[α1,α2,…,αF]∈CI×F和B=[b1,b2,…,bF]∈CJ×F，定义两个矩阵的Khatri-Rao积[12]为:

A×B=[a1⊗b1,a2⊗b2,…，aF⊗bF]∈CIJ×F

(8)

式中，“×”和“⊗”分别为KR积与Kronecker积的运算符号。

假设ai=[ai1,ai2,…,aiI]T∈CI，bi=[bi1,bi2,…，biI]T∈CI(i=1,2,…,F)，因此Kronecker积表示为:

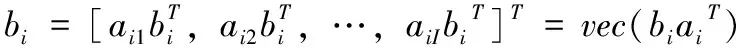
(9)

因此，根据KR积变换理论，对式(6)和式(7)进行向量化运算可以得到:

(10)

(11)

式中，“vec”表示矩阵的向量化处理，Γr=AC1和Γl=AC2为旋转阵列流行矩阵。

利用左右虚拟阵列协方差的向量化形式，构造出左右虚拟阵列的稀疏重构观测向量：

(12)

(13)

(14)

YSV=AXSV+NSV

(15)

通过SVD分解将M×M维的数据变成了M×N维，不仅降低了数据的维数还保持了观测矩阵的稀疏性和稀疏结构，并不影响DOA估计。

根据压缩感知理论中的信号恢复理论，可以容易的得到目标函数为:

(16)

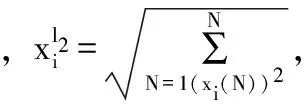
1)获取阵列观测的单次快拍数据X(t)，分别进行左右平移构造出虚拟子阵Xr和Xl；

2)对虚拟子阵Xr和Xl进行协方差处理，得到协方差矩阵Rr和Rl；

3)利用KR积理论对Rr和Rl进行向量化运算，并求得平均稀疏观测向量y；

4)对观测向量进行顺序重构得到M×M的方阵Y；

6)利用凸优化工具箱求解优化函数。

3 算法性能分析

从以上的推导过程可以看出，本文算法在l1-SVE算法的基础上运用虚拟阵列技术和KR积变换理论对信号进行联合稀疏表示。该算法的的计算量主要集中在凸优化工具箱进行二阶锥规划问题的求解，因此与l1-SVD算法的复杂度O(N3P3)相差无几，P为整个空域平均分的份数。

本文算法通过双向虚拟阵列技术将单快拍的接收数据构成方阵的协方差矩阵恢复到满秩，使该文算法具有了相关信号的处理能力。需要注意的是，本文算法只采用了一次的快拍数据，在进行SVD分解估计信号子空间的过程中得不到多次快拍中信号的能量累积，所以并不能有效的估计DOA。

4 仿真实验与分析

4.1 算法的估计特性比较

实验中采用8个阵元的ULA，阵元间距为半波长，两个远场窄带不相关的信源分别以θ1=20°和θ2=40°的方位角入射到ULA。本文算法采用的快拍数K1=1，l1-SVD，OMP和MUSIC算法采用的快拍数K2=50。将空域的-90°～90°范围以1°的等间隔划分为181份来构造过完备阵列流行矩阵，图1为空间谱图。

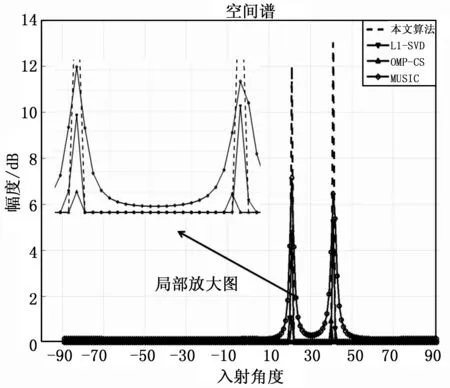
图1 空间谱

4个远场窄带信源分别以θ3=-50°，θ4=-10°，θ5=20°和θ6=70°的方位角入射到ULA，其中θ3和θ4为相干信源，θ5和θ6为不相关信源，其空间谱图如图2所示。

图2 相关信源空间谱

由图1和图2可知，本文算法对相关信号和不相关信号均能进行有效的DOA估计，传统的MUSIC算法未能对相关信号进行DOA估计，l1-SVD和OMP能完成对相关信号的DOA估计。本文算法通过虚拟阵列技术将接收信号的协方差恢复到了满秩，有了更强的解相干信号的能力，在后期的信号恢复上是由于基于压缩感知理论的DOA估计算法是将空域的目标信号的DOA估计当作一个稀疏向量的重构恢复问题，这与MUSIC算法的子空间分解类思想是完全不同的。

4.2 算法的统计特性比较

在不同的信噪比下，本文算法与，OMP和MUSIC算法对信号角度估计的均方根误差值(Root Mean Square Error, RMSE)。实验中采用两个窄带远场信号θ1=20°和θ2=40°，信噪比变化范围为-10～30 dB，仿真结果为50次Monte-Carlo统计结果，其它条件与实验一相同。这里定义角度估计的均方根误差为:

(17)

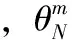
由图3可知，在低SNR时，本文算法，l1-SVD和OMP算法的RMSE远高于传统的MUSIC算法，同时，本文算法的RMSE也小于l1-SVD和OMP算法的RMSE；随着SNR的增大，四种算法的RMSE均减小。

由图4可知，随着ULA阵元数的增加，可以提高本文算法的DOA估计精度。

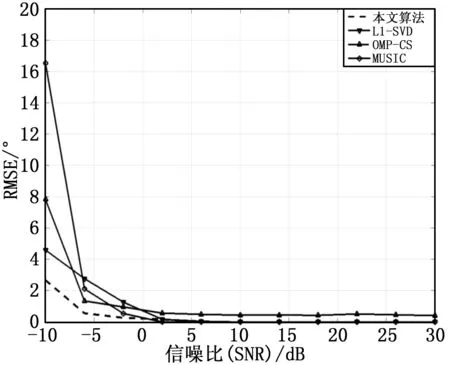
图3 DOA估计的RMSE

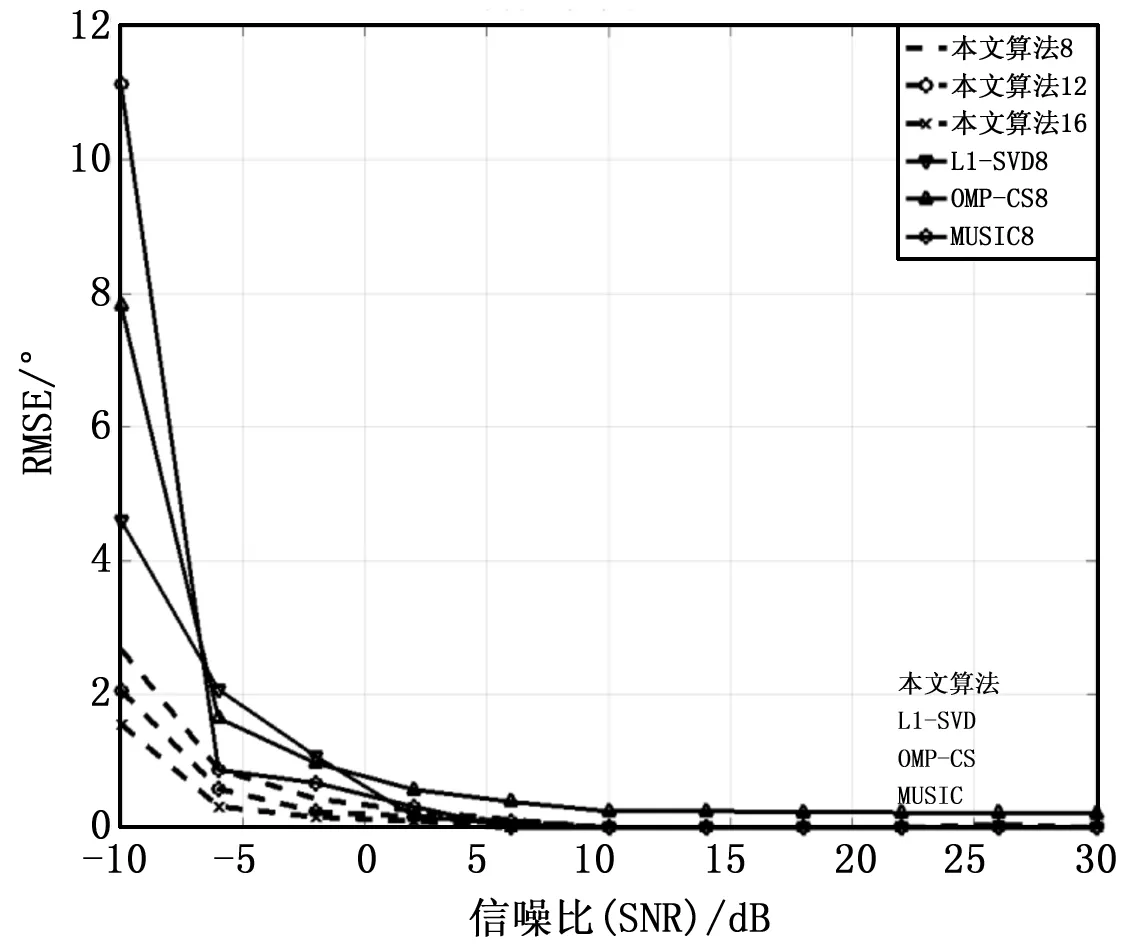
图4 阵元变化下的DOA估计的RMSE

4.3 成功概率比较

为研究本文算法对信号的估计成功概率，两个窄带远场信号θ1=20°和θ2=40°，仿真结果为50次Monte-Carlo统计结果，当DOA估计结果在[19.8°,20.2°]和[39.8°,40.2°]的区间时，认定一次成功，成功概率随SNR的变化情况如图5所示

可以看出在相同的SNR下，本文算法的DOA估计成功概率高于其它三种算法，在SNR≥9dB时，就能够实现100%的估计成功概率，而OMP算法具有最差的DOA估计成功概率，这从空间谱图也能看出；这是由于OMP算法在进行观测矩阵选择时具有比等距约束性(restrictedisometryproperty,RIP)条件[13]更加严格的要求，这就需要确定的迭代次数和更多的观测值，即使是这样也不能保证把任何信号都能够精确的重构出来；l1-SVD算法采用直接对待恢复信号进行l1范数约束，这将导致在恢复信号的过程中得不到更稀疏的结果，进而在DOA估计的空间谱上出现伪谱峰，降低了DOA的估计精度。

图5 DOA估计成功概率

5 结束语

本文在KR积变换理论的基础上，提出了一种在单快拍条件下对顺序重构虚拟阵列的提取信号子空间稀疏表示的DOA估计算法，经过仿真验证本文算法对相关信号具有更强的处理能力，尤其是在低信噪比情况下相对于l1-SVD，OMP和MUSIC算法估计精度也大大提高。然而，本文算法利用凸优化工具箱处理，在运算量方面并没有太大的优势，这方面还需要更进一步的研究。

[1] GRANT M and BOYD S. CVX: Matlab software for disciplined convex programming[OL].http://cvxr.com/cvx,2012.

[2] 王 凌，李国林，刘坚强，等.一种基于数据矩阵重构的相干信源二维测向新方法[J].西安电子科技大学学报，2013，40(2):130-137.

[3] 杜新鹏.联合稀疏恢复新型算法及其应用研究[D].长沙：国防科技大学,2013.

[4] 刘庆华，欧阳缮，何振清.准平稳信号的Khatri-Rao积联合稀疏分解DOA估计方法[J].系统工程与电子技术，2012,34(9):1753-1757.

[5] 严金山，彭秀艳，王咸鹏.基于酉变换的虚拟阵列DOA估计算法[J].哈尔滨工业大学学报，2012,44(4):136-140.

[6] Malioutov D, Mujdat C, Willsky A. A sparse signal reconstruction perspective for source localization with sensor arrays[J].IEEE Transaction on Signal Processing,2005,53(8):3010-3022.

[7] Ma W K, Hsieh T H, Chi C Y. DOA estimation of quasi-stationary signals with less sensors than sources and unknown spatial noise covariance: A Khatri-Rao subspace approach[J].IEEE Transaction. On Signal Processing, 2010,58(4):2168-2180.

[8] 蔡晶晶，宗 汝，蔡 辉.基于空域平滑稀疏重构的DOA估计算法[J].电子与信息学报,2016,38(1):168-173.

[9] 解 虎，冯大政，魏倩茹.采用信号子空间稀疏表示的DOA估计方法[J].系统工程与电子技术，2015,37(8):1717-1722.

[10] Yin J H, Chen T Q. Direction-of-arrival estimation using a sparse representation of array covariance vectors[J].IEEE Transaction. on Signal Processing letter, 2011,59(9):4489-4493.

[11] Tibshirani R. Regression shrinkage and selection via the LASSO[J].Journal of the Royal Statistical Society: Series B,1996,58(1):267-288.

[12] Ma W K, Hsieh T H, Chi C Y. DOA estimation of quasi-stationary signals with less sensors than sources and unknown spatial noise covariance: A Khatri-Rao subspace approach[J].IEEE Trans. On signal Processing, 2010,58(4):2168-2180.

[13] Candes E J, Tao T. Decoding by linear programming[J]. IEEE Transactions on Information Theory,2005,51(12):4203-4215.

Virtual Array Khatri-Rao Product and Subspace Joint Sparse Representation Method of DOA Estimation

Zhu Jinyong, Wang Lidong, Meng Yafeng

(Department of Electronic and Optical Engineering, Ordnance Engineering College, Shijiazhuang 050003,China)

Using the target signal in the spatial distribution of sparse, this paper puts forward a Khatri-Rao(KR) product based on virtual array and signal subspace joint sparse representation of single snapshot DOA estimation method. The method uses a single snapshot sampling data, constructs the two-way virtual array data, and the covariance matrix of the virtual array data for KR product transformation process, and then to reconstruct the order of data after vectorization, by using the large singular values of reconstruction matrix left singular vectors of the corresponding to estimate the signal subspace; Finally, using convex optimization toolbox for sparse matrix model of quadratic convex programming optimization solution, get high accuracy DOA estimate. Simulation experiments verify the effectiveness of the algorithm, under the low SNR has higher estimation accuracy than traditional MUSIC,SVD and OMP algorithm.

virtual array; Khatri-Rao product; sparse representation; single snapshot; DOA

2016-10-11；

2016-12-20。

国家自然科学基金资助项目(61372039)。

朱进勇(1992-)，男，硕士研究生，主要从事信息与通信方向的研究。

1671-4598(2017)05-0147-03

10.16526/j.cnki.11-4762/tp.2017.05.041

TN911.7

A