基于时空模式的轨迹数据聚类算法

石陆魁，张延茹，张 欣

(1.河北工业大学 计算机科学与软件学院,天津 300401; 2.河北省大数据计算重点实验室(河北工业大学),天津 300401) (*通信作者电子邮箱shilukui@scse.hebut.edu.cn)

基于时空模式的轨迹数据聚类算法

石陆魁1,2*，张延茹1，张 欣1

(1.河北工业大学 计算机科学与软件学院,天津 300401; 2.河北省大数据计算重点实验室(河北工业大学),天津 300401) (*通信作者电子邮箱shilukui@scse.hebut.edu.cn)

针对轨迹聚类算法在相似性度量中多以空间特征为度量标准，缺少对时间特征的度量，提出了一种基于时空模式的轨迹数据聚类算法。该算法以划分再聚类框架为基础，首先利用曲线边缘检测方法提取轨迹特征点；然后根据轨迹特征点对轨迹进行子轨迹段划分；最后根据子轨迹段间时空相似性，采用基于密度的聚类算法进行聚类。实验结果表明，使用所提算法提取的轨迹特征点在保证特征点具有较好简约性的前提下较为准确地描述了轨迹结构，同时基于时空特征的相似性度量因同时兼顾了轨迹的空间与时间特征，得到了更好的聚类结果。

时空模式；轨迹数据；曲线边缘检测；相似性度量；密度聚类

0 引言

近年来随着移动定位服务和云计算技术的发展，搜集和处理移动定位信息已成为现实。由移动定位数据组成的海量数据库推动了关于移动定位数据研究的发展。作为典型的移动定位数据之一，时空轨迹数据是指沿时间顺序对空间移动对象的数值型记录，包括采样点位置、采样时间、速度等，而空间对象的这些特征都有可能随着时间的推移而发生变化，人们尝试着将这些可感而不可知的感性知识转化为有现实意义的数字信息，用于生活，提供便利。然而面对规模庞大的时空轨迹数据，如何快速地从中挖掘有用价值是人们必须面对的一个重要问题。

为了从时空轨迹数据中获取有用信息，聚类技术被用于对空间移动对象时空特征的提取。目前研究重点主要集中在轨迹数据模型定义、相似性度量和轨迹聚类方法三个方面。文献[1]基于全区间模型对轨迹进行聚类，提出一种基于采样和密度的轨迹聚类算法，使用轨迹全体采样点来度量整条轨迹的相似性，并采用基于密度的聚类算法完成聚类。文献[2]根据已有时空轨迹数据样本提取轨迹线索特征并进行汇总，以线索相似性来衡量两条轨迹之间的距离。然而将轨迹作为整体进行聚类的方法可能会忽略存在于整体相似度低的轨迹之间的局部相似性。文献[3]提出了一种划分-归组(Partition-and-Group)聚类框架，该方法首先使用最小描述长度 (Minimum Description Length, MDL)对轨迹进行子轨迹段划分，然后使用基于密度的聚类方法(Density-Based Spatial Clustering of Applications with Noise, DBSCAN)对划分后的子轨迹段进行聚类。其中MDL方法产生于对某种模型进行编码压缩的要求，其原理是计算出总描述长度最小的模型，应用到轨迹划分中时，可能会导致轨迹划分不具有实际代表性，失去其现实意义。文献[4]首先根据相邻轨迹样本点的转向角对轨迹进行划分，其次通过计算轨迹段的结构(方向、速度、转角、位置)相似度来判断轨迹的匹配程度，进而完成轨迹聚类。该提取特征点的方法适用于相邻样本点角度变化较明显的如道路轨迹数据中,然而在相邻样本点持续局部小角度变化过程中形成整体大角度变化的情况下，该判断特征点的方法可能会导致移动轨迹的划分失去其准确性。

时空轨迹数由位置坐标和相应的时间标记合成，因此，时间特征对分析移动物体的运行模式非常关键。然而现有轨迹聚类算法中常常忽略了对时间特征的相似性度量，如文献[1-4]，为此，本文提出基于时空模式的轨迹数据聚类方法，以划分-归组聚类框架为基础，从轨迹特征点提取、时空相似性度量和轨迹聚类算法三个方面进行改进。首先为解决MDL或“相邻样本点转角”方法提取轨迹特征点有所不足的问题，借鉴图像曲线边缘信息检测的方法提取轨迹特征点，生成具有代表性的子轨迹段集合；其次采用DBSCAN算法同时根据空间和时间相似性对子轨迹段进行聚类，并使用搜索网格提高计算效率。

1 轨迹特征点的提取

1.1 相关定义

时空轨迹数据记录了持续移动对象在某时刻出现在相应位置上的一系列信息，是其运动状态下时空属性的表现。参考文献[3]对时空轨迹数据的定义进行扩展，在这里给出时空轨迹数据集、特征点集合以及子轨迹集合的数学定义。

定义1 时空轨迹数据集。给定时空轨迹数据集TRS，共有tranum条轨迹，表示为TRS={TR1,TR2,…,TRtranum}，集合中的每条轨迹都由若干个多维样本点组成，任意一条轨迹TRi表示为：TRi={P1,P2,…，Pitnum}，其中1≤i≤tranum，itnum为第i条时空轨迹样本点总数。轨迹中任意一个样本点Pj表示为Pj=〈pnum,ptraid,px,py,ptime〉，显示出在ptime时刻，轨迹ptraid中样本点pnum的位置为(px,py)，其中1≤j≤itnum。

定义2 特征点集合。对第i条轨迹进行子轨迹段划分，得到能够代表该条轨迹的特征点集合CHA_TRi，表示为CHA_TRi={tc1,tc2,…,tcicnum}，其中icnum为第i条轨迹特征点总数，集合中tci为该条轨迹的特征点，tci定义如样本点。

定义3 子轨迹段集合。根据所有轨迹的特征点集合生成全部轨迹的子轨迹段集合，假设共有lnum条子轨迹段，子轨迹段集合定义为SUB_TRS={L1,L2,…,Lk,…,Llnum}，其中Lk=〈tck,tck+1〉(1≤k≤lnum)，tck,tck+1为相邻特征点。

1.2 轨迹上特征点的判定

特征点定义为轨迹中行为变化相对明显的点，能很好地对轨迹结构进行描述，同时应具有一定简缩性及准确性。图像算法中通过检测曲线凹凸分界点来提取曲线边缘信息的方法可以应用到轨迹特征点的提取中。曲线的凹凸分界点指改变曲线向上或向下方向的点。过曲线上任意一点x可以作一条关于该条曲线的切线L，切线的方向与曲线上x点的方向相同，此时切线L在切点x附近的部分“最接近”曲线，由于曲线是其所有切线的包络线，因此在较小范围内，曲线上的点都处于切线L的同一侧。假设给定曲线是由彼此很接近的点集组成，曲线的切线可以由曲线上彼此紧挨着的两个点构成的正向直线代替。据此，推广到轨迹应用中，假设某条轨迹上存在着两个相邻样本点x和x′，且这两个样本点之间的距离非常近，利用无限逼近思想，过这两点可以作一条关于该条轨迹的切线，通过判断样本点与该点相邻轨迹段(即切线)的变化趋势来确定该点是否为特征点。相关定义[5]如下：

定义4 设平面上两点的坐标分别为P1(x1,y1)和P2(x2,y2)，x1≠x2，连接P1,P2点得到一条有向直线，称这条有向直线为正向直线，而对应的直线方程:

F:(y2-y1)(x-x1)+(x2-x1)(y-y1)=0

(1)

为关于P1,P2的正向直线方程F。

定义5 假设平面上存在一条正向直线L，根据L将平面上的点分为两类，处于正向直线L顺时针一侧的点称为关于L的内点，而处于正向直线L逆时针一侧的点称为关于L的外点。

定理1 记平面上两点P1,P2的正向直线方程F12的左端表达式记为：

F12(x,y)=(y2-y1)(x-x1)+(x2-x1)(y-y1)

(2)

对于不在直线L上任一点P0(x0,y0)，则有：

1)若F12(x0,y0)<0，则点P0是关于正向直线L的内点；

2)若F12(x0,y0)>0，则点P0是关于正向直线L的外点。

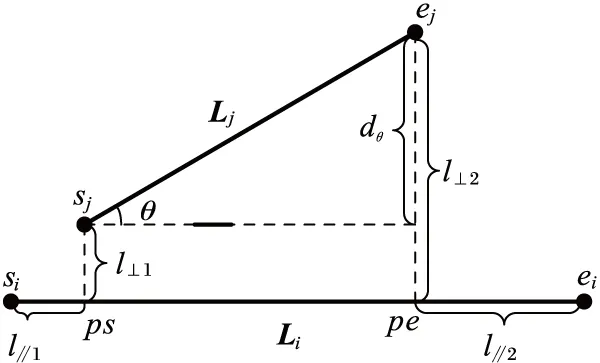
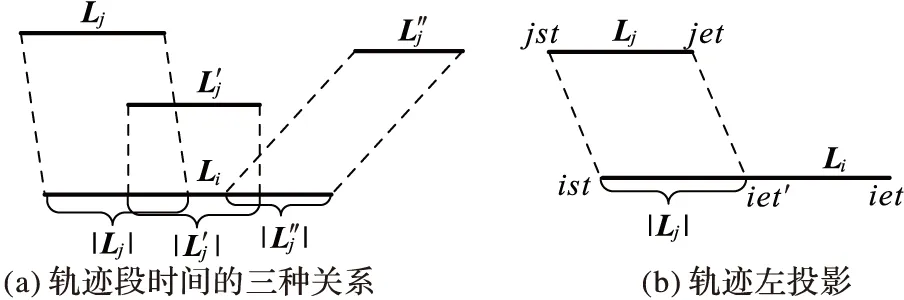
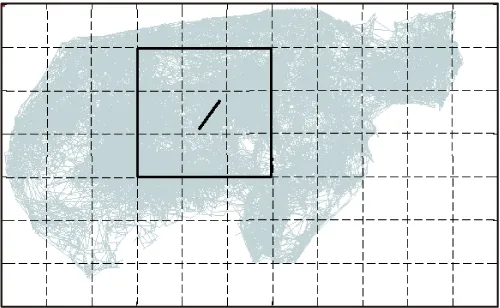
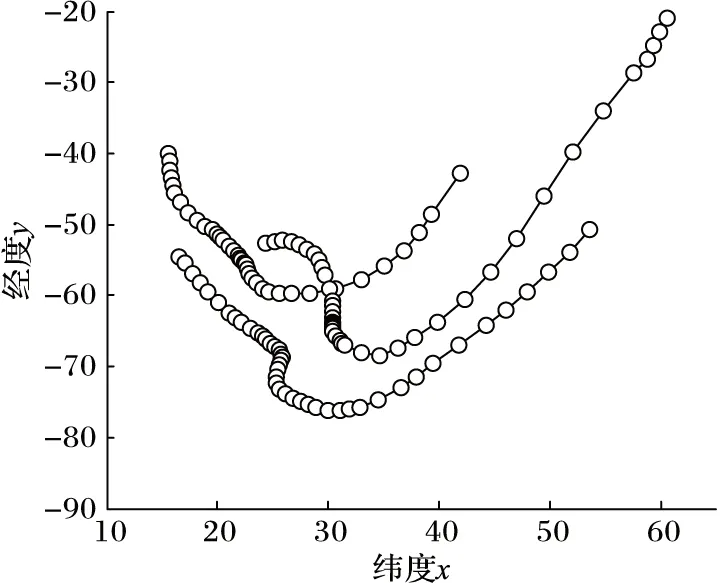
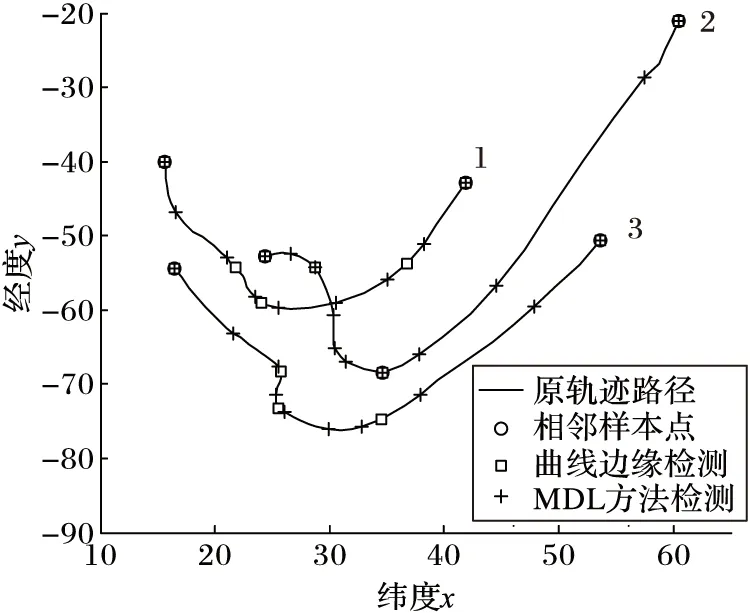
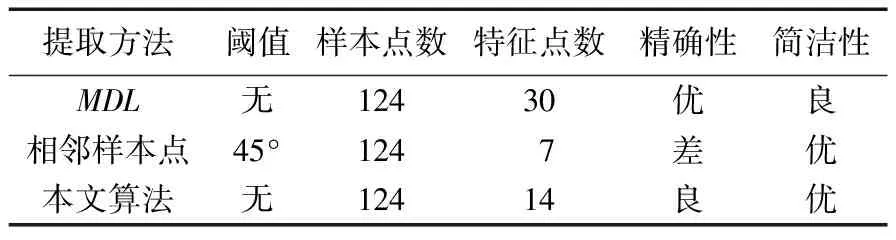
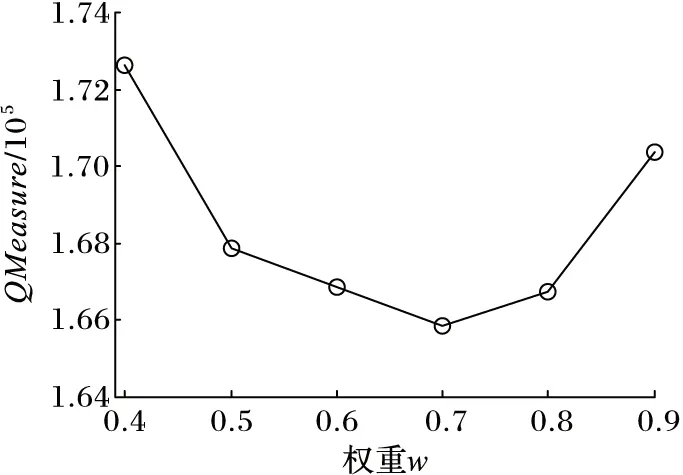
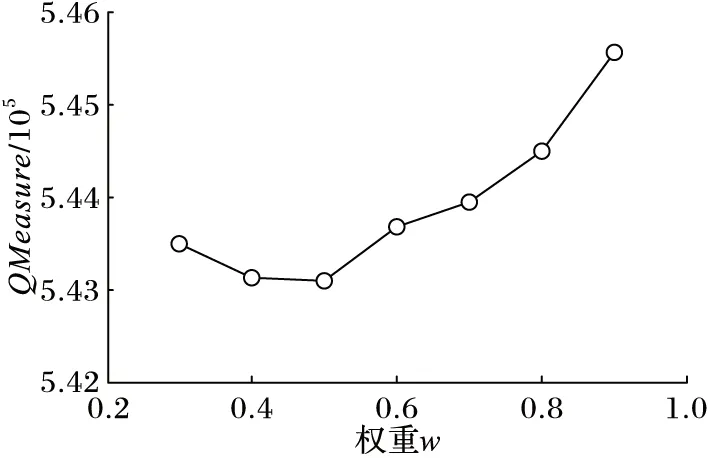
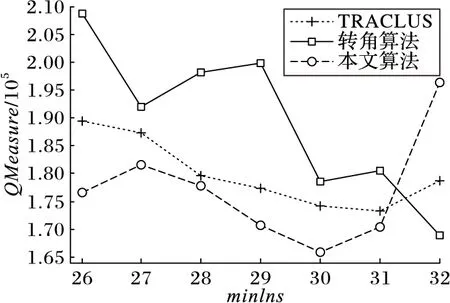
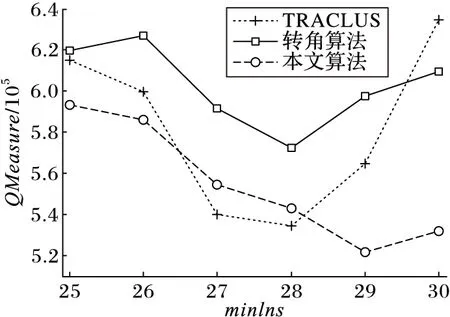
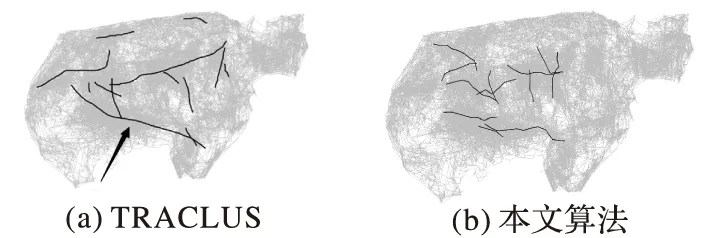
定理2 设P1(x1,y1)，P2(x2,y2)，P3(x3,y3)，P4(x4,y4)(x1

1)连接P1(x1,y1)，P2(x2,y2)点得到正向直线L1的方程为F12(x,y)=0，计算F12(x3，y3)的值；

2)连接P2(x2,y2)，P3(x3,y3)点得到正向直线L2的方程为F23(x,y)=0，计算F23(x4,y4)的值；

3)若F12(x3,y3)*F23(x4,y4)<0，说明在P3(x3,y3)点处轨迹的方向有所改变，认为P3(x3,y3)点是特征点，否则P3(x3,y3)不是特征点。

据此得到轨迹特征点提取方法，即由样本起点P1P2构成一条关于轨迹的切线L1，求P3点关于这条切线的内点或外点；由P2P3点构成另外一条关于轨迹的切线L2，求P4点关于这条切线的内点或外点；若P3和P4关于各自相邻切线发生变化，即P3P4不同为内点或不同为外点，那么认为P3点是轨迹在P1P2P3P4处发生变化的点，并添加到特征点集合中。循环判断，直到最后一个样本点。

伪代码如下所示。其中步骤1先将轨迹开始的点P1和P2添加到特征点集合中，从第三个点开始判断是否为轨迹特征点，如步骤2到步骤6所示，满足条件的轨迹点将被添加到特征点集合中，不满足条件将依次循环判断下一样本点直到轨迹结束点。步骤7将轨迹结束点添加到特征点集合中，至此完成特征点提取。步骤8至步骤17为轨迹特征点识别方法Calculate_cp()来判断current点是否为特征点，并返回逻辑值。最终利用生成的特征点集合形成该条轨迹的子轨迹段集合。

算法1CharacteristicPointsExtraction。

输入：一条轨迹集合TRi=P1P2…Pitnum

输出：该条轨迹特征点集合CHA_TRi={tc1,tc2,…,tcicnum}

步骤1 将P1P2点加入到集合CHA_TRi中；first=P1；

步骤2start=first;current:=start.next.next；

步骤3 while(current.next不为空)，转至步骤8调用方法Calculate_cp计算current是否为特征点；

步骤4 若current是特征点，将current点加入到特征点集合CHA_TRi中，否则不添加；

步骤5start=start.next;current=current.next；

步骤6 循环判断结束；

步骤7 将轨迹结束点添加到集合CHA_TRi中。

步骤8 初始化cpflag=false；

步骤9x1:=start.x;y1:=start.y；

步骤10x2:=start.next.x;y2:=start.next.y；

步骤11x3:=current.x;y3:=current.y;

步骤12x4:=current.next.x;y4:=current.next.y；

步骤13s1:=(x2-x1)*(y3-y1)+(y1-y2)*

(x3-x1)；

步骤14s2=(x3-x2)*(y4-y2)+(y2-y3)*

(x4-x2)；

主要考察了政府会计制度的改革以及国家会计制度改革对事业单位现有财务管理的影响，旨在促进未来治理制度和公共财务管理的某些改革。发现我国公用事业会计系统存在的一些问题，如会计核算和登记等系统管理不够规范，制度内容不健全等。在现行的会计和预算管理系统中，原有财务系统并不能反映该机构的实际情况。制度核算体制改革至关重要，会计制度改革是一项长期任务。目前，事业单位会计制度改革后，可以更有效地改善事业单位会计制度，大大提高事业单位的经济管理和资产管理，同时提高事业单位的办事效率。

步骤15s3=(x4-x2)*(y3-y2)+(y2-y4)*

(x3-x2)；

步骤16 if((s1*s2)<=0)cpflag:=true；

步骤17 returncpflag；

2 轨迹聚类算法

2.1 时空相似性度量

基于时空模式的轨迹聚类顾名思义就是要在时间和空间两种模式下对轨迹数据进行聚类，无论忽略哪一种属性，其聚类结果的准确性及现实意义都将大打折扣，那么针对目前大多数轨迹聚类算法着重考虑轨迹空间特征相似性度量忽略时间特征相似性度量的问题，本文提出一种兼顾时间与空间属性相似性的相似性度量方法，即在空间距离的基础上增加时间相似性距离判断。

时空模式下轨迹的空间相似性度量使用模式识别中常用的空间距离度量方法[3,6]，包括平行距离、垂直距离和角度距离。假设两条轨迹段分别为Li(si,ei)以及Lj(sj,ej)，其中si、ei、sj、ej分别表示Li和Lj的开始及结束点，并且Li≥Lj，由短轨迹段Lj两端点sj、ej向长轨迹段Li两端点si,ei垂直投影，得到Lj在轨迹段Li上的垂直点ps和pe，如图1所示。

图1 两轨迹段空间距离示意图

定义6 垂直距离。Li和Lj之间的垂直距离定义如下：

(3)

定义7 平行距离。Li和Lj之间的平行距离定义如下：

d//(Li,Lj)=MIN(l//1,l//2)

(4)

定义8 角度距离。Li和Lj之间的角度距离定义如下(其中‖Lj‖为Lj的长度)：

(5)

综上，Li与Lj之间的空间距离定义如下：

DS=d⊥(Li,Lj)+d//(Li,Lj)+dθ(Li,Lj)

(6)

计算轨迹段之间时间距离时，度量单位将是影响聚类分析结果的重要因素。诸多文献都使用标准分数z_score对数据进行预处理，以消除数据间存在着的单位差异[7-8]。其中文献[8]提出一种不等长时间序列(Short Time Series, STS)滑窗距离聚类算法，该算法使用z_score对时间序列进行标准化预处理，并设计基于滑窗的不等长时间序列距离计算方法，即设计长度等于较短时间段的滑动窗口，从较长时间段开始点向结束点滑动，得到一系列长度等于短时间序列的子序列集合，选择子序列中距离较短时间序列最近的STS距离作为这两条不等长时间序列的时间距离。然而通过实验证明，该方法具有较高的时间复杂度，计算花费非常大。

本文使用一种简单方法对时间数据进行预处理。首先以格林威治标准时间1987-12-31T00:00:00为时间起始点，此时设时间为1，以秒为单位依此类推，即1987-12-31T00:00:01设为2，最终时间范围为168 825 628～272 245 926。其次鉴于数值较大计算不便，本文时间数值除以一天秒数(86 400)对时间进行标准化设置，即时间/86 400所得值为最终标准化线性时间序列。应用到轨迹时间序列中，假设较长轨迹的时间段为Li(ist,iet)，ist和iet分别对应Li的开始时间和结束时间，较短轨迹的时间段为Lj(jst,jet)，其中jst和jet分别对应Lj的开始时间和结束时间，‖Li‖≥‖Lj‖。比较两条轨迹的时间段，可得三种情况：Li完全包含Lj，Li部分包含Lj以及Li完全不包含Lj，三种情况如图2(a)所示，其中‖Lj‖、‖Lj′‖、‖Lj″‖分别表示其长度。

应用到实际情况中，可能存在两条轨迹段时间跨度相差较大的情况，在这里取两条轨迹段之间的最近距离作为两条轨迹段的时间距离。将较短的子轨迹时间段Lj向较长的子轨迹时间段Li投影，以左投影为例，如图2(b)所示，将较短时间段结束点jet投影至较长时间段上距离其开始点ist长度为|Lj|的点，即iet′点，其中|iet′-ist|=|Lj|。据此将Li与Lj之间的时间距离定义如下：

(7)

图2 两条轨迹段时间距离

考虑到空间距离和时间距离存在着不同数量级的问题，在此使用z-score标准分数对空间及时间距离进行标准化。对变量f的度量值进行如下标准化[9]。

1)计算绝对偏差的平均值：

(8)

其中：x1f,x2f,…,xnf为f的n个度量值，mf为f的均值:

(9)

2)计算标准度量值：

Zif=(xif-mf)/sf

(10)

Zif为标准化后度量值，表示原始数据偏离平均值的程度,且服从正态分布。设标准化后空间距离和时间距离分别为DS′、DT′，通过设置距离权重w(0≤w≤1)，可以用来调整对空间距离和时间距离的敏感度，那么轨迹段间时空距离定义为：

DST=w×DS′+(1-w)×DT′

(11)

2.2 时空轨迹聚类算法

通过观察轨迹分段得到的子轨迹段集，可以发现子轨迹段形状具有不规则性，且集合中含有大量的噪声。由于DBSCAN算法通过对区域密度的连通性分析来聚类，不仅可以发现任意形状的聚类簇，而且在聚类过程中能够最大限度地避免噪声的干扰，因此在此采用该方法对子轨迹段进行聚类。该算法需要设定两个全局参数，即邻域半径eps和minlns。DBSCAN通过筛选子轨迹数据集中每个对象的eps邻域来搜索簇，如果对象p的eps邻域中包含的对象个数大于等于minlns个，则创建一个以p为核心对象的簇。然后，算法迭代地聚类从这些核心对象直接密度可达的所有对象，这个过程中可能涉及一些密度可达簇的合并，当没有新的对象添加到任何簇时，过程结束。下面给出相关定义[10]。

定义9eps邻域。以给定对象p为中心，半径为eps的区域称为该对象的eps邻域。

定义10 核心对象。在给定对象p的eps邻域内，如果样本点数大于等于minlns，则称该对象为核心对象。

定义11 直接密度可达。若给定对象q为核心对象，并且对象p在核心对象q的eps邻域内，那么称对象p从对象q出发是直接密度可达。

定义12 密度可达。样本集合D中，如果存在一个对象链p1，p2，…，pn，设p1=q，pn=p，若对象链中任意pi+1是从pi出发关于eps和minlns直接密度可达的，那么对象p是从对象q出发关于eps和minlns密度可达。

定义13 密度相连。如果样本集合D中存在对象o，使得对象p和q都是从o出发关于eps和minlns密度可达，那么称对象p和o是从对象q出发关于eps和minlns密度相连。

应用到轨迹段聚类中，需要扫描整个轨迹段数据集，找到任意一个核心轨迹段，对该核心轨迹段进行扩充。扩充的方法是寻找从该核心轨迹段出发的所有密度相连的轨迹段。遍历该核心轨迹段的eps邻域内的所有核心轨迹段，寻找与这些轨迹段密度相连的对象，直到没有可以扩充的轨迹段为止。之后重新扫描数据集(不包括之前寻找到的簇中的任何轨迹段)，寻找没有被聚类的核心轨迹段，再重复上面的步骤，对该核心轨迹段进行扩充直到数据集中没有新的核心轨迹段为止。数据集中没有包含在任何簇中的轨迹段可以认为是噪声点。算法时间复杂度的限制主要体现在邻域的计算，在不使用索引的情况下邻域计算需要遍历所有轨迹段，时间复杂度为O(n2),导致计算效率低；使用索引能够降低时间复杂度，如文献[3-4]都使用R-tree结构进行索引来提高整体计算速度，而Gudmundsson[11]近期提出利用并行算法来计算子轨迹集群的方法，以改进现有串行方法为基础，利用结合了GPU计算能力的并行技术来实现算法速度的大幅提高。由于其实现代价比较昂贵，在这里提出另外一种方法来降低时间复杂度。参考文献[12]设计交通路网的思想，本文首先根据数据样本集定义m*n的网格空间，并将每一格空间进行序号标记，统计每条轨迹穿过的所有网格。计算某条子轨迹段邻域的时候先以该条轨迹段所在网格为中心，向四周扩展，形成3×3的九宫格搜索区域，最终只需判断所有穿过该九宫格区域的轨迹，示意图如图3所示。

图3 数据索引搜索图

由此，本文提出一种改进的轨迹聚类算法，伪代码如下：

算法2TrajectorySegmentsClustering(TSC)。

输入：轨迹段集合TS={L1,L2,…,Llnum},邻域半径eps,最小轨迹段数minlns。

输出：聚类结果集合C={C1,C2,…,Cclusnum}。

步骤1 初始化clusterId=0,并将轨迹集合中所有轨迹段初始化为unclassified。

步骤2 循环判断集合TS中所有轨迹段，若轨迹段Li的标识为unclassified则执行步骤3。

步骤3 根据eps计算Li的邻域Nε(Li)。

步骤4 若|Nε(Li)|≥minlns，则为Li所有邻域轨迹段Nε(Li)分配为当前clusterId，并将Nε(Li)-{Li}添加到待扩展序列Q中，执行步骤8对序列Q进行可达近邻扩展；否则将此Li设置为noise。

步骤5clusterId++；将此Li设置为classified。

步骤6 循环判断结束。

步骤7 根据clusterId，输出聚类结果集合C={C1,C2,…,Cclusnum}。

步骤8 while(Q不为空)，选择Q中任意Qi。

步骤9 根据eps计算Qi的邻域Nε(Qi)。

步骤10 若Nε(Qi)≥minlns,执行步骤11；否则将Qi从序列Q中移除。

步骤11 对每一个X(其中X∈Nε(Qi))，若X为noise,将当前clusterId分配给X；否则将X添加至序列Q中。

步骤12 循环判断，直到Q为空。

3 实验结果

为测试所提算法的有效性，使用两个真实数据集进行测试：一是Starky收集的动物迁徙数据集(http://www.fs.fed.us/pnw/starkey/data/tables/)，提取该数据集1993年麋鹿的运动轨迹(简称Elk93)，并从传感定位数据源中提取经纬度坐标以及定位时间信息参与实验分析；Elk93由47 204个采样点构成33条轨迹。二是大西洋飓风数据(http://weather.unisys.com/hurricane/atlantic/)，选取经度纬度、采样时间属性参与实验；实验中选取1950—2009年之间的数据，经整理数据集由19 750个采样点组成639条轨迹。

为直观体现在轨迹提取特征点阶段所提方法的合理性，实验中选取1950年大西洋飓风数据中的三条轨迹进行测试(共124个样本点)，如图4所示，图中空心圆为样本点，整条轨迹由彼此紧挨着的相邻样本点构成。

图4 三条飓风轨迹数据

在实验中，使用三种提取特征点的方法进行实验比较，分别为文献[3]提出的一种近似MDL方法和文献[4]提出的利用相邻样本点转角角度变化来提取特征点的方法(其中转角阈值设置为45°)，以及本文提出的利用曲线边缘检测提取特征点的方法，提取结果如图5所示。以拥有32个样本点的2号轨迹为例，MDL算法提取了11个特征点(+标注)，简缩率约65%，而“转角”方法提取3个特征点(□标注)，简缩率90.6%，曲线边缘检测法提取特征点4个，简缩率约87.5%。

图5 三种特征点提取方法比较结果

三种特征点提取方法比较结果如表1所示。三条轨迹共有124个样本点，使用MDL方法提取特征点数为30个，在精确性方面表现良好，但在简缩性方面有些不足；由于轨迹相邻样本点转角变化不大导致根据转角角度变化来提取特征点的方法表现欠佳，提取特征点数为7个，特别是1号和3号轨迹只提取到了轨迹的开始点和结束点，不能对轨迹进行准确描述。本文利用曲线边缘检测方法的原理，提取出的特征点数为14个，在保持原轨迹精确性和子轨迹简洁性之间找到最优的平衡，表明了所提方法的合理性。

表1 三种特征点提取方法结果比较

为了比较不同方法轨迹聚类的质量，定义如下聚类质量评价公式[3]：

(12)

在时空模式下，通过计算所有聚类簇中相互轨迹段间的平方误差之和来衡量轨迹聚类质量。QMeasure越小表示聚类簇内轨迹段密度越大，聚类结果质量越高。其中dist(x,y)为聚类簇中两条轨迹段间的距离，如式(11)所示。为取得较好结果，在不同权重下分别对两种数据进行实验。图6为eps=9、minlns=30时，对飓风数据在不同权重下进行聚类所得聚类结果质量分析图。从图中可以看到，w=0.7时聚类质量达到最优，整体对权重设置具有一定的敏感性。

图6 飓风数据在不同权重下聚类质量对比

图7为eps=8、minlns=28时，对ELK93进行不同权重下聚类质量的分析比较。聚类质量在w=0.5达到最优，然而由于ELK93数据采样自1993年春季到秋季期间麋鹿的运动轨迹，时间跨度较小，故而对权重设置敏感性较低。

图7 ELK93数据在不同权重下聚类质量对比

在此，实现了轨迹聚类(TRAjectoryCLUStering,TRACLUS)算法和根据转角进行轨迹划分并由DBSCAN完成聚类的算法(简称“转角”算法)，以及本文中提出的改进算法。图8为eps=9时对大西洋飓风数据的聚类结果质量分析图，此时w为0.7。

从图8中可以看出，使用TRACLUS算法对飓风数据进行聚类，在minlns=31时达到质量最优，但由于TRACLUS在进行相似性度量时只考虑了空间特征，导致整体性能低于本文中提出算法。“转角”算法中由于根据相邻样本点变化角度来划分轨迹段结果质量低下导致QMeasure值较前两种方法偏高，为解决这种情况，可事先设定转角累加阈值，相邻样本点转角低于转角阈值时将之累加直至达到累加阈值，这时将样本点添加为特征点同时累加阈值清零，但由于需要增加参数值设置，且对结果影响较大，因此本文没有采用这种方法。使用本文算法聚类质量在minlns=30时达到最优，参数设置对聚类质量有一定的影响，但聚类质量值整体较前两种算法偏低。

图9显示了eps=8时对ELK93数据进行聚类的聚类质量图，此时w为0.5。从图中可以看出使用TRACLUS算法对ELK93数据进行聚类，聚类质量在minlns=28时达到最优，而minlns过大或过小都会对聚类质量造成较大影响。“转角”算法结果与TRACLUS类似，在minlns=28时达到最优，总体呈“倒U型”，但聚类质量低于TRACLUS。使用本文算法进行聚类，聚类质量值从minlns=25开始持续下降，在minlns=29时达到最优，因为同时考虑了空间及时间相似性，所以聚类质量总体较高。

图8 飓风数据聚类质量图(w=0.7)

图9 ELK93数据聚类质量图(w=0.5)

以ELK93 为例，同样使用文献[3]中TRACLUS算法以及本文提出改进聚类算法进行比较，比对结果如图10所示，其中(a)为使用TRACLUS算法进行聚类得到聚类簇代表轨迹，(b)为应用本文改进算法得到的聚类结果，从图中可以看出使用TRACLUS算法在只考虑空间相似性的情况下，生成聚类簇相比本文算法较大，簇内密度小。观察图10(a)最下方的一条聚类簇代表轨迹，相应本文算法将之生成为三个相对较小聚类簇，说明本文在同时度量轨迹数据时空相似性的情况下，生成聚类簇更加精细，更有使用价值。

图10 ELK93聚类结果对比

4 结语

对轨迹进行划分再聚类的方法能够很好地发现存在于复杂时空轨迹中的局部相似性，然而其聚类结果对子轨迹段划分质量具有很强的依赖性，而轨迹特征点是影响子轨迹段划分质量的关键因素， 同时相似性度量也对聚类结果具有重要影响。针对相似性度量中忽略时间特征的问题，提出了一种基于时空特征的轨迹数据聚类方法。该方法借鉴图像算法中曲线边缘信息的检测方法，通过计算轨迹上某一点与该点相邻轨迹段的变化趋势来判定该点是否为轨迹的特征点。实验表明使用该方法所提取的特征点具有较高的简洁性，并且根据特征点生成的子轨迹段集能够准确地描述轨迹结构，降低了轨迹划分对聚类质量的影响。在对子轨迹段集进行聚类的过程中，兼顾轨迹的空间与时间特征，并通过设置权重调整时空特征敏感度，实验表明基于时空模式的轨迹数据聚类方法能够发现移动对象内在结构及其动态规律。接下来的工作是进一步提高聚类效率。

)

[1]PANJ,JIANGQ,SHAOZ.Trajectoryclusteringbysamplinganddensity[J].MarineTechnologySocietyJournal, 2014, 48(6): 74-85.

[2]HUNGCC,PENGWC,LEEWC.Clusteringandaggregatingcluesoftrajectoriesforminingtrajectorypatternsandroutes[J].TheVLDBJournal, 2015, 24(2): 169-192.

[3]LEEJG,HANJ,WHANGKY.Trajectoryclustering:apartition-and-groupframework[EB/OL]. [2015- 01- 13].http://xueshu.baidu.com/s?wd=paperuri%3A%287e5e7260674abe825b7a245c93edbb10%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fciteseerx.ist.psu.edu%2Fviewdoc%2Fdownload%3Bjsessionid%3D6CE1053AAA540B0B1F600FE0C866E986%3Fdoi%3D10.1.1.76.8098%26rep%3Drep1%26type%3Dpdf&ie=utf-8&sc_us=17938122568389976672.

[4] 袁冠,夏士雄,张磊,等.基于结构相似度的轨迹聚类算法[J].通信学报,2011,32(9):103-110.(YUANG,XIASX,ZHANGL,etal.Trajectoryclusteringalgorithmbasedonstructuralsimilarity[J].JournalonCommunications, 2011, 32(9): 103-110.)

[5] 杜国红,徐克虎,杜涛.平面非规则曲线的一种快速识别与匹配算法[J].计算机工程与应用,2007,43(7):81-83.(DUGH,XUKH,DUT.Quickrecognizingandmatchingalgorithmforplanarirregularcurve[J].ComputerEngineeringandApplications, 2007, 43(7): 81-83.)

[6]CHENJ,LEUNGMK,GAOY.NoisylogorecognitionusinglinesegmentHausdorffdistance[J].PatternRecognition, 2003, 36(4): 943-955.

[7]BOLLENJ,PEPEA,MAOH.Modelingpublicmoodandemotion:Twittersentimentandsocio-economicphenomena[J].ComputerScience, 2009, 44(12): 2365-2370.

[8] 刘琴,王恺乐,饶卫雄.不等长时间序列滑窗STS距离聚类算法[J].计算机科学与探索,2015,9(11):1301-1313.(LIUQ,WANGKL,RAOWX.Non-equaltimeseriesdataclusteringalgorithmwithslidingwindowSTSdistance[J].JournalofFrontiersofComputerScienceandTechnology, 2015, 9(11): 1302-1313.)

[9] 张延玲,刘金鹏,姜保庆.移动对象子轨迹段分割与聚类算法[J].计算机工程与应用,2009,45(10):65-68.(ZHANGYL,LIUJP,JIANGBQ.Partitionandclusteringforsub-trajectoriesofmovingobjects[J].ComputerEngineeringandApplications, 2009, 45(10): 65-68.)

[10]ESTERM,KRIEGELHP,SANDERJ,etal.Adensity-basedalgorithmfordiscoveringclustersinlargespatialdatabasewithnoise[C]//Proceedingsofthe2ndInternationalConferenceonKnowledgeDiscoveryandDataMining.MenloPark:AAAIPress, 1996: 226-231.

[11] GUDMUNDSSON J, VALLADARES N. A GPU approach to subtrajectory clustering using the Fréchet distance [J]. IEEE Transactions on Parallel and Distributed Systems, 2015, 26(4): 924-937.

[12] 廖律超,蒋新华,邹复民,等.一种支持轨迹大数据潜在语义相关性挖掘的谱聚类方法[J]. 电子学报,2015,43(5):956-964.(LIAO L C, JIANG X H, ZOU F M, et al. A spectral clustering method for big trajectory data mining with latent semantic correlation [J]. Acta Electronica Sinica, 2015,43(5):956-964.)

[13] 龚玺,裴韬,孙嘉,等.时空轨迹聚类方法研究进展[J].地理科学进展,2011,30(5):522-534.(GONG X, PEI T, SUN J, et al. Review of the research progresses in trajectory clustering methods [J]. Progress in Geography, 2011, 30(5): 522-534.)

[14] ELNEKAVE S, LAST M, MAIMON O. Incremental clustering of mobile objects [C]// Proceedings of the 2007 ACM SIGMOD InternationalConference on Management of Data. New York: ACM, 2007:593-604.

[15] YUAN G, SUN P, ZHAO J, et al. A review of moving object trajectory clustering algorithms [EB/OL]. [2015- 01- 09]. https://www.researchgate.net/publication/299434359_A_review_of_moving_object_trajectory_clustering_algorithms.

This work was partially supported by Natural Science Foundation of Hebei Province (F2016202144), the Science and Technology Research Project of Colleges and Universities in Hebei Province(ZD2014030), the Tianjin Research Project of Application Foundation and Advanced Technology (14JCZD JC31600).

SHI Lukui, born in 1974, Ph. D., professor. His research interests include machine learning, data mining.

ZHANG Yanru, born in 1990, M. S. candidate. Her research interests include machine learning, data mining.

ZHANG Xin, born in 1992,M.S.candidate.Her research interests include machine learning, data mining.

Trajectory data clustering algorithm based on spatio-temporal pattern

SHI Lukui1,2*, ZHANG Yanru1, ZHANG Xin1

(1.SchoolofComputerScienceandEngineering,HebeiUniversityofTechnology,Tianjin300401,China；
2.HebeiProvinceKeyLaboratoryofBigDataCalculation(HebeiUniversityofTechnology),Tianjin300401,China)

Because the existing trajectory clustering algorithms in the similarity measurement usually used the spatial characteristics as the standards the characteristics lacking the consideration of temporal, a trajectory data clustering algorithm based on spatial-temporal pattern was proposed. The proposed algorithm was based on partition-and-group framework. Firstly, the trajectory feature points were extracted by using the curve edge detection method. Then the sub-trajectory segments were divided according to the trajectory feature points. Finally, the clustering algorithm based on density was used according to the spatio-temporal similarity between sub-trajectory segments. The experimental results show that the trajectory feature points extracted using the proposed algorithm are more accurate to describe the trajectory structure under the premise that the feature points have better simplicity. At the same time, the similarity measurement based on spatio-temporal feature obtains better clustering result by taking into account both spatial and temporal characteristics of trajectory.

spatio-temporal pattern; trajectory data; curve edge detection; similarity measurement; density based clustering

2016- 07- 21;

2016- 09- 12。

天津市应用基础与前沿技术研究计划项目(14JCZDJC31600);河北省自然科学基金专项(F2016202144 )；河北省高等学校科学技术研究项目(ZD2014030)。

石陆魁(1974—)，男，河北邯郸人，教授，博士，CCF会员，主要研究方向：机器学习、数据挖掘； 张延茹(1990—)，女，河北张家口人，硕士研究生，主要研究方向：机器学习、数据挖掘； 张欣(1992—)，女，河北衡水人，硕士研究生，主要研究方向：机器学习、数据挖掘。

1001- 9081(2017)03- 0854- 06

10.11772/j.issn.1001- 9081.2017.03.854

TP181

A