基于无监督学习卷积神经网络的振动信号模态参数识别

方 宁，周 宇，叶庆卫，李玉刚

(宁波大学 信息科学与工程学院，浙江 宁波 315211) (*通信作者电子邮箱zhouyu@nbu.edu.cn)

基于无监督学习卷积神经网络的振动信号模态参数识别

方 宁，周 宇*，叶庆卫，李玉刚

(宁波大学 信息科学与工程学院，浙江 宁波 315211) (*通信作者电子邮箱zhouyu@nbu.edu.cn)

针对现有的时域模态参数识别方法大多存在难定阶和抗噪性差的问题，提出一种无监督学习的卷积神经网络(CNN)的振动信号模态识别方法。该算法在卷积神经网络的基础上进行改进。首先，将应用于二维图像处理的卷积神经网络改成处理一维信号的卷积神经网络，其中输入层改成待提取模态参数的振动信号集合，中间层改成若干一维卷积层、抽样层，输出层得到的为信号对应的N阶模态参数集合；然后，在误差评估中，对网络计算结果(N阶模态参数集)进行振动信号重构；最后，将重构信号和输入信号之间差的平方和作为网络学习误差，使得网络变成无监督学习网络，避免模态参数提取算法的定阶难题。实验结果表明，当所构建的卷积神经网络应用于模态参数提取时，与随机子空间识别(SSI)算法及其局部线性嵌入(LLE)算法对比，在噪声干扰下，构建的卷积神经网络识别精度要高于SSI算法与LLE算法，具有抗噪声强、避免了定阶难题的优点。

卷积神经网络；模态参数；无监督学习；学习误差；随机子空间识别；局部线性嵌入

0 引言

振动信号的模态参数识别是大型结构健康监测和结构损伤探测领域振动检测技术的核心，日益成为一种有效而实用的故障诊断和安全检测方法。目前工程中常用的环境激励下模态参数识别方法[1-4]有时域法(依式时域法(Ibrahim Time Domain, ITD)、随机子空间识别(Stochastic Subspace Identification, SSI)算法、稀疏时域法(Spare Time Domain, STD)、随机减量法等)、频域法(最小二乘圆拟合法、Levy法、正交多项式拟合法等)和时频分析法。现存的一些时域方法也存在着一定的缺点, 比如在实测响应信号中常常包含噪声,所识别的模态中除了系统模态外,还包含噪声模态。如何甄别和剔除噪声模态,以及合理的模型定阶等问题,一直是时域法研究中的重要课题。随着各种现代信号处理技术的不断涌现,为研究结构模态参数识别提供了新的思路[5]。如文献[6]以流行学习为理论，从提取结构的几何或固有特征出发，以系统结构的响应数据为分析对象，提出一种利用局部线性嵌入(Locally Linear Embedding, LLE)的模态识别方法。

国内外的许多研究表明,现代信号处理技术如人工神经网络能够应用到环境激励下的结构参数识别中,文献[7]提出的基于线性神经网络的自回归滑动平均模型(Auto-Regressive and Moving Average Model, ARMA)提取模态参数方法,具有很强的抗噪性，并且具有很高识别精度, 但线性神经网络在确定网络输出权重时存在稳态失调误差和收敛速度相矛盾的问题；文献[8]提出BP神经网络非参数化模型代替ARMA模型的参数化模型来进行结构物理参数抽取,但BP神经网络存在学习速度慢、易陷入极值等问题；文献[9]提出的基于连续小波变换和反向传播神经网络的模态参数辨识方法,在信号的采样时间很短的时候也能够准确识别各阶模态，实用性较强，并体现出一定的抗噪能力。由于在信号幅度的突变处延拓信号的质量较差给阻尼比的估计带来一定影响。从提取模态参数消耗的时间来看,信噪比越低，训练神经网络所需要的时间越长。

卷积神经网络(Convolutional Neural Network, CNN)是人工神经网络的一种，已成为当前语音分析[10]和图像识别领域[11-12]的热点。卷积神经网络已广泛应用于特征学习中。如谢智歌等[13]提出基于卷积-自动编码机的三维形状特征学习，根据卷积神经网络与自动编码机的两者结合，结合两者的优点，具有训练速度快、表达能力强等良好性质，自动编码机是一种无监督的神经网络，但是自动编码机的神经元可以有效地可视化，在加上卷积特征映射阶段之后，神经元的可视化方法并没有那么直接。

为了解决自动编码机与卷积神经网络过程中的结构复杂的问题，本文提出无监督学习卷积神经网络的模态参数提取方法。在原有卷积神经网络的基础上，将输入改为一维振动信号的网络，通过多核卷积运算把一维的时序信号映射到合适的高维空间，有效地去分离信号模态特征、去除时间相关性；并且为了避免模态参数定阶，在训练网络过程中将反向传播的误差改为计算输出模态参数重构相加得到的复原信号与输入信号之间的误差，使构建的卷积神经网络为无监督学习的网络，并同传统的时域方法SSI和流行学习的LLE算法进行了实验对比。

1 经典卷积神经网络

CNN是一种结构简单的多层感知器，是一种为图像处理而特别设计的一种人工神经网络，卷积神经网网络的结构不同于其他网络的两大突出特点：稀疏连接和权重共享。稀疏连接和共享权重带来的直接好处是减少网络各层之间的连接，降低网络复杂度，同时又降低了过拟合的风险，主要应用于特征提取和识别研究[14-15]。网络由输入层、卷积层、采样层和输出层组成。如图1所示。

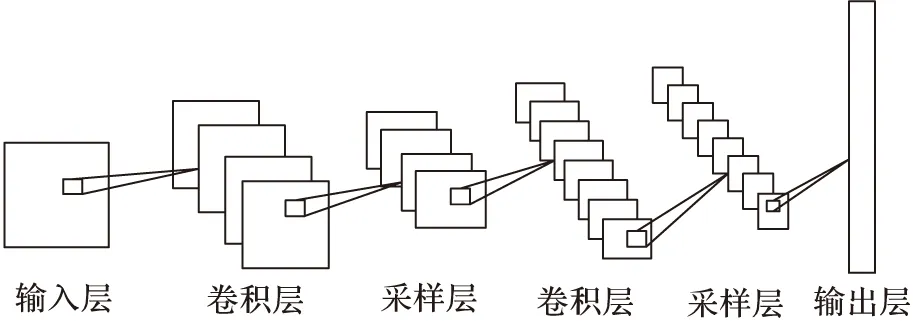
图1 卷积神经网络结构

卷积神经网络权重更新执行的是导师训练学习方法，网络的学习过程包含前向传播阶段和后向传播过程，卷积神经网络的训练过程[16]如下。

1.1 前向传播阶段

1)卷积层的前向传播。

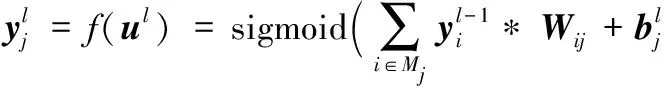
(1)

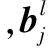
2)采样层的前向传播。

(2)

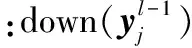
1.2 反向传播阶段

通过计算前向传播阶段得到的实际输出O与理想的输出Y之间的平均误差代价函数E，通过反向传播误差进行修正权重和偏置，分为三个步骤：反向传播求残差、梯度计算和修正权重和偏置过程，修正权重和偏置的公式：

(3)

其中：w为现有权重，w′为修正后的权重，b为现有偏置，b′为修正后的偏置。

1)卷积层的反向传播。卷积层的残差计算公式为：

(4)

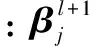
(5)

卷积层梯度计算：

(6)

2)采样层的反向传播。采样层的残差计算公式为：

(7)

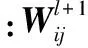
采样层梯度计算：

(8)

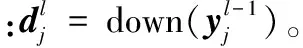
3)输出层的残差计算公式：

(9)

其中：tL为理想输出，yL为全连接得到实际输出，将输出层部的残差δL通过式(7)传递到采样层，再将采样层的残差经过式(4)得到卷积层的残差，依次进行反向传递。将式(6)和(8)代入到式(3)中进行权重和偏置的修正。

2 无监督学习卷积神经网络的构建

一般粘性阻尼系统的多模态振动信号模型表达式为：

(10)

其中：gk(t)为单模态信号，单模态信号的表达式为：gk(t)=ake-λktcos(ωkt+φk);M为模态个数。(ak,λk,ωk,φk)为第k阶模态参数，其中ak为振型系数，λk为衰减系数，ωk为主频率，φk为初始相位。

对有阻尼结果的自由衰减振动才成立，为了提取式(10)中的各阶模态参数{(a1,λ1,ω1,φ1),(a2,λ2,ω2,φ2),…,(aM,λM,ωM,φM)}，使用卷积神经网络改进算法，如图2所示为无监督学习卷积神经网络结构。

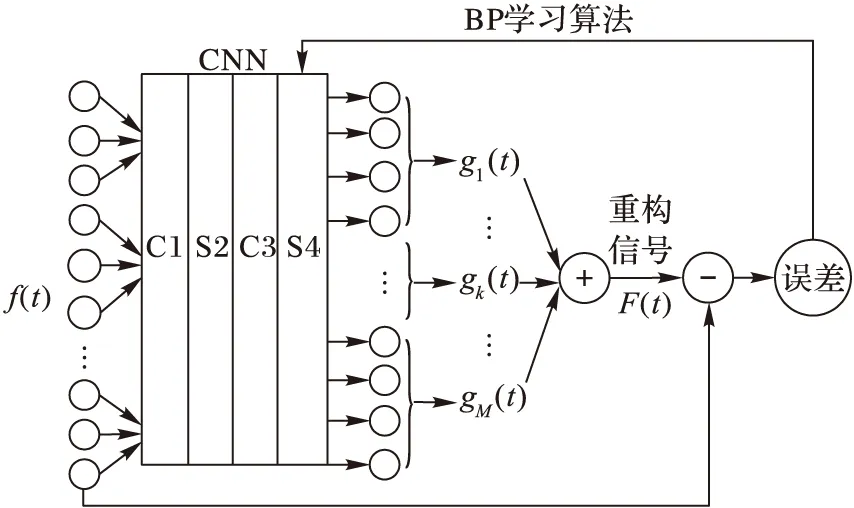
图2 无监督学习卷积神经网络结构

2.1 改进卷积神经网络的前向传播过程

将原输入为二维信号的网络改成输入为一维振动信号f(t)，经过CNN中的卷积层C1,C3和采样层S2,S4后得到的输出为各阶模态参数。如图3为一维信号的卷积神经网络前向传播过程。

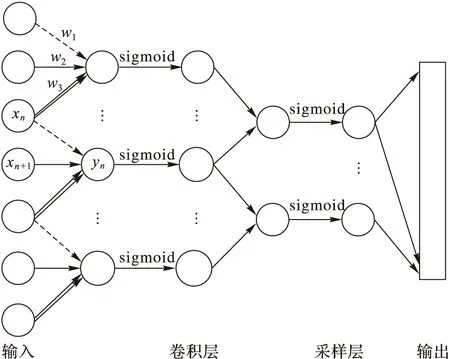
图3 一维信号的卷积神经网络前向传播过程

改进后CNN网络卷积层和采样层的前向传播过程如下。

卷积层输出为：

(11)

使用均值采样，采样层输出为：

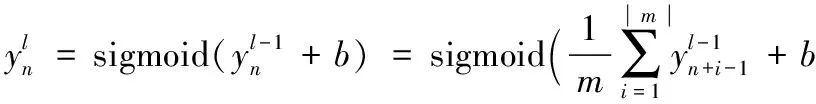
(12)

2.2 改进卷积神经网络的反向传播过程

用各阶模态参数通过单模态振动信号公式重构各阶单模态振动信号，分别为g1(t),g2(t),…,gM(t),表达式为：

(13)

其中：k=1,2，…,M。将重构的单模态振动信号gk(t)相加得到复原振动信号F(t)为：

(14)

通过计算复原信号F(t)与输入振动信号f(t)之间的误差，通过BP学习算法进行反向传播误差不断调整权值。

根据现有网络卷积层的残差计算式(4)可得到一维振动信号的神经网络的残差计算公式为：

(15)

卷积层梯度计算：

(16)

根据式(7)可以得到一维信号的网络采样层的残差为:

(17)

采样层梯度计算公式为：

(18)

输出层误差为：

(19)

其中B为信号采样点的集合。输出层的残差公式为：

(20)

改进的卷积神经网络提取振动信号模态参数具体流程如图4所示。

图4 改进的卷积神经网络提取模态参数流程

3 实验验证

3.1 实验数据集

在实验中使用Matlab作为仿真工具进行计算，实际振动信号使用多模态振动信号，因此在仿真过程中使用多模态振动信号进行训练和测试。根据式(10)表达式，在a=-1:0.1:2,λ=0.1:-0.001:0.001,ω=1:0.1:6,φ=0:0.05:0.5中分别自由选取组合的多模态振动信号中随机选取1 250条，其中1 000条作为训练集T1，另外250条作为测试集T2。实际振动信号测量过程中的实验仪器的频率一般为50Hz,所以仿真过程中对振动信号的采样频率选为100Hz。

3.2 实验结果与分析

假设测试集T2中的一个三模态仿真信号x0(t)，其具有较低的频率成分，与大桥斜拉索频率接近，仿真信号为:

x0(t)=0.5e-0.012tcos(1.8t+0.25)+ 1.2e-0.019tcos(1.4t+0.1)- 0.6e-0.025tcos(2.6t+0.05)

(21)

由理论计算得到该振动信号的固有频率分别为w1=0.287，w2=0.223，w3=0.414；阻尼比分别为ξ1=0.041 8,ξ2=0.085 2 ,ξ3=0.060 4；模态振型分别为Ω1=0.5，Ω2=1.2，Ω3=-0.6。

根据表1可以得到结论：一维振动信号的改进卷积神经网络能准确提取振动信号的模态参数，识别精度较高。在实际信号的采集和测量过程中振动信号会出现噪声的干扰，所以为了验证本文提出的算法的实际意义，在下面仿真实验中，讨论噪声强度和网络迭代次数的取值对一维卷积神经网络提取精度的影响。

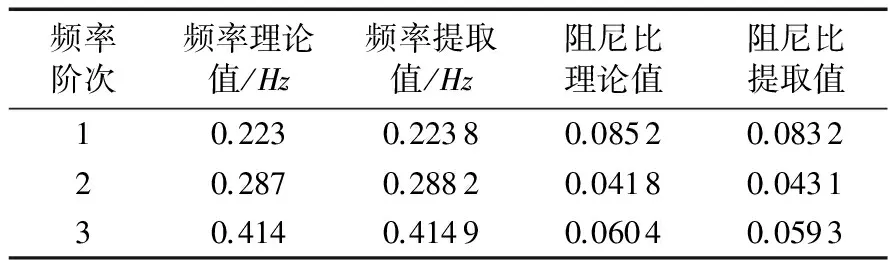
表1 本文算法模态识别结果

3.2.1 噪声强度对频率提取的影响

在测试卷积神经网络的过程中测试集由振动信号加上白噪声组成，选取迭代次数10，训练集为1 000的网络进行实验。实验结果如图5所示，在图中可以看到信噪比(Signal-to-NoiseRatio,SNR)在0～50dB变化，随着SNR的变化，频率平均相对误差基本上都在0.6%附近变化。根据实验结果可以得出结论：频率的平均相对误差基本不随着噪声强度的变化而变化，所以卷积神经网络的抗噪性强，提取出的模态参数准确，受噪声的影响小。

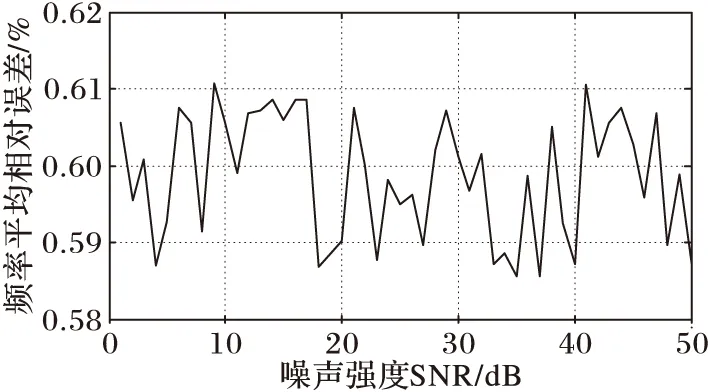
图5 频率平均相对误差与噪声强度SNR的关系

3.2.2 迭代次数对频率提取的影响

在卷积神经网络的训练过程中，实验结果会受迭代次数的影响，所以为了保证数据的准确性，选取训练集为1 000，噪声强度SNR=20的网络进行实验。实验结果如图6所示，通过图可以看出频率误差随着迭代次数的增加而减小，在迭代次数为10次的时候频率误差达到稳定值，在迭代次数较小的情况下，频率误差幅度较大，此时数据的随机性比较大，所以在训练卷积神经网络的过程中，要综合训练速度和准确率来选择合适的迭代次数。

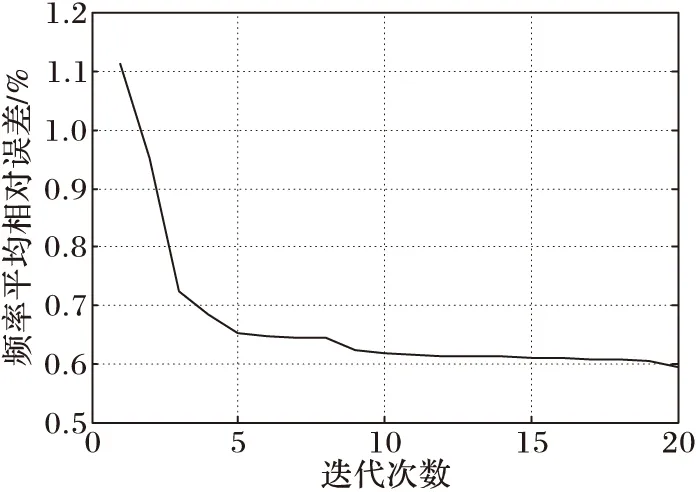
图6 频率平均相对误差与迭代次数N的关系

综合上述实验结果，可以得出结论：训练出的卷积神经网络除了保证提取模态参数的准确性，另一方面还要保证训练速度，要选择合适的迭代次数才能得到稳定的网络，这就是本文的关键。

3.2.3 与时域识别算法对比分析

将通过不断训练得到的一维信号的卷积神经网络提取模态参数法与环境振动模态参数时域识别方法中的随机子空间法(SSI)与局部线性嵌入(LLE)算法进行对比。结果如图7所示。

由图7可以看出：SSI算法识别频率的精度随着信噪比的增加而增加，SSI算法在信噪比在16 dB时识别频率的精度跟卷积神经网络方法识别的精度差不多，SSI方法表现出来的是对噪声敏感；同时LLE算法在噪声干扰大的时候提取精度低于本文算法；而相反的是卷积神经网络法识别的频率平均相对误差一直保持稳定值，表现出很强的抗噪性，识别精度受噪声干扰小。

3.3 实例应用

用本文算法对实际采集的振动信号进行模态参数提取，工程数据来自宁波斜拉索大桥，如图8。大桥全长67 m,由102根直径0.15 m拉索构成支撑系统；用WS-ZHT2振动设备及双传感器采集振动信号，双传感器安装在拉索和梁端的铰支部位，能有效感应索-梁耦合的拉索振动。

图7 卷积神经网络方法与SSI和LLE方法对比

图8 斜拉索大桥

根据振动设备及传感器采集的振动信号，取其中一条，波形图如图9所示，可看到采集的振动信号受噪声干扰。使用本文算法和时域法中的随机子空间识别法(SSI)、局部线性嵌入算法(LLE)分别对其进行模态参数提取。使用本文算法的实验参数设为振动信号采样频率为100 Hz，训练数为1 000的训练集，网络迭代次数为10次，通过训练网络，测试集得到的实验结果与环境振动模态参数时域识别方法中的随机子空间识别法(SSI)和LLE算法进行比较。

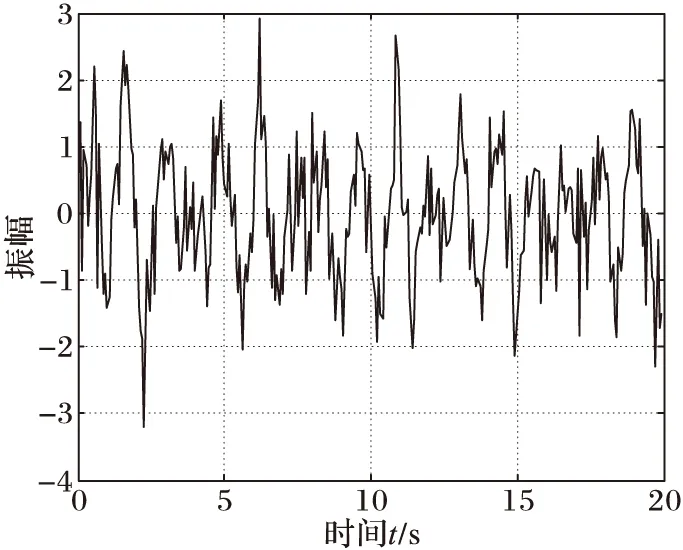
图9 斜拉索大桥振动信号

由表2三种方法的模态识别结果可以看出本文算法的结果要更加接近于频率理论值(大桥管理服务有限公司提供)，提取的精度要高于SSI和LLE算法。SSI和LLE受噪声的影响比较大，且SSI算法和LLE算法识别模态的时候需要定阶、消噪处理，在实际信号处理过程中比较困难，由于卷积神经网络是非线性映射，对噪声不太敏感，所以提取过程稍微简单，识别精度也高于SSI和LLE算法，在斜拉索的监测过程中进一步验证了无监督学习卷积神经网络的抗噪性。

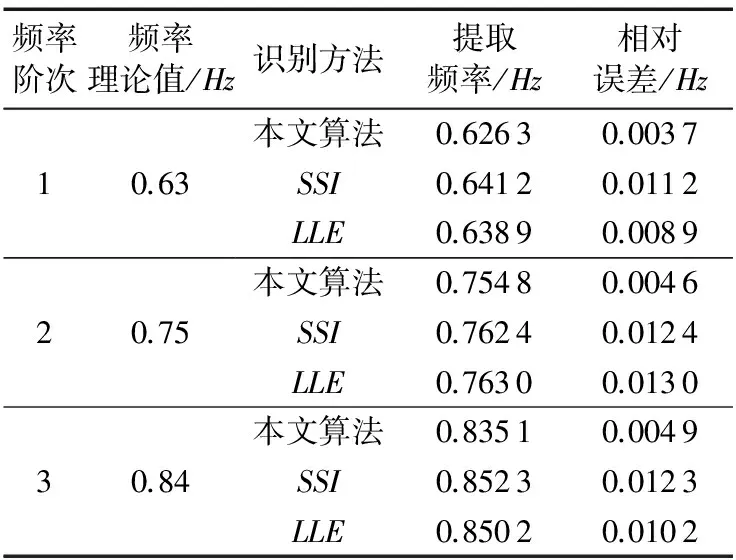
表2 三种方法模态参数识别结果对比

4 结语

本文算法在卷积神经网络的基础上，将原用于图像处理的神经网络改为处理一维信号的结构，在输出层引入无监督思想，不需要指定教师信号，避免模态参数提取算法中的定阶难题。将该算法用于实际斜拉索大桥桥梁振动信号的模态参数提取，将其与SSI和LLE进行对比实验。实验结果表明，本文算法具有更好的抗噪性和识别精度。针对卷积神经网络的BP方向学习存在易陷入极值的问题，使用粒子群算法进行寻优，以提高识别精度，是下一步需要深入的问题。

References)

[1] 曹树谦，张文德，萧龙翔.振动结构模态分析理论、实验与应用[M].天津:天津大学出版社,2001：152-156.(CAO S Q, ZHANG W D, XIAO L X. The Theory, Experiment and Application of Structure Vibration Modal Analysis [M]. Tianjin: Tianjin University Press, 2001: 152-156.)

[2] 续秀忠,华宏星,陈兆能.基于环境激励的模态参数辨识方法综述[J].振动与冲击,2002,21(3):1-5.(XU X Z, HUA H X, CHEN Z N. Review of modal identification method based on ambient excitation [J]. Journal of Vibration and Shock, 2002, 21(3): 1-5.)

[3] 秦世强,蒲黔辉,施洲.环境激励下大型桥梁模态参数识别的一种方法[J].振动与冲击,2012,31(2):95-100.(QIN S Q, PU Q H, SHI Z. A method of modal parameters identification using ambient vibration measurements for a large-scale bridge [J]. Journal of Vibration and Shock, 2012, 31(2): 95-100.)

[4] 单德山,李乔.桥梁结构模态参数的时频域识别[J].桥梁建设,2015,31(2):26-31.(SHAN D S, LI Q, Model parameters of bridge structure in time-frequency domain [J]. Bridge Construction, 2015, 31(2): 26-31.)

[5] 付志超,程伟,李晶,等.一种基于神经网络的模态参数识别方法[J].机械强度,2010,32(6):899-904.(FU Z C,CHENG W,LI J,et al.Model parameters identification via an ANN-based method [J]. Journal of Mechanical Strength, 2010, 32(6):899-904.)

[6] 白俊卿,闫桂荣,王成.利用局部线性嵌入的模态识别[J].西安交通大学学报,2013,47(1):85-89.(BAI J Q, YAN G R, WANG C. Modal identification method following locally linear embedding [J]. Journal of Xi’an Jiaotong University, 2013, 47(1): 85-89.

[7] 孙宗光,高赞明,倪一清.基于神经网络的损伤构件及损伤程度识别[J].工程力学,2006,23(2):18-22.(SUN Z G, GAO Z M, NI Y Q. Identification of damaged members and damage extent in bridge deck by neural network [J]. Engineering Mechanics, 2006, 23(2): 18-22.)[8] 许斌,龚安苏,贺佳,等.基于神经网络模型的结构参数提取新方法[J].工程力学,2011,28(4):35-41.(XU B, GONG A S, HE J, et al. A novel structural parameter extraction with neural network based nonparametric model [J]. Engineering Mechanics, 2011, 28(4): 35-41.)

[9] 代煜,张建勋.基于小波变换和反向传播网络的模态参数辨识[J].振动与冲击,2012,31(3):55-59.(DAI Y, ZHANG J X. Identification of modal parameters based on wavelet transform and back propagation network [J]. Journal of Vibration and Shock, 2012, 31(3): 55-59.)

[10] 张晴晴,刘勇,潘接林,等.基于卷积神经网络的连续语音识别[J].工程科学学报,2015,37(9):1212-1217.(ZHANG Q Q, LIU Y, PAN J L, et al. Continuous speech recognition by convolutional neural networks [J]. Journal of University of Science and Technology Beijing, 2015, 37(9): 1212-1217.)

[11] DRUKI A A, SPITSYN V G. Development of sequential optimizational algorithms for object detection in images [C]// Proceedings of the 2015 International Siberian Conference on Control and Communications. Piscataway, NJ: IEEE, 2015: 21-23.

[12] 徐姗姗,刘应安,徐昇.基于卷积神经网络的木材缺陷识别[J].山东大学学报(工学版),2013,43(2):23-28.(XU S S, LIU Y A, XU S. Wood defects recognition based on the convolutional neural network [J]. Journal of Shandong University (Engineering Science), 2013, 43(2): 23-28.)

[13] 谢智歌,王岳青,窦勇,等.基于卷积-自动编码机的三维形状特征学习[J].计算机辅助设计与图形学学报,2015,27(11):2058-2064.(XIE Z G, WANG Y Q, DOU Y, et al. 3D feature learning via convolutional auto-encoder extreme learning machine [J]. Journal of Computer-Aided Design and Computer Graphics, 2015, 27(11): 2058-2064.)

[14] ABDEL-HAMID O, MOHAMED A, JIANG H, et al. Convolutional neural networks for speech recognition [J]. IEEE Transactions on Audio, Speech and Language Processing, 2014, 22(1): 1533-1545.

[15] SWIETOJANSKI P，GHOSHAL A，RENALS S. Convolutional neural networks for distant speech recognition [J]. IEEE Signal Processing Letters, 2014, 21(9): 1120-1124.

[16] BOUVRIE J. Notes on convolutional neural networks . 〖2016- 01- 25〗. https://core.ac.uk/download/pdf/86960.pdf.

This work is partially supported by the National Natural Sciences Foundation of China (61071198), the Natural Science Foundation of Zhejiang Province (LY13F010015 ), the Science and Technology Innovation Team of Zhejiang Province (2013TD21), the Scientific Research Foundation of Ningbo University (xkx11417).

FANG Ning, born in 1992, M. S. candidate. Her research interests include vibration signal processing ,deep learning.

ZHOU Yu, born in 1960, M. S., professor. His research interests include vibration signal processing, network communications, information security.

YE Qingwei, born in 1970, Ph. D., associate professor. His research interests include vibration signal processing, intelligent optimization.

LI Yugang, born in 1991, M. S. candidate. His research interests include vibration signal processing.

Modal parameter identification of vibration signal based on unsupervised learning convolutional neural network

FANG Ning, ZHOU Yu*, YE Qingwei, LI Yugang

(CollegeofInformationScienceandEngineering,NingboUniversity,NingboZhejiang315211,China)

Aiming at the problem that most of the existing time-domain modal parameter identification methods are difficult to set order and resist noise poorly, an unsupervised learning Convolution Neural Network (CNN) method for vibration signal modal identification was proposed. The proposed algorithm was improved on the basis of CNN. Firstly, the CNN applied to two-dimensional image processing was changed into the CNN to deal with one-dimensional signal. The input layer was changed into the vibration signal set of modal parameters to be extracted, and the intermediate layer was changed into several one-dimensional convolution layers, sampled layers, and output layer was the set ofN-order modal parameters corresponding to the signal. Then, in the error evaluation, the network calculation result (N-order modal parameter set) was reconstructed by the vibration signals. Finally, the squared sum of the difference between the reconstructed signal and the input signal was taken as the network learning error, which makes the network become an unsupervised learning network, and avoids the ordering problem of modal parameter extraction algorithm. The experimental results show that when the constructed CNN is applied to modal parameter extraction, compared with the Stochastic Subspace Identification (SSI) algorithm and its Local Linear Embedding (LLE) algorithm, the convolutional neural network identification accuracy is higher than that of the SSI algorithm and the LLE algorithm under noise interference. It has strong noise resistance and avoids the ordering problem.

Convolutional Neural Network (CNN); modal parameter; unsupervised learning; learning error; Stochastic Subspace Identification (SSI); Locally Linear Embedding (LLE)

2016- 08- 19;

2016- 10- 29。

国家自然科学基金资助项目(61071198)；浙江省自然科学基金资助项目(LY13F010015)；浙江省科技创新团队资助项目(2013TD21); 宁波大学科研基金(学科项目)资助项目(xkx11417)。

方宁(1992—),女,湖北黄冈人,硕士研究生,主要研究方向:振动信号处理、深度学习; 周宇(1960—),男,山东威海人,教授,硕士,主要研究方向:振动信号处理、网络多媒体通信、信息安全; 叶庆卫(1970—),男,浙江衢州人,副教授,博士,主要研究方向:振动信号处理、智能优化; 李玉刚(1991—),男,安徽合肥人,硕士研究生,主要研究方向:振动信号处理。

1001- 9081(2017)03- 0786- 05

10.11772/j.issn.1001- 9081.2017.03.786

TP

A